D. H. Lumb1 - J. G. Bartlett2,3 - A. K. Romer4,9 - A. Blanchard5 - D. J. Burke6 - C. A. Collins7 - R. C. Nichol4 - M. Giard8 - P. B. Marty5 - J. Nevalainen6 - R. Sadat5 - S. C. Vauclair5
1 - Science Payloads and Advanced Concepts Office, European Space Agency, ESTEC, 2200AG Noordwijk, The Netherlands
2 -
APC - Université Paris 7/PCC - Collège de France, 11 Pl. Marcelin Berthelot,
75231 Paris Cedex 05, France
3 -
Centre de Données astronomiques de Strasbourg, 11 rue de
l'Université, 67000 Strasbourg, France
4 -
Physics Department, Carnegie Mellon University, Pittsburgh, PA 15213,
USA
5 -
Laboratoire d'Astrophysique, OMP, CNRS, UPS, 14 Av. Ed. Belin, 31400 Toulouse, France
6 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
7 -
Astrophysics Research Institute, Liverpool John Moores University, Twelve Quays House, Egerton Wharf, Birkenhead CH41 1LD, UK
8 -
Centre d'Étude Spatiale des Rayonnements, 9 avenue du Colonel Roche, BP 4346, 31028 Toulouse, France
9 -
Astronomy Centre, Dept. of Physics and Astronomy, University of Sussex, Brighton, UK
Received 14 November 2003 / Accepted 17 March 2004
Abstract
We describe XMM-Newton Guaranteed Time observations of a
sample of eight high redshift
(0.45<z<0.62) clusters. The goal of
these observations was to measure the luminosity and the temperature of
the clusters to a precision of ![]() 10%, leading to constraints on the
possible evolution of the luminosity-temperature (
Lx-Tx) relation, and ultimately on the values of the matter density,
10%, leading to constraints on the
possible evolution of the luminosity-temperature (
Lx-Tx) relation, and ultimately on the values of the matter density,
![]() ,
and, to a lesser extent, the cosmological constant
,
and, to a lesser extent, the cosmological constant
![]() .
The
clusters were drawn from the SHARC and 160 Square Degree (160SD) ROSAT
surveys and span a bolometric (0.0-20 keV) luminosity range of 2.0 to
.
The
clusters were drawn from the SHARC and 160 Square Degree (160SD) ROSAT
surveys and span a bolometric (0.0-20 keV) luminosity range of 2.0 to
![]() erg s-1 (H0=50,
erg s-1 (H0=50,
![]() ,
,
![]() ). Here we describe our data analysis
techniques and present, for the first time with XMM-Newton, a
Lx-Tx relation. For each of
the eight clusters in the sample, we have measured total
(
). Here we describe our data analysis
techniques and present, for the first time with XMM-Newton, a
Lx-Tx relation. For each of
the eight clusters in the sample, we have measured total
(
![]() )
bolometric luminosities, performed
)
bolometric luminosities, performed ![]() -model fits
to the radial surface profiles and made spectral fits to a single
temperature isothermal model. We describe data analysis techniques
that pay particular attention to background mitigation. We have also estimated temperatures and
luminosities for two known clusters (Abell 2246 and RX J1325.0-3814),
and one new high redshift cluster candidate (XMMU J084701.8+345117),
that were detected off-axis. Characterizing the
Lx-Txrelation as
-model fits
to the radial surface profiles and made spectral fits to a single
temperature isothermal model. We describe data analysis techniques
that pay particular attention to background mitigation. We have also estimated temperatures and
luminosities for two known clusters (Abell 2246 and RX J1325.0-3814),
and one new high redshift cluster candidate (XMMU J084701.8+345117),
that were detected off-axis. Characterizing the
Lx-Txrelation as
![]() ,
we find
,
we find
![]() erg s-1 and
erg s-1 and
![]() for an
for an
![]() ,
H0=50 km s-1 Mpc-1 cosmology
at a typical redshift
,
H0=50 km s-1 Mpc-1 cosmology
at a typical redshift
![]() .
Comparing with the low
redshift study by Markevitch (1998), we find
.
Comparing with the low
redshift study by Markevitch (1998), we find ![]() to be in agreement, and assuming
Lx-Txto evolve as
(1+z)A , we find
to be in agreement, and assuming
Lx-Txto evolve as
(1+z)A , we find
![]() for the same cosmology and
A=1.52+0.26-0.27 for an
for the same cosmology and
A=1.52+0.26-0.27 for an
![]() cosmology. Our A values are very similar to
those found previously by Vikhlinin et al. (2002) using a compilation of
Chandra observations of
0.39<z<1.26 clusters. We conclude that
there is now evidence from both XMM-Newton and Chandra for an
evolutionary trend in the
Lx-Tx relation. This
evolution is significantly below the level expected from the
predictions of the self-similar model for an
cosmology. Our A values are very similar to
those found previously by Vikhlinin et al. (2002) using a compilation of
Chandra observations of
0.39<z<1.26 clusters. We conclude that
there is now evidence from both XMM-Newton and Chandra for an
evolutionary trend in the
Lx-Tx relation. This
evolution is significantly below the level expected from the
predictions of the self-similar model for an
![]() ,
cosmology, but consistent with self-similar model in an
,
cosmology, but consistent with self-similar model in an
![]() cosmology.
Our observations lend support
to the robustness and completeness of the SHARC and 160SD surveys.
cosmology.
Our observations lend support
to the robustness and completeness of the SHARC and 160SD surveys.
Key words: X-rays: galaxies: clusters
As the most massive gravitationally bound objects in the universe, galaxy clusters are particularly sensitive to the evolution of the density perturbations responsible for their formation. Cluster abundance as a function of mass and redshift is dictated by the mass function (Press & Schechter 1974; Jenkins et al. 2001), which gives the comoving space density of collapsed objects as a function of mass and redshift. In standard models, the mass function falls off as a Gaussian at the high mass end, reflecting the Gaussian nature of the density perturbations. Galaxy cluster abundance is therefore exquistely sensitive to the amplitude of the perturbations and its evolution. Since this evolution is controlled by the underlying cosmological background, observations of cluster abundance offer an effective way to constrain certain cosmological parameters, such as the density parameter (Oukbir & Blanchard 1992; Blanchard & Bartlett 1998) or the dark energy parameter and equation-of-state (Majumdar & Mohr 2003; Wang & Steinhardt 1998). The present day cluster abundance is degenerate in the matter density and amplitude of the power spectrum; evolution of the abundance breaks this degeneracy. Constraints obtained in this manner are complementary to others that essentially rely on determinations of cosmological distances; for example, those found by observations of supernovae type Ia or by measurements of cosmic microwave background anisotropies.
Cluster mass is, however, difficult to measure directly, and in practice one seeks a direct observable that is closely related to virial mass. Lensing surveys would seem the most suited to the task, as the effects of lensing are of course directly related to mass (albeit projected along the line-of-sight). However, cluster mass estimates from weak and strong lensing remain controversial as they suffer from several systematic uncertainties (e.g. projection effects). Among X-ray observables, intracluster gas temperature is expected to be tightly correlated with virial mass, an expectation borne out by simple hydrostatic considerations as well as by numerical simulations (Evrard et al. 1996; Bryan & Norman 1998). X-ray luminosity, on the other hand, is a much less robust mass indicator, despite being significantly easier to measure, because it depends on the density profile of the intracluster gas, the physics of which is currently difficult to model.
With a calibrated Tx-M (temperature-mass) relation, the mass
function can be translated into an observable cluster temperature
distribution function
![]() .
The exact T-M relation to use is of
course a key ingredient, one that may be addressed, for example, using
numerical simulations, or directly from detailed observations that
determine both cluster mass and temperature (e.g. Nevalainen et al. 2000).
Figure 1 compares temperature function predictions for a
high matter density and a flat model, both normalized to the
present-day, observed
.
The exact T-M relation to use is of
course a key ingredient, one that may be addressed, for example, using
numerical simulations, or directly from detailed observations that
determine both cluster mass and temperature (e.g. Nevalainen et al. 2000).
Figure 1 compares temperature function predictions for a
high matter density and a flat model, both normalized to the
present-day, observed
![]() (e.g. Henry & Arnaud 1991;
Edge et al. 1990; Blanchard et al. 2000; Ikebe et al. 2002).
Evolution toward higher redshift is strikingly different in two
cosmological models differing by their matter content alone and illustrating
the above argument.
(e.g. Henry & Arnaud 1991;
Edge et al. 1990; Blanchard et al. 2000; Ikebe et al. 2002).
Evolution toward higher redshift is strikingly different in two
cosmological models differing by their matter content alone and illustrating
the above argument.
Despite this obvious promise, it has been difficult to use
![]() to explore the cosmological model because direct measurements of
Tx at z>0 require long integration with satellite
observations. Prior to the launch of Chandra and XMM-Newton, the
number of measured cluster temperatures at high redshifts was very
small. This is attested to by the fact that the most distant
determination of
to explore the cosmological model because direct measurements of
Tx at z>0 require long integration with satellite
observations. Prior to the launch of Chandra and XMM-Newton, the
number of measured cluster temperatures at high redshifts was very
small. This is attested to by the fact that the most distant
determination of
![]() (Henry 2000) to date was based on a sample of
only fourteen z>0.3 clusters (mean
(Henry 2000) to date was based on a sample of
only fourteen z>0.3 clusters (mean ![]() 0.38) from the Einstein Medium Sensitivity
Survey (EMSS;
Gioia et al. 1990).
0.38) from the Einstein Medium Sensitivity
Survey (EMSS;
Gioia et al. 1990).
An alternative, but related approach is to apply a luminosity-temperature ( Lx-Tx) relation to a flux-limited sample, thereby obtaining either the temperature function, or a redshift distribution at given temperature (Oukbir & Blanchard 1997; Sadat et al. 1998; Reichart et al. 1999; Borgani et al. 1999; Borgani et al. 2001). The advantage of this approach is that it does not require detailed X-ray spectroscopy of all the clusters in a flux-limited sample to establish the Lx-Tx relation and its evolution. There are now several flux limited catalogs of medium to high redshift clusters, in addition to the EMSS, to which one can apply this technique. These include those based on data from the ROSAT All Sky Survey (e.g. Ebeling et al. 2001; Zhang et al. 2003), NEP (e.g. Gioia et al. 2001; Henry et al. 2001); and from the ROSAT pointing archive (e.g. Romer et al. 2000; Burke et al. 2003; Vikhlinin et al. 1998; Mullis et al. 2003; Scharf et al. 1997; Rosati et al. 1995).
| Cluster ID | RA | Dec | z | Date | Obs ID | Duration | Filter |
| RX J0337.7-2522 | 03:37:45 | -25:22:26 | 0.577s | 2001-08-18 T11:46:53 | 0107860401 | 58 942 | MEDIUM |
| RX J0505.3-2849 | 05:05:20 | -28:49:05 | 0.509s | 2001-09-01 T13:17:36 | 0111160201 | 48 867 | THIN |
| RX J0847.2+3449 | 08:47:11 | +34:49:16 | 0.560v | 2001-10-07 T11:55:10 | 0107860501 | 81 143 | THIN |
| RX J1120.1+4318 | 11:20:07 | +43:18:05 | 0.600b | 2001-05-08 T20:50:37 | 0107860201 | 22 627 | THIN |
| RX J1325.5-3826 | 13:25:20 | -38:24:55 | 0.445s | 2002-01-19 T02:30:04 | 0110890101 | 60 894 | MEDIUM |
| RX J1334.3+5030 | 13:34:20 | +50:30:54 | 0.620b | 2001-06-07 T20:19:43 | 0111160101 | 47 614 | THIN |
| RX J1354.2-0222 | 13:54:17 | -02:21:46 | 0.551s | 2002-07-19 T15:16:53 | 0112250101 | 33 374 | THIN |
| RX J1701.3+6414 | 17:01:23 | +64:14:08 | 0.453b | 2002-05-31 T17:49:42 | 0107860301 | 18 172 | MEDIUM |
The data were processed through the XMM-Newton Science Analysis Sub-System (SAS; Watson et al. 2001) version 5.3, in order to register photons from detector to sky co-ordinates, to correct energy data for gain and charge transfer losses, and remove instrument noise artifacts. This provided calibrated event lists as a starting point for our detailed data reduction.
Part of the XMM-Newton orbit lies within the magnetosphere, and
consequently the spacecraft can encounter clouds of protons
accelerated by magnetic reconnection. When these particles scatter
through the mirror system they are concentrated onto the focal plane,
and an enhanced background rate can occur. These intervals were
identified by forming histograms of events with energy ![]() 10 keV,
located in single pixels, in time bins of 50 (100) s in the PN
(MOS) camera(s). Due to variations in the baseline raw cosmic ray rate
experienced through the mission to date (probably due to modulation by
the solar activity and/or the seasonal variation of satellite apogee
direction), we prefer not filter at fixed background count rates, rather
for each exposure we define
10 keV,
located in single pixels, in time bins of 50 (100) s in the PN
(MOS) camera(s). Due to variations in the baseline raw cosmic ray rate
experienced through the mission to date (probably due to modulation by
the solar activity and/or the seasonal variation of satellite apogee
direction), we prefer not filter at fixed background count rates, rather
for each exposure we define
![]() limits after ignoring the
highest count rate periods (Figs. 2 and 3). Table 2 summarizes the total on-axis
Good Time Interval (GTI) exposure times extracted for each
observation using this procedure.
limits after ignoring the
highest count rate periods (Figs. 2 and 3). Table 2 summarizes the total on-axis
Good Time Interval (GTI) exposure times extracted for each
observation using this procedure.
| Cluster ID | MOS | PN | % lost |
| RX J0337.7-2522 | 23 421 | 23 611 | 60 |
| RX J0505.3-2849 | 31 851 | 24 983 | 35 |
| RX J0847.2+3449 | 43 793 | - | 50 |
| RX J1120.1+4318 | 18 333 | 16 208 | 18 |
| RX J1325.5-3826 | - | 48 753 | 20 |
| RX J1334.3+5030 | 40 713 | 34 909 | 15 |
| RX J1354.2-0222 | 9090 | 7248 | 73 |
| RX J1701.3+6414 | 9379 | 4382 | 50 |
For clusters RX J1354.2-0222 and RX J1701.3+6414 the high prevalence of proton flares mitigated against the automated filtering procedure, and a manual analysis of the the "curve of growth'' for signal:noise in the cluster target region was employed.
The clusters in our sample are expected to be extended on a scale of
2-3 arc-min, and in order to assess accurately the surface
brightness distribution, a small correction for energy dependent
telescope vignetting must be applied. This was performed by the SAS
task EVIGWEIGHT which assigns a weighting value to each detected
photon, accounting for telescope and CCD efficiency variations (the
latter being negligible by comparison). Thereafter, spectrum
extraction and image product generation is automatically weighted for
the vignetting correction, and response matrices for the on-axis
location can be used![]() .
.
An exposure map was also generated for each camera observation. These maps accounted for spatial variations, such as dead pixels, noisy readout columns and chip gaps, not included in the vignetting correction. The XMM-Newton satellite is usually very stable during observations, so the inter-CCD gaps remain approximately fixed in sky projection. It is therefore important to correct for flux lost from extended cluster regions using the exposure maps. This is especially true for the PN images, because the PN CCDs are smaller and the gaps closer to the target than those in the MOS cameras.
Background subtraction is a very important step in our analysis. Even after the proton flare removal described above (Sect. 3.1), and after masking out point sources, our cluster observations will be contaminated, to varying degrees, by three different background signals; (i) the cosmic X-ray background, (ii) a particle background induced by incident cosmic rays and (iii) some residual soft proton contamination. We will refer to these as the cosmic, particle and proton backgrounds respectively, hereafter. There are two approaches to background subtraction, either one can use the source observation itself (this is known as in-field subtraction), or one can use background template files. The templates are generated by combining several deep, blank field, observations and are especially useful when the source of interest covers a large fraction of the field of view (e.g. a nearby cluster). We have used a combination of both techniques in the analysis below.
For each of the eight clusters in our study, we applied the same rate filtering, vignetting correction and detector-to-sky conversion used for the reduction of the cluster observation, to the background template files provided by the XMM-SOC (Lumb et al. 2002). This allowed us to extract identical physical detector regions for both the cluster and the background using the SAS task ATTCALC. We then re-normalized the background template to account for any differences in the particle background count rates between the cluster and background template observations. This step was necessary because the particle background varies with observation epoch (Sect. 3.3.1). To make this correction, we took advantage of the fact that high energy particles are not focused by the telescope optics, so the particle background count rate can be measured from areas outside the telescope FOV.
We used re-normalized background templates (energy range 0.3-4.5 keV) during the spatial analysis (Sect. 3.5). We also used background templates (energy range 0.3-10 keV) during the spectral analysis of two of our two brightest clusters (RX J1120.1 and RX J1334.3). For this, we employed the so-called "double subtraction'' technique (Arnaud et al. 2001), which involves making an additional correction to compensate for the fact that the Galactic Halo and the Local Hot Bubble component of the diffuse cosmic X-ray background varies significantly across the sky. To determine this correction, we compared off-axis, source free, regions in both the cluster fields and their corresponding background templates. We found the correction to be small, due to the lack of soft X-ray emission features at the high Galactic latitude locations of RX J1120.1 and RX J1334.3. We have used the results from the double subtraction analysis of RX J1120.1 and RX J1334.3 to validate the results from the in-field background subtraction, see below.
For a variety of reasons, e.g. the choice of filter![]() , low signal to
noise, non-zero off-axis angle etc., we were not able to apply the
double subtraction technique to all our clusters. Instead we have to
rely on the in-field technique. The radial dependence of the
vignetting means that this technique is most successful for point
sources, however it should still work well for our clusters since, at
z>0.4, they are barely more extended than the instrument point
spread function (PSF). We illustrate this by considering a cluster
described by a
, low signal to
noise, non-zero off-axis angle etc., we were not able to apply the
double subtraction technique to all our clusters. Instead we have to
rely on the in-field technique. The radial dependence of the
vignetting means that this technique is most successful for point
sources, however it should still work well for our clusters since, at
z>0.4, they are barely more extended than the instrument point
spread function (PSF). We illustrate this by considering a cluster
described by a ![]() -model with
-model with
![]() and a core
radius of 25'' (
and a core
radius of 25'' (
![]() kpc typical values for the clusters in our sample,
Table 5). At a radius enclosing 75% of the counts from such
a cluster, the vignetting is different by less than 1% from the
aim-point value. Therefore we posit that an accurate representation of
the cosmic X-ray background spectrum at the cluster position can be
derived using a
nearby in-field background aperture. For the spectral analysis of our
clusters we generally used an annular background aperture centered on
the source. The annuli were chosen on a case by case basis, but were
typically 2-3' wide with an inner radius no less than 3' from the
cluster center (to ensure that no flux from outlying regions of the
cluster was erroneously removed). We note that in the case of
RX J1325.5, we could not use an annulus, due to the proximity of a very
bright point source (Sect. 4.6). In
Sects. 4.1 and 4.2, we compare the results of
the spectral fitting for the clusters where both in field and double
subtraction could be applied. As we did not find significant
differences, we conclude that the in field background subtraction
technique should be valid for our sample.
kpc typical values for the clusters in our sample,
Table 5). At a radius enclosing 75% of the counts from such
a cluster, the vignetting is different by less than 1% from the
aim-point value. Therefore we posit that an accurate representation of
the cosmic X-ray background spectrum at the cluster position can be
derived using a
nearby in-field background aperture. For the spectral analysis of our
clusters we generally used an annular background aperture centered on
the source. The annuli were chosen on a case by case basis, but were
typically 2-3' wide with an inner radius no less than 3' from the
cluster center (to ensure that no flux from outlying regions of the
cluster was erroneously removed). We note that in the case of
RX J1325.5, we could not use an annulus, due to the proximity of a very
bright point source (Sect. 4.6). In
Sects. 4.1 and 4.2, we compare the results of
the spectral fitting for the clusters where both in field and double
subtraction could be applied. As we did not find significant
differences, we conclude that the in field background subtraction
technique should be valid for our sample.
The ratio of the proton to particle backgrounds is not constant; even
after proton flare mitigation (Sect. 3.1), the proton
background may have a significantly different counting rate in the
cluster observation compared to background template files
(Markevitch 2002). This is illustrated in Fig. 4. The
triangles indicate the ratio of the particle background in the cluster
observation to that in the background template file (Col. 2 in
Table 3). The squares show the equivalent
information for the proton background (Col. 3 in
Table 3). For this comparison, the particle
background was estimated from the ![]() 10 keV count rate in CCD areas
outside the telescope FOV, whereas the proton background was
estimated by subtracting that value from the
10 keV count rate in CCD areas
outside the telescope FOV, whereas the proton background was
estimated by subtracting that value from the ![]() 10 keV count rate
within the FOV. From the Fig. 4, it is clear that the proton
background varies with epoch and is anti-correlated with the particle
background. This anti-correlation can be explained if
10 keV count rate
within the FOV. From the Fig. 4, it is clear that the proton
background varies with epoch and is anti-correlated with the particle
background. This anti-correlation can be explained if
| Cluster ID | Outside FOV | Inside FOV |
| RX J0337.7-2522 | 0.72 | 1.82 |
| RX J0505.3-2849 | 0.70 | 1.27 |
| RX J0847.2+3449 | 0.68 | 2.14 |
| RX J1120.1+4318 | 0.99 | 1.05 |
| RX J1325.5-3826 | 1.05 | |
| RX J1334.3+5030 | 1.00 | 1.23 |
| RX J1354.2-0222 | 0.52 | 3.44 |
| RX J1701.3+6414 | 0.48 | 5.13 |
To examine the likely impact of systematic errors in the proton vignetting correction,
we used the EVIGWEIGHT vignetting corrected background template
files to create an image that was essentially free from proton
contamination. We did so by applying very strict count-rate
filtering. We then made a comparison image by applying less
conservative count-rate filtering to the background template
files. For this we used the filtering criteria derived from the
RX J1701.3 observation (which suffered from unusually high proton
contamination); the comparison is presented in
Fig. 5.
The two count rate images we derived, should be
identical within the noise, except with regard to the proton
background. By dividing one by the other, and then fitting a radial
surface brightness profile, we should therefore be able to get an
impression of how the proton background is vignetted. The results of
this test (in the 0.5-7.0 keV band to emphasize an effect of hard
proton spectrum) are shown in
Fig. 5. We also generated the equivalent figure
using the RX J1354.2 filtering criteria with almost identical results.
From this investigation, we conclude that the proton background is
over-weighted by only a few percent by EVIGWEIGHT even at the
edges of the field of view in observations with significant proton contamination. We
therefore chose to ignore the over-weighting of the proton background
in our analysis, except in the cases of RX J1701.3 and RX J1354.2. For
these, we applied a small (![]() 2%) scaling to the background
spectrum derived from an in-field annulus around the cluster
2%) scaling to the background
spectrum derived from an in-field annulus around the cluster![]() .
.
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{0687fig5.ps} }
\end{figure}](/articles/aa/full/2004/24/aa0687/Timg46.gif) |
Figure 5: Ratio of the surface brightness distributions in blank fields, showing proton contamination in RX J1701.3+6414 field. |
Cluster spectra were extracted from circular regions centred on the cluster centroids, with radii ranging from 90 to 145 arcsec (typically 120'', see Table 5, row 13). From these regions we extracted data from the event list using the recommended pixel selections. For the PN camera we used single and double pixel events (event patterns 0-4) with all the recommended selection flags applied. For the MOS cameras, we used the 0-12 event patterns. We account for background contamination in the spectra using either the double and/or in-field subtraction methods (Sect. 3.3).
Spectral fitting was implemented with the XSPEC v11 package
(Arnaud 1996), using the MEKAL models (Mewe et al. 1986) for a thermal
spectrum, modified with interstellar absorption (McCammon & Sanders 1990)
appropriate for the Galactic column density (Dickey & Lockman 1990). To
facilitate fitting via Chi-square minimization, the spectral files
were re-binned to ensure at least 25 counts per bin in order to
approximate Gaussian statistics. The energy range was 0.3-10 keV.
In general, the following on-axis
response files were used during the fits, epn_ff20_sdY9_filter.rmf for the PN camera and m1(2)_filterv9q20t5r6_all_15.rsp for the MOS1(2)
cameras. Exceptions to this, e.g. during the analysis of RX J1325.5,
are noted below. Fitted spectral parameters are quoted with 1![]() confidence limits on one interesting parameter. The spectral fits were
typically performed simultaneously on the PN, MOS1(2) spectra. Again exceptions to this, e.g. during the analysis of RX J0847.2,
are noted in the relevant sections.
confidence limits on one interesting parameter. The spectral fits were
typically performed simultaneously on the PN, MOS1(2) spectra. Again exceptions to this, e.g. during the analysis of RX J0847.2,
are noted in the relevant sections.
Following Markevitch (1998), we have also investigated the impact of cooling cores on our fitted temperatures, and hence the measured Lx-Tx relation, by performing spectral fits after excising the central region. For all clusters except RX J1701 and RX J1325, a 50 h-150 kpc region was excised. For RX J1701 & 1325 a 120 kpc region was excised (see Sect. 4.7). The results from these fits are given at the beginning of Table 5. See Sect. 5.2.1 for a discussion.
For the luminosity calculations, we adopted a physically meaningful
circular aperture, with a virial radius, ![]() .
We derived
.
We derived ![]() according the
according the
![]() relation of Evrard et al. (1996) for each cluster using
the best fit temperatures from the spectral fits. We note that
uncertainties both in the measured temperature and in the
relation of Evrard et al. (1996) for each cluster using
the best fit temperatures from the spectral fits. We note that
uncertainties both in the measured temperature and in the
![]() relation will introduce a systematic error in the derived Lxvalues. However, this should be insignificant, as very little cluster
flux falls at radii close to the virial radius.
relation will introduce a systematic error in the derived Lxvalues. However, this should be insignificant, as very little cluster
flux falls at radii close to the virial radius.
We integrated the
background-subtracted counts inside ![]() and then corrected for any
cluster flux lost in areas under masked point sources or inter-chip
gaps. The correction factors are given in row 12 of
Table 5. These were derived in a model independent fashion;
the count-rate was accumulated in 1 pixel wide annuli centered on the
cluster. If any pixels within a specific annulus fell in chip gaps or
in the point source masked, the annulus count-rate was scaled up
accordingly. Next, we used XSPEC, together with the appropriate EPIC
response functions, to determine the absorbed 0.3-4.5 keV flux within
and then corrected for any
cluster flux lost in areas under masked point sources or inter-chip
gaps. The correction factors are given in row 12 of
Table 5. These were derived in a model independent fashion;
the count-rate was accumulated in 1 pixel wide annuli centered on the
cluster. If any pixels within a specific annulus fell in chip gaps or
in the point source masked, the annulus count-rate was scaled up
accordingly. Next, we used XSPEC, together with the appropriate EPIC
response functions, to determine the absorbed 0.3-4.5 keV flux within
![]() ,
using the best fit absorbed MEKAL model from our spectral
analysis so that it yielded the measured
,
using the best fit absorbed MEKAL model from our spectral
analysis so that it yielded the measured
![]() count rate (the MEKAL
normalization factors are given in row 10 of Table 5).
For comparison with equivalent ROSAT data such as SHARC or 160SD these
fluxes (converted to the normal ROSAT 0.5-2 keV band) are listed in
row 6 of Table 5. We
then set the hydrogen column density to zero and re-determined the
flux inside a pseudo bolometric band of 0.0-20 keV. From the
unabsorbed bolometric flux, it is trivial to determine the bolometric
luminosity for any given cosmological model. To aid comparisons with
previous work, we give in, row 3 of Table 5, the Lxvalues appropriate for a
count rate (the MEKAL
normalization factors are given in row 10 of Table 5).
For comparison with equivalent ROSAT data such as SHARC or 160SD these
fluxes (converted to the normal ROSAT 0.5-2 keV band) are listed in
row 6 of Table 5. We
then set the hydrogen column density to zero and re-determined the
flux inside a pseudo bolometric band of 0.0-20 keV. From the
unabsorbed bolometric flux, it is trivial to determine the bolometric
luminosity for any given cosmological model. To aid comparisons with
previous work, we give in, row 3 of Table 5, the Lxvalues appropriate for a
![]() ,
,
![]() ,
q0=0.5 model with H0=50 km s-1 Mpc-1 that has been
most frequently used in the past as the parameter set for X-ray cluster studies.
,
q0=0.5 model with H0=50 km s-1 Mpc-1 that has been
most frequently used in the past as the parameter set for X-ray cluster studies.
Also following Markevitch (1998), we estimated the cooling flow
corrected bolometric luminosities by summing counts in a (
![]() )
ring. For clusters other than RX J1701 and RX J1325,
)
ring. For clusters other than RX J1701 and RX J1325, ![]() =
50
h-150 kpc, while for RX J1701 & 1325
=
50
h-150 kpc, while for RX J1701 & 1325
![]() h-150 kpc (see Sect. 4.7). To account for the non-cooling flow flux
falling at
h-150 kpc (see Sect. 4.7). To account for the non-cooling flow flux
falling at
![]() ,
we applied a cluster specific
renormalisation parameter calculated using the best fit
,
we applied a cluster specific
renormalisation parameter calculated using the best fit
![]() -model. We note that our correction approach differs from that
of Markevitch (1998), therein a single multiplicative factor of 1.06
was used.
-model. We note that our correction approach differs from that
of Markevitch (1998), therein a single multiplicative factor of 1.06
was used.
We now discuss our analysis for each cluster in turn. We have ordered our discussion according to the Julian date on which they were observed (Table 1).
Figure 6a shows the vignetting corrected, background
subtracted and co-added (PN+MOS1+MOS2) 0.3-4.5 keV image of
RX J1120.1+4318. Point sources removed during analysis are circled and
their positions listed in Table A.1.
Figure 19 shows the corresponding radial surface
brightness distribution and best fit ![]() model;
model;
![]() ,
,
![]() arcsec
(
arcsec
(
![]() kpc, Table 5).
kpc, Table 5).
From a spectral extraction region with a radius of 145'' and using
the in-field background subtraction technique, we measured the
following temperature, metal abundance and redshift by fitting to the
PN, MOS1 and MOS2 data simultaneously;
Tx= 5.45 +0.26-0.35 keV,
![]() ,
,
![]() .
We note the consistency between the redshift
measured from the X-ray spectrum with the optically determined value
(z=0.60; Romer et al. 2000). The overall
.
We note the consistency between the redshift
measured from the X-ray spectrum with the optically determined value
(z=0.60; Romer et al. 2000). The overall
![]() of the
spectral fit was 390/360 degrees of freedom. During the fit, the
hydrogen column density was fixed at the Galactic value
(
of the
spectral fit was 390/360 degrees of freedom. During the fit, the
hydrogen column density was fixed at the Galactic value
(![]()
![]() atoms cm-2), but we note that, when
left as a free parameter, its best fit value was very similar
(
atoms cm-2), but we note that, when
left as a free parameter, its best fit value was very similar
(![]()
![]() atoms cm-2).
atoms cm-2).
![\begin{figure}
\par {\includegraphics[angle=270,width=8.8cm,clip]{0687fig8.ps} }\end{figure}](/articles/aa/full/2004/24/aa0687/Timg68.gif) |
Figure 8: Spectral fit and residuals for RX J1120.1; black - PN, dark and light grey - MOS1 & 2 (double background subtraction). |
We have also investigated how the spectral fits differ when we treat
the PN and MOS data separately. We find them to be in good
agreement;
![]() keV and
keV and
![]() keV. This is encouraging since, in two other cases (RX J1325.5
and RX J0847.2), we do not have access to data from all three cameras.
We have also been able to subdivide the spectral extraction region
into three radial bins, and determined a crude temperature profile
(Fig. 9). The profile is essentially flat,
indicating that there is not a "cooling flow'' region at the cluster
core (this conclusion is supported by the absence of a central spike
in the surface brightness profile). We note that for the PN/MOS
comparison and for the radial profile, we used the double subtraction
technique to account for the background.
keV. This is encouraging since, in two other cases (RX J1325.5
and RX J0847.2), we do not have access to data from all three cameras.
We have also been able to subdivide the spectral extraction region
into three radial bins, and determined a crude temperature profile
(Fig. 9). The profile is essentially flat,
indicating that there is not a "cooling flow'' region at the cluster
core (this conclusion is supported by the absence of a central spike
in the surface brightness profile). We note that for the PN/MOS
comparison and for the radial profile, we used the double subtraction
technique to account for the background.
The RX J1120.1 observation described here have been previously analyzed
and interpreted in an earlier paper in this series
(Arnaud et al. 2002). The analysis procedures developed in that paper have
formed the basis of the analysis of the eight clusters described
here. For example, the vignetting correction technique used in
Arnaud et al. (2002) has been subsequently implemented in SAS as the EVIGWEIGHT routine mentioned above. However, there are certain
differences in our respective data analysis techniques, even with
regard to the RX J1120.1 observation. For example, we use updated
calibration information and an updated SAS processing version. We also
used a different method (3-sigma clipping) for the GTI filtering. We
have also adopted the in-field background subtraction method as the
standard for our cluster analysis (in Arnaud et al. 2002, only the double
subtraction technique was used). Finally, we note our use of the both
single and double PN events, compared to the selection of single
events by Arnaud et al. (2002). In general the revised analysis of
RX J1120.1 has yielded very similar results to Arnaud et al. (2002) and we
concur that, given its isothermal temperature profile and the absence
of significant substructure, RX J1120.1 is consistent with being a
relaxed cluster. It is noteworthy, however, that in Arnaud et al. (2002) the
mean temperature values determined using only MOS data differed from
those determined using only PN data by more than 1 keV;
![]() keV and
keV and
![]() keV. By contrast, we measured temperatures that differed by only 8%
(see above). This improvement is most likely attributable to the
improved calibration that has become available since Arnaud et al. (2002) was
published. For completeness we compare in Table 4 the
values derived for various fitted parameters in the two analyses. For
consistency with Arnaud et al. (2002), we quote the mean temperature derived
using the double subtraction technique (in Table 5 we quote
the value from based on the in field subtraction technique).
keV. By contrast, we measured temperatures that differed by only 8%
(see above). This improvement is most likely attributable to the
improved calibration that has become available since Arnaud et al. (2002) was
published. For completeness we compare in Table 4 the
values derived for various fitted parameters in the two analyses. For
consistency with Arnaud et al. (2002), we quote the mean temperature derived
using the double subtraction technique (in Table 5 we quote
the value from based on the in field subtraction technique).
|
|
EdS Lx |
|
|
| (1044 erg s-1) | |||
|
|
|
|
|
|
|
|
|
|
Figure 6b shows the image of the
RX J1334.3+5030 field. Point sources removed during analysis are circled and
their positions listed in Table A.1.
Figure 19 shows the corresponding
radial surface brightness distribution and best fit ![]() model;
model;
![]() ,
,
![]() arcsec
(
arcsec
(
![]() kpc, Table 5).
kpc, Table 5).
From a spectral extraction region with a radius of 120'' and using
the in-field background subtraction technique, we measured the
following temperature and metal abundance;
Tx=5.20+0.26-0.28 keV,
![]() (Fig. 10). The overall
(Fig. 10). The overall
![]() of the spectral fit was 464/473 degrees of freedom.
The hydrogen column was fixed at the Galactic
value (
of the spectral fit was 464/473 degrees of freedom.
The hydrogen column was fixed at the Galactic
value (![]()
![]() atoms cm-2), but we note that,
when left as a free parameter, its best fit value was very similar
(
atoms cm-2), but we note that,
when left as a free parameter, its best fit value was very similar
(![]()
![]() atoms cm-2). Likewise, the
redshift was fixed at its optically derived value of z=0.62 (Romer
et al. 2000), but when left as a free parameter, its best fit value
was
atoms cm-2). Likewise, the
redshift was fixed at its optically derived value of z=0.62 (Romer
et al. 2000), but when left as a free parameter, its best fit value
was
![]() .
The derived values for the bolometric luminosity
and absorbed flux inside the viral radius are given in
Table 5. We were also able to apply the double subtraction
technique to these data and derived a consistent mean temperature
value;
.
The derived values for the bolometric luminosity
and absorbed flux inside the viral radius are given in
Table 5. We were also able to apply the double subtraction
technique to these data and derived a consistent mean temperature
value;
![]() keV.
keV.
![\begin{figure}
\par {\includegraphics[angle=270,width=8.8cm,clip]{0687fig10.ps} }\end{figure}](/articles/aa/full/2004/24/aa0687/Timg95.gif) |
Figure 10: Spectral fit and residuals for RX J1334.3; black - PN, dark & light gray - MOS1 & 2 (in-field background subtraction). |
From a spectral extraction region with a radius of 120'' and using
the in-field background subtraction technique, we measured the
following temperature, metal abundance and redshift;
![]() keV,
keV,
![]() ,
,
![]() (Fig. 11). The
overall
(Fig. 11). The
overall
![]() of the spectral fit was 193/214 degrees of
freedom. We note the consistency between the redshift measured from
the X-ray spectrum with the optically determined value (z=0.577;
Burke et al. 2003). The hydrogen column density was
fixed at the Galactic value (
of the spectral fit was 193/214 degrees of
freedom. We note the consistency between the redshift measured from
the X-ray spectrum with the optically determined value (z=0.577;
Burke et al. 2003). The hydrogen column density was
fixed at the Galactic value (![]()
![]() atoms
cm-2), when left as a free parameter, its best
fit value was very similar (
atoms
cm-2), when left as a free parameter, its best
fit value was very similar (![]()
![]() atoms cm-2). The derived values for the bolometric luminosity
and absorbed flux inside the viral radius are given in
Table 5.
atoms cm-2). The derived values for the bolometric luminosity
and absorbed flux inside the viral radius are given in
Table 5.
The RX J0505.3-2849 field is shown in Fig. 6d.
Four point sources removed during analysis are circled
and their positions listed in Table A.1. Tentative
identifications of these sources with objects in the UK APM survey
(Maddox et al. 1990) suggest an absolute astrometric accuracy for our
observations of ![]() 2 arcsec.
Figure 19 shows the corresponding radial surface
brightness distribution and best fit
2 arcsec.
Figure 19 shows the corresponding radial surface
brightness distribution and best fit ![]() model;
model;
![]() and
and
![]() arcsec
(
arcsec
(
![]() kpc, Table 5).
kpc, Table 5).
From a spectral extraction region with a radius of 120'' and using
the in-field background subtraction technique, we measured;
![]() keV,
keV,
![]() (Fig. 12). The overall
(Fig. 12). The overall
![]() of the
spectral fit was 279/248 degrees of freedom. The fixed Galactic hydrogen
value was
of the
spectral fit was 279/248 degrees of freedom. The fixed Galactic hydrogen
value was ![]()
![]() atoms cm-2), compared with a
free
fit parameter, of
atoms cm-2), compared with a
free
fit parameter, of ![]()
![]() atoms cm-2). The
redshift was fixed at its optically derived value of z=0.51 (Burke et al. 2003), but when
left as a free parameter, its best fit value was
atoms cm-2). The
redshift was fixed at its optically derived value of z=0.51 (Burke et al. 2003), but when
left as a free parameter, its best fit value was
![]() .
As a test, we have
also performed a spectral fit without excluding the four point
sources. We find that, within the errors, the fitted temperature was
unchanged.
.
As a test, we have
also performed a spectral fit without excluding the four point
sources. We find that, within the errors, the fitted temperature was
unchanged.
Figure 20 shows the radial surface brightness
distribution for RX J0847.2 and the best fit ![]() model;
model;
![]() and
and
![]() arcsec.
(
arcsec.
(
![]() kpc, Table 5).
From a spectral extraction region with a radius of 120'' and using
the in-field background subtraction technique, we measured
Tx=3.62+0.58-0.51 keV,
kpc, Table 5).
From a spectral extraction region with a radius of 120'' and using
the in-field background subtraction technique, we measured
Tx=3.62+0.58-0.51 keV,
![]() (Fig. 13). The overall
(Fig. 13). The overall
![]() of the spectral fit was 152/180 degrees of freedom.
The fixed hydrogen column density was
of the spectral fit was 152/180 degrees of freedom.
The fixed hydrogen column density was ![]()
![]() atoms cm-2,
as a free parameter, its best fit value was
atoms cm-2,
as a free parameter, its best fit value was ![]()
![]() atoms cm-2. The redshift was fixed at its optically derived value of z=0.56but its best fit value
was
atoms cm-2. The redshift was fixed at its optically derived value of z=0.56but its best fit value
was
![]() .
As a test, we have also performed a spectral fit
without excluding the four point sources. Doing so changed the fitted
temperature by 0.1 keV and the measured flux by
.
As a test, we have also performed a spectral fit
without excluding the four point sources. Doing so changed the fitted
temperature by 0.1 keV and the measured flux by ![]() 10%.
10%.
We have also estimated the temperature of the second cluster in the
field, XMMU J084701.8+345117. For this we used a spectral extraction
radius of 80 arcsec and the in field background subtraction technique. We do
not have an independent estimate of the cluster redshift, and it
cannot be constrained by the X-ray spectrum, so we have assumed that
the cluster lies at the same redshift as RX J0847.2 (z=0.56). We have
also fixed the metal abundance to be Z=0.3 and the hydrogen
column density to the same Galactic value. We measure a cluster
temperature of
Tx=1.8+1.0-0.4 keV and a corresponding
(
![]() ,
0.5-2 keV) flux and bolometric luminosity of
,
0.5-2 keV) flux and bolometric luminosity of ![]() 10- 14 erg cm-2 s-1 and
10- 14 erg cm-2 s-1 and
![]() erg s-1 respectively. These results are
consistent with measured low red-shift
Lx-Tx relations.
erg s-1 respectively. These results are
consistent with measured low red-shift
Lx-Tx relations.
The data for this cluster were obtained by kind permission of Guaranteed Time holder M Watson, from an observation of the nearby object IRAS 13224-3809. Unfortunately for our own purposes, this bright source had been observed in the MOS cameras in a "Window'' mode of readout on the central CCDs in order to minimize effects of photon pile-up, and consequently the area of focal plane containing the SHARC cluster was not exposed. Therefore, our spatial and spectral analysis is restricted to the PN camera data only. Figure 7b shows the vignetting corrected, background subtracted 0.3-4.5 keV PN image of the region surrounding IRAS 13224-3809. Clusters RX J1325.5-3826 and RX J1325.0-3814 (see below) are labeled, as is the streak corresponding to the "out of time'' events from IRAS 13224-3809. IRAS 13224-3809 is bright enough that the "spider'' like structure in the PSF is visible around it. Given the proximity of the cluster to the IRAS source, the surface brightness profile for RX J1325.5-3826 (Fig. 20) was extracted from manually selected clean regions that avoided the IRAS 13224-3809 PSF.
For the ![]() model fitting, a PSF appropriate for
the PN at the off-axis angle of the cluster was used (for all the
other clusters in our sample, we had used the on-axis PSF). The best fit
parameters in the spatial fit are
model fitting, a PSF appropriate for
the PN at the off-axis angle of the cluster was used (for all the
other clusters in our sample, we had used the on-axis PSF). The best fit
parameters in the spatial fit are
![]() and
and
![]() arcsec (
arcsec (
![]() kpc,
Table 5). There is evidence for possible excess brightness
in the inner bins of the radial profile. This may be in an indication
of a central cooling core, but we do not have adequate signal to noise
to confirm this spectroscopically. Following the procedure adopted for
RX J1701.3 (see below) we also performed a
kpc,
Table 5). There is evidence for possible excess brightness
in the inner bins of the radial profile. This may be in an indication
of a central cooling core, but we do not have adequate signal to noise
to confirm this spectroscopically. Following the procedure adopted for
RX J1701.3 (see below) we also performed a ![]() fit after exclusion
of the core 120 kpc and found a value for
fit after exclusion
of the core 120 kpc and found a value for ![]() of
of
![]() ,
given a fixed
,
given a fixed ![]() of 200
h50-1 kpc (we fixed this value
arbitrarily to match typical cluster values).
of 200
h50-1 kpc (we fixed this value
arbitrarily to match typical cluster values).
We used a 90'' radius extraction region to fit the spectrum from
this cluster. This is a smaller region than was used for the other
clusters (120'' or 145'', Table 5) because of the
proximity of IRAS 13224-3809. Even though the proton background was
low enough in this exposure to permit spectral measurements using the
double subtraction technique, we decided to use instead only the
in-field background subtraction technique. This was because we wanted
to mimic the off-axis angle dependence of the point source
contamination. Rather than using an annulus around the cluster to
determine the background, we used two source and streak free circular
regions at the same off-axis angle as the cluster. From the
background subtracted PN spectrum, we measured the following
temperature, metal abundance and redshift;
Tx=4.15+0.4-0.3 keV,
Z=0.31 +0.19-0.17,
![]() (Fig. 14). We note the consistency between the
redshift measured from the X-ray spectrum with the optically
determined value (z=0.445; Burke et al. 2003). The overall
(Fig. 14). We note the consistency between the
redshift measured from the X-ray spectrum with the optically
determined value (z=0.445; Burke et al. 2003). The overall
![]() of the spectral fit was 229/242 degrees of
freedom. The fixed and free hydrogen column density values were
of the spectral fit was 229/242 degrees of
freedom. The fixed and free hydrogen column density values were
![]()
![]() atoms cm-2 and 4.5
atoms cm-2 and 4.5
![]() atoms cm-2 respectively.
atoms cm-2 respectively.
The cluster is observed close to the edge of the outer CCDs,
preventing the use of an extraction region large enough to correspond
with the virial radius. Within a
radius ![]() 500
h50-1 kpc, the measured flux and bolometric luminosity are 6.1
(
500
h50-1 kpc, the measured flux and bolometric luminosity are 6.1
(![]() 0.3) 10-14 erg cm-2 s-1 (0.5-2 keV) and
0.3) 10-14 erg cm-2 s-1 (0.5-2 keV) and
![]() erg s-1 respectively. This combination of Tx and
Lx are not consistent with the measured
Lx-Tx relation for nearby clusters. For example, for Tx=3.2 keV, one would expect a bolometric luminosity of
erg s-1 respectively. This combination of Tx and
Lx are not consistent with the measured
Lx-Tx relation for nearby clusters. For example, for Tx=3.2 keV, one would expect a bolometric luminosity of
![]() erg s-1 based on the Markevitch (1998) relation, and is probably
due mainly to the missing flux outside our spectral extraction radius.
erg s-1 based on the Markevitch (1998) relation, and is probably
due mainly to the missing flux outside our spectral extraction radius.
This cluster was observed during an exposure scheduled near the end of an orbit, where the spacecraft was approaching the particle belts. Not only were the spacecraft operations terminated prematurely, but most of the exposure was dominated by high soft proton background from the edge of the particle belts. Fortunately this is one of the brightest clusters in our sample and we were still able to produce acceptable quality images and spectra.
Figure 7c shows the image of the RX J1701.3+6414 field. Two nearby sources are marked in the figure; a QSO (HS1700+6416) and a known cluster (A2246).
The XMM-Newton data indicate an anomalously low ![]() value
in the
value
in the ![]() -fit, and this is supported by CHANDRA data
(Vikhlinin et al. 2002) where this cluster was observed with a
suspected cooling flow central brightness enhancement. We therefore excluded the central bins (120
h50-1 kpc)
and fixed the
-fit, and this is supported by CHANDRA data
(Vikhlinin et al. 2002) where this cluster was observed with a
suspected cooling flow central brightness enhancement. We therefore excluded the central bins (120
h50-1 kpc)
and fixed the ![]() to the CHANDRA value of 0.5 arcmin (204 kpc). Figure 20 shows the
corresponding radial surface brightness distribution and resulting best fit
to the CHANDRA value of 0.5 arcmin (204 kpc). Figure 20 shows the
corresponding radial surface brightness distribution and resulting best fit
![]() model;
model;
![]() ,
,
![]() arcsec. This
value for
arcsec. This
value for ![]() is consistent with the CHANDRA measurement
(
is consistent with the CHANDRA measurement
(
![]() ).
).
From a spectral extraction region with a radius of 120'', we measured the
following temperature, metal abundance and redshift (without core excision);
Tx=4.5+1.5-1.0 keV,
![]() ,
,
![]() (Fig. 15).
The overall
(Fig. 15).
The overall
![]() of the spectral fit was 58/53 degrees of freedom. The hydrogen column density was
fixed at the Galactic value (
of the spectral fit was 58/53 degrees of freedom. The hydrogen column density was
fixed at the Galactic value (![]()
![]() atoms cm-2), and as a free parameter, its best
fit value was very similar (
atoms cm-2), and as a free parameter, its best
fit value was very similar (![]()
![]() atoms cm-2).
atoms cm-2).
After excluding the 120 kpc cooling flow region we obtain
![]() keV. The derived values for the bolometric luminosity and
absorbed flux inside the viral radius are given in
Table 5. We were unable to apply the double subtraction
technique to these data because of the enhanced proton background
during the observation (see Fig. 5). The poorer
quality of data in this observation limits the quality of determination of T and L. Agreement with the CHANDRA data is acceptable for the
temperature, but not the luminosity (
keV. The derived values for the bolometric luminosity and
absorbed flux inside the viral radius are given in
Table 5. We were unable to apply the double subtraction
technique to these data because of the enhanced proton background
during the observation (see Fig. 5). The poorer
quality of data in this observation limits the quality of determination of T and L. Agreement with the CHANDRA data is acceptable for the
temperature, but not the luminosity (![]() keV and
keV and
![]() erg/s respectively).
erg/s respectively).
The RX J1354.2-0222 field is shown in Fig. 7d.
A point source that was removed during analysis is
circled and its position listed in
Table A.1. Figure 20 shows the
corresponding radial surface brightness distribution and best fit
![]() model that gives
model that gives
![]() and
and
![]() arcsec (
arcsec (
![]() kpc, Table 5).
kpc, Table 5).
From a spectral extraction region with a radius of 120'', and using
the in-field background subtraction technique, we measured;
Tx=3.66+0.6-0.5 keV,
![]() ,
(Fig. 16). The overall
,
(Fig. 16). The overall
![]() of
the spectral fit was 120/147 degrees of freedom. The fixed Galactic
hydrogen column value was
of
the spectral fit was 120/147 degrees of freedom. The fixed Galactic
hydrogen column value was ![]()
![]() atoms cm-2,
but
atoms cm-2,
but
![]()
![]() atoms cm-2) when free. The
redshift best fit value was
atoms cm-2) when free. The
redshift best fit value was
![]() .
Similarly to RX J1701.3, we were unable to apply the double-background
subtraction technique to these data because of the enhanced proton
background (see Fig. 5).
.
Similarly to RX J1701.3, we were unable to apply the double-background
subtraction technique to these data because of the enhanced proton
background (see Fig. 5).
Table 5 summarizes our analysis of the eight cluster
observations described above. The mean elemental abundance (
![]() ), core radius (
), core radius (
![]() kpc) and
kpc) and ![]() (
(
![]() ), are consistent with typical values measured at low
redshift (e.g. Fukazawa et al. 1998; Jones & Forman 1999; Mohr et al. 1999).
The clusters were
derived from well understood surveys (SHARC and 160SD) and thus should
be representative of the cluster population as a whole at these
redshifts. We have used our observations to determine the
Lx-Tx relation at
0.45<z<0.62 and to investigate
evolutionary effects. We plot luminosity versus temperature, with one
sigma errors, for the 8 cluster targets in Fig. 17,
using
the values
), are consistent with typical values measured at low
redshift (e.g. Fukazawa et al. 1998; Jones & Forman 1999; Mohr et al. 1999).
The clusters were
derived from well understood surveys (SHARC and 160SD) and thus should
be representative of the cluster population as a whole at these
redshifts. We have used our observations to determine the
Lx-Tx relation at
0.45<z<0.62 and to investigate
evolutionary effects. We plot luminosity versus temperature, with one
sigma errors, for the 8 cluster targets in Fig. 17,
using
the values
![]() ,
,
![]() of Table 5. The
errors are clearly dominated by those of the temperature
measurements.
of Table 5. The
errors are clearly dominated by those of the temperature
measurements.
Characterizing the
Lx-Tx relation as
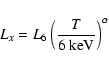 |
(1) |
To characterize the possible evolution with z, we assume
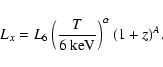 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{0687fig19a.ps}\hspace*{1.2...
...s}\hspace*{1.2cm}
\includegraphics[width=8.1cm,clip]{0687fig19c.ps}
\end{figure}](/articles/aa/full/2004/24/aa0687/Timg185.gif) |
Figure 19:
Surface brightness distribution of clusters, compared with
best |
![\begin{figure}
\par\includegraphics[height=5.6cm,width=8.25cm,clip]{0687fig20a.p...
...5cm}
\includegraphics[height=5.6cm,width=7.9cm,clip]{0687fig20c.ps}
\end{figure}](/articles/aa/full/2004/24/aa0687/Timg188.gif) |
Figure 20:
Surface brightness distribution of clusters, compared with
best |
The value of A has important implications for our understanding
of structure formation and cluster evolution. In a self-similar model
(Kaiser 1981) cluster X-ray properties are driven by gravitational
processes, such as shock heating, and a value of ![]() would be
expected in most cosmological models. A self-similar EdS model predicts
exactly 1.5, and the value is only slightly different in a low density
concordance model, the correction due to the redshift dependence of the
virial density (Bryan & Norman 1998) being small.
In a model where the cluster X-ray properties are influenced by
non-gravitational processes, such as energy injection by AGN's or
supernovae, lower values of A are predicted (e.g. Tozzi & Norman 2001).
The evolution deduced from our observations assuming an EdS model is significantly below the predicted value. Adopting a low density
concordance model, on the other hand, leads to a value consistent with
predictions. We conclude that there is now evidence
from both XMM-Newton and Chandra for an evolutionary trend in the
Lx-Tx relation.
would be
expected in most cosmological models. A self-similar EdS model predicts
exactly 1.5, and the value is only slightly different in a low density
concordance model, the correction due to the redshift dependence of the
virial density (Bryan & Norman 1998) being small.
In a model where the cluster X-ray properties are influenced by
non-gravitational processes, such as energy injection by AGN's or
supernovae, lower values of A are predicted (e.g. Tozzi & Norman 2001).
The evolution deduced from our observations assuming an EdS model is significantly below the predicted value. Adopting a low density
concordance model, on the other hand, leads to a value consistent with
predictions. We conclude that there is now evidence
from both XMM-Newton and Chandra for an evolutionary trend in the
Lx-Tx relation.
Previous studies
of
Lx-Txevolution based on either ASCA (e.g. Mushotzky & Scharf 1997; Allen & Fabian 1998;
Novicki et al. 2002; Sadat et al. 1998), ROSAT PSPC (e.g. Fairley et al. 2000)
or Chandra
(e.g. Borgani et al. 2001; Holden et al. 2002) temperature measurements
found results consistent with no evolution (Sadat et al. 1998). When these studies quote values
for A, these values are generally smaller than those measured by us or
Vikhlinin et al. (2002), but are usually still at least one sigma
away from A =0.
Sadat et al. (1998)
found a positive evolution
![]() for
for
![]() and Novicki et al. (2002)
and Novicki et al. (2002)
![]() for
for
![]() ,
and
,
and
![]() for
for
![]() ,
,
![]() respectively. It is clear that we are beginning to
probe evidence that
Lx-Tx evolution, although
many more clusters need to be
studied, and systematic biases (see below) examined in detail, before
solid conclusions regarding structure formation models can be drawn.
respectively. It is clear that we are beginning to
probe evidence that
Lx-Tx evolution, although
many more clusters need to be
studied, and systematic biases (see below) examined in detail, before
solid conclusions regarding structure formation models can be drawn.
We have made every effort to ensure that the
Lx-Tx relation
presented above is robust. We have adopted a uniform approach to the
spatial and spectral analysis of the eight clusters in the sample. We
have excised regions with clear signs of point source contamination
before extracting spectra and surface brightness profiles. We have not
used ![]() -models to calculate total cluster count rates, but have
rather summed up the counts within a viral radius. We have tried to
ensure that our approach to background subtraction does not bias the
measured cluster parameters (see below). We have used measured
temperatures to make conversions between count rates and fluxes and,
where possible, we have used data from all three EPIC cameras to
derive Lx and Tx values. For RX J0847.2 and
RX J1325.5, data were not available from all three cameras. However, we
are confident that the derived quantities for these two clusters are
robust, as we have shown, using the RX J1120.1 observation, that
PN-only or MOS-only spectra are in excellent agreement.
-models to calculate total cluster count rates, but have
rather summed up the counts within a viral radius. We have tried to
ensure that our approach to background subtraction does not bias the
measured cluster parameters (see below). We have used measured
temperatures to make conversions between count rates and fluxes and,
where possible, we have used data from all three EPIC cameras to
derive Lx and Tx values. For RX J0847.2 and
RX J1325.5, data were not available from all three cameras. However, we
are confident that the derived quantities for these two clusters are
robust, as we have shown, using the RX J1120.1 observation, that
PN-only or MOS-only spectra are in excellent agreement.
The background subtraction has been complicated by the extended nature of the targets and the high proton flare contamination in some of the observations. We used background template files during the spatial analysis. These files covered a limited energy range (0.3-4.5 keV), to minimize any calibration uncertainties. They were filtered using the same rate filtering criteria as their respective cluster observation and were normalized to it using the particle background rates in the CCD regions outside the FOV. For various reasons (see Sect. 3.3), we did not use the background templates for the spectral analysis. Instead, we adopted an in-field background subtraction technique. With this method comes the concern that the proton background can be over-vignetted. We have checked for this by applying a different method, the double subtraction technique, to the RX J1120.1 and RX J1334.3 observations. We found that the results from both techniques agree within the statistical errors. For the two observations with the worst proton flare contamination, RX J1354.2 and RX J1701.3, we applied a 2% scaling to the in-field background spectrum to compensate for potential over-vignetting of the proton background. In Fig. 5 we demonstrate that this over-vignetting should not present a problem for the other clusters in our sample.
Despite all these quality controls, we still cannot rule out the possibility of there being some systematic bias in our results. We discuss possible sources of such bias and the potential impact on our claimed Lx-Tx evolution below.
Cooling cores have the joint effect of boosting
the cluster luminosity and of reducing the measured global cluster
temperature. These effects have been shown to introduce scatter in the
Lx-Tx relation and to modify its slope
(Markevitch 1998; Allen & Fabian 1998). Various approaches have been taken to alleviate
the effects of cooling cores on measured
Lx-Txrelations, e.g. by excluding cooling core clusters from the analysis, Arnaud & Evrard (1999), by fitting two temperature models (Ikebe et al. 2002), by
masking the central regions from obvious cooling core clusters
(Vikhlinin et al. 2002), or by masking the central regions from all clusters
(Markevitch 1998). Based on the images (Figs. 6 and 7) and radial profiles (Figs. 19 and 20 ) of the eight clusters in our sample, we do not
expect cooling cores to have much, if any, impact on the measured Lx and Tx values; only RX J1701.3 and RX J1325.5 show
evidence of a central surface brightness excess. We have investigated
this by comparing the results before and after excising a circular
region![]() from the cluster cores.
from the cluster cores.
The results of the re-analysis can be found in
Table 5, (rows 4 and 5). Temperatures changed very little - always within the
statistical error - after we excised the central
r=50 h50-1kpc region.
In two cases,
(RX J1120.1 and RX J1701.3), the luminosity changes by
more than ![]() ,
but still by only 5% and 9% respectively.
Without the excision the best fit
Lx-Txrelation is
,
but still by only 5% and 9% respectively.
Without the excision the best fit
Lx-Txrelation is
![]() erg s-1 and
erg s-1 and
![]() for an
for an
![]() ,
H0=50 km s-1 Mpc-1 cosmology
at a typical redshift
,
H0=50 km s-1 Mpc-1 cosmology
at a typical redshift
![]() .
In
summary, we find the
Lx-Tx relations before and after
the core excision are consistent within the errors. However, we
caution that some residual cooling flow contamination may still remain
after this excision;
.
In
summary, we find the
Lx-Tx relations before and after
the core excision are consistent within the errors. However, we
caution that some residual cooling flow contamination may still remain
after this excision;
![]() ,
corresponding to an
encircled energy fraction of a little under 50% of the on-axis mirror
PSFs.
,
corresponding to an
encircled energy fraction of a little under 50% of the on-axis mirror
PSFs.
Our
Lx-Tx evolution result implies that high redshift
clusters in our sample are more luminous than clusters of the same
temperature at lower redshift. We interpret this as evidence for a
general evolutionary trend in the
Lx-Txrelation, but
it might also reflect an underlying selection bias in the cluster
catalogs from which the sample was drawn, e.g. if the SHARC and 160SD
surveys were biased toward merging systems. It is possible that the
luminosity and temperature of clusters can change dramatically during
the process of a major merging event (Ricker & Sarazin 2001). Based on the
XMM-Newton images of the 8 clusters studied here
(Figs. 6 and 7), such a bias does
not appear to exist; only RX J1354 has evidence for a possible
double component, and excluding this from the best fit
Lx-Txrelation changes the luminosity normalisation only ![]() 2%. As long
as the angular resolution of observations allows sufficient
discrimination against obvious mergers, then presumably an ensemble
sample of local and distant clusters are similarly affected by merger
boosting of luminosity.
2%. As long
as the angular resolution of observations allows sufficient
discrimination against obvious mergers, then presumably an ensemble
sample of local and distant clusters are similarly affected by merger
boosting of luminosity.
Moreover, we find no evidence for any incompleteness
in the SHARC and 160SD surveys, at least in the small area covered by
these observations. No new clusters were found in the fields
surrounding the seven SHARC clusters in our sample. In the field of
the 160SD cluster, RX J0847.2, we have discovered a new X-ray cluster
(XMMU J084701.8+345117). However this cluster was too faint to have been
included in the original 160SD survey. We estimate the (
![]() )
flux of this
object to be
)
flux of this
object to be
![]() erg cm-2 s-1 (based on a fitted
temperature of Tx=1.8 keV and an assumed redshift of z=0.56),
compared to the 160SD flux limit of
erg cm-2 s-1 (based on a fitted
temperature of Tx=1.8 keV and an assumed redshift of z=0.56),
compared to the 160SD flux limit of
![]() erg cm-2 s-1, so
this cluster is too faint to have been included in the original 160SD survey. In summary we do not find evidence for any intrinsic bias in
the SHARC or 160SD survey selection functions that could mimic
Lx-Tx evolution.
erg cm-2 s-1, so
this cluster is too faint to have been included in the original 160SD survey. In summary we do not find evidence for any intrinsic bias in
the SHARC or 160SD survey selection functions that could mimic
Lx-Tx evolution.
Another possible way to mimic the claimed evolution would be to systematically overestimate the Lx values. We have investigated this by comparing our flux measurements to those published in several works (Romer et al. 2000; Burke et al. 2003; Vikhlinin et al. 1998). We report here that a systematic offset does appear to exist, but in the opposite direction to that needed to mimic evolution. The XMM-Newton fluxes quoted in Table 5 are all lower than previously determined values, typically by 20% but as much as by 40% in the case of RX J0505.3. We note that this discrepancy persists regardless of the ROSAT catalog from which the cluster was selected. The average discrepancy between the Southern SHARC (4 clusters), Bright SHARC (3 clusters) and 160SD (3 clusters) fluxes and the XMM-Newton fluxes is 22%, 21% and 16% respectively.
Improvements in point source rejection, count rate to flux conversions
and the signal to noise have meant that the typical statistical error
on the XMM-Newton determined fluxes in Table 5 is
![]() ,
compared to
,
compared to
![]() for the ROSAT determinations.
Therefore, even accounting for a possible offset in the absolute cross
calibration of the two observatories, it is clear that a systematic
flux offset does exist. There are likely to be several reasons for
this offset. Of these, the use of an incorrect spatial model, to
convert between an aperture flux and a total flux, is probably the
most significant. As shown in Romer et al. (2000), the use of a
generic (
for the ROSAT determinations.
Therefore, even accounting for a possible offset in the absolute cross
calibration of the two observatories, it is clear that a systematic
flux offset does exist. There are likely to be several reasons for
this offset. Of these, the use of an incorrect spatial model, to
convert between an aperture flux and a total flux, is probably the
most significant. As shown in Romer et al. (2000), the use of a
generic (
![]() ,
,
![]() kpc), rather than best
fit,
kpc), rather than best
fit, ![]() -model resulted in a typical enhancement of 10% in the
total cluster flux. In our XMM-Newton analysis, we do not use the
-model resulted in a typical enhancement of 10% in the
total cluster flux. In our XMM-Newton analysis, we do not use the
![]() -model fits to determine the total flux. Instead we directly sum
up the counts within a virial radius. For some clusters this
difference in approach can explain the entire ROSAT to XMM-Newton
discrepancy. For example, in the case of RX J1334.3, our estimate of
-model fits to determine the total flux. Instead we directly sum
up the counts within a virial radius. For some clusters this
difference in approach can explain the entire ROSAT to XMM-Newton
discrepancy. For example, in the case of RX J1334.3, our estimate of
![]() is almost identical to the r80 radius within which 80% of
the total flux from a generic
is almost identical to the r80 radius within which 80% of
the total flux from a generic ![]() -model would
fall. Romer et al. (2000) divided the ROSAT counts within r80 by
0.8 to estimate the total count rate. For RX J1334.3 this division
would artificially boost the flux by 25% which more than accounts for
the 22% the discrepancy between the XMM-Newton and Bright SHARC
values.
-model would
fall. Romer et al. (2000) divided the ROSAT counts within r80 by
0.8 to estimate the total count rate. For RX J1334.3 this division
would artificially boost the flux by 25% which more than accounts for
the 22% the discrepancy between the XMM-Newton and Bright SHARC
values.
For the four Southern SHARC clusters in our sample, we have
recalculated the total ROSAT PSPC fluxes using the ![]() and
and ![]() values given in Table 5 (in Burke et al. 2003 generic values
were used;
values given in Table 5 (in Burke et al. 2003 generic values
were used;
![]() ,
,
![]() kpc). By doing so, we
improve the consistency between the ROSAT and XMM-Newton fluxes to
within 5% for RX J1354.2 and RX J1325.5 and within 15% for
RX J0337.7. For RX J0505.3 there remains a large, 35%, discrepancy
which requires further investigation.
kpc). By doing so, we
improve the consistency between the ROSAT and XMM-Newton fluxes to
within 5% for RX J1354.2 and RX J1325.5 and within 15% for
RX J0337.7. For RX J0505.3 there remains a large, 35%, discrepancy
which requires further investigation.
For the three Bright SHARC clusters in our sample, we have gone back
to the original Romer et al. (2000) data and measured count rates
inside ![]() .
Doing so reduces the ROSAT determined flux by
.
Doing so reduces the ROSAT determined flux by
![]() in the case of both RX J1120.1 and RX J1334.3, i.e. so that they
are
in the case of both RX J1120.1 and RX J1334.3, i.e. so that they
are
![]() lower than the values quoted in Table 5. In
the case of RX J1701.3, the measured ROSAT flux actually increased
slightly when measured inside
lower than the values quoted in Table 5. In
the case of RX J1701.3, the measured ROSAT flux actually increased
slightly when measured inside ![]() rather than r80. On closer
examination of the ROSAT data, it was apparent that the nearby QSO and
cluster (see Fig. 7) were contaminating both the
source and background apertures in the PSPC image. When the source and
background were accumulated only from the (source free) region to the
West of the cluster, the ROSAT flux within
rather than r80. On closer
examination of the ROSAT data, it was apparent that the nearby QSO and
cluster (see Fig. 7) were contaminating both the
source and background apertures in the PSPC image. When the source and
background were accumulated only from the (source free) region to the
West of the cluster, the ROSAT flux within ![]() dropped to within
dropped to within
![]() of the XMM-Newton determined value. These examples
demonstrate the importance of using XMM-Newton to re-calculate fluxes
and luminosities for high redshift clusters detected at low signal to
noise by ROSAT. We stress that, despite these flux uncertainties, the
SHARC and 160SD catalogs are still fair representations of the
underlying cluster population and can still be used to probe the
Lx-Tx relation. It is also important to note that the
these flux uncertainties do not apply to the ROSAT observations used
by Markevitch (1998) to determine Lx values for the 30 low
redshift clusters in his
Lx-Tx analysis. Those
observations have exquisite signal to noise, so that the Lxvalues derived from them will be limited only by the absolute
calibration of the instrument.
of the XMM-Newton determined value. These examples
demonstrate the importance of using XMM-Newton to re-calculate fluxes
and luminosities for high redshift clusters detected at low signal to
noise by ROSAT. We stress that, despite these flux uncertainties, the
SHARC and 160SD catalogs are still fair representations of the
underlying cluster population and can still be used to probe the
Lx-Tx relation. It is also important to note that the
these flux uncertainties do not apply to the ROSAT observations used
by Markevitch (1998) to determine Lx values for the 30 low
redshift clusters in his
Lx-Tx analysis. Those
observations have exquisite signal to noise, so that the Lxvalues derived from them will be limited only by the absolute
calibration of the instrument.
The fact that we find a Lx-Txrelation consistent with the low redshift value argues against a bias in our selection towards the more luminous tail of the cluster population; for either
We come to very much the same conclusions regarding Lx-Tx evolution as did Vikhlinin et al. (2002). Given that these conclusions provide evidence for significant evolution, contrary to previous analyses, it is important to investigate whether this concordance is genuine or coincidental. Both studies rely on Markevitch (1998) for the low redshift comparison, so let us first consider how our XMM-Newton clusters might appear either too luminous, or too cool, compared to the Markevitch (1998) sample:
Acknowledgements
We thank M. Arnaud for very useful comments concerning the analysis and interpretation of the data. We also thank M. Markevitch and A. Vikhlinin for their assistance. M. Watson is acknowledged for allowing us to use data from the GT observation of IRAS 13224-3809. The EPIC instrument team are thanked for their continued help in improving the calibration knowledge and help in understanding various effects related to the instrument background. We thank the referee, F. Castander for the careful review and comments that helped to improve the interpretations. D.J.B. acknowledges the support of NASA contract NAS8-39073 (CXC). A.K.R. and R.C.N. acknowledge support from the NASA-LTSA program, contract NAG5-11634 and the hospitality of the Durham University Physics department during the summer of 2002. These data were obtained from observations made by the XMM-Newton Observatory. This is an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). The XMM-NewtonProject GT data were provided from a combination of data-rights holders, including the CDS Strasbourg (XMM Science Survey Centre), CEA-Saclay (XMM EPIC PI Team) and the XMM-Newton SOC. AKR acknowledges the Aspen Centre for Physics for hospitality in 2003.
| RX J0337.7 | RX J0505.3 | RX J0847.2 | RX J1120.1 | RX J1325.5 | RX J1334.3 | RX J1354.2 | RX J1701.3 | |
| Centroid RA | 03:37:45 | 05:05:19 | 08:47:10 | 11:20:07 | 13:25:37 | 13:34:20 | 13:54:17 | 17:01:24 |
| Centroid Dec | -25:22:32 | -28:48:50 | +34:48:54 | +43:18:04 | -38:25:44 | +50:31:02 | -02:21:44 | +64:14:12 |
| Cooling flow excised | ||||||||
|
|
2.52 | 2.56 | 3.91 | 5.35 | 3.77 | 4.98 | 3.86 | 4.8 |
|
|
|
|
|
|
|
|
||
|
|
1.91 | 1.97 | 3.89 | 13.7 | 4.2 | 9.47 | 5.3 | 10.2 |
| erg s-1 | ||||||||
| No cooling flow excision | ||||||||
| Tx (keV) | 2.6 | 2.5 | 3.62 | 5.45 | 4.15 | 5.20 | 3.66 | 4.5 |
|
|
|
|
|
|
||||
|
|
1.97 | 2.03 | 4.07 | 14.4 | 4.5 | 9.59 | 5.18 | 11.1 |
| erg s-1 | ||||||||
| Flux (0.5-2) | 4.37 | 5.64 | 7.04 | 24.5 | 8.0 | 14.1 | 9.8 | 24 |
| 10-14cgs |
|
|||||||
| 0.99 | 1.5 | 3.2 | 2.1 | 4.8 | 1.05 | 3.4 | 2.6 | |
| (atom cm-2) | ||||||||
| 0.76 | 0.66 | 0.81 | 0.77 | 0.64 | 0.66 | 0.68 | 0.64 | |
|
|
|
|
||||||
| 145 | 164 | 307 | 209 | 115 | 154 | 248 | 204 | |
| h50-1 |
|
|
fixed | |||||
| Abundance | 0.38 | 0.17 | 0.30 | 0.47 | 0.31 | 0.15 | 0.25 | 0.24 |
| (Z) |
|
|||||||
| z (optical) | 0.577 | 0.51 | 0.56 | 0.60 | 0.445 | 0.62 | 0.551 | 0.45 |
| Normaln. | 1.68 | 2.12 | 2.65 | 9.42 | 2.7 | 5.61 | 4.01 | 5.58 |
| Mekal 10-4 |
|
|
|
|
|
|||
| Radius ('') | 120 | 120 | 120 | 145 | 90 | 120 | 120 | 120 |
| Spect. extract. | ||||||||
| Fractr counts | 0.90 | 0.87 | 0.79 | 0.965 | 0.52 | 0.84 | 0.83 | 0.81 |
| within |
||||||||
| XMM-Newton ID | RA | Dec |
| 2000 | 2000 | |
| Field RX J0337.7-2522 | ||
| XMMU J033737.8-252318 | 03:37:37.8 | -25:23:18.0 |
| XMMU J033743.7-252326 | 03:37:43.7 | -25:23:26.7 |
| XMMU J033742.9-252208 | 03:37:42.9 | -25:22:8.4 |
| XMMU J033745.9-252206 | 03:37:45.9 | -25:22:6.2 |
| XMMU J033747.2-252214 | 03:37:47.2 | -25:22:14.9 |
| Field RX J0505.3-2849 | ||
| XMMU J050512.5-285034 | 05:05:12.5 | -28:50:34.6 |
| XMMU J050517.3-285023 | 05:05:17.3 | -28:50:23.7 |
| XMMU J050522.3-285006 | 05:05:22.3 | -28:50:06.3 |
| XMMU J050510.9-284951 | 05:05:10.9 | -28:49:51.1 |
| Field RX J0847.2+3449 | ||
| XMMU J084711.4+344717 | 08:47:11.4 | 34:47:17.1 |
| XMMU J084714.5+344654 | 08:47:14.5 | 34:46:54.4 |
| XMMU J084707.5+344947 | 08:47:7.5 | 34:49:46.7 |
| XMMU J084709.5+344917 | 08:47:9.5 | 34:49:17.1 |
| Field RX J1120.1+4318 | ||
| XMMU J111959.1+432030 | 11:19:59.1 | 43:20:30.3 |
| XMMU J112001.3+431543 | 11:20:01.3 | 43:15:43.2 |
| XMMU J112004.2+431932 | 11:20:04.2 | 43:19:31.6 |
| XMMU J112008.8+432030 | 11:20:08.8 | 43:20:30.3 |
| XMMU J112009.6+432056 | 11:20:09.6 | 43:20:56.4 |
| XMMU J112014.4+431932 | 11:20:14.4 | 43:19:31.6 |
| XMMU J112015.0+432009 | 11:20:15.0 | 43:20:08.5 |
| Field RX J1334.3+5030 | ||
| XMMU J133426.3+503247 | 13:34:26.3 | 50:32:46.8 |
| XMMU J133410.8+503118 | 13:34:10.8 | 50:31:17.6 |
| XMMU J133415.6+503030 | 13:34:15.6 | 50:30:29.7 |
| XMMU J133416.3+503115 | 13:34:16.3 | 50:31:15.4 |
| XMMU J133430.2+503238 | 13:34:30.2 | 50:32:38.0 |
| XMMU J133428.9+503141 | 13:34:28.9 | 50:31:41.5 |
| Field RX J1354.2-0222 | ||
| XMMU J135414.8-022031 | 13:54:14.8 | -02:20:31.7 |