A&A 418, 1035-1043 (2004)
DOI: 10.1051/0004-6361:20035718
C. M. Walmsley1 - D. R. Flower2 - G. Pineau des Forêts3,4
1 - INAF, Osservatorio Astrofisico di Arcetri,
Largo Enrico Fermi 5, 50125 Firenze, Italy
2 -
Physics Department, The University,
Durham DH1 3LE, UK
3 -
IAS, Université de Paris-Sud, 92405 Orsay Cedex, France
4 - LUTH, Observatoire de Paris, 92195 Meudon Cedex, France
Received 20 November 2003 / Accepted 9 February 2004
Abstract
We have carried out calculations of ionization
equilibrium and deuterium fractionation for conditions
appropriate to a completely depleted, low mass pre-protostellar
core, where
heavy elements such as C, N, and O have vanished from the gas
phase and are incorporated in ice mantles frozen on dust grain
surfaces. We put particular emphasis on the interpretation of
recent observations of H2D+ towards the centre of the
prestellar core L 1544 (Caselli et al. 2003) and also
compute the ambipolar diffusion timescale. We
consider explicitly the ortho and para forms of H2,
H3+, and H2D+. Our results
show that the ionization degree under such conditions depends
sensitively on the grain size distribution or, more precisely,
on the mean grain surface area per hydrogen nucleus. Depending
upon this parameter and upon density, the major ion may be
H+, H3+, or D3+. We show
that the abundance of ortho-H2D+ observed towards L 1544
can be explained satisfactorily in terms of a complete
depletion model and that this species is, as a consequence,
an important tracer of the kinematics of prestellar cores.
Key words: submillimeter - molecular processes - radio lines: ISM
An additional
result from recent observational studies of prestellar
cores is that depletion of molecular species on to dust grain surfaces
is also a marker of relatively evolved cores (i.e. close to the
pivotal state) with high central densities and column densities
(e.g. Caselli et al. 2002; Tafalla et al. 2002).
Tafalla et al.
show that CO becomes depleted by at least a factor of 10, relative to
its canonical abundance, above densities of
![]() cm-3.
CS shows similar behaviour, whereas nitrogen
containing species such as NH3 and N2H+ have abundances which
are either constant or (in the case of ammonia) increase somewhat
in the high density gas surrounding the dust emission peak.
Their interpretation of these observations is that molecular nitrogen
(N2), which
is the source of the observed NH3 and N2H+, is sufficiently
volatile to remain in the gas phase at densities of order 105cm-3 (essentially because of spot heating of the grain surfaces
by cosmic rays), whereas CO (the source of carbon for most C-containing
species) is not.
cm-3.
CS shows similar behaviour, whereas nitrogen
containing species such as NH3 and N2H+ have abundances which
are either constant or (in the case of ammonia) increase somewhat
in the high density gas surrounding the dust emission peak.
Their interpretation of these observations is that molecular nitrogen
(N2), which
is the source of the observed NH3 and N2H+, is sufficiently
volatile to remain in the gas phase at densities of order 105cm-3 (essentially because of spot heating of the grain surfaces
by cosmic rays), whereas CO (the source of carbon for most C-containing
species) is not.
What happens at still higher densities? It seems likely that, at sufficiently high densities, all species containing heavy elements will condense out. The difference in sublimation energies for CO and N2 is not great (e.g. Bergin & Langer 1997) and thus one might expect N2 and other N-containing species to disappear from the gas phase at densities only somewhat higher (or dust temperature slightly lower) than found for CO. Whilst it is true that the laboratory experiments may not accurately simulate interstellar ice surfaces, it seems probable that N2 disappears from the gas phase at densities above 106 cm-3.
In fact, the densities inferred from mm dust continuum emission in
several objects are of order 106 cm-3 and there is
some evidence for "holes'' in the N2H+ distribution at densities
above
![]() cm-3. For example, Bergin et al. (2002)
find a flattening of the N2H+ column density distribution in
B68 which could be interpreted as being due to an absence of N2 towards the dust peak. Belloche (2002) finds a "N2H+ hole''
around the peak of the Class 0 source IRAM04191, which is
most easily interpreted in terms of N2 condensing out at the
highest densities in the prestellar core. Last, but not
least, Caselli et al. (2003, in what follows CvTCB)
have detected compact emission
(2000 AU in size) in the
110-111 H2D+ line towards the
dust emission peak of L 1544.
This latter discovery is significant in view of the fact that CvTCB
infer an abundance of order 10-9 relative to H2.
Estimates of the ionization degree in L 1544 (Caselli et al. 2002)
are of order
cm-3. For example, Bergin et al. (2002)
find a flattening of the N2H+ column density distribution in
B68 which could be interpreted as being due to an absence of N2 towards the dust peak. Belloche (2002) finds a "N2H+ hole''
around the peak of the Class 0 source IRAM04191, which is
most easily interpreted in terms of N2 condensing out at the
highest densities in the prestellar core. Last, but not
least, Caselli et al. (2003, in what follows CvTCB)
have detected compact emission
(2000 AU in size) in the
110-111 H2D+ line towards the
dust emission peak of L 1544.
This latter discovery is significant in view of the fact that CvTCB
infer an abundance of order 10-9 relative to H2.
Estimates of the ionization degree in L 1544 (Caselli et al. 2002)
are of order
![]() .
Taken together, these results
imply that H2D+(and hence probably H3+) is a major ion.
It seems likely that this can be the case only if ions containing
heavy elements, such as N2H+ and HCO+ are absent, which in
turn can be true only if the heavy element content of the gas has
condensed on to grain surfaces. If this is the case,
one must rely on species lacking heavy elements
(such as H2D+) to trace the kinematics of the high density
nucleus of the pre-protostellar core. Also, it becomes relevant
to establish the ionization degree and other
physical parameters of a region where species containing heavy elements
have condensed out.
.
Taken together, these results
imply that H2D+(and hence probably H3+) is a major ion.
It seems likely that this can be the case only if ions containing
heavy elements, such as N2H+ and HCO+ are absent, which in
turn can be true only if the heavy element content of the gas has
condensed on to grain surfaces. If this is the case,
one must rely on species lacking heavy elements
(such as H2D+) to trace the kinematics of the high density
nucleus of the pre-protostellar core. Also, it becomes relevant
to establish the ionization degree and other
physical parameters of a region where species containing heavy elements
have condensed out.
In this paper, we study some of the consequences of complete depletion in an isolated, low mass prestellar core. In particular, we compute the ionization degree and its dependence upon physical parameters such as the gas density and the grain size. We consider in detail deuterium fractionation in these conditions and try to explain the observed H2D+ (or, more precisely, the ortho-H2D+) abundance in objects such as L 1544. In Sect. 2, we discuss the model assumptions and, in Sect. 3, we summarize the results. Then, in Sect. 4, we consider some of the implications of our calculations and in Sect. 5, we briefly summarize our conclusions. Some preliminary results of our study have been presented elsewhere (Walmsley et al. 2004).
Our model derives from the work of Flower et al. (2003) and Flower & Pineau des Forêts (2003). The time-dependent chemical rate equations are solved numerically for a situation in which heavy elements have condensed out on to dust grain surfaces. As in the case of the primordial gas, the only significant gas-phase species are compounds containing the elements H, D and He. An important role is played by the grains which influence the charge distribution (ions, charged grains, and electrons) and enable the formation of H2 and HD. Apart from these latter two processes, we neglect surface chemistry in the present study. We discuss below our assumptions concerning reaction rate coefficients.
First, we consider briefly what is implied by the statement that
"no heavy elements are present in the gas phase''.
For the purpose of the present study, this means in essence that ions
such as H3+, produced as a consequence of cosmic ray ionization
of molecular hydrogen, are destroyed by dissociative recombination
or recombination on grain surfaces, rather than by transferring a proton
to species such as CO and N2 which have larger proton affinities
than H2.
Assuming a rate coefficient ke for dissociative recombination
of H3+ with electrons of
![]() cm3 s-1(McCall et al. 2002, extrapolated to 10 K with a T-0.52dependence: see Appendix A) and a rate coefficient for proton transfer
reactions
between H3+ and species X such as CO or N2 of the order of the Langevin value,
cm3 s-1(McCall et al. 2002, extrapolated to 10 K with a T-0.52dependence: see Appendix A) and a rate coefficient for proton transfer
reactions
between H3+ and species X such as CO or N2 of the order of the Langevin value,
![]() cm3 s-1, the condition for
"complete depletion'' is [X]
cm3 s-1, the condition for
"complete depletion'' is [X]
![]() ,
where
the square brackets denote a fractional abundance; this implies that,
for example, the CO abundance [CO] in the "complete depletion
limit'' should be less than 400[e], or
roughly
,
where
the square brackets denote a fractional abundance; this implies that,
for example, the CO abundance [CO] in the "complete depletion
limit'' should be less than 400[e], or
roughly
![]() in cores such as L 1544,
where
in cores such as L 1544,
where
![]() .
Thus, the calculations reported here will be relevant when species
such as CO have abundances much less than
10-6.
.
Thus, the calculations reported here will be relevant when species
such as CO have abundances much less than
10-6.
In what follows, we report the steady-state conditions predicted by our
calculations. The timescales to reach chemical equilibrium
are somewhat shorter than the dynamical timescales in cores such as
L 1544. The free-fall time is approximately
![]() y for a density
of 106 cm-3;
but, when magnetic fields are present, the collapse time is about an
order of magnitude larger (see Ciolek & Basu 2000; Aikawa et al. 2003).
As shown below, the equilibrium timescale for the entire
chemistry is
roughly 105 y, although ionization equilibrium (with a characteristic
time
y for a density
of 106 cm-3;
but, when magnetic fields are present, the collapse time is about an
order of magnitude larger (see Ciolek & Basu 2000; Aikawa et al. 2003).
As shown below, the equilibrium timescale for the entire
chemistry is
roughly 105 y, although ionization equilibrium (with a characteristic
time
![]() ,
which is of the order of a few years)
is reached much more rapidly.
We conclude that the steady-state assumption is a valid
first approximation but that some of our results may need
to be reconsidered in the light of their time dependence.
,
which is of the order of a few years)
is reached much more rapidly.
We conclude that the steady-state assumption is a valid
first approximation but that some of our results may need
to be reconsidered in the light of their time dependence.
Recombination of ions with electrons on negatively charged grain surfaces is important because, if the available grain surface area is large enough, this process can dominate the destruction of ions such as H3+. Recombination on grains is certainly the main destruction mechanism for protons, which recombine only slowly (radiatively) with electrons in the gas phase, and hence our results depend on the surface area of negatively charged grains. Accordingly, we have considered carefully the distribution of grain charge, adopting the rate coefficients of FPdesF. We assumed that H2 and HD form on grain surfaces, at rates which scale with the total grain surface area.
A key role is played by the ortho/para ratio of molecular hydrogen, which is expected to be much higher than in LTE (see the discussion of Le Bourlot 1991); this has consequences for the ortho/para ratios of species such as H2D+ (see Gerlich et al. 2002, hereafter GHR; Pagani et al. 1992), which become enhanced roughly in proportion to that of H2. Also important in this context are the spin selection rules for ortho-para conversion, discussed, for example, by Uy et al. (1997).
Caution has to be exercised when using the data of Uy et al. (1997). These authors considered conditions in which the ortho and para forms are statistically populated, i.e. in proportion to their nuclear spin statistical weights, (2I + 1). This situation obtains at temperatures and densities much higher than those considered here. In prestellar cores, only the low-lying states of the ortho and para species are significantly populated. Under these circumstances, the statistical weights of the rotational levels, (2J + 1), must be taken explicitly into account. When compiling the rate coefficients for reactions involving the ortho and para forms of H2, H2+, H3+, and H2D+, we made the simplifying assumption that only the lowest rotational level is populated in each case and treated the corresponding ortho and para forms as distinct species, which interconvert through chemical reactions. The complete set of reactions included in the model and their rate coefficients are given in Appendix A.
In the limit of complete depletion, deuterium fractionation occurs mainly in the reactions
Even in the
absence of heavy elements, there are several processes which
limit deuterium substitution in species such as H3+.
For example, it has been known for a long time
that dissociative recombination with electrons,
at a rate
![]() ,
competes with deuterium enrichment in H2D+, for example
(Watson 1978). It is also clear that recombination of H2D+, D2H+ and D3+ on grain surfaces can have a similar effect, and so models
with a large grain surface area tend to have moderate
D-fractionation. The relative importance of these two processes is
roughly the same for D-fractionation and for ion neutralization:
in models where the D-fractionation is limited
by recombination on grain surfaces, the degree of ionization
is limited by the same process.
,
competes with deuterium enrichment in H2D+, for example
(Watson 1978). It is also clear that recombination of H2D+, D2H+ and D3+ on grain surfaces can have a similar effect, and so models
with a large grain surface area tend to have moderate
D-fractionation. The relative importance of these two processes is
roughly the same for D-fractionation and for ion neutralization:
in models where the D-fractionation is limited
by recombination on grain surfaces, the degree of ionization
is limited by the same process.
D-fractionation in an ion such as H2D+ is determined also by the transfer of the deuterium to the higher members of the chain, D2H+ and D3+. Thus reactions 2 and 3 restrict the fractionation in H2D+ and D2H+, respectively. As we shall see below, the effect of these reactions is to limit ratios such as [H2D+]/[H3+] and [D2H+]/[H2D+] to values of the order of unity.
GHR pointed out that ortho-H2 can restrict deuterium fractionation because the reaction between ortho-H2 and ortho-H2D+ is exothermic and believed to be fast. Depending on internal excitation, this process may also be important for D2H+. We find that the reaction with ortho-H2 is not usually dominant but is significant because the abundance of ortho-H2 is high.
The ratio of the H2D+ and H3+ abundances
is given approximately by:
The code described by Flower et al. (2003)
has been used to calculate the steady-state abundances of the
chemical species, Xi.
The program integrates the coupled differential equations
![\begin{displaymath}\frac{\rm d}{{\rm d}t}~ n({\rm X}_{i}) = f[n({\rm X}_{i}),T,t]
\end{displaymath}](/articles/aa/full/2004/18/aa0718/img31.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig1.eps} \end{figure}](/articles/aa/full/2004/18/aa0718/Timg33.gif) |
Figure 1:
Sample result for our reference model (
|
In Fig. 1, we show the results of a sample
calculation in which, initially, the hydrogen and deuterium
are in molecular form, with an elemental abundance ratio
![]() .
The initial ortho/para H2 ratio was
.
The initial ortho/para H2 ratio was
![]() ,
the equilibrium value at the gas kinetic
temperature T = 10 K (assumed constant).
We find that the time required to reach steady state
for all species is of
the order of 105 y (almost independent of number
density). However, as noted above, the
time to attain
ionization equilibrium (a few years) is much shorter than that required to
attain
equilibrium between ortho- and para-H2 (the longest chemical timescale).
Atomic
hydrogen and deuterium are intermediate,
reflecting the timescale for the formation
of H2 and HD on grains.
,
the equilibrium value at the gas kinetic
temperature T = 10 K (assumed constant).
We find that the time required to reach steady state
for all species is of
the order of 105 y (almost independent of number
density). However, as noted above, the
time to attain
ionization equilibrium (a few years) is much shorter than that required to
attain
equilibrium between ortho- and para-H2 (the longest chemical timescale).
Atomic
hydrogen and deuterium are intermediate,
reflecting the timescale for the formation
of H2 and HD on grains.
The time characterizing chemical steady state
is comparable with the
free-fall time,
![]() ,
at the lowest density
(
,
at the lowest density
(
![]() cm-3) and is an order of magnitude
larger than
cm-3) and is an order of magnitude
larger than
![]() at the highest density
(
at the highest density
(![]() =
=
![]() cm-3) considered.
However, magnetic support to the cloud increases the
time for core formation and, in practice, the timescale for
chemical equilibrium is likely to be comparable with that for
contraction and collapse of
the protostellar core.
cm-3) considered.
However, magnetic support to the cloud increases the
time for core formation and, in practice, the timescale for
chemical equilibrium is likely to be comparable with that for
contraction and collapse of
the protostellar core.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig2.eps}\end{figure}](/articles/aa/full/2004/18/aa0718/Timg46.gif) |
Figure 2:
Abundances of major ions and electrons in our
standard model ( |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig3.eps}\end{figure}](/articles/aa/full/2004/18/aa0718/Timg47.gif) |
Figure 3: Ortho/para ratios of H2 (multiplied by 104), H3+, and H2D+ as functions of density for our reference model (cf. Fig. 2). The approximate expression of Gerlich et al. (2002) for H2D+ is shown for comparison. |
In Fig. 2 are plotted the fractional abundances of
the principal ions and of the electrons as functions of
![]() ;
the results of computations of
ortho/para ratios for the same model are presented in Fig. 3
and will be discussed in Sect. 3.4 below.
At the lowest density considered, n(H2) =
105 cm-3, H+ is the major ion and the removal of
molecular ions by dissociative recombination is significant.
H+, on the other hand, is removed by recombination on grain
surfaces. As n(H2) increases, recombination on grains
dominates dissociative recombination for the molecular ions.
H+ becomes a relatively minor species at high
density.
;
the results of computations of
ortho/para ratios for the same model are presented in Fig. 3
and will be discussed in Sect. 3.4 below.
At the lowest density considered, n(H2) =
105 cm-3, H+ is the major ion and the removal of
molecular ions by dissociative recombination is significant.
H+, on the other hand, is removed by recombination on grain
surfaces. As n(H2) increases, recombination on grains
dominates dissociative recombination for the molecular ions.
H+ becomes a relatively minor species at high
density.
The balance between the various deuterated forms of H3+ is determined approximately by Eq. (4) and its analogues for [D2H+]/[H2D+] and [D3+]/[D2H+]. At densities below 106 cm-3, the dissociative recombination term ke [e] is dominant in the denominator of the right hand side of Eq. (4), whereas, at higher densities, the term due to the reaction with HD becomes more important and results in [H2D+]/[H3+] (and [D2H+]/[H2D+]) being close to unity. On the other hand, D3+ cannot be destroyed by HD and becomes the dominant ion.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig5.eps}\end{figure}](/articles/aa/full/2004/18/aa0718/Timg50.gif) |
Figure 5:
The free electron abundance computed as a
function of density for grain sizes between
0.025 and 0.2 |
In Fig. 5, the free electron abundance,
n(e)/
![]() ,
computed as a function of
density, is compared with the relationship of McKee (1989),
,
computed as a function of
density, is compared with the relationship of McKee (1989),
![]() ,
which is often used
in discussions of core evolution. It may be seen that our model generally
predicts lower degrees of ionization. We find that n(e)/
,
which is often used
in discussions of core evolution. It may be seen that our model generally
predicts lower degrees of ionization. We find that n(e)/
![]() varies approximately as
varies approximately as
![]() between
between
![]() and
and
![]() cm-3.
As already noted, the degree of ionization of the gas is sensitive
to the assumed grain size, owing to the importance of the recombination
of ions with electrons on grain surfaces. The fraction
of electrons attached to
grains remains small for all the grain sizes considered here:
the ratio of negatively charged grains to free electrons attains 0.20 for
for
cm-3.
As already noted, the degree of ionization of the gas is sensitive
to the assumed grain size, owing to the importance of the recombination
of ions with electrons on grain surfaces. The fraction
of electrons attached to
grains remains small for all the grain sizes considered here:
the ratio of negatively charged grains to free electrons attains 0.20 for
for
![]()
![]() m and
m and
![]() cm-3. However, we
note that this ratio becomes larger for smaller grain sizes, becoming
cm-3. However, we
note that this ratio becomes larger for smaller grain sizes, becoming ![]() 1 for
1 for
![]()
![]() m. The fraction of grains which is neutral
decreases from 0.68 for
m. The fraction of grains which is neutral
decreases from 0.68 for
![]()
![]() m to 0.20 for
m to 0.20 for
![]()
![]() m and for
m and for
![]() cm-3 (but this ratio is
insensitive to the gas density).
The fraction of positively charged grains
is always negligible.
cm-3 (but this ratio is
insensitive to the gas density).
The fraction of positively charged grains
is always negligible.
The ambipolar diffusion timescale,
![]() ,
depends
on the ion abundance, ni/nn,
the rate coefficient for momentum transfer between the ions and
the neutrals (essentially H2),
,
depends
on the ion abundance, ni/nn,
the rate coefficient for momentum transfer between the ions and
the neutrals (essentially H2),
![]() cm3 s-1, and the masses mi and mn of the charged and neutral
collision partners. We have taken
cm3 s-1, and the masses mi and mn of the charged and neutral
collision partners. We have taken
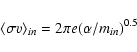
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig6.eps} %
\end{figure}](/articles/aa/full/2004/18/aa0718/Timg64.gif) |
Figure 6:
Ratio of ambipolar diffusion time
|
Figure 3 shows that the ortho/para ratios
considered here are relatively insensitive to density.
For molecular hydrogen, we derive a
steady-state ortho/para
ratio of approximately
![]() for the conditions in the nucleus of
L 1544, and this value is reflected in
the H2D+ ortho/para ratio, as shown by GHR.
In fact, we find that the H2D+ ortho/para ratio
predicted by Eq. (7) of GHR is
a good approximation to our numerical
results.
for the conditions in the nucleus of
L 1544, and this value is reflected in
the H2D+ ortho/para ratio, as shown by GHR.
In fact, we find that the H2D+ ortho/para ratio
predicted by Eq. (7) of GHR is
a good approximation to our numerical
results.
The expression of
Le Bourlot (1991) for ortho/para H2 was derived
for different conditions (lower density and high abundances of
molecular ions such as HCO+) and is not a good approximation
in the conditions that we have considered.
In our situation, the ortho/para H2 ratio is given approximately
by
![]() ,
where
,
where
![]() represents the sum of the number densities of ions such as
H+ and H3+ which convert ortho- to para-H2 through proton
transfer reactions, with a rate coefficient for ortho to para conversion
represents the sum of the number densities of ions such as
H+ and H3+ which convert ortho- to para-H2 through proton
transfer reactions, with a rate coefficient for ortho to para conversion
![]() which is of order 10-10 cm-3 s-1.
which is of order 10-10 cm-3 s-1.
The ortho/para H2D+ ratio has a flat dependence on density, reflecting the behaviour of ortho/para H2. The ortho forms of both H2D+ and H3+ are produced mainly in reactions of the para forms with ortho-H2 and so their high ortho/para ratios are attributable to the relatively high ortho-H2 abundance; Fig. 7 illustrates this point. Because the ortho/para H2 ratio is not thermalized under the conditions which we consider, the ortho/para H2D+ and H3+ ratios are not thermalized either. It follows that measurements of the ortho/para H3+ ratio should not be used to infer a temperature.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig7.eps}\end{figure}](/articles/aa/full/2004/18/aa0718/Timg69.gif) |
Figure 7:
Ortho/para ratios of H3+ and
H2D+ as
functions of the molecular hydrogen ortho/para ratio.
The conditions are those of our reference model:
n(H2) = 106 cm-3, T = 10 K,
|
The basic question that we wish to answer
is whether the ortho-H2D+ emission observed in L 1544 can be reproduced by a model
which assumes complete heavy element depletion.
The abundance of ortho-H2D+
relative to H2 observed towards the peak of L 1544 is
![]() according to CvTCB.
In Fig. 8 are shown the computed values of
[ortho-H2D+]/[H2] as a function of density for various assumed grain
sizes. There is a tendency for [ortho-H2D+]/[H2] to decrease
with increasing density, owing to the fact that deuteration proceeds
further down the chain (towards D3+)
at high density. Our results are within a factor of 2 of the observed peak ortho-H2D+ abundance, for grain radii
below 0.1
according to CvTCB.
In Fig. 8 are shown the computed values of
[ortho-H2D+]/[H2] as a function of density for various assumed grain
sizes. There is a tendency for [ortho-H2D+]/[H2] to decrease
with increasing density, owing to the fact that deuteration proceeds
further down the chain (towards D3+)
at high density. Our results are within a factor of 2 of the observed peak ortho-H2D+ abundance, for grain radii
below 0.1 ![]() m.
Given the observational uncertainties, this level of agreement might
be considered satisfactory. It is also significant that computations
for a = 0.01
m.
Given the observational uncertainties, this level of agreement might
be considered satisfactory. It is also significant that computations
for a = 0.01 ![]() m show that the computed ortho-H2D+ abundance
decreases for all values of
n(H2) relative to the results in Fig. 8 for
a = 0.025
m show that the computed ortho-H2D+ abundance
decreases for all values of
n(H2) relative to the results in Fig. 8 for
a = 0.025 ![]() m, and thus
grain radii in the range 0.025-0.05
m, and thus
grain radii in the range 0.025-0.05 ![]() m maximize the
ortho-H2D+ abundance.
We note that the "observed'' abundance
assumes a rate of collisional excitation of
H2D+, a temperature, and a density distribution, of which
the latter two are controversial (see, for example, Galli et al. 2002).
Higher angular resolution studies of the mm-submm continuum
are needed for further progress.
m maximize the
ortho-H2D+ abundance.
We note that the "observed'' abundance
assumes a rate of collisional excitation of
H2D+, a temperature, and a density distribution, of which
the latter two are controversial (see, for example, Galli et al. 2002).
Higher angular resolution studies of the mm-submm continuum
are needed for further progress.
One result from our study is that a relatively high rate of cosmic ray ionization is required in the nucleus of L 1544 to account for the observed ortho-H2D+ emission; this implies the penetration of low energy (100 MeV) cosmic rays into the high density core. Cosmic ray fluxes higher than assumed here would enhance the computed ortho-H2D+ abundance; but to a higher flux would correspond an increased rate of heat input to the gas and temperatures in excess of those observed in NH3 and other tracers.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig8.eps}\end{figure}](/articles/aa/full/2004/18/aa0718/Timg71.gif) |
Figure 8:
The computed ortho-H2D+ abundance from our reference
model (T = 10 K and
|
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0718fig9.eps}\end{figure}](/articles/aa/full/2004/18/aa0718/Timg72.gif) |
Figure 9: Atomic H (full lines) and atomic D (broken lines) densities for four values of the grain radius (increasing from bottom to top) for densities between 105 and 107 cm-3. |
The grain size distribution in prestellar cores is not known. It depends on
the timescales for grain coagulation and mantle accretion, relative to the
dynamical
and chemical timescales. In view of this uncertainty, we compared the
results of computations assuming
a unique grain radius with the corresponding calculations assuming a MRN
power-law size distribution; we retained the same value of the grain
surface area per H-nucleus,
![]() ,
in both cases.
In calculations with a unique value of
,
in both cases.
In calculations with a unique value of ![]() ,
,
![]() (
(![]() m)) cm2.
When a power law dependence
m)) cm2.
When a power law dependence
![]() is adopted, providing the exponent r > 3 (MRN derived r =
3.5),
the lower limit to the radius essentially determines the grain surface
area. When r =
3.5, the lower limit to
is adopted, providing the exponent r > 3 (MRN derived r =
3.5),
the lower limit to the radius essentially determines the grain surface
area. When r =
3.5, the lower limit to ![]() is 600 Å for
is 600 Å for
![]() cm2.
We found that the results of calculations with the same value of grain
surface area per H-nucleus were quantitatively similar for the cases of a
unique grain radius and a MRN power-law size distribution.
cm2.
We found that the results of calculations with the same value of grain
surface area per H-nucleus were quantitatively similar for the cases of a
unique grain radius and a MRN power-law size distribution.
As shown above, the detection of H2D+ in L 1544 by CvTCB
can be explained if
![]()
![]() m or, equivalently,
if the grain surface area per H-nucleus is
at least
m or, equivalently,
if the grain surface area per H-nucleus is
at least
![]() cm2, which
is close to the value for grains in diffuse clouds.
This conclusion is consistent
with deductions which have been made from the mm-infrared extinction curve
in prestellar regions: Bianchi et
al. (2003) found that the ratio of mm to NIR dust absorption is
marginally larger in prestellar environments than in diffuse clouds; it is
also consistent with the simulations of Ossenkopf & Henning (1994).
cm2, which
is close to the value for grains in diffuse clouds.
This conclusion is consistent
with deductions which have been made from the mm-infrared extinction curve
in prestellar regions: Bianchi et
al. (2003) found that the ratio of mm to NIR dust absorption is
marginally larger in prestellar environments than in diffuse clouds; it is
also consistent with the simulations of Ossenkopf & Henning (1994).
Under conditions of complete heavy element depletion, the thickness of the
grain mantle is expected to
be roughly 40 percent of the grain radius, or 400 Å for 0.1 ![]() m grains. Then,
45 percent of the grain mass is in the refractory core and 55 percent
in the ice mantle. A MRN size distribution yields an ice
mantle
260 Å thick, independent of the grain radius: see Appendix B.
m grains. Then,
45 percent of the grain mass is in the refractory core and 55 percent
in the ice mantle. A MRN size distribution yields an ice
mantle
260 Å thick, independent of the grain radius: see Appendix B.
Unfortunately, the
101-000 transition to the ground
state of para-H2D+ (at 1.37 THz) will be
difficult to excite at the temperatures of prestellar cores and
may be observable only in absorption towards a
background continuum source. On the other hand, H3+ has
no allowed submm transitions and is best observed in the NIR
at 3.5 ![]() m in absorption towards background sources
(McCall et al. 1999).
It has been assumed that the H3+ which has been observed exists
in regions whose composition is similar to that of
"normal'' interstellar molecular clouds and, furthermore, that
the ortho/para forms are in LTE. In our view, both of these
assumptions may prove to be invalid.
Observations of H2D+ and the other members of the
family may help to shed light on this issue.
m in absorption towards background sources
(McCall et al. 1999).
It has been assumed that the H3+ which has been observed exists
in regions whose composition is similar to that of
"normal'' interstellar molecular clouds and, furthermore, that
the ortho/para forms are in LTE. In our view, both of these
assumptions may prove to be invalid.
Observations of H2D+ and the other members of the
family may help to shed light on this issue.
Our results can be compared with those of Roberts et al. (2003) who
carried out a time dependent calculation of the chemistry in a prestellar
core with density
![]() cm-3 including freeze-out. They
found, as do we, that D3+ can be the most abundant ion, though
their results suggest that H3+ becomes the major ion when all
heavy species freeze out; this may be attributable to a different
way of dealing with grain neutralization of ions.
cm-3 including freeze-out. They
found, as do we, that D3+ can be the most abundant ion, though
their results suggest that H3+ becomes the major ion when all
heavy species freeze out; this may be attributable to a different
way of dealing with grain neutralization of ions.
Further progress in this area will depend on our capacity to sample
transitions other than the the
110-111 line of H2D+. H3+ and
D3+ do not have permanent dipole moments, and hence their detection is
feasible only in absorption in the near infrared.
Our calculations suggest that searches for D3+ should be directed
towards regions
where high heavy element depletion is believed
to have occurred. Searches for
emission in low-lying transitions of D2H+ should also be made: the
abundance of D2H+ in conditions of complete depletion is predicted to
be comparable to that of H2D+. Under conditions of LTE at temperature
T, the relative populations of the lowest ortho (000) and para
(101) levels of D2H+ would be
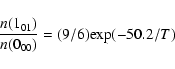
Acknowledgements
It is a pleasure to thank Evelyne Roueff and Eric Herbst for informative and helpful discussions, Paola Caselli for her comments on the text, and the referee, Ted Bergin, for a constructive and thought-provoking report. CMW thanks the Ecole Normale Supérieure in Paris for hospitality during a stay when part of the work described here was carried out as well as the Max Planck Institute in Bonn for hospitality on diverse occasions.
In this Appendix are specified the reactions included and the rate coefficients adopted in our chemical model.
Protons have nuclear spin I = 1/2 and are fermions. The ortho and para forms of H2, H2+, H3+ and H2D+ have been treated as distinct species. Ortho- and para-H2 were assumed to form hot, on grains, in the ratio 3:1 of their nuclear spin statistical weights. Subsequent proton-exchange reactions interconvert the ortho and para forms. Such reactions were assumed to involve only the rotational ground states of the ortho and para modifications, and the corresponding rate coefficients take account of the relative statistical weights (2I+1)(2J+1) of the products and reactants.
Deuteration of H3+ in reactions with HD may be viewed as proton transfer (from H3+ to HD) or deuteron-proton exchange; we allowed for both viewpoints in our reaction set. Rate coefficients for dissociative recombination, with electrons in the gas phase or on negatively charged grains, were assumed to be the same for the ortho and para forms of the recombining ion.
We note that deuterons have nuclear spin I = 1 and are bosons. Multiply deuterated species have ortho and para forms. In the present study, we have not attempted to allow for the consequences of Bose-Einstein statistics when evaluating the rates of reactions involving multiply-deuterated species.
| Reaction | |||
| H + H
|
0.25 | ||
| H + H
|
0.75 | ||
| H + D
|
1.00 | ||
| H + crp
|
0.46 | ||
| He + crp
|
0.50 | ||
| H2(p) + crp
|
0.04 | ||
| H2(o) + crp
|
0.04 | ||
| H2(p) + crp
|
1.50 | ||
| H2(o) + crp
|
1.50 | ||
| H2(p) + crp
|
0.96 | ||
| H2(o) + crp
|
0.96 | ||
| H+ + H2(o)
|
2.20(-10) | 0.00 | 0.0 |
| H3+(p) + H2(o)
|
4.40(-10) | 0.00 | 0.0 |
| H3+(o) + H2(o)
|
1.10(-10) | 0.00 | 0.0 |
| H+ + H2(p)
|
1.98(-09) | 0.00 | 170.5 |
| H3+(p) + H2(p)
|
1.98(-09) | 0.00 | 203.4 |
| H3+(o) + H2(p)
|
1.98(-09) | 0.00 | 137.6 |
| H2+(o) + H2(o)
|
1.05(-09) | 0.00 | 0.0 |
| H2+(o) + H2(o)
|
1.05(-09) | 0.00 | 0.0 |
| H2+(p) + H2(o)
|
1.05(-09) | 0.00 | 0.0 |
| H2+(p) + H2(o)
|
1.05(-09) | 0.00 | 0.0 |
| H2+(o) + H2(p)
|
1.05(-09) | 0.00 | 0.0 |
| H2+(o) + H2(p)
|
1.05(-09) | 0.00 | 0.0 |
| H2+(p) + H2(p)
|
2.10(-09) | 0.00 | 0.0 |
| He+ + H2(p)
|
1.10(-13) | -0.24 | 0.0 |
| He+ + H2(o)
|
1.10(-13) | -0.24 | 0.0 |
| H+ + e-
|
3.61(-12) | -0.75 | 0.0 |
| H2+(p) + e-
|
1.60(-08) | -0.43 | 0.0 |
| H2+(o) + e-
|
1.60(-08) | -0.43 | 0.0 |
| He+ + e-
|
4.50(-12) | -0.67 | 0.0 |
| H3+(p) + e-
|
5.10(-08) | -0.52 | 0.0 |
| H3+(o) + e-
|
5.10(-08) | -0.52 | 0.0 |
| H3+(p) + e-
|
1.13(-08) | -0.52 | 0.0 |
| H3+(p) + e-
|
0.57(-08) | -0.52 | 0.0 |
| H3+(o) + e-
|
1.70(-08) | -0.52 | 0.0 |
| D + crp
|
0.46 | ||
| HD + crp
|
0.02 | ||
| HD + crp
|
0.02 | ||
| HD + crp
|
1.50 | ||
| HD + crp
|
0.96 | ||
| D+ + H
|
1.00(-09) | 0.00 | 0.0 |
| H+ + D
|
1.00(-09) | 0.00 | 41.0 |
| D+ + H2(p)
|
2.10(-09) | 0.00 | 0.0 |
| D+ + H2(o)
|
2.10(-09) | 0.00 | 0.0 |
| H+ + HD
|
1.00(-09) | 0.00 | 464.0 |
| H+ + HD
|
1.00(-09) | 0.00 | 634.5 |
| HD+ + H2(p)
|
5.25(-10) | 0.00 | 0.0 |
| HD+ + H2(p)
|
5.25(-10) | 0.00 | 0.0 |
| HD+ + H2(o)
|
5.25(-10) | 0.00 | 0.0 |
| HD+ + H2(o)
|
5.25(-10) | 0.00 | 0.0 |
| HD+ + H2(p)
|
1.05(-09) | 0.00 | 0.0 |
| HD+ + H2(o)
|
5.25(-09) | 0.00 | 0.0 |
| HD+ + H2(o)
|
5.25(-09) | 0.00 | 0.0 |
| H2+(p) + HD
|
5.25(-10) | 0.00 | 0.0 |
| H2+(p) + HD
|
5.25(-10) | 0.00 | 0.0 |
| H2+(o) + HD
|
5.25(-10) | 0.00 | 0.0 |
| H2+(o) + HD
|
5.25(-10) | 0.00 | 0.0 |
| H2+(p) + HD
|
1.05(-09) | 0.00 | 0.0 |
| H2+(o) + HD
|
5.25(-10) | 0.00 | 0.0 |
| H2+(o) + HD
|
5.25(-10) | 0.00 | 0.0 |
| H3+(p) + D
|
0.66(-09) | 0.00 | 0.0 |
| H3+(p) + D
|
0.33(-09) | 0.00 | 0.0 |
| H3+(o) + D
|
1.00(-09) | 0.00 | 0.0 |
| H2D+(p) + H
|
1.00(-09) | 0.00 | 632.0 |
| H2D+(o) + H
|
0.50(-09) | 0.00 | 578.4 |
| H2D+(o) + H
|
0.50(-09) | 0.00 | 545.5 |
| H3+(p) + HD
|
1.17(-10) | 0.00 | 0.0 |
| H3+(p) + HD
|
1.17(-10) | 0.00 | 0.0 |
| H3+(p) + HD
|
5.83(-11) | 0.00 | 0.0 |
| H3+(p) + HD
|
5.83(-11) | 0.00 | 25.0 |
| H3+(o) + HD
|
1.75(-10) | 0.00 | 0.0 |
| H3+(o) + HD
|
1.75(-10) | 0.00 | 0.0 |
| H2D+(p) + H2(o)
|
1.98(-09) | 0.00 | 0.0 |
| H2D+(o) + H2(p)
|
1.98(-09) | 0.00 | 84.0 |
| H2D+(o) + H2(o)
|
2.44(-11) | 0.00 | 0.0 |
| H2D+(p) + H2(p)
|
1.98(-09) | 0.00 | 257.0 |
| H2D+(p) + H2(p)
|
1.40(-10) | 0.00 | 232.0 |
| H2D+(p) + H2(o)
|
0.70(-10) | 0.00 | 61.5 |
| H2D+(p) + H2(o)
|
0.70(-10) | 0.00 | 94.4 |
| H2D+(o) + H2(p)
|
1.40(-10) | 0.00 | 145.5 |
| H2D+(o) + H2(o)
|
0.70(-10) | 0.00 | 0.0 |
| H2D+(o) + H2(o)
|
0.70(-10) | 0.00 | 8.0 |
| He+ + HD
|
5.50(-14) | -0.24 | 0.0 |
| He+ + HD
|
5.50(-14) | -0.24 | 0.0 |
| D+ + e-
|
3.61(-12) | -0.75 | 0.0 |
| HD+ + e-
|
3.40(-09) | -0.40 | 0.0 |
| H2D+(p) + e-
|
4.96(-08) | -0.52 | 0.0 |
| H2D+(o) + e-
|
4.96(-08) | -0.52 | 0.0 |
| H2D+(p) + e-
|
1.36(-08) | -0.52 | 0.0 |
| H2D+(o) + e-
|
1.36(-08) | -0.52 | 0.0 |
| H2D+(p) + e-
|
4.76(-09) | -0.52 | 0.0 |
| H2D+(o) + e-
|
4.76(-09) | -0.52 | 0.0 |
| D+ + H
|
3.90(-19) | 1.80 | 0.0 |
| H+ + D
|
3.90(-19) | 1.80 | 0.0 |
| H2+(p) + D
|
7.00(-18) | 1.80 | 0.0 |
| HD+ + H
|
1.20(-17) | 1.80 | 0.0 |
| HD+ + H
|
6.40(-10) | 0.00 | 0.0 |
| H2+(p) + D
|
6.40(-10) | 0.00 | 0.0 |
| HD+ + H
|
1.00(-09) | 0.00 | 154.0 |
| H2+(p) + D
|
1.00(-09) | 0.00 | 0.0 |
| D2 + crp
|
0.04 | ||
| D2 + crp
|
1.50 | ||
| D2 + crp
|
0.96 | ||
| H+ + D2
|
2.10(-09) | 0.00 | 491.0 |
| D+ + HD
|
1.00(-09) | 0.00 | 0.0 |
| D2+ + H2(p)
|
1.05(-09) | 0.00 | 0.0 |
| D2+ + H2(o)
|
1.05(-09) | 0.00 | 0.0 |
| D2+ + H2(p)
|
1.05(-09) | 0.00 | 0.0 |
| D2+ + H2(o)
|
1.05(-09) | 0.00 | 0.0 |
| H2+(p) + D2
|
1.05(-09) | 0.00 | 0.0 |
| H2+(o) + D2
|
1.05(-09) | 0.00 | 0.0 |
| H2+(p) + D2
|
1.05(-09) | 0.00 | 0.0 |
| H2+(o) + D2
|
1.05(-09) | 0.00 | 0.0 |
| HD+ + HD
|
5.25(-10) | 0.00 | 0.0 |
| HD+ + HD
|
5.25(-10) | 0.00 | 0.0 |
| HD+ + HD
|
1.05(-09) | 0.00 | 0.0 |
| H2D+(p) + D
|
1.00(-09) | 0.00 | 0.0 |
| H2D+(o) + D
|
1.00(-09) | 0.00 | 0.0 |
| HD2+ + H
|
1.00(-09) | 0.00 | 600.0 |
| HD2+ + H
|
1.00(-09) | 0.00 | 513.5 |
| H3+(o) + D2
|
3.50(-10) | 0.00 | 0.0 |
| H3+(o) + D2
|
3.50(-10) | 0.00 | 0.0 |
| H3+(p) + D2
|
2.33(-10) | 0.00 | 0.0 |
| H3+(p) + D2
|
1.17(-10) | 0.00 | 0.0 |
| H3+(p) + D2
|
2.33(-10) | 0.00 | 0.0 |
| H3+(p) + D2
|
1.17(-10) | 0.00 | 0.0 |
| H2D+(p) + HD
|
2.60(-10) | 0.00 | 0.0 |
| H2D+(o) + HD
|
2.60(-10) | 0.00 | 0.0 |
| H2D+(o) + HD
|
1.30(-10) | 0.00 | 108.0 |
| H2D+(o) + HD
|
1.30(-10) | 0.00 | 75.0 |
| H2D+(p) + HD
|
2.60(-10) | 0.00 | 161.5 |
| HD2+ + H2(p)
|
1.00(-10) | 0.00 | 190.0 |
| HD2+ + H2(p)
|
1.00(-10) | 0.00 | 277.0 |
| HD2+ + H2(o)
|
1.00(-10) | 0.00 | 106.0 |
| HD2+ + H2(o)
|
1.00(-10) | 0.00 | 20.1 |
| HD2+ + H2(p)
|
2.00(-10) | 0.00 | 320.0 |
| HD2+ + H2(o)
|
1.00(-10) | 0.00 | 149.5 |
| HD2+ + H2(o)
|
1.00(-10) | 0.00 | 182.4 |
| He+ + D2
|
1.10(-13) | -0.24 | 0.0 |
| He+ + D2
|
2.50(-14) | 0.00 | 0.0 |
| D2+ + e-
|
3.40(-09) | -0.40 | 0.0 |
| HD2+ + e-
|
4.96(-08) | -0.52 | 0.0 |
| HD2+ + e-
|
1.36(-08) | -0.52 | 0.0 |
| HD2+ + e-
|
4.76(-09) | -0.52 | 0.0 |
| D2+ + H
|
6.40(-10) | 0.00 | 0.0 |
| HD+ + D
|
6.40(-10) | 0.00 | 0.0 |
| HD+ + D
|
1.00(-09) | 0.00 | 0.0 |
| D2+ + H
|
1.00(-09) | 0.00 | 472.0 |
| D2+ + D
|
6.40(-10) | 0.00 | 0.0 |
| D2+ + HD
|
1.05(-09) | 0.00 | 0.0 |
| D2+ + HD
|
1.05(-09) | 0.00 | 0.0 |
| HD+ + D2
|
1.05(-09) | 0.00 | 0.0 |
| HD+ + D2
|
1.05(-09) | 0.00 | 0.0 |
| HD2+ + D
|
1.00(-09) | 0.00 | 0.0 |
| D3+ + H
|
1.00(-09) | 0.00 | 655.0 |
| HD2+ + HD
|
1.00(-10) | 0.00 | 0.0 |
| HD2+ + HD
|
1.00(-10) | 0.00 | 0.0 |
| HD2+ + HD
|
1.00(-10) | 0.00 | 110.0 |
| HD2+ + HD
|
1.00(-10) | 0.00 | 196.5 |
| H2D+(p) + D2
|
8.50(-10) | 0.00 | 0.0 |
| H2D+(o) + D2
|
8.50(-10) | 0.00 | 0.0 |
| H2D+(p) + D2
|
8.50(-10) | 0.00 | 0.0 |
| H2D+(o) + D2
|
8.50(-10) | 0.00 | 0.0 |
| D3+ + H2(p)
|
1.50(-09) | 0.00 | 352.0 |
| D3+ + H2(o)
|
1.50(-09) | 0.00 | 268.0 |
| D3+ + H2(p)
|
1.50(-09) | 0.00 | 241.0 |
| D3+ + H2(o)
|
1.50(-09) | 0.00 | 70.5 |
| D3+ + e-
|
2.03(-08) | -0.50 | 0.0 |
| D3+ + e-
|
6.75(-09) | -0.50 | 0.0 |
| D2+ + D2
|
2.10(-09) | 0.00 | 0.0 |
| D3+ + HD
|
1.50(-09) | 0.00 | 161.5 |
| g0 + secpho
|
0.63(08) | ||
| g- + secpho
|
0.41(09) | ||
| g0 + e-
|
6.90(-05) | 0.50 | 0.0 |
| g- + H+
|
1.60(-06) | 0.50 | 0.0 |
| g- + H3+(p)
|
3.07(-07) | 0.50 | 0.0 |
| g- + H3+(p)
|
1.54(-07) | 0.50 | 0.0 |
| g- + H3+(o)
|
4.61(-07) | 0.50 | 0.0 |
| g- + H3+(p)
|
4.61(-07) | 0.50 | 0.0 |
| g- + H3+(o)
|
4.61(-07) | 0.50 | 0.0 |
| g- + He+
|
8.00(-07) | 0.50 | 0.0 |
| g0 + H+
|
1.60(-06) | 0.50 | 0.0 |
| g0 + H3+(p)
|
3.07(-07) | 0.50 | 0.0 |
| g0 + H3+(p)
|
1.54(-07) | 0.50 | 0.0 |
| g0 + H3+(o)
|
4.61(-07) | 0.50 | 0.0 |
| g0 + H3+(p)
|
4.61(-07) | 0.50 | 0.0 |
| g0 + H3+(o)
|
4.61(-07) | 0.50 | 0.0 |
| g0 + He+
|
8.00(-07) | 0.50 | 0.0 |
| g+ + e-
|
6.90(-05) | 0.50 | 0.0 |
| g- + D+
|
1.13(-06) | 0.50 | 0.0 |
| g- + H2D+(p)
|
1.33(-07) | 0.50 | 0.0 |
| g- + H2D+(p)
|
2.66(-07) | 0.50 | 0.0 |
| g- + H2D+(o)
|
1.33(-07) | 0.50 | 0.0 |
| g- + H2D+(o)
|
2.66(-07) | 0.50 | 0.0 |
| g- + H2D+(p)
|
3.99(-07) | 0.50 | 0.0 |
| g- + H2D+(o)
|
3.99(-07) | 0.50 | 0.0 |
| g0 + D+
|
1.13(-06) | 0.50 | 0.0 |
| g0 + H2D+(p)
|
1.33(-07) | 0.50 | 0.0 |
| g0 + H2D+(p)
|
2.66(-07) | 0.50 | 0.0 |
| g0 + H2D+(o)
|
1.33(-07) | 0.50 | 0.0 |
| g0 + H2D+(o)
|
2.66(-07) | 0.50 | 0.0 |
| g0 + H2D+(p)
|
3.99(-07) | 0.50 | 0.0 |
| g0 + H2D+(o)
|
3.99(-07) | 0.50 | 0.0 |
| g- + HD2+
|
2.38(-07) | 0.50 | 0.0 |
| g- + HD2+
|
1.19(-07) | 0.50 | 0.0 |
| g- + HD2+
|
3.57(-07) | 0.50 | 0.0 |
| g0 + HD2+
|
2.38(-07) | 0.50 | 0.0 |
| g0 + HD2+
|
1.19(-07) | 0.50 | 0.0 |
| g0 + HD2+
|
3.57(-07) | 0.50 | 0.0 |
| g- + D3+
|
3.26(-07) | 0.50 | 0.0 |
| g- + D3+
|
3.26(-07) | 0.50 | 0.0 |
| g0 + D3+
|
3.26(-07) | 0.50 | 0.0 |
| g0 + D3+
|
3.26(-07) | 0.50 | 0.0 |
In this Appendix, we derive estimates of the ice-mantle thickness in completely depleted cores. We follow the approach of FPdesF.
Following FPdesF, we assume the refractory cores to be composed of
silicates (in practice, olivine, MgFeSiO4) or graphite. The mass of the
cores, per unit volume of gas, is
![]() ,
where the summation extends over the elements X, and
M denotes the elemental mass.
We define
,
where the summation extends over the elements X, and
M denotes the elemental mass.
We define
![]() through the relation
through the relation
![]() ,
and
,
and
![]() ,
which corresponds to a fraction of 0.0056 by mass
relative to the gas-phase H and He.
,
which corresponds to a fraction of 0.0056 by mass
relative to the gas-phase H and He.
Assuming that all elements heavier than He are in the grain cores or frozen
in the mantles, the total dust-to-gas mass density ratio is 0.0125, and
the mass per unit volume of the gas of the ice in the mantle, is
![]() ,
where
,
where
![]() .
.
The volume ![]() of a grain ice mantle is determined by the relation
of a grain ice mantle is determined by the relation
| (B.1) |
| (B.2) |
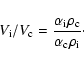 |
(B.3) |
This analysis can be generalized to the case of a MRN power-law
size distribution, using the formalism of Le Bourlot et al. (1995). If the
lower limit of the size distribution is taken to be am = 0.01 ![]() m (and the upper limit is aM = 0.3
m (and the upper limit is aM = 0.3 ![]() m), then the thickness
m), then the thickness ![]() of the mantle is obtained by solving the equation
of the mantle is obtained by solving the equation
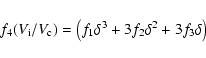 |
(B.4) |
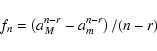 |
(B.5) |