A&A 418, 225-233 (2004)
DOI: 10.1051/0004-6361:20040023
Blue loops of intermediate mass stars
II. Metallicity and blue loops
H. Y. Xu1 - Y. Li1,2
1 - National Astronomical Observatories/Yunnan Observatory, PO Box 110, 650011 Kunming, PR China
2 -
Joint Laboratory for Optical Astronomy, Chinese Academy of Sciences, PR China
Received 12 May 2003 / Accepted 19 December 2003
Abstract
Based on the results of the blue loop formation for
models of solar-like metallicity, we have explored the blue
loop evolution of metal-poor stars. Three series of models
with a wide range of metallicity and the initial helium abundance
were calculated. An important parameter,
 ,
defined as the
envelope convection mass divided by the total envelope mass at the
bottom of the RGB, was introduced as a criterion to determine the
formation of the blue loop. We have found that the low-Z models
will develop extensive blue loops when
,
defined as the
envelope convection mass divided by the total envelope mass at the
bottom of the RGB, was introduced as a criterion to determine the
formation of the blue loop. We have found that the low-Z models
will develop extensive blue loops when
 is lower than a
critical value
is lower than a
critical value
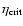 .
The physical explanation for this
result could be as follows. Lower Z reduces the envelope opacity
and leads to a hotter stellar envelope and a bluer RGB. Thus the
model will have a smaller
.
The physical explanation for this
result could be as follows. Lower Z reduces the envelope opacity
and leads to a hotter stellar envelope and a bluer RGB. Thus the
model will have a smaller
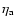 at the top and an even smaller
at the top and an even smaller
 at the bottom of the RGB. When
at the bottom of the RGB. When
 is lower than
the critical value
is lower than
the critical value
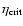 ,
the envelope is
radiation-dominated. Under this condition and the constraint of
the virial theorem, the response of the star to the increase of
the stellar luminosity is to contract to increase the thermal
conductivity coefficient in the stellar envelope and to form a
blue loop. Compared with the high-Z models, we have confirmed that
the development of convection in the stellar envelope is a crucial
factor to determine the formation of the blue loop, but the low-Zmodels reach low
,
the envelope is
radiation-dominated. Under this condition and the constraint of
the virial theorem, the response of the star to the increase of
the stellar luminosity is to contract to increase the thermal
conductivity coefficient in the stellar envelope and to form a
blue loop. Compared with the high-Z models, we have confirmed that
the development of convection in the stellar envelope is a crucial
factor to determine the formation of the blue loop, but the low-Zmodels reach low
 values in a different way from the
high-Z models, in which the modulation of the nuclear reaction
rates by higher 14N abundance in the H-burning shell is
responsible for the stars to get small
values in a different way from the
high-Z models, in which the modulation of the nuclear reaction
rates by higher 14N abundance in the H-burning shell is
responsible for the stars to get small
 values. It has
been found that
values. It has
been found that
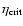 depends not only on the stellar
mass, but also on metallicity and the initial helium
abundance. Our numerical results show that
depends not only on the stellar
mass, but also on metallicity and the initial helium
abundance. Our numerical results show that
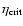 decreases with Z while slowly increases with Y.
decreases with Z while slowly increases with Y.
Key words: stars: evolution -
stars: interiors -
stars: Hertzsprung-Russell (HR) and C-M diagrams
The formation and extension of the blue loop is closely related to
many physical conditions in the evolution of intermediate mass
stars. In a previous paper (Xu & Li 2004, hereafter referred to
as Paper I), we have made extensive investigations on the
formation of the blue loop for stellar models of solar-like
composition. We found that the blue loop evolution depends closely
on the development of the envelope convection and nuclear energy
production in the H-burning shell. Here we will pay more attention
to models with different metallicity, especially those metal-poor
models that develop very extended blue loops.
Chemical composition is of strong effects on the formation and extension of
the blue loop. There is a general tendency that higher helium abundance with
constant metallicity leads to more extended blue loops (Robertson 1971;
Robertson 1972b; Fricke & Strittmatter 1972). However, the relationship
between the blue loop and the metallicity is more complicated. Previous
investigations based on the stellar models of different Z suggested
that lower metallicity made more extended blue loop
(Hallgren & Cox 1970; Robertson 1971; Robertson 1972b; Castellani et al.
1990; Alongi et al. 1991; Schaller et al. 1992; Pols et al. 1998). Due to the variation of the initial X, Y, and Z in most of the models and the
incomplete coverage of Z values, the detailed relationship of the blue
loop to the metallicity cannot be found clearly and straightforwardly from
the literature. Two sequences of models with Y=0.27 in Bono et al. (2000,
hereafter BY27) and with X=0.70 in Alcock & Paczynski (1978, hereafter
AX70) are helpful for understanding the dependance of the blue loop on Z,
because they have adequate coverage of Z values.
Although the two sequences used different opacity tables and
other input physics, they showed a similar trend of the blue loop evolution,
i.e., when the stellar mass is higher than about
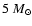 ,
the
extension of the blue loop decreases as Z increases from 0.004 to 0.01,
and increases as Z increases from 0.01 to 0.02, while when the stellar
mass is lower than
,
the
extension of the blue loop decreases as Z increases from 0.004 to 0.01,
and increases as Z increases from 0.01 to 0.02, while when the stellar
mass is lower than
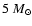 ,
the extension of the blue loop decreases
monotonically as Z increases from 0.004 to 0.02. Dominguez's (1999) models
share similar properties of the blue loop evolution but their choice of Yor X is not constant when Z varies. Early attempts made to determine the
effect of composition on the blue loop showed also other different views
(Hofmeister 1967; Schlesinger 1969; Hallgren & Cox 1970; Harris & Deupree 1976).
,
the extension of the blue loop decreases
monotonically as Z increases from 0.004 to 0.02. Dominguez's (1999) models
share similar properties of the blue loop evolution but their choice of Yor X is not constant when Z varies. Early attempts made to determine the
effect of composition on the blue loop showed also other different views
(Hofmeister 1967; Schlesinger 1969; Hallgren & Cox 1970; Harris & Deupree 1976).
The physical relationship between the metallicity and the blue loop has not
been clearly understood up to now. The location of the hydrogen profile
outside the helium core was sometimes considered as a possible factor
(Robertson 1972a; Stothers & Chin 1968, 1973; Schlesinger 1977; Stothers & Chin 1991). Another possible factor was lower opacity due to lower metallicity, since lower opacity in the radiative envelope could make a star
bluer (Stothers & Chin 1968, 1973; Schlesinger 1977).
Series of evolution models with different Z but constant X or Y are
rare in the literature, but they are desirable for the investigation of the
relationship between the metallicity and the blue loop. In this paper, we
shall investigate the development of the blue loop under different
metallicity, in order to see whether the formation mechanism of the blue
loop for high metallicity models differs from that for low metallicity
models, and how the metallicity affects the formation of the blue
loop.
Physical inputs adopted in our model calculations are similar to those in
Paper I and briefly introduced in Sect. 2. Properties of the evolution
models are discussed in Sect. 3. Comparisons of the evolution models with
different metallicity are given in Sect. 4. Furthermore, we investigate the
structure of the stellar models during the blue loop phase and discuss the
formation mechanism of the blue loop in Sect. 5. Conclusions and discussions
are summarized in Sect. 6.
Physical assumptions and computation methods adopted in the present
investigation were similar to those in Paper I, and here we only give a
brief summary.
The rates of the nuclear reactions were taken from Caughlan & Fowler
(1988). The OPAL opacities G91hz series (Iglesias & Rogers 1996) were used
in the high temperature region and the low temperature opacities were taken
from Alexander & Ferguson (1994). Energy transfer by convection was treated
according to the standard mixing-length theory and the boundaries of the
convection zones were determined by the Schwarzschild criterion (Cox &
Giuli 1968; Huang & Yu 1998). The ratio of the mixing-length to local
pressure scale height, 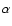 ,
was chosen to be 1.8. Overshooting and
mass loss were ignored. Our revised stellar evolution code was originally
described by Kippenhahn et al. (1967).
,
was chosen to be 1.8. Overshooting and
mass loss were ignored. Our revised stellar evolution code was originally
described by Kippenhahn et al. (1967).
Models with the metal abundance of Z= 0.020, 0.018, 0.016, ... , 0.004 and
the helium abundance of Y= 0.28, 0.26, 0.23 were calculated. For
the considered heavy element abundance, we chose
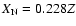 as the initial
nitrogen abundance, which was the sum of the original abundance of 14N
and 12C, and
as the initial
nitrogen abundance, which was the sum of the original abundance of 14N
and 12C, and
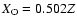 as the initial oxygen abundance. These
choices of the initial abundance were referred to a solar-scaled heavy
element distribution (Anders & Grevesse 1989; Grevesse & Noels 1993).
as the initial oxygen abundance. These
choices of the initial abundance were referred to a solar-scaled heavy
element distribution (Anders & Grevesse 1989; Grevesse & Noels 1993).
CN models and CNO models were described in Paper I. The CN models only
considered the CN cycle in the hydrogen burning process, and the CNO models
were based on an approximation of the CNO bi-cycle (Clayton 1968) and could
reproduce most of the properties of stellar models using the
nuclear-reaction network. All of these models consisted of enough mass zones
and time steps to avoid the numerical inaccuracy.
![\begin{figure}
\par\includegraphics[height=14cm,width=16.2cm,angle=270,clip]{fig1.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg12.gif) |
Figure 1:
Evolutionary tracks of the CN models. Models with Z= 0.004, 0.006, ..., 0.02
are plotted in each panel, among which the models without the blue loop have solid lines and those having the blue loop have other types of lines. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=14cm,width=16.2cm,angle=270,clip]{fig2.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg13.gif) |
Figure 2:
Evolutionary tracks of the CNO models. Models with Z= 0.004, 0.006, ..., 0.02
are plotted in each panel, among which the models without the blue loop have solid lines and those having the blue loop have other types of lines. |
| Open with DEXTER |
We calculated three series of evolution tracks of a
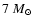 model with
the considered values of helium abundance. Both the CN and the CNO models
were calculated, and their evolution tracks are shown in Figs. 1 and 2,
respectively. The three series of the CN models (see Fig. 1) show a common
behavior of the blue loop with different Z, and the lower Z always
results in more extended blue loops (Hallgren & Cox 1970; Robertson
1971; Robertson 1972b; Castellani et al. 1990; Alongi et al. 1991; Schaller
et al. 1992). However, the CNO models (see Fig. 2) show that the width of
the blue loop decreases when Z increases from 0.004 to 0.01, and turns to
increase when Z increases from 0.01 to 0.02, which is similar to the trend
in BY27 and AX70. We regard this result as the actual relationship between Z and the blue loop, because the CNO models are more accurate than the CN models. Comparing Figs. 1 and 2, we can see that the CN and CNO models develop the blue loops when Z is low enough. Similar results can be found in the literature (e.g. Bono et al. 2000). This implies that the low opacity
due to low Z in the stellar envelope may be a chief factor to determine
the blue loop evolution (Hallgren & Cox 1970; Robertson 1971; Robertson
1972b; Castellani et al. 1990; Alongi et al. 1991; Schaller et al. 1992;
Pols et al. 1998). The CNO models develop blue loops again when Z is high
enough while the CN models do not. This result indicates that the formation
of the blue loop in the low-Z models may be different from that in the
high-Z models. The helium abundance has a less but still noticeable effect on the
development of the blue loop, and higher Y facilitates in the low Zlimit and hampers in the high Z limit the development of the blue loop
(Robertson 1971; Robertson 1972b; Fricke & Strittmatter 1972). This result
indicates again that the lower opacity due to the higher helium in the low-Zmodels can affect the blue loop evolution (Schlesinger 1977).
model with
the considered values of helium abundance. Both the CN and the CNO models
were calculated, and their evolution tracks are shown in Figs. 1 and 2,
respectively. The three series of the CN models (see Fig. 1) show a common
behavior of the blue loop with different Z, and the lower Z always
results in more extended blue loops (Hallgren & Cox 1970; Robertson
1971; Robertson 1972b; Castellani et al. 1990; Alongi et al. 1991; Schaller
et al. 1992). However, the CNO models (see Fig. 2) show that the width of
the blue loop decreases when Z increases from 0.004 to 0.01, and turns to
increase when Z increases from 0.01 to 0.02, which is similar to the trend
in BY27 and AX70. We regard this result as the actual relationship between Z and the blue loop, because the CNO models are more accurate than the CN models. Comparing Figs. 1 and 2, we can see that the CN and CNO models develop the blue loops when Z is low enough. Similar results can be found in the literature (e.g. Bono et al. 2000). This implies that the low opacity
due to low Z in the stellar envelope may be a chief factor to determine
the blue loop evolution (Hallgren & Cox 1970; Robertson 1971; Robertson
1972b; Castellani et al. 1990; Alongi et al. 1991; Schaller et al. 1992;
Pols et al. 1998). The CNO models develop blue loops again when Z is high
enough while the CN models do not. This result indicates that the formation
of the blue loop in the low-Z models may be different from that in the
high-Z models. The helium abundance has a less but still noticeable effect on the
development of the blue loop, and higher Y facilitates in the low Zlimit and hampers in the high Z limit the development of the blue loop
(Robertson 1971; Robertson 1972b; Fricke & Strittmatter 1972). This result
indicates again that the lower opacity due to the higher helium in the low-Zmodels can affect the blue loop evolution (Schlesinger 1977).
Table 1:
The values of 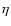 at the three critical position.
at the three critical position.
![\begin{figure}
\par\includegraphics[height=13.8cm,width=7.9cm,angle=270,clip]{fig3.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg19.gif) |
Figure 3:
Evolutionary tracks of the
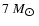 stars with Y=0.28, during the
early phase of the central He burning. The crosses, asterisks, and circles
respectively represent the moment of the top of the RGB (a), the bottom of
the RGB (c), and the envelope convection decreases maximally (min).
stars with Y=0.28, during the
early phase of the central He burning. The crosses, asterisks, and circles
respectively represent the moment of the top of the RGB (a), the bottom of
the RGB (c), and the envelope convection decreases maximally (min). |
| Open with DEXTER |
Some critical values during the He-core burning stage are listed in Table 1.
An important parameter, 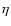 ,
is defined as the ratio of the envelope
convection mass to the total envelope mass (see Paper I):
,
is defined as the ratio of the envelope
convection mass to the total envelope mass (see Paper I):
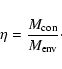 |
(1) |
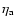 and
and
 represent respectively the value of
represent respectively the value of 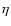 at the
top and the bottom of the red-giant branch (RGB), and
at the
top and the bottom of the red-giant branch (RGB), and
 is the
smallest value of
is the
smallest value of 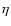 when the envelope convection decreases mostly
after the ignition of the He core. If there is a blue loop,
when the envelope convection decreases mostly
after the ignition of the He core. If there is a blue loop,
 will be zero, which means that the envelope is almost wholly in the
radiative equilibrium. We mark these points (a, c, and min) in Fig. 3
to clearly indicate their position in the HR diagram (HRD), which is a
magnified part of the evolution tracks of the models with Y=0.28 in Fig. 2. Figure 3 shows a typical series of evolution tracks of the CNO models
during the early stage of the central He-burning phase, in which the three
markers correspond to the position of
will be zero, which means that the envelope is almost wholly in the
radiative equilibrium. We mark these points (a, c, and min) in Fig. 3
to clearly indicate their position in the HR diagram (HRD), which is a
magnified part of the evolution tracks of the models with Y=0.28 in Fig. 2. Figure 3 shows a typical series of evolution tracks of the CNO models
during the early stage of the central He-burning phase, in which the three
markers correspond to the position of
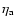 (cross),
(cross),
 (asterisk) and
(asterisk) and
 (circle) respectively in the Table 1.
(circle) respectively in the Table 1.
The value of
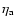 is an important parameter for the formation of the
blue loop, which describes how deep the envelope convection can penetrate
downward just after the He-core ignition. It can be found from Table 1 and
Fig. 3 that a model with a lower Z value gets a smaller
is an important parameter for the formation of the
blue loop, which describes how deep the envelope convection can penetrate
downward just after the He-core ignition. It can be found from Table 1 and
Fig. 3 that a model with a lower Z value gets a smaller
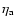 value,
although its luminosity is higher. The reasons for this effect comes from two
aspects. A model with a lower Z value is always brighter than that with a
higher Z value in the main sequence and forms a larger He core. At the
moment of the central He ignition, the lower Z model has a hotter He core
and a hotter envelope. The larger and hotter He core produces a higher
luminosity at the top of the RGB, while the hotter envelope makes the energy
transfer more efficient and then the underdevelopment of the envelope
convection to get a smaller value of
value,
although its luminosity is higher. The reasons for this effect comes from two
aspects. A model with a lower Z value is always brighter than that with a
higher Z value in the main sequence and forms a larger He core. At the
moment of the central He ignition, the lower Z model has a hotter He core
and a hotter envelope. The larger and hotter He core produces a higher
luminosity at the top of the RGB, while the hotter envelope makes the energy
transfer more efficient and then the underdevelopment of the envelope
convection to get a smaller value of
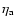 .
It can be seen in Fig. 3
that a smaller Z leads to a bluer and brighter position a (see the
crosses).
.
It can be seen in Fig. 3
that a smaller Z leads to a bluer and brighter position a (see the
crosses).
It can be found from Table 1 that all the evolution tracks with
the blue loops are of comparably low
 at the bottom of
the RGB. This confirms the conclusion in Paper I that a blue loop
will be formed if
at the bottom of
the RGB. This confirms the conclusion in Paper I that a blue loop
will be formed if
 is smaller than a critical value
is smaller than a critical value
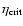 .
In the CNO models,
.
In the CNO models,
 increases before about
Z=0.012 and then decreases after Z=0.012 when Z increases
from 0.004 to 0.02, corresponding to the formation of the blue
loops at the high and low Z limit for these series of models. It
can be found in the series of Y=0.28 models, however, that a
blue loop is formed when
increases before about
Z=0.012 and then decreases after Z=0.012 when Z increases
from 0.004 to 0.02, corresponding to the formation of the blue
loops at the high and low Z limit for these series of models. It
can be found in the series of Y=0.28 models, however, that a
blue loop is formed when
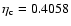 in the model of
Z=0.006, and that there is no blue loop even if
in the model of
Z=0.006, and that there is no blue loop even if
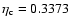 in
the model of Z=0.018. This result indicates that
in
the model of Z=0.018. This result indicates that
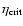 depends not only on the stellar mass (see Paper I), but also on
the metallicity. Low Z reduces the opacity of the stellar envelope, and the critical value of
depends not only on the stellar mass (see Paper I), but also on
the metallicity. Low Z reduces the opacity of the stellar envelope, and the critical value of
 has therefore to vary. From Table 1 it may be approximately
concluded that
has therefore to vary. From Table 1 it may be approximately
concluded that
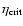 increases as Z decreases, which implies that
low-Z models are more available for the formation of the blue loop.
Comparing the models with the blue loops at constant Z, we find that
increases as Z decreases, which implies that
low-Z models are more available for the formation of the blue loop.
Comparing the models with the blue loops at constant Z, we find that
 increases when Y increases, which implies that
increases when Y increases, which implies that
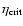 increases with Y and that models with higher helium abundance are more
suitable for the formation of the blue loop. This result shows the common
behavior of the blue loop that higher Y makes more extended blue loops
because of lower opacities (Fricke & Strittmatter 1972; Bono et al. 2000).
increases with Y and that models with higher helium abundance are more
suitable for the formation of the blue loop. This result shows the common
behavior of the blue loop that higher Y makes more extended blue loops
because of lower opacities (Fricke & Strittmatter 1972; Bono et al. 2000).
We find in Fig. 3 that the asterisks are arranged in an arched shape, which
is unlike the behavior of the crosses. The distance between each set of the
crosses and asterisks is lengthened when Z increases, and the luminosity
difference from a to c,
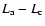 is also enlarged when Z increases.
This is the effect of
is also enlarged when Z increases.
This is the effect of 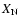 on the RGB evolution as we have discussed in
Paper I. It is obvious that a small value of
on the RGB evolution as we have discussed in
Paper I. It is obvious that a small value of
 can result in blue
loop evolution, but how a star can reach a small
can result in blue
loop evolution, but how a star can reach a small
 may be different
between the metal-poor and metal-rich models, and our research will be
focused on this question.
may be different
between the metal-poor and metal-rich models, and our research will be
focused on this question.
On the other hand, the variation of
 in Table 1 shows that the
transition from a fairly large
in Table 1 shows that the
transition from a fairly large
 value (about 0.3) to zero is
quite sudden, which strongly indicates that the envelope convection zone is
very sensitive to the metallicity and will disappear rapidly as soon as the
condition of the formation of the blue loop is satisfied. The circles in
Fig. 3 show that the envelope convection becomes the smallest when the star
evolves to the bluest tip if there is no blue loop. For those tracks with
the blue loops, the position of the circles becomes cooler and fainter as Zincreases, which means that the envelope convection zone vanishes
differently in the models with different Z. This is because the lower Zresults in the lower opacity in the stellar envelope, too.
value (about 0.3) to zero is
quite sudden, which strongly indicates that the envelope convection zone is
very sensitive to the metallicity and will disappear rapidly as soon as the
condition of the formation of the blue loop is satisfied. The circles in
Fig. 3 show that the envelope convection becomes the smallest when the star
evolves to the bluest tip if there is no blue loop. For those tracks with
the blue loops, the position of the circles becomes cooler and fainter as Zincreases, which means that the envelope convection zone vanishes
differently in the models with different Z. This is because the lower Zresults in the lower opacity in the stellar envelope, too.
![\begin{figure}
\par\includegraphics[height=13.6cm,width=7.7cm,angle=270,clip]{fig4.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg24.gif) |
Figure 4:
The nuclear energy generated in the He-core (dashed) and the H-shell(solid) of the CNO model. The position of a, c, and min are marked by the same symbols as in Fig. 3. |
| Open with DEXTER |
Our stellar models may develop the blue loops when Z is low or high
enough, so we separate them into two kinds divided by Z=0.012, around
which
 reaches the largest value in Table 1. This value of Zdepends on the stellar mass, metallicity, etc., and our choice is in
agreement with the results of BY27, AX70 and Dominguez (1999). A typical
low-Z model is chosen to be one of Z=0.004 and a typical high-Z model is
one of Z=0.02. By comparing the properties of the low-Z and high-Z models
we may find how Z affects the blue loop.
reaches the largest value in Table 1. This value of Zdepends on the stellar mass, metallicity, etc., and our choice is in
agreement with the results of BY27, AX70 and Dominguez (1999). A typical
low-Z model is chosen to be one of Z=0.004 and a typical high-Z model is
one of Z=0.02. By comparing the properties of the low-Z and high-Z models
we may find how Z affects the blue loop.
From Fig. 4 we find that the energy generation of the central He core grows
monotonically and that of the H-burning shell experiences a sudden increase
during the early blue loop phase, which corresponds to the
luminosity increase of the blue loop evolution. This result confirms that
the luminosity variation of the blue loop comes from the nuclear energy in
the H-burning shell for both low-Z and high-Z models. It should be pointed
out that the position of the circle, which marks the disappearance of the
envelope convection, is always located at the early ascending branch of the
H-shell nuclear energy evolution in both CNO and CN models with the blue
loops. The low-Z models usually have steep ascending branches of the H-shell
nuclear energy production, and the rapid increase of the H-shell energy
production makes the envelope contracting rapidly to increase the
temperature and thermal conductivity coefficient, thus the envelope
convection decreases rapidly. The rapid increase
of the H-shell energy production in our models is not caused by the
so-called secular instability, because the estimated thermal time-scale is
much shorter than the time considered, and more than 99% of the whole
luminosity is contributed by the nuclear energy.
The nuclear energy variation in the H-burning shell is different
between the low-Z model and the high-Z model. In the low-Z model, the
energy production in the H-burning shell increases steeply in a short time
and afterwards stays at a roughly steady high level for a long time. In
the high-Z model, however, the H-shell energy production increases gradually
with a moderate slope in the whole ascending branch of the blue loop.
The H-shell during the energy increase phase varies in a similar way in the
high-Z and low-Z models from Fig. 5. The central temperature of the H-shell
increases during this period, and this results from the envelope contraction
and controls the nuclear energy production in the H-shell. The density and
pressure of the H-shell decrease correspondingly, because the H-shell will
expand and step out toward lower density and pressure regions. There are also
some differences between these two models in Fig. 5. At the time of the
minimum luminosity, the central temperature of the H-shell in the Z=0.004model is about 6% higher than that in the Z=0.02 model, and the pressure
is 9% larger. There is a steep decrease phase in the pressure and density,
which corresponds to the sharp increase of the H-shell energy production in Fig. 4.
![\begin{figure}
\par\includegraphics[height=16cm,width=7.6cm,angle=270,clip]{fig7.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg27.gif) |
Figure 7:
 in the considered models (Y=0.28) are plotted
against the initial abundance Z and
in the considered models (Y=0.28) are plotted
against the initial abundance Z and 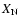 .
The CNO (solid) and
CN models (dashed) are plotted. .
The CNO (solid) and
CN models (dashed) are plotted. |
| Open with DEXTER |
The central status of the low-Z model is quite different from that
of the high-Z model in Fig. 6. Except for a short reverse period,
the central density and pressure decrease in the low-Z model while
increase in the high-Z model. On the other hand, the central
temperature increases during the blue loop phase in both kinds of
models. This difference may come from the fact that the blue loop
evolution takes place in different stages of the central
He-burning process in the low-Z and high-Z models (Kippenhahn &
Weigert 1990 and references therein). During the early stage of
the central He-burning process, the He-burning core expands slowly
and the central density and pressure decrease correspondingly. Our
low-Z model is in this stage when it develops the blue loop,
because the central He abundance is as high as 0.633 at the
beginning of the blue loop. When the helium abundance is low
enough during the late stage of the central He burning, the
stellar core has to contract to maintain the stellar luminosity
still increasing and therefore to increase the pressure and
density. Our high-Z model is in this phase and its central helium
abundance is only 0.257 at the beginning of the blue loop.
The rapid variation of the H-shell in the model of Z=0.004 can affect the
stellar core structure from Figs. 5 and 6. It can be seen that the nuclear
energy generation of the He core is suppressed when the H-shell burning
increases rapidly. We ascribe this effect to the variation of the convective
core. During the early stage of the central He burning, the convective core
is usually larger than the central nuclear reaction region and expands
slowly, therefore convection can bring fresh helium into the nuclear burning
region. But when the H-burning shell is enlarging its nuclear energy
production rapidly, the layer below the H-shell is heated and the core
convection zone stops moving outward or even moves inward. So the nuclear
burning core cannot get fresh helium anymore, and the He-burning core must
contract to raise its pressure and density to maintain the steady state.
This result indicates that the state of the He-core is not completely
independent of the H-shell. In most stages of the central He burning
process, however, the stellar core is indeed not disturbed by the envelope
and H-shell, so we can take it as a good approximation in most cases.
These differences between the models of Z=0.004 and Z=0.02 indicate that
the low-Z and high-Z models develop their blue loops in different ways. The
two models reach small
 in different processes, and we will
investigate this in the next section.
in different processes, and we will
investigate this in the next section.
We have noticed that the metal abundance Z has two main effects on the
blue loop. For low-Z models, lower opacities due to lower Z facilitates
the development of the blue loop according to many previous investigations
(Stothers & Chin 1968; Castellani et al. 1990; Alongi et al. 1991; Schaller
et al. 1992; Bono et al. 2000). Our results show that lower opacity in the
stellar envelope makes the top of the RGB bluer, which leads to a smaller
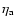 as the envelope convection cannot penetrate inward so deeply. It is very important that a small
as the envelope convection cannot penetrate inward so deeply. It is very important that a small
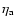 can strongly depress the development
of the envelope convection, and the star will rapidly evolve to the bottom
of the RGB with a fairly small
can strongly depress the development
of the envelope convection, and the star will rapidly evolve to the bottom
of the RGB with a fairly small
 .
Just like the mechanism we have
discussed in Paper I, the envelope will contract rapidly and the star will
develop an extended blue loop when
.
Just like the mechanism we have
discussed in Paper I, the envelope will contract rapidly and the star will
develop an extended blue loop when
 is smaller than the critical
value. For high-Z models, higher 14N abundance due to higher Z in the
H-burning shell makes the H-shell burning more efficient and the "push
effect'' more effective, and the stellar envelop can therefore reach a
larger
is smaller than the critical
value. For high-Z models, higher 14N abundance due to higher Z in the
H-burning shell makes the H-shell burning more efficient and the "push
effect'' more effective, and the stellar envelop can therefore reach a
larger
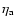 at the top of the RGB and a chemical discontinuity closer
to the shell source, and a smaller
at the top of the RGB and a chemical discontinuity closer
to the shell source, and a smaller
 at the bottom of the RGB in the
subsequent evolution, as we have already discussed in Paper I.
at the bottom of the RGB in the
subsequent evolution, as we have already discussed in Paper I.
![\begin{figure}
\par\includegraphics[height=6.9cm,width=7.1cm,angle=270,clip]{fig...
...
\includegraphics[height=6.9cm,width=7.1cm,angle=270,clip]{fig8b.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg28.gif) |
Figure 8:
Two kinds of models in which the envelope Z is enhanced ( left panel) or
decreased ( right panel). |
| Open with DEXTER |
Taking account of these two effects of metallicity, we can explain the
effects of Z on the blue loop according to Fig. 7. Along with the increase
of Z from 0.004 to about 0.012, the envelope opacity increases to make
 increase also. This postpones the formation of the blue
loop and the width of the blue loop decreases, and
furthermore the blue loop is eventually forbidden. These processes
are all dominated by the envelope opacity, so that
increase also. This postpones the formation of the blue
loop and the width of the blue loop decreases, and
furthermore the blue loop is eventually forbidden. These processes
are all dominated by the envelope opacity, so that
 increases whether it is a CNO or a CN model. With further increase
of Z, the 14N abundance in the CNO models takes effect and
the two kinds of models evolve in different ways. For the CNO models in Fig. 7, when Z increases to 0.012 and
increases whether it is a CNO or a CN model. With further increase
of Z, the 14N abundance in the CNO models takes effect and
the two kinds of models evolve in different ways. For the CNO models in Fig. 7, when Z increases to 0.012 and 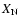 in the
H-shell reaches about 0.008, the 14N abundance in
the H-shell is so high that it makes the "push effect'' strong enough and
in the
H-shell reaches about 0.008, the 14N abundance in
the H-shell is so high that it makes the "push effect'' strong enough and
 decreases gradually to zero, then the blue loop is rebuilt. We
can find a critical value of
decreases gradually to zero, then the blue loop is rebuilt. We
can find a critical value of 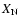 ,
about 0.008 when Z=0.012, above which
the blue loop will be reformed. For the CN models, however, the 14N abundance of the H shell source is very low and cannot take effect for the
considered values of Z. Under the control of increasing envelope opacity,
,
about 0.008 when Z=0.012, above which
the blue loop will be reformed. For the CN models, however, the 14N abundance of the H shell source is very low and cannot take effect for the
considered values of Z. Under the control of increasing envelope opacity,
 increases within the considered parameter range. Figure 7 shows that
increases within the considered parameter range. Figure 7 shows that
 of the CN models can become larger than 0.5 while
of the CN models can become larger than 0.5 while
 of the CNO models only get to about 0.46.
of the CNO models only get to about 0.46.
We verify the two effects of Z on the formation of the blue loop
in Fig. 8. Two kinds of models are constructed, one is the
enhanced-Z model and the other is the decreased-Z model. In the
left panel, the metallicity in the stellar envelope is
artificially increased from 0.004 to 0.01 for one model and from 0.014 to 0.02 for the other. The moment of this treatment is
arranged just after the stars ignite their central helium burning
(also the moment when the envelope convection zone is penetrating
most), and the contaminated region is set in the stellar
envelope beyond the hydrogen profile, to keep the
X-profile unchanged. The solid line shows that the blue loop is
forbidden and the star evolves like the model of Z=0.01, and we
can conclude that the contaminating process to increase the
opacity of the envelope affects the evolution of the star.
The dashed line shows
that the blue loop is not developed and the star evolves like the model of Z=0.014, and the contaminating process has no effect because the 14N abundance in the H-shell is not enlarged to form the blue loop. In the right
panel, the two opposite models with decreasing Z process in the
stellar envelope also show that the star behaves like the model of Z=0.004when its envelope Z decreases from 0.01 to 0.004, and the other star
evolves like the model of Z=0.02 when its envelope Z decreases from 0.02
to 0.014. All of these models indicate that when Z is lower than about 0.012, the envelop Z dominates the evolution of the star, and when Z is higher than 0.012, the 14N abundance in the H-shell dominates the behavior of the star.
By comparing the properties of low-Z and high-Z models, we have explored the
effects of metallicity on the blue loop and put our focus on the formation
of the blue loop in low-Z models. It has been found that lower opacities due
to lower Z in the stellar envelope plays a crucial role in the formation
of the blue loop. Although the star with lower opacity has a larger nuclear
burning core and therefore a brighter luminosity at the top of the RGB, it
has a hotter envelope and a bluer RGB, which effectively depresses the
development of convection in the stellar envelope. When the envelope opacity
is low enough, the stellar envelope will be radiation-dominated at the
bottom of the RGB and its envelope convective ratio
 ,
defined as
the envelope convection mass divided by the total envelope mass, will be
smaller than a critical value
,
defined as
the envelope convection mass divided by the total envelope mass, will be
smaller than a critical value
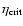 ,
and the star will form a blue
loop in its subsequent evolution.
,
and the star will form a blue
loop in its subsequent evolution.
Comparing the high-Z and low-Z models, we have found that the formation
mechanisms of the blue loops are different from each other. For low-Zmodels, lower metallicity makes the envelope opacity lower, which results in
smaller
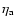 at the top of the RGB and thereafter smaller
at the top of the RGB and thereafter smaller
 at
the bottom of the RGB. For high-Z models, higher Z results in higher 14N abundance and more effective nuclear burning in the H-shell, which
leads to two main effects. One is a larger
at
the bottom of the RGB. For high-Z models, higher Z results in higher 14N abundance and more effective nuclear burning in the H-shell, which
leads to two main effects. One is a larger
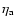 to let the envelope
convection penetrate deeper and to leave an X-profile closer to the shell
source. The other is a stronger "push effect'' to let
to let the envelope
convection penetrate deeper and to leave an X-profile closer to the shell
source. The other is a stronger "push effect'' to let
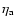 rapidly
decrease to smaller
rapidly
decrease to smaller
 along the descent of the RGB. A blue loop
will be developed when
along the descent of the RGB. A blue loop
will be developed when
 is lower than a critical value
is lower than a critical value
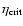 .
Besides, we have found that the low-Z models form their blue
loops in the early stage of the central helium burning, while the high-Zmodels form their blue loops in the late stage of the central helium
burning. This has been identified by comparing the response of the
stellar core to the rapid increase of the stellar luminosity during the
beginning of the blue loop.
.
Besides, we have found that the low-Z models form their blue
loops in the early stage of the central helium burning, while the high-Zmodels form their blue loops in the late stage of the central helium
burning. This has been identified by comparing the response of the
stellar core to the rapid increase of the stellar luminosity during the
beginning of the blue loop.
By comparing the blue loop evolution under different parameters, we have
found that
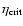 depends not only on the stellar mass (see Paper I), but also on the metallicity. From our numerical results,
depends not only on the stellar mass (see Paper I), but also on the metallicity. From our numerical results,
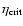 increases as Z decreases, which indicates that low-Z models
form blue loops more easily.
increases as Z decreases, which indicates that low-Z models
form blue loops more easily.
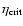 has been found to have a weak dependence on
the initial helium abundance, and
has been found to have a weak dependence on
the initial helium abundance, and
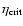 increases with Y. It
should be noticed that the dependence of
increases with Y. It
should be noticed that the dependence of
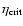 on the stellar mass,
metallicity, and the initial helium may be different for high-Z and low-Zmodels, since the formation mechanisms of their blue loops are different.
on the stellar mass,
metallicity, and the initial helium may be different for high-Z and low-Zmodels, since the formation mechanisms of their blue loops are different.
We have confirmed that the envelope convective ratio at the bottom of the
RGB,
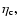 is an essential factor to determine whether a star develops
a blue loop or not. The stellar models with very low or high metallicity are
found to develop blue loops when
is an essential factor to determine whether a star develops
a blue loop or not. The stellar models with very low or high metallicity are
found to develop blue loops when
 is lower than a critical value
is lower than a critical value
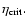 This fact confirms the validity of
This fact confirms the validity of
 as a general
criterion to determine the formation of a blue loop, as soon as the
dependence of
as a general
criterion to determine the formation of a blue loop, as soon as the
dependence of
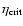 on the stellar mass, metallicity, and the
initial helium abundance is established.
on the stellar mass, metallicity, and the
initial helium abundance is established.
 measures the physical
structure of a stellar envelope just before the blue loop phase, and it
cannot be a result of the blue loop evolution. When
measures the physical
structure of a stellar envelope just before the blue loop phase, and it
cannot be a result of the blue loop evolution. When
 is small
enough, the stellar envelope is radiation-dominated. Under this condition
and the constraint of the virial theorem, the only response of the stellar
envelope to an increase of the stellar luminosity is to contract and to
increase its thermal conductivity coefficient, to transfer the
extra heat flowing through it.
is small
enough, the stellar envelope is radiation-dominated. Under this condition
and the constraint of the virial theorem, the only response of the stellar
envelope to an increase of the stellar luminosity is to contract and to
increase its thermal conductivity coefficient, to transfer the
extra heat flowing through it.
It should be noticed that
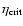 may depend on more
physical ingredients, such as the mass loss through the stellar
wind and between the binary system, overshooting from the
convective core, element diffusion, etc., but the basic physics of
the formation of the blue loop will not be changed. It can be
applied to more complicated situations to analyze the formation of
the blue loop.
may depend on more
physical ingredients, such as the mass loss through the stellar
wind and between the binary system, overshooting from the
convective core, element diffusion, etc., but the basic physics of
the formation of the blue loop will not be changed. It can be
applied to more complicated situations to analyze the formation of
the blue loop.
Acknowledgements
This work is co-sponsored by the NSFC of China through grant
number 19833040 and 10173024, National Key Fundamental Research
Project through grant G1999075405 and G2000078401. The authors
thank the anonymous referee for suggesting to pay attention to
the differences of the triggering of the blue loop between low-Zand high-Z models. We thank R. Q. Huang, S. L. Bi, J. Y. Yang,
and J. H. Guo for helpful discussions.
- Alcock, C., &
Paczynski, B. 1978, ApJ, 223, 244 [NASA ADS] [CrossRef] (AX70)
(In the text)
- Alexander, D. R.,
& Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] (In the text)
- Alongi, M., Bertelli,
G., Bressan, A., & Chiosi, C. 1991, A&A, 244, 95 [NASA ADS] (In the text)
- Anders, E., &
Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [NASA ADS] [CrossRef] (In the text)
- Bono, G., Caputo, F.,
Cassisi, S., et al. 2000, ApJ, 543, 955 [NASA ADS] [CrossRef] (BY27)
(In the text)
- Castellani, V.,
Chieffi, A., & Straniero, O. 1990, ApJS, 74, 463 [NASA ADS] [CrossRef] (In the text)
- Caughlan, G. R.,
& Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40,
283 [NASA ADS] (In the text)
- Clayton, D. D. 1968,
Principles of Stellar Evolution and Nucleosynthesis (US:
McGraw-Hill Inc.)
(In the text)
- Cox, J. P., & Giuli, R.
T. 1968, Principles of Stellar Structure (New York: Gordon and
Breach)
(In the text)
- Dominguez, I.,
Chieffi, A., Limongi, M., & Straniero, O. 1999, ApJ, 524,
226 [NASA ADS] [CrossRef] (In the text)
- Fricke, K. J., &
Strittmatter, P. A. 1972, MNRAS, 156, 129 [NASA ADS] (In the text)
- Grevesse, N., &
Noels, A. 1993, in Origin and Evolution of the Elements, ed. N.
Prantzos, E. Vangioni, & M. Cassé (Cambridge: Cambridge
Univ. Press), 15
(In the text)
- Hallgren, E. L.,
& Cox, J. P. 1970, ApJ, 162, 993 [NASA ADS] [CrossRef] (In the text)
- Harris, G. L., &
Deupree, R. 1976, ApJ, 209, 402 [NASA ADS] [CrossRef] (In the text)
- Hofmeister, E.
1967, Z. Astrophys., 65, 164 [NASA ADS] (In the text)
- Huang, R. Q., & Yu,
K. N. 1998, Stellar Astrophysics (Singapore: Springer-Verlag)
(In the text)
- Iglesias, C. A.,
& Rogers, F. J. 1996, ApJ, 464, 943 [CrossRef] (In the text)
- Kippenhahn,
R., Weigert, A., & Hofmeister, E. 1967, Methods in
Computational Physics, 7 (New York: Academic Press), 129
(In the text)
- Kippenhahn,
R., & Weigert, A. 1990, Stellar Structure and Evolution
(Berlin: Springer)
(In the text)
- Pols, O. R., Schroder, K.
P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS,
298, 525 [NASA ADS] [CrossRef] (In the text)
- Renzini, A., Greggio,
L., & Ritossa, C. 1992, ApJ, 400, 280 [NASA ADS] [CrossRef]
- Robertson, J.
W. 1971, ApJ, 170, 353 [NASA ADS] [CrossRef] (In the text)
- Robertson, J.
W. 1972a, ApJ, 173, 631 [NASA ADS] [CrossRef] (In the text)
- Robertson, J.
W. 1972b, ApJ, 177, 473 [NASA ADS] [CrossRef] (In the text)
- Schaller., G.,
Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96,
269 [NASA ADS] (In the text)
-
Schlesinger, B. M. 1969, ApJ, 158, 1059 [NASA ADS] [CrossRef] (In the text)
-
Schlesinger, B. M. 1977, ApJ, 212, 507 [NASA ADS] [CrossRef] (In the text)
- Stothers, R. B., &
Chin, C. W. 1968, ApJ, 152, 225 [NASA ADS] [CrossRef] (In the text)
- Stothers, R. B., &
Chin, C. W. 1973, ApJ, 175, 555 [NASA ADS] (In the text)
- Stothers, R. B., &
Chin, C. W. 1991, ApJ, 374, 288 [NASA ADS] [CrossRef] (In the text)
- Xu, H. Y., & Li, Y. 2004,
A&A, 418, 213 [EDP Sciences] [NASA ADS] [CrossRef] (Paper I)
(In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[height=14cm,width=16.2cm,angle=270,clip]{fig1.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg12.gif)
![\begin{figure}
\par\includegraphics[height=14cm,width=16.2cm,angle=270,clip]{fig2.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg13.gif)
![\begin{figure}
\par\includegraphics[height=13.8cm,width=7.9cm,angle=270,clip]{fig3.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg19.gif)
![\begin{figure}
\par\includegraphics[height=13.6cm,width=7.7cm,angle=270,clip]{fig4.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg24.gif)
![\begin{figure}
\par\includegraphics[height=7.8cm,width=6.9cm,angle=270,clip]{fig...
...
\includegraphics[height=7.8cm,width=6.9cm,angle=270,clip]{fig5b.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg25.gif)
![\begin{figure}
\par\includegraphics[height=7.8cm,width=6.9cm,angle=270,clip]{fig...
...
\includegraphics[height=7.8cm,width=6.9cm,angle=270,clip]{fig6b.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg26.gif)
![\begin{figure}
\par\includegraphics[height=16cm,width=7.6cm,angle=270,clip]{fig7.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg27.gif)
![\begin{figure}
\par\includegraphics[height=6.9cm,width=7.1cm,angle=270,clip]{fig...
...
\includegraphics[height=6.9cm,width=7.1cm,angle=270,clip]{fig8b.ps}\end{figure}](/articles/aa/full/2004/16/aa3972/Timg28.gif)