- ... form
![[*]](/icons/foot_motif.gif)
- The reason is that in Eq. (6)
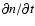 is linearly dependent
on the second derivative
is linearly dependent
on the second derivative
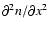 ,
i.e. the coefficient of
,
i.e. the coefficient of
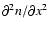 in Eq. (6) does not contain n. Therefore it is seen
from Eq. (15) that only the form
in Eq. (6) does not contain n. Therefore it is seen
from Eq. (15) that only the form
![$j(x)\sim \left [\partial n/\partial x+f(n)\right ]$](/articles/aa/full/2004/14/aah4524/img111.gif) or
or
![$j(x)=g(x)\left [\partial n/\partial x+f(n)\right ]$](/articles/aa/full/2004/14/aah4524/img112.gif) is possible and the proportional
coefficient g(x) has to be independent of n. Furthermore, it can be deduced that the
function f(n) must be taken as
f(n)=n(n+1) due to the fact that when the photon gas reaches
thermal equilibrium we have j(x)=0, hence
is possible and the proportional
coefficient g(x) has to be independent of n. Furthermore, it can be deduced that the
function f(n) must be taken as
f(n)=n(n+1) due to the fact that when the photon gas reaches
thermal equilibrium we have j(x)=0, hence
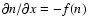 .
On the other hand,
in this case the distribution function is Planckian,
.
On the other hand,
in this case the distribution function is Planckian,
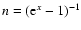 ,
thus
,
thus
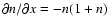 .
Therefore we get
f(n)=n(n+1), and Eq. (16) is
obtained where g(x) is an undetermined coefficient.
.
Therefore we get
f(n)=n(n+1), and Eq. (16) is
obtained where g(x) is an undetermined coefficient.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- The energy density of the
radiation field is given by
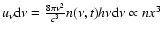 ,
therefore the spectral intensity is expressed by
,
therefore the spectral intensity is expressed by
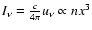 ,
or
,
or
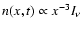 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.