| (1) |
A&A 415, 1167-1176 (2004)
DOI: 10.1051/0004-6361:20031701
F. Robert
Muséum-USM 205, CNRS-UMS 2679 LEME, 61 rue Buffon, 75005 Paris, France
Received 20 June 2003 / Accepted 6 November 2003
Abstract
The treatment proposed to account for the
non-mass-dependent isotopic fractionation effect observed for oxygen
isotopes during the synthesis of ozone (Robert & Camy-Peyret 2001) is
applied to other chemical elements. A numerical treatment to calculate
isotopic reaction rate ratios is proposed. This treatment yields
non-mass-dependent isotopic effects in other chemical elements,
qualitatively similar to those observed in some of the high temperature
minerals found in the carbonaceous meteorites. This treatment may reflect
the numerical consequences of an unrecognized quantum mechanical effect,
linked to a property of chemical reactions involving indistinguishable
isotopes.
Key words: meteoroids - supernovae: general - nucleosynthesis - solar system: formation
Non-mass-dependent isotopic effects (designated in the Cosmochemical literature as "isotopic anomalies") have been found in almost all the chemical elements (including the noble gases) of the refractory minerals of the carbonaceous meteorites. Because there is no experimental evidence that such effects can be achieved through chemical reactions, a nuclear origin for these isotopic anomalies has been postulated. This generally accepted interpretation of isotopic anomalies implies that interstellar minerals - often referred to as "pre-solar'' -, preserved in meteorites, were condensed in envelopes of supernovae that predated the formation of the solar system (Clayton et al. 1973; Wasserburg & Papanastassiou 1980; Ott 1993; Zinner 1995). Indeed, numerous astrophysical calculations have shown that these isotopic anomalies may be reconciled with the theoretical predictions of nucleosynthesis in stars. In some examples, remarkable agreements between meteorite data and nuclear physics calculations have been quantitatively achieved (see the extensive work of D. Clayton and his co-workers on this matter; for example Clayton et al. 1997, 2001).
In this paper, it will be shown that several anomalies share a common property which can be accounted for by a single formula describing the reaction rates of the different isotopomers of the same chemical element. Such a formula is based on a unique assumption: the rates involving reactions between indistinguishable isotopes are different from those involving distinguishable isotopes. This conclusion was reached (Robert et al. 1988; Robert & Baudon 1990; Robert & Camy-Peyret 2001) by studying the anomalous isotopic effect found during the synthesis of ozone (Mauersberger 1981; Mauersberger et al. 1999; Thiemens et al. 1999; Janssen et al. 2003; Mauersberger et al. 2003) and ascribed to a non-mass-dependent isotopic effect (Thiemens & Heidenreich III 1983).
Another theory accounting for the ozone effect has been proposed by Hathorn & Marcus (1999, 2000; see also Gao & Marcus 2001, 2002). In this theory, the non-mass-dependent isotopic fractionation effect is introduced as a free parameter which is supposed to be due to the fact that the density of quantum states of a vibrationally energetic molecule is greater for the symmetric than for the asymmetric molecules because there are fewer dynamical coupling terms in the symmetric than in the asymmetric molecules. Both theories reproduce quantitatively the individual reaction rates obtained by Mauersberger et al. (1999) and Janssen et al. (1999). However, the treatment by Robert & Camy-Peyret (2001) predicts positive and negative isotopic anomalies according to the energy at which the energetic molecule is stabilized while the Marcus et al. theory seems to preclude such negative effects. Therefore, beside future laboratory experiments, the meteorite data may help to distinguish which of these two proposals is correct.
In the present approach, the individual reaction rates for the different isotopomers are not calculated and consequently the isotopic fractionation factor is a free parameter. The proposed formalism allows the calculation of all the possible relations between the reactions rates normalized to a reference reaction. That is to say: if the isotopic fractionation factor of one isotopomer relative to an other isotopomer used as a reference is known, all the other isotopic fractionation factors involving all the other isotopomers are known. An example is given here after.
Let us consider a chemical element "I" having 3 stable isotopes, X, Y and Z
and 3 reactions among the 9 possible reactions involved in the reactions
I+IM:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
A numerical example is given in Table 1 for the 3 isotopes of oxygen. In Table 1, all individual rates are calculated and the total abundance of each isotope in all possible isotopomers are calculated. Let us take the example of the calculation of the relative abundance of 16O in the final molecules OOM with x16, x17 and x18 the relative natural abundance of 16O, 17O and 18O in the reactants and x'16, x'17 and x'18 the abundance of 16O, 17O and 18O in OOM (O in OOM stands for 16O, 17O or 18O).
Table 1:
A numerical example showing the mass-dependent
relations between the different reaction rates in the oxygen isotopic
system. In successive columns: (1) the isotopic reaction
iO+jOM
![]() OjOM; (2) the reduced mass of the
reactants for M=5; (3) the reduced mass ratio
OjOM; (2) the reduced mass of the
reactants for M=5; (3) the reduced mass ratio
![]() normalized to the reaction 16O+16OM for a=1;
(4) the product of the relative abundance with
normalized to the reaction 16O+16OM for a=1;
(4) the product of the relative abundance with
![]() ,
,
![]() and
and
![]() ;
(5) the
product of
;
(5) the
product of
![]() .
The 17O/16O ratio (
x'17/x'16) of the OOM molecule (noted
[17O/16O]
.
The 17O/16O ratio (
x'17/x'16) of the OOM molecule (noted
[17O/16O]
![]() is calculated from the values of the column
(5); that is:
is calculated from the values of the column
(5); that is:
![]()
![]() .
Similarly for
x'17 and x'18. This gives:
[17O/16O]
.
Similarly for
x'17 and x'18. This gives:
[17O/16O]
![]() and [18O/16O]
and [18O/16O]
![]() corresponding to
corresponding to
![]() O = ([
O = ([
![]() and similarly
and similarly
![]() .
The
slope in the diagram
.
The
slope in the diagram
![]() O versus
O versus
![]() O is equal to
0.513.
O is equal to
0.513.
![\begin{displaymath}x'_{16 }= \rm\left[^{16}O^{6}OM\right] + 1/2 \left[^{16}O^{17}OM\right] + 1/2
[^{16}O^{18}OM] .
\end{displaymath}](/articles/aa/full/2004/09/aa4131/img70.gif) |
(10) |
In isotopic ratios, the term in (10) appears as:
| (11) |
![\begin{displaymath}\rm with~~ \Delta \rm
\mu _{X-YM }^{\it a }= [\mu _{X-YM }/\mu _{16-16M} ]^{\it a }
\end{displaymath}](/articles/aa/full/2004/09/aa4131/img73.gif) |
(12) |
![\begin{displaymath}\delta ^{17}{\rm O}~ (\mbox{\mbox{\textperthousand}}) = {\{} [x'_{17}/ x'_{16}]_{ }/ [x_{17 }/
x_{16}]- 1 {\}} \times 1000
\end{displaymath}](/articles/aa/full/2004/09/aa4131/img75.gif) |
(13) |
In Table 1, the calculated ratio
![]() O/
O/
![]() O is
0.513, in close agreement with the experimental or theoretical ratio. Note
that the
O is
0.513, in close agreement with the experimental or theoretical ratio. Note
that the
![]() O/
O/
![]() O ratio is independent of the
value x16, x17 and x18 and almost independent of the value
of the mass M constituting the molecule OOM. Therefore this method can be
applied to all the chemical elements and will be used all along this paper
as a "proxy'' for the mass-dependent relations between rate constants
which only differ by the mass of their isotopically substituted molecules.
O ratio is independent of the
value x16, x17 and x18 and almost independent of the value
of the mass M constituting the molecule OOM. Therefore this method can be
applied to all the chemical elements and will be used all along this paper
as a "proxy'' for the mass-dependent relations between rate constants
which only differ by the mass of their isotopically substituted molecules.
In Sect. 2.2 discussing the non-mass-dependent isotopic fractionation,
the
![]() O/
O/
![]() O ratio is no longer independent of
the value x16, x17 and x18; therefore the notation of the
relative isotopic abundances were explicitly maintained in (11).
O ratio is no longer independent of
the value x16, x17 and x18; therefore the notation of the
relative isotopic abundances were explicitly maintained in (11).
The aim of this section is to propose a treatment that permits the calculation of a non-mass-dependent isotopic fractionation effect in a manner general to that described in Sect. 2.1. Similar to the treatment of the mass-dependent fractionation proposed in the previous Sect. 2.1, no specific chemical reaction is assigned for such a calculation.
This treatment is based on a single assumption: the rate constant for the
formation of molecules involving reactions between two indistinguishable
isotopes (such as X+XM) are not related in a mass-dependent manner to the
rate constants involving reactions between two distinguishable isotopes
(such as Y+XM). Such a difference does not appear in reactions such as (1)
to (3) but in 3-body reaction scheme where the formation of IIM occurs when
the stabilization of the energetic molecule IIM* involved two channels:
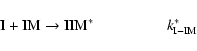 |
(14) |
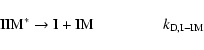 |
(15) |
| (16) |
| (17) |
![\begin{displaymath}\rm d[XXM] / d{\it t} = [X] [XM]
\{ k^*_{X-XM } {\it k}_N [N] / ({\it k}_{D,X-XM} + {\it k}_{N} [N] ) \}
\end{displaymath}](/articles/aa/full/2004/09/aa4131/img83.gif) |
(18) |
| (19) |
| (20) |
| (21) |
Let us consider the reactions yielding the formation of the 3 stable
molecules XXM, YXM and YYM; all the other possible rates involving all the
other isotopomers can be derived from these 3 reactions. The two isotopic
ratios
![]() and
and
![]() with the reaction X+XM used to
normalize the isotopic rate ratios are now calculated. To ease the
discussion of the numerical results, we will consider situations where the
"low pressure approximation" (i.e.
with the reaction X+XM used to
normalize the isotopic rate ratios are now calculated. To ease the
discussion of the numerical results, we will consider situations where the
"low pressure approximation" (i.e.
![]() )
applies;
that is:
)
applies;
that is:
![\begin{displaymath}R1= \rm\{ [Y] [XM] {\it k}^*_{Y-XM }{\it k}_{D,X-XM} \} /
\{[X] [XM] {\it k}^*_{X-XM }{\it k}_{D,Y-XM} \}.
\end{displaymath}](/articles/aa/full/2004/09/aa4131/img92.gif) |
(22) |
| (23) |
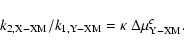 |
(24) |
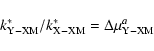 |
(25) |
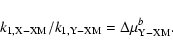 |
(26) |
The ratios R1 is:
| R1 | = | ||
| = | (27) |
![\begin{displaymath}R2 = [{\rm YYM}]/[{\rm XXM}] = yy \left\{\Delta \mu _{\rm Y-YM }^{a} \ \Delta \mu
_{\rm Y-YM}^{b } \right\} /\protect xx .
\end{displaymath}](/articles/aa/full/2004/09/aa4131/img99.gif) |
(28) |
Note that, contrary to the mass-dependent fractionation, the abundances of the isotopes (x, y and z) do not vanish in the final isotopic ratios of the molecule IIM stabilized via reaction (16). In this respect, the non-mass-dependent fractionation can be defined as "abundance dependent'', because the mass-dependent effects are second order contributions to the overall fractionation.
The parameter "a" stands for the classical isotopic fractionation factor under equilibrium between the reactants and the energetic molecule. The parameter "b" stands for the mass-dependent fractionation occurring during the dissociation of the energetic molecule. The parameter "c" has no counterpart in the classical theory of isotopic fractionation. The study of ozone has shown that these parameters were constant through the various conditions of the ozone synthesis. In the minerals of meteorites, these conditions are unknown and these parameters will be considered as free.
When the low pressure approximation does not apply, the isotopic variations
with pressure can be reproduced by such a formalism since ![]() [N]/
[N]/![]() is proportional to P/P0 with P the pressure at which the
energetic molecule is stabilized (see the calculation of P/P0 in Robert
and Camy-Peyret). Defining
is proportional to P/P0 with P the pressure at which the
energetic molecule is stabilized (see the calculation of P/P0 in Robert
and Camy-Peyret). Defining
| (29) |
| (30) |
The aim of this section is to compare the theoretical predictions proposed in Sect. 2.2. with the results obtained for different chemical elements. The isotopic anomalies observed in meteorites are used for that purpose. However, it should be noted that in meteorites, isotopic anomalies are mostly found in high temperature minerals (condensed from a gas at temperature between 1500 and 2200 K), suggesting that the conditions (temperature and pressure) under which these isotopic anomalies were established in meteorites are quite different from those prevailing during the ozone synthesis.
The numerical results reported in this section were obtained for different
values of the parameter ![]() and different values of the
parameters "a", "b" and "c" which dictate the mass dependence between the
constants. According to the interpretation of (20),
and different values of the
parameters "a", "b" and "c" which dictate the mass dependence between the
constants. According to the interpretation of (20), ![]() can vary
between 0 and
can vary
between 0 and ![]() 1 (see Robert & Camy-Peyret 2001). Thus, this type
of non-mass-dependent isotopic fractionation can yield both positive (for
1 (see Robert & Camy-Peyret 2001). Thus, this type
of non-mass-dependent isotopic fractionation can yield both positive (for
![]() )
and negative (for
)
and negative (for
![]() )
)
![]() values.
values.
The parameter "a" dictates the isotopic fractionation between atoms and
molecules. In ozone, it has been experimentally shown (Mauersberger 1999)
that this fractionation is governed by the isotopic equilibrium between
atoms and molecules, the number of collisions yielding an isotopic exchange
between O and O2 greatly exceeding those forming O3: O atoms have
a
![]() and a
and a
![]() ,
relative to
O2. In meteoritic minerals, such a pseudo isotopic equilibrium between
atoms and molecules is not necessarily the case because the source of the
atoms may be decoupled from that of the molecules (as for example when a
source of atoms - stellar winds in astronomical situations (?) - interfere
with a cold molecular medium). This remark is important for heavy elements
(>30 amu) which are known to exhibit almost no mass-dependent isotopic
fractionation at high temperature (i.e.
,
relative to
O2. In meteoritic minerals, such a pseudo isotopic equilibrium between
atoms and molecules is not necessarily the case because the source of the
atoms may be decoupled from that of the molecules (as for example when a
source of atoms - stellar winds in astronomical situations (?) - interfere
with a cold molecular medium). This remark is important for heavy elements
(>30 amu) which are known to exhibit almost no mass-dependent isotopic
fractionation at high temperature (i.e.
![]() or
or
![]() ). Thus, in astronomical conditions, the parameter "a" may a priori
greatly exceed that expected from equilibrium or kinetic reactions between
atoms and molecules.
). Thus, in astronomical conditions, the parameter "a" may a priori
greatly exceed that expected from equilibrium or kinetic reactions between
atoms and molecules.
Two implicit assumptions are made in the numerical applications (these assumptions are classical in geochemistry). (1) Atoms and molecules are considered as infinite reservoirs. In other terms, the isotopic compositions of the reactants are constant in time. (2) The possible mixing in the meteoritic matter of several minerals carrying distinct isotopic anomalies is ignored. Nevertheless this complex situation does occur in the meteoritic matter, as illustrated by the grain size of the carriers of isotopic anomalies whose dimensions - in some examples - do not exceed 100 nanometers. In such situations an isotopic composition cannot be assigned (and measured) for each individual grain.
Table 2:
A numerical example showing the non-mass-dependent
relations between the different reaction rates in the oxygen isotopic
system. In successive columns: (1) the isotopic reaction
iO+jOM
![]() OjOM; (2) the reduced mass
ratio
OjOM; (2) the reduced mass
ratio
![]() /
/
![]() for a=0.1 and M=5; (3)
for a=0.1 and M=5; (3)
![]() for b=
0.2; (4)
for b=
0.2; (4)
![]() for c= 0.1; (5) the
reaction rate ratio R. Two situations are distinguished: (1) for
iO+ iOM (
for c= 0.1; (5) the
reaction rate ratio R. Two situations are distinguished: (1) for
iO+ iOM (![]() ),
),
![]() and for (2) jO+ iOM (
and for (2) jO+ iOM (![]() ),
),
![]() 1/2
[
1/2
[
![]() ]; calculations
are performed for
]; calculations
are performed for
![]() (6) The product of the
relative abundance with
(6) The product of the
relative abundance with
![]() ,
,
![]() and
and
![]() (7) the product of
(7) the product of
![]() .
The 17O/16O ratio of the OOM molecule (noted
[17O/16O]
.
The 17O/16O ratio of the OOM molecule (noted
[17O/16O]
![]() is calculated from the values of the column
[7]; that is for the abundance of 16O: {1/2 [
is calculated from the values of the column
[7]; that is for the abundance of 16O: {1/2 [
![]() } and similarly for 17O and 18O. The
} and similarly for 17O and 18O. The
![]() O (
O (
![]() )
= ([17O/16O]
)
= ([17O/16O]
![]() /[0.0004/0.9976])- 1)
/[0.0004/0.9976])- 1)
![]() 1000; similarly for
1000; similarly for
![]() O (
O (
![]() ). That is:
). That is:
![]() and
and
![]() with
with
![]() O/
O/
![]() .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{figure1.eps}\end{figure}](/articles/aa/full/2004/09/aa4131/Timg120.gif) |
Figure 1:
Five examples of isotopic anomalies
measured in meteorites are compared with the present calculations (black
dots for calculations and open symbols for data). The calculated patterns
were adjusted to the measured values through the parameters |
| Open with DEXTER | |
In the following numerical calculations, the approximations made in Eqs. (27) and (28) will be used. For clarity, an example of a complete calculation is reported in Table 2. From this example it is possible to derived all the other numerical applications for the other isotopic systems reported in the Figs. 1 to 4.
The results are reported in the 3 usual units used in Cosmochemistry: in
![]() units, in
units, in
![]() units (
units (
![]() )
and in
)
and in
![]() units using the normalization to
two isotopes. In this last unit, because of analytical limitations, the
absolute
units using the normalization to
two isotopes. In this last unit, because of analytical limitations, the
absolute
![]() values cannot be determined and another isotope is
used as a second reference. In this unit, the isotopic compositions of the
two reference isotopic ratios are assumed to be related in a mass-dependent
manner and the isotopic compositions of the other masses are corrected by
this mass-dependent term. In this unit, the mass-dependent fractionation
yields
values cannot be determined and another isotope is
used as a second reference. In this unit, the isotopic compositions of the
two reference isotopic ratios are assumed to be related in a mass-dependent
manner and the isotopic compositions of the other masses are corrected by
this mass-dependent term. In this unit, the mass-dependent fractionation
yields
![]() at all masses.
at all masses.
In these 3 units, the different diagrams reported in the Figs. 1 to 4 have the following properties.
Three different types of examples are distinguished in the Figs. 1 to 3. In Fig. 1, some of the classic examples of the Cosmochemical literature are reported and compared with the present numerical simulations. In Fig. 2, an example of the pressure effect is given for the silicon isotopes and compared with the meteorite data. In Fig. 3, two examples of meteorite data that cannot be reproduced by the present numerical simulation are shown. This may illustrate the limitations of our various assumptions (and especially the chosen mass-dependent relations) or the fact that these anomalies are purely nuclear or - of course - that the present theory is incorrect...
As far as the adjustments of the parameters of the calculation that fit the
meteorite data are concerned two remarks should be made: (1) In most
examples the parameter "a" plays the same role as the parameter "b"; hence
"a" can be generally assigned to be equal to 0. Thus, the calculated
patterns reported in the figures depend only on 3 free parameters: ![]() ,
b and c (2); Often - not always - the patterns can be translated to much
higher
,
b and c (2); Often - not always - the patterns can be translated to much
higher ![]() units without changing the general shape of the patterns.
This translation is obtained by multiplying the parameters by a constant
factor. This indicates that the dilution of the measured anomalous isotopic
composition by a "normal" (i.e. not fractionated or mass fractionated)
composition does not change the predictions of the theory.
units without changing the general shape of the patterns.
This translation is obtained by multiplying the parameters by a constant
factor. This indicates that the dilution of the measured anomalous isotopic
composition by a "normal" (i.e. not fractionated or mass fractionated)
composition does not change the predictions of the theory.
In this section we give a few examples of possible reactions yielding non-mass-dependent isotopic effects and which could be studied in the laboratory. These chemical systems are difficult to predict for three reasons: (1) the formula of the energetic molecules that can be formed during a given reaction are poorly known; (2) the determination of their lifetime is a difficult theoretical task and (3) this lifetime should be long enough in order for the energetic molecule to be involved in a second reaction, as for example its stabilization by a third body. The stabilization of the energetic molecule is certainly not the only way to retrieve the reactants from a chemical system and thus to give rise to a non-mass-dependent isotopic effect. As long as there is a competition between the isotopic exchange and the removal rates i.e. as long as two channels are open (see Appendix), the products of the reaction should be isotopically fractionated in a non-mass-dependent manner.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure2.eps}\end{figure}](/articles/aa/full/2004/09/aa4131/Timg125.gif) |
Figure 2:
The silicon isotopic variations (expressed in
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{newfigure3.eps}\end{figure}](/articles/aa/full/2004/09/aa4131/Timg126.gif) |
Figure 3:
Two examples of isotopic anomalies measured in
meteorites which cannot be reconcile with the present theory (isotope ratios
expressed in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figure4.eps}\end{figure}](/articles/aa/full/2004/09/aa4131/Timg127.gif) |
Figure 4:
Neodymium isotopic anomalies in the refractory
inclusion EK 1-4-1 and in SiC (Nd, normalization at mass 142; data from
McCulloch & Wasserburg 1978a and from Richter et al. 1992). The
calculation is performed by adjusting the parameter |
| Open with DEXTER | |
In a medium where high density reactive species or ions are present, the formation of energetic molecules able to react or to condense on a solid phase is markedly enhanced. Since these energetic molecules rarely appear spontaneously in a thermal gas, photochemistry or irradiation by hot atoms should promote this type of isotopic fractionation.
As far as the oxygen isotopic composition is concerned, the reactions
between oxides and metastable oxygen species may yield this type of isotopic
selection:
| (31) |
In other elements, reactions between several oxides of the same element may
also satisfy the requirement of the 3-body reaction scheme. Titanium is
taken as an example:
| (32) |
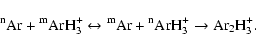 |
(33) |
In the case of the interactions between a solid and a (rare) gas, another
process should be mentioned. The factors that control the rate of the
various adsorption and desorption processes may have interesting
similarities with the non-mass-dependent reaction scheme proposed here. The
overall process for a precursor-mediated adsoption can be described as:
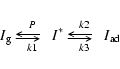 |
(34) |
There are numerous examples demonstrating that nuclear effects are indeed present in meteoritic minerals and it is not the aim of this paper to claim that all isotopic anomalies result from the non-mass-dependent isotopic fractionation effect reported here. However, as often noted in the literature, interpreting all anomalies as the result of nuclear effects during supernova explosions is a difficult task. In many cases such as C, N, Si, etc., and in the framework of the nuclear interpretation, the distribution of the isotopic compositions observed in meteoritic minerals must result from the contribution of grains condensed in the envelopes of different stars at different periods of the Galactic chemical evolution. For example, in the case of silicon isotopes, it seems almost impossible that the same star can produce the whole range of isotopic compositions defining the 1.3 slope correlation reported in Fig. 2. As illustrated by the calculation reported in Fig. 2, such an issue is overcome by the present treatment.
In many examples, positive and negative isotopic anomalies are observed for the same element but in different minerals. If these anomalies are nuclear, these observations have profound consequences for the origin of the chemical composition of our own solar system: isotopic anomalies cannot be viewed as a simple addition of freshly nucleosynthesized isotopes to the average, isotopically normal, solar system matter because such an addition would yield systematic isotopic enhancements. On the contrary, it must be supposed that the average solar system composition results from a thorough mixture of isotopic anomalies.
The present theory offers an alternative interpretation to this difficulty because the 3-body reaction scheme can, in principle yields positive or negative anomalies.
The mass balance calculation between the two channels can be performed as
follows:
| (35) |
| (36) |
| (37) |
For this element a slight positive isotopic anomaly was observed in the
refractory inclusion EK 1-4-1 of the Allende meteorite and a large negative
anomaly in SiC. Let us assign the negative anomaly to the dissociation of
the energetic molecule and the positive one to its stabilization. To
reinforce the value of this calculation, the numerical results reported in
Fig. 4 depend on only one parameter (![]() .
The negative
.
The negative
![]() Nd at mass m=143 was chosen to adjust
Nd at mass m=143 was chosen to adjust
![]() (
(
![]() ). All the mass-dependent parameters were ignored
i.e. a=b=c=0. In other terms, the only isotope adjusted in the calculation
is at mass 143 while all the others (at mass 144, 145, 146,148 and 150 for
the negative
). All the mass-dependent parameters were ignored
i.e. a=b=c=0. In other terms, the only isotope adjusted in the calculation
is at mass 143 while all the others (at mass 144, 145, 146,148 and 150 for
the negative ![]() pattern and at mass 143, 144, 145, 146, 148 and
150 for the positive
pattern and at mass 143, 144, 145, 146, 148 and
150 for the positive ![]() pattern) are calculated rigorously. As
reported in Fig. 4, the calculation shows close similarity to
observations.
pattern) are calculated rigorously. As
reported in Fig. 4, the calculation shows close similarity to
observations.
The calculated positive pattern is nevertheless enhanced in
![]() Nd by a factor of 20 relative to the observed pattern; for example
the calculated
Nd by a factor of 20 relative to the observed pattern; for example
the calculated
![]() Nd is
Nd is
![]() as compared to the observed value
of
as compared to the observed value
of
![]() .
This can be interpreted as a dilution with isotopically normal Nd
since - as already mentioned - such a dilution process does not change the
relative position of the isotopic compositions in the anomalous pattern.
.
This can be interpreted as a dilution with isotopically normal Nd
since - as already mentioned - such a dilution process does not change the
relative position of the isotopic compositions in the anomalous pattern.
It is remarkable that this calculation reproduces not only the two patterns
at all masses, but also that the large negative isotopic anomalies (in the
range of
![]() )
correspond to moderate positive one (in the range of
)
correspond to moderate positive one (in the range of
![]() ).
This does not imply that the two types of grains carrying the anomalies are
co-genetic but that they can result from a similar isotopic fractionation
process.
).
This does not imply that the two types of grains carrying the anomalies are
co-genetic but that they can result from a similar isotopic fractionation
process.
Compared with the nuclear interpretation, the present approach faces two types of difficulties. First, one can calculate numerous isotopic anomalies with the present treatment that are not observed in meteorites. Second, the chemical reactions at the origin of the calculated effects are not identified. The two difficulties are linked since the parameters of the isotopic fractionation correspond probably to a given chemical reaction (as shown for ozone). The situation is probably even more complicated because nuclear effects and non-mass-dependent effects could be intimately associated in the meteoritic minerals.
The concept of presolar grains (i.e. grains carrying isotopic anomalies) is not questioned by the present theory since it is not possible to decide if the chemical non-mass-dependent process took place (or not) during the formation of our own solar system, especially during the T-Tauri phase of the early Sun.
It is presently proposed that in chemical reactions, when isotopes are
indistinguishable, the rate constant ![]() for the dissociation of an energetic
molecule should be written as:
for the dissociation of an energetic
molecule should be written as:
| (38) |
| (39) |
The isotopic effect proposed by Robert & Camy-Peyret (2001) can be
illustrated by comparing - in a 3-body reaction scheme - reactions involving
distinguishable and indistinguishable isotopes. Two situations can be
envisaged:
Situation 1
![\begin{displaymath}\includegraphics[width=8.5cm]{aa4131f1.eps}\end{displaymath}](/articles/aa/full/2004/09/aa4131/img142.gif)
![\begin{displaymath}\includegraphics[width=8.5cm]{aa4131f2.eps}\end{displaymath}](/articles/aa/full/2004/09/aa4131/img143.gif)
Since in quantum mechanics - and contrary to classical mechanics - the two
values of the impact parameter may have different probabilities, one has:
1/2
![]() .
.
Such an inequality is at the origin of the non-mass-dependent isotopic effect.
However, as noted by R. Marcus (pers. com.) this interpretation implies that the lifetime of the energetic molecule XXM* is related to the value of the impact parameter from which the molecule has been formed. In other terms, the energetic molecule should not "forget" the conditions of its formation. This issue remains uncertain since, after its formation by the collision X-XM, the energetic molecule rotates and redistributes its internal energy in a chaotic manner. No quantum calculations of such an effect have yet been performed.
Acknowledgements
I would like to thank Samuel Epstein who passed away just two years ago; he let me work on the idea developed in this paper during my post-doctoral fellowship at Caltech in 1984 (I was supposed to work on cherts!) and ever since he encouraged me to publish it. Now it's done. Dr. R. Marcus reviewed this paper and I would also like to thank him for making me understand the conditions and limits of my interpretation. Our discussions, along with Dr. Micallef, have greatly improved this text.