We have used the angular velocity as a control parameter instead of the angular momentum for commodity but also because it is the most natural variable to characterize a rotating system. Indeed, the conservation of angular momentum should not be taken in a strict sense because it can always be satisfied by ejecting a small amount of mass far away with weak influence on the other constraints. For similar remarks concerning the role of angular momentum in the context of vortex dynamics, see Brands et al. (1999).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

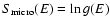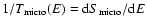Of course, in a strict sense, the microcanonical caloric curve must be single valued everywhere because $S_{\rm micro}(E)=\ln g(E)$ and $1/T_{\rm micro}(E)={\rm d}S_{\rm micro}/{\rm d}E$ (Gross 2001, 2003). However, the caloric curves that we represent are richer because they contain saddle points SP (unstable), local maxima LEM (metastable) and global maxima GEM (stable) of entropy. 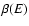Had we represented only global entropy maxima, the curves S(E) and $\beta(E)$ would be single-valued. 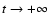They would describe the true statistical equilibrium states reached for $t\rightarrow +\infty$ . However, metastable states are of considerable importance in astrophysics because they correspond to the observed structures (e.g., globular clusters) for the timescales contemplated (as is well known, stellar systems are not in true statistical equilibrium states). Therefore, the physical caloric curves must take these metastable states into account and this gives rise to what we have nicknamed "dinosaur's necks''. We recall that these metastable states appear only for sufficiently small cut-offs. For large cut-offs (see Fig. 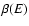1), there is only one global entropy maximum for each energy and the $\beta(E)$ curve is univalued. This is the situation considered by Votyakov et al. (2002) (compare their Fig. 7 to our Fig. 3).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... equilibrium

A Fermi-Dirac distribution in configuration space also arises in the statistical mechanics of two-dimensional vortices (see Chavanis 2002a for a review on the analogy between stellar systems and 2D vortices). In that respect, it may be relevant to mention the work of Chen & Cross (1996) who found "double-vortex'' equilibrium solutions in a circular domain when the conservation of angular momentum is accounted for. This can be viewed as the 2D hydrodynamical version of the "double-star'' structure found by Votyakov et al. (2002). Note that the presence of a confining box is crucial to maintain the double-vortex solution. Similarly, for self-gravitating systems at non-zero temperature, an artificial box is needed to maintain the double-star structure.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... gas

In fact, Votyakov et al. (2002) prevent overlapping of particles in physical space, as in a lattice gas model. This is a simple way to limit the local density 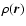$\rho({\vec r})$ of the self-gravitating gas. Hence, their model is expected to represent stars at densities up to the ignition of their hydrogen burning, when further gravitational collapse is halted for a while (Gross 2003). In this context, it may be relevant to consider a large small-scale cut-off, as they do. Note that their model does not correspond to the Lynden-Bell (1967) statistics, which is a Fermi-Dirac distribution in phase space appropriate to collisionless stellar systems (e.g., Chavanis 2002d).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.