D. Pierini1 - C. C. Popescu2,3 - R. J. Tuffs2 - H. J. Völk2
1 - Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstr., 85748 Garching, Germany
2 - Max-Planck-Institut für Kernphysik,
Saupfercheckweg 1, 69117 Heidelberg, Germany
3 - Research Associate, The Astronomical Institute of the Romanian
Academy, Str. Cutitul de Argint 5, Bucharest, Romania
Received 19 March 2003 / Accepted 29 July 2003
Abstract
We present the correlation between the far-infrared (FIR) and radio
emissions from a composite sample of 72 nearby normal galaxies observed with
the ISOPHOT instrument on board the Infrared Space Observatory.
The galaxies in the sample have measurements at three FIR wavelengths
(60, 100 and 170 ![]() m), which allowed a direct determination of
the warm and cold FIR emission components.
This is the first time that the correlation has been established
for the total FIR luminosity, of which most is carried by the cold dust
component predominantly emitting longwards of the spectral coverage of IRAS.
The slope of this correlation is slightly non-linear (
m), which allowed a direct determination of
the warm and cold FIR emission components.
This is the first time that the correlation has been established
for the total FIR luminosity, of which most is carried by the cold dust
component predominantly emitting longwards of the spectral coverage of IRAS.
The slope of this correlation is slightly non-linear (
![]() ).
Separate correlations between the warm and cold FIR emission components
and the radio emission have also been derived.
The slope of the warm FIR/radio correlation was found to be linear
(
).
Separate correlations between the warm and cold FIR emission components
and the radio emission have also been derived.
The slope of the warm FIR/radio correlation was found to be linear
(
![]() ).
For the cold FIR/radio correlation we found a slightly non-linear
(
).
For the cold FIR/radio correlation we found a slightly non-linear
(
![]() )
slope.
We qualitatively interpret the correlations in terms of star formation rate
and find that both the FIR and radio emissions may be consistent with
a non-linear dependence on star formation rate for galaxies not undergoing
starburst activity.
)
slope.
We qualitatively interpret the correlations in terms of star formation rate
and find that both the FIR and radio emissions may be consistent with
a non-linear dependence on star formation rate for galaxies not undergoing
starburst activity.
Key words: galaxies: spiral - galaxies: stellar content - galaxies: ISM - infrared: galaxies - radio continuum: galaxies
One of the most surprising discoveries of the IRAS all-sky survey was the very tight and universal correlation between the spatially integrated far-infrared (FIR) and radio continuum emissions of late-type galaxies (de Jong et al. 1985; Helou et al. 1985; Wunderlich et al. 1987). The standard interpretation of the so-called FIR/radio correlation is in terms of massive star formation activity (see Condon 1992; Völk & Xu 1994 for reviews). This picture assumes that the FIR emission is due to dust heated by the massive stars which are also responsible for the radio emission: the ionising radiation from the massive stars powers the thermal radio emission, and the remnants of supernova explosions which occur at the end of their lives presumably accelerate the cosmic ray electrons. The link between the radio synchrotron and dust emissions was quantified by the calorimeter theory of Völk (1989) (see also Lisenfeld et al. 1996). Specific aspects of the FIR/radio correlation have been addressed by many authors (e.g. Gavazzi et al. 1986; Cox et al. 1988; Devereux & Eales 1989; Chi & Wolfendale 1990; Condon et al. 1991; Price & Duric 1992; Xu et al. 1994a; Xu et al. 1994b; Niklas et al. 1995; Lisenfeld et al. 1996; Bressan et al. 2002; Bell 2003; Groves et al. 2003).
All these studies of the FIR/radio correlation were based on
IRAS measurements and FIR luminosities obtained by
using the IRAS flux densities at 60 and 100 ![]() m.
However the FIR spectral energy distribution (SED) of
normal
m.
However the FIR spectral energy distribution (SED) of
normal![]() galaxies
typically peaks longwards of 100
galaxies
typically peaks longwards of 100 ![]() m, beyond the spectral grasp
of IRAS, as predicted from submillimeter (submm) observations by
Chini et al. (1986).
With the advent of the Infrared Space Observatory (ISO)
(Kessler et al. 1996), in particular of the ISOPHOT instrument
(Lemke et al. 1996) on board ISO, it became routinely possible to measure
the peak of the FIR emission, also for fainter objects not detected by IRAS.
It was found that, especially for quiescent galaxies, most of
the FIR luminosity is carried by a cold dust component (Popescu et al. 2002)
whose luminosity is not well predicted by the IRAS measurements.
In fact the luminosity correction factors
m, beyond the spectral grasp
of IRAS, as predicted from submillimeter (submm) observations by
Chini et al. (1986).
With the advent of the Infrared Space Observatory (ISO)
(Kessler et al. 1996), in particular of the ISOPHOT instrument
(Lemke et al. 1996) on board ISO, it became routinely possible to measure
the peak of the FIR emission, also for fainter objects not detected by IRAS.
It was found that, especially for quiescent galaxies, most of
the FIR luminosity is carried by a cold dust component (Popescu et al. 2002)
whose luminosity is not well predicted by the IRAS measurements.
In fact the luminosity correction factors![]() for cold dust do not correlate
with Hubble type and exhibit a huge scatter, with mean values ranging from
1 to 3 (Popescu & Tuffs 2002).
In view of this, there is a clear need to redefine the FIR/radio correlation
in terms of the total FIR-submm luminosity, as derived from
ISO measurements.
for cold dust do not correlate
with Hubble type and exhibit a huge scatter, with mean values ranging from
1 to 3 (Popescu & Tuffs 2002).
In view of this, there is a clear need to redefine the FIR/radio correlation
in terms of the total FIR-submm luminosity, as derived from
ISO measurements.
Another result to emerge from ISO is the confirmation that
the FIR SEDs of normal galaxies require a warm and a cold dust
emission component to be fitted (for a review see Tuffs & Popescu 2003).
Although the concept of warm and cold emission components is as old as IRAS
(de Jong et al. 1984), it only became possible to directly measure
and separate these components with ISO, due to its spectral grasp
and multi filter coverage of the FIR regime.
The warm component can be identified with locally heated dust
in HII regions![]() and the cold component with dust distributed in the general
diffuse interstellar medium and heated by a combination of
non-ionising ultraviolet (UV) and optical/near-IR photons.
This interpretation is consistent with what has been seen
in the ISOPHOT maps of nearby galaxies (e.g. Haas et al 1998;
Hippelein et al. 2003).
It is also consistent with models of the UV/optical/FIR/submm SEDs
in normal galaxies, which self-consistently calculate
a continuous distribution of dust temperatures based on
radiative-transfer calculations (Silva et al. 1998; Popescu et al. 2000;
Misiriotis et al. 2001).
Thus ISO measurements give us the first direct opportunity of defining
the FIR/radio correlation separately for the warm and cold dust components.
In the past this could only be indirectly attempted by constraining
the warm dust component to be proportional to the H
and the cold component with dust distributed in the general
diffuse interstellar medium and heated by a combination of
non-ionising ultraviolet (UV) and optical/near-IR photons.
This interpretation is consistent with what has been seen
in the ISOPHOT maps of nearby galaxies (e.g. Haas et al 1998;
Hippelein et al. 2003).
It is also consistent with models of the UV/optical/FIR/submm SEDs
in normal galaxies, which self-consistently calculate
a continuous distribution of dust temperatures based on
radiative-transfer calculations (Silva et al. 1998; Popescu et al. 2000;
Misiriotis et al. 2001).
Thus ISO measurements give us the first direct opportunity of defining
the FIR/radio correlation separately for the warm and cold dust components.
In the past this could only be indirectly attempted by constraining
the warm dust component to be proportional to the H![]() emission,
as done by Xu et al. (1994b).
These authors established separate relations for the warm FIR/radio
correlation and the cold FIR/radio correlation.
However, the cold FIR luminosity derived in this study was based on
IRAS data, and misses the bulk of the true cold dust luminosity.
Other authors have used different operational recipes with different
physical interpretations to derive warm and cold FIR emission components
from IRAS data for comparison with radio data (e.g. Beck & Golla 1988;
Fitt et al. 1988; Wunderlich & Klein 1991; Condon et al. 1991;
Hoernes et al. 1998), but again these studies missed the bulk of
the cold dust emission.
emission,
as done by Xu et al. (1994b).
These authors established separate relations for the warm FIR/radio
correlation and the cold FIR/radio correlation.
However, the cold FIR luminosity derived in this study was based on
IRAS data, and misses the bulk of the true cold dust luminosity.
Other authors have used different operational recipes with different
physical interpretations to derive warm and cold FIR emission components
from IRAS data for comparison with radio data (e.g. Beck & Golla 1988;
Fitt et al. 1988; Wunderlich & Klein 1991; Condon et al. 1991;
Hoernes et al. 1998), but again these studies missed the bulk of
the cold dust emission.
In this paper we redefine the FIR/radio correlation using for the first time the total FIR luminosity (as measured with ISO) for a statistical sample. Plots of the FIR/radio correlation using the new ISO measurements were also given in Popescu et al. (2002), but only for a very small sample, and therefore no attempt was made to quantify the linearity of the correlation there. The goal of this paper is to provide a statistical analysis of the correlation and also to derive the slope of the correlation separately for the warm and cold dust components. Finally the new results are discussed in the context of predictions of theoretical models on photon heating of dust in normal star-forming galaxies.
The paper is organised as follows. In Sect. 2 we describe the sample selection and the analysis of the radio data. In Sect. 3 we present the results for the total FIR/radio correlation, as well as for the warm and cold FIR/radio correlations. Each of these correlations is qualitatively analysed in terms of its dependence on the star formation rate in Sect. 4. In Sect. 5 we discuss scenarios which can simultaneously account for both the warm and cold FIR/radio correlations. A summary is given in Sect. 6.
The sample used in this study is a combination of a very deep,
optically selected sample of normal, relatively quiescent galaxies
together with a shallow, FIR selected sample of relatively bright galaxies.
This provides us with a high dynamic range in FIR luminosities as well as
good statistics.
For this purpose we used the ISOPHOT Virgo Cluster Deep Survey
(Tuffs et al. 2002,b), which is the deepest survey (both in luminosity
and surface brightness terms) of normal galaxies performed by ISOPHOT,
and the ISOPHOT 170 ![]() m Serendipity Survey (Stickel et al. 2000).
All galaxies in the combined sample have had their integrated flux densities
measured by ISOPHOT at 170
m Serendipity Survey (Stickel et al. 2000).
All galaxies in the combined sample have had their integrated flux densities
measured by ISOPHOT at 170 ![]() m (the Virgo galaxies also
in the ISOPHOT bands centered at 60 and 100
m (the Virgo galaxies also
in the ISOPHOT bands centered at 60 and 100 ![]() m).
Most galaxies from the Virgo sample are freshly falling in from the field
(Tully & Shaya 1984; Tuffs et al. 2002,b) and therefore
we consider it legitimate to combine it with the ISOPHOT 170
m).
Most galaxies from the Virgo sample are freshly falling in from the field
(Tully & Shaya 1984; Tuffs et al. 2002,b) and therefore
we consider it legitimate to combine it with the ISOPHOT 170 ![]() m
Serendipity Survey sample.
Furthermore there is no evidence for an effect of the cluster environment
on the FIR properties of the galaxies from the ISOPHOT Virgo Cluster
Deep Sample (Popescu et al. 2002; Popescu & Tuffs 2002).
This is to be expected since the bulk of the FIR emission arises primarily
from the inner regions of the galactic disks.
The radio emission may be more prone to alterations due to
environmental effects, as we will discuss in Sect. 3.
However we will show there that, in the case of our sample,
these effects are only of second order.
Thus, in this paper we regard the main distinction between Virgo
and Serendipity Survey galaxies to be the quiescent nature of the former,
rather than their association with the cluster environment.
So, put together, the combined sample will provide us with larger statistics
and a good dynamic range in star formation activity.
m
Serendipity Survey sample.
Furthermore there is no evidence for an effect of the cluster environment
on the FIR properties of the galaxies from the ISOPHOT Virgo Cluster
Deep Sample (Popescu et al. 2002; Popescu & Tuffs 2002).
This is to be expected since the bulk of the FIR emission arises primarily
from the inner regions of the galactic disks.
The radio emission may be more prone to alterations due to
environmental effects, as we will discuss in Sect. 3.
However we will show there that, in the case of our sample,
these effects are only of second order.
Thus, in this paper we regard the main distinction between Virgo
and Serendipity Survey galaxies to be the quiescent nature of the former,
rather than their association with the cluster environment.
So, put together, the combined sample will provide us with larger statistics
and a good dynamic range in star formation activity.
In total 72 galaxies were selected, as described below. Of these, 20 galaxies show some evidence for LINER/Seyfert activity or are pair/multiple/merger systems.
The ISOPHOT Virgo Cluster Deep Sample consists of 63 galaxies later than S0
and brighter than
![]() ,
selected from the Virgo Cluster
Catalogue (VCC) of Binggeli et al. (1985).
Tuffs et al. (2002,b) have presented deep diffraction-limited
FIR strip maps of this sample, obtained with ISOPHOT
at the central wavelengths 60, 100 and 170
,
selected from the Virgo Cluster
Catalogue (VCC) of Binggeli et al. (1985).
Tuffs et al. (2002,b) have presented deep diffraction-limited
FIR strip maps of this sample, obtained with ISOPHOT
at the central wavelengths 60, 100 and 170 ![]() m
m![]() .
Details of observations, data reduction, estimate of
the calibration uncertainty and procedure of extraction of photometry
are given in Tuffs et al. (2002,b).
As discussed by these authors, the 63 galaxies represent a sample
of nearby normal (i.e. non-AGN dominated and non-starburst)
late-type galaxies.
Nevertheless a few objects have also some mild LINER/Seyfert activity.
.
Details of observations, data reduction, estimate of
the calibration uncertainty and procedure of extraction of photometry
are given in Tuffs et al. (2002,b).
As discussed by these authors, the 63 galaxies represent a sample
of nearby normal (i.e. non-AGN dominated and non-starburst)
late-type galaxies.
Nevertheless a few objects have also some mild LINER/Seyfert activity.
Out of this sample, 38 galaxies (i.e. 63.5 per cent of the total)
were detected at all three wavelengths.
Most of them were discovered to contain a cold dust emission component
which could not have been recognised by IRAS, irrespective of
the morphological classification of individual objects
(Popescu et al. 2002).
The ISOPHOT FIR SEDs of these galaxies were fitted with a combination
of two modified blackbody functions, physically identified with
the emissions from a localised warm dust component, with a fixed temperature
of 47 K, and a diffuse cold dust component (see Popescu et al.).
The cold dust temperatures were found to span a broad range,
with a median of 18 K.
The physical justification for fixing the temperature of the warm component
is based on the modelling work of Popescu et al. (2000)
and Misiriotis et al. (2001).
The latter papers showed that ![]() 20 per cent
of the integrated FIR emission at 60
20 per cent
of the integrated FIR emission at 60 ![]() m comes from
stochastically heated grains in the diffuse interstellar medium (ISM),
m comes from
stochastically heated grains in the diffuse interstellar medium (ISM),
![]() 20 per cent from optically heated grains in the diffuse ISM,
and
20 per cent from optically heated grains in the diffuse ISM,
and ![]() 60 per cent from HII regions.
So it is a good physical approximation to consider that most of the emission
at
60 per cent from HII regions.
So it is a good physical approximation to consider that most of the emission
at ![]() m comes from grains within the HII regions (which do not emit
stochastically).
Although there is a variation in grain temperature between HII regions
in any given galaxy (Peeters et al. 2002) (due to changes in size, geometry
and exciting stars), these are quite moderate (in comparison to
the systematic difference in temperature between grains in HII regions
and grains in the diffuse ISM).
Thus, if we average over the ensemble of HII regions in each galaxy
we would expect the ensemble of HII regions to have virtually identical SEDs
from one galaxy to the next.
m comes from grains within the HII regions (which do not emit
stochastically).
Although there is a variation in grain temperature between HII regions
in any given galaxy (Peeters et al. 2002) (due to changes in size, geometry
and exciting stars), these are quite moderate (in comparison to
the systematic difference in temperature between grains in HII regions
and grains in the diffuse ISM).
Thus, if we average over the ensemble of HII regions in each galaxy
we would expect the ensemble of HII regions to have virtually identical SEDs
from one galaxy to the next.
Fourteen of the 38 galaxies with both warm and cold dust emission components have also been detected in the radio continuum at 1.4 GHz, thanks to the recent NRAO/VLA Sky Survey (NVSS) (Condon et al. 1998). For these objects we performed aperture photometry to extract integrated flux densities from the NVSS maps (see Appendix A, only available in the on-line edition of the journal). The 14 VCC galaxies with FIR and radio counterparts are considered in the present study. They constitute the so-called "VIRGO'' subsample.
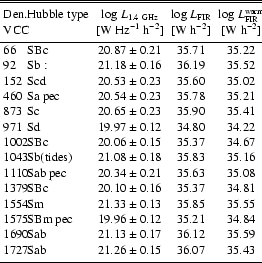
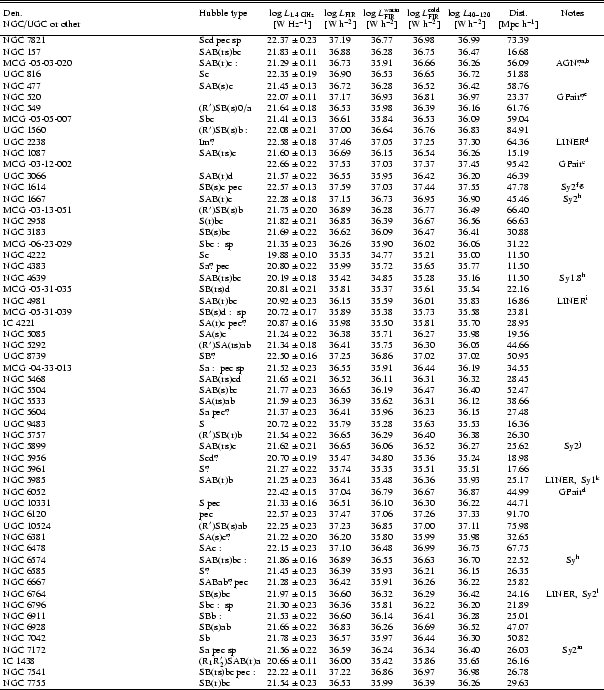
Table 1 reproduces the parameters relevant to this investigation
for the individual VIRGO objects as follows:
Column 1: VCC denomination.
Column 2: morphological type (from the VCC, as in Tuffs et al. 2002,b).
Column 3: total radio continuum luminosity at 1.4 GHz
(
![]() )
with its error (see Appendix A,
only available in the on-line edition of the journal),
in decimal logarithmic units.
)
with its error (see Appendix A,
only available in the on-line edition of the journal),
in decimal logarithmic units.
Column 4: total FIR continuum luminosity (
![]() ),
in decimal logarithmic units.
The uncertainty in this luminosity is
),
in decimal logarithmic units.
The uncertainty in this luminosity is ![]() 15 per cent (random) for
all the sample objects.
15 per cent (random) for
all the sample objects.
Columns 5, 6: FIR continuum luminosities from the warm and cold
dust emission components (
![]() and
and
![]() ), respectively
(from Popescu et al. 2002), in decimal logarithmic units.
We adopt a conservative value of 20 per cent (random) for the uncertainty
of each of these luminosities for all the sample objects.
), respectively
(from Popescu et al. 2002), in decimal logarithmic units.
We adopt a conservative value of 20 per cent (random) for the uncertainty
of each of these luminosities for all the sample objects.
Column 7:
L40-120, i.e., the FIR luminosity that IRAS would have
derived based on the Helou et al. (1988) formula:
![]() ,
where
,
where
![]() and
and
![]() are expressed in Jy.
The luminosity is given in decimal logarithmic units.
We adopt a conservative value of 30 per cent for the uncertainty of this
luminosity for all sample objects.
are expressed in Jy.
The luminosity is given in decimal logarithmic units.
We adopt a conservative value of 30 per cent for the uncertainty of this
luminosity for all sample objects.
Column 8: individual notes.
Luminosities are determined by assuming that all the galaxies
have the same distance of
11.5 h-1 Mpc (Binggeli et al. 1993),
where h is the Hubble constant in units of
100 km s-1 Mpc-1.
|
A sample of 115 nearby galaxies was presented by Stickel et al. (2000)
as a first result of the "ISOPHOT 170 ![]() m Serendipity Survey''
(ISS).
We refer the reader to these authors for details about observations,
data reduction, estimate of the calibration uncertainty, procedure
of extraction of photometry and optical/FIR identification.
m Serendipity Survey''
(ISS).
We refer the reader to these authors for details about observations,
data reduction, estimate of the calibration uncertainty, procedure
of extraction of photometry and optical/FIR identification.
As recognised by Stickel et al., several of their objects have Seyfert/LINER activity and/or are pair/multiple/merging systems.
Not all galaxies from the ISS catalogue could be used in the present
study. Out of the 115 ISS galaxies we first rejected 3 not having IRAS
detections at both
60 and 100 ![]() m and 13 galaxies which either have no morphological
information or are classified as S0, elliptical or peculiar. Of the
remaining 99 galaxies we omitted 3 already included in the VIRGO subsample.
Furthermore, 26 galaxies of the remaining 96 did not have a radio
counterpart or were confused in the NVSS at 1.4 GHz. Radio
counterparts are
associated with optically catalogued galaxies when the distance of the
peak radio surface brightness of the potential radio identification from
the optical position of the target galaxy is within the NVSS resolution.
Furthermore, one galaxy was dropped because it has an inclination greater
than
m and 13 galaxies which either have no morphological
information or are classified as S0, elliptical or peculiar. Of the
remaining 99 galaxies we omitted 3 already included in the VIRGO subsample.
Furthermore, 26 galaxies of the remaining 96 did not have a radio
counterpart or were confused in the NVSS at 1.4 GHz. Radio
counterparts are
associated with optically catalogued galaxies when the distance of the
peak radio surface brightness of the potential radio identification from
the optical position of the target galaxy is within the NVSS resolution.
Furthermore, one galaxy was dropped because it has an inclination greater
than ![]() 70
70![]() and an apparent major axis
longer than
and an apparent major axis
longer than ![]() 4
4![]() .
As discussed in Appendix B
(only available in the on-line edition of the journal),
such galaxies may have flux densities overestimated by a factor of 2.
Finally, only galaxies with heliocentric velocities higher than
1500 km s-1 are selected.
The reason is as follows.
For most of the galaxies in the ISS catalogue only kinematical distances
are available from individual redshifts, as listed by Stickel et al. (2000).
The assumption of a free Hubble Flow does not apply to
the relatively nearby galaxies.
Hence 11 galaxies which are not members of the Virgo Cluster
and have heliocentric velocities lower than 1500 km s-1 were dropped from the sample.
.
As discussed in Appendix B
(only available in the on-line edition of the journal),
such galaxies may have flux densities overestimated by a factor of 2.
Finally, only galaxies with heliocentric velocities higher than
1500 km s-1 are selected.
The reason is as follows.
For most of the galaxies in the ISS catalogue only kinematical distances
are available from individual redshifts, as listed by Stickel et al. (2000).
The assumption of a free Hubble Flow does not apply to
the relatively nearby galaxies.
Hence 11 galaxies which are not members of the Virgo Cluster
and have heliocentric velocities lower than 1500 km s-1 were dropped from the sample.
Hereafter we refer to the final 58 galaxies selected
from the ISS catalogue as the ISS subsample.
For all galaxies in the ISS subsample we determined new warm and
cold dust temperatures from the composite IRAS and ISOPHOT data listed by
Stickel et al. using the method described in Popescu et al. (2002).
For this purpose we first applied ISO/IRAS corrections for the original
IRAS flux densities at 60 and 100 ![]() m and ISO/DIRBE corrections
for the ISOPHOT flux densities at 170
m and ISO/DIRBE corrections
for the ISOPHOT flux densities at 170 ![]() m, both corrections being
taken from Tuffs et al. (2002,b). The SEDs of all these objects
required both warm and cold dust emission components to be fitted.
m, both corrections being
taken from Tuffs et al. (2002,b). The SEDs of all these objects
required both warm and cold dust emission components to be fitted.
We assigned distances to the members of the ISS subsample as follows.
We identify 3 galaxies from the ISS subsample as members of the Virgo
cluster (and not in the ISOPHOT Virgo Cluster Deep sample) and, thus, we
assign them to be at the common distance of
![]() adopted
for the VIRGO subsample (cf. Sect. 2.1).
For the other galaxies of the ISS subsample
we have no clue whether they belong to the field
or to a group/cluster, though we know if they are mergers or not.
We determine kinematical distances, corrected to the Galactic Standard
of Rest with the NED Velocity Correction Calculator, independent of
whether they are isolated or not and whether they are mergers or not.
adopted
for the VIRGO subsample (cf. Sect. 2.1).
For the other galaxies of the ISS subsample
we have no clue whether they belong to the field
or to a group/cluster, though we know if they are mergers or not.
We determine kinematical distances, corrected to the Galactic Standard
of Rest with the NED Velocity Correction Calculator, independent of
whether they are isolated or not and whether they are mergers or not.
Table 2, only available in the on-line edition of the journal,
reproduces the parameters relevant to this investigation
for the individual ISS objects as follows:
Column 1: galaxy denomination (from Stickel et al. 2000).
Column 2: morphological type (from NED).
Column 3: total radio continuum luminosity at 1.4 GHz
(
![]() )
with its error (see Appendix A,
only available in the on-line edition of the journal),
in decimal logarithmic units.
)
with its error (see Appendix A,
only available in the on-line edition of the journal),
in decimal logarithmic units.
Column 4: total FIR continuum luminosity (
![]() ),
in decimal logarithmic units.
The uncertainty in this luminosity is
),
in decimal logarithmic units.
The uncertainty in this luminosity is ![]() 15 per cent (random) for
all the sample objects.
15 per cent (random) for
all the sample objects.
Columns 5, 6: FIR continuum luminosities from the warm and cold dust
emission components (
![]() and
and
![]() ), respectively (this work),
in decimal logarithmic units.
We adopt a conservative value of 20 per cent (random) for the uncertainty
of each of these luminosities for all the sample objects.
), respectively (this work),
in decimal logarithmic units.
We adopt a conservative value of 20 per cent (random) for the uncertainty
of each of these luminosities for all the sample objects.
Column 7: the IRAS FIR luminosity
L40-120 (calculated as in Table 1),
in decimal logarithmic units.
We adopt a conservative value of 30 per cent for the uncertainty
of this luminosity for all the sample objects.
Column 8: galaxy distance.
Column 9: individual notes.
The relationship between the total (warm + cold) FIR emission,
![]() ,
and the radio continuum emission at 1.4 GHz
for the 72 sample galaxies is reproduced in Fig. 1.
Here the solid line reproduces the linear fit to the data (in log-log)
of equation:
,
and the radio continuum emission at 1.4 GHz
for the 72 sample galaxies is reproduced in Fig. 1.
Here the solid line reproduces the linear fit to the data (in log-log)
of equation:

Figure 1 confirms that there is a tight correlation between
dust and radio continuum emission, extending over three orders of magnitude
in both luminosities.
The total FIR/radio correlation is only slightly non-linear, with a slope
![]() .
We note that a luminosity-luminosity correlation analysis
will be biased towards linearity, because it includes also the scaling
effect due to galaxy size (or mass).
Therefore, it is to be expected that the derived slope is only a lower limit
to the slope that would be obtained from an analysis of
normalised luminosities (see Xu et al. 1994a).
.
We note that a luminosity-luminosity correlation analysis
will be biased towards linearity, because it includes also the scaling
effect due to galaxy size (or mass).
Therefore, it is to be expected that the derived slope is only a lower limit
to the slope that would be obtained from an analysis of
normalised luminosities (see Xu et al. 1994a).
As a comparison, in Fig. 1 we also plot the fit to
the
![]() vs.
L40-120 correlation, which is
the equivalent of what would have been derived from IRAS.
The statistics for this fit are also given in Table 3.
There is an obvious shift of up to 0.4 in
vs.
L40-120 correlation, which is
the equivalent of what would have been derived from IRAS.
The statistics for this fit are also given in Table 3.
There is an obvious shift of up to 0.4 in
![]() ,
which is produced by the inclusion of the cold dust component,
mainly not seen by IRAS.
This shift is more pronounced at the faint end of the correlation,
where the cold dust component is more dominant.
This also leads to a slight increase in non-linearity
when the total FIR luminosity is taken into account instead of
L40-120.
,
which is produced by the inclusion of the cold dust component,
mainly not seen by IRAS.
This shift is more pronounced at the faint end of the correlation,
where the cold dust component is more dominant.
This also leads to a slight increase in non-linearity
when the total FIR luminosity is taken into account instead of
L40-120.
The fact that some galaxies show evidence for mild LINER/Seyfert activity
or are in pair/multiple/merging systems does not seem to affect the shape
of the correlation (not shown).
In fact, we obtain
![]() for the subsample of 20 galaxies
with some activity (Table 3) and
for the subsample of 20 galaxies
with some activity (Table 3) and
![]() for the remainder.
Since accretion powered systems are known not to lie on the FIR/radio
correlation (Sopp & Alexander 1991), this implies that even for the objects
in our sample with some evidence for AGN activity, the FIR emission
is powered by star formation activity and not by accretion
(cf. Rodriguez Espinosa et al. 1987).
for the remainder.
Since accretion powered systems are known not to lie on the FIR/radio
correlation (Sopp & Alexander 1991), this implies that even for the objects
in our sample with some evidence for AGN activity, the FIR emission
is powered by star formation activity and not by accretion
(cf. Rodriguez Espinosa et al. 1987).
Figure 2 reproduces the relationship between the warm FIR luminosity
and
![]() for the 72 sample galaxies.
The slope of the correlation is
for the 72 sample galaxies.
The slope of the correlation is
![]() (see Table 3),
which indicates that the correlation is linear.
(see Table 3),
which indicates that the correlation is linear.
This result differs from the previous one of Xu et al. (1994b), who derived
the warm FIR/radio correlation based on the proportionality between
the IRAS FIR and H![]() emissions.
These authors obtained a non-linear correlation, with the radio-to-FIR
luminosity ratio increasing with luminosity.
One possible explanation for the non-linearity of the correlation obtained
by Xu et al. (1994b) is that the H
emissions.
These authors obtained a non-linear correlation, with the radio-to-FIR
luminosity ratio increasing with luminosity.
One possible explanation for the non-linearity of the correlation obtained
by Xu et al. (1994b) is that the H![]() emission was corrected for
extinction using the same value for all galaxies.
However, if more luminous galaxies suffer from larger amounts of
extinction, then the intrinsic H
emission was corrected for
extinction using the same value for all galaxies.
However, if more luminous galaxies suffer from larger amounts of
extinction, then the intrinsic H![]() emission
at the bright end of the correlation was underestimated by Xu et al.,
and thus the warm FIR emission was also underestimated, producing
the non-linearity of the warm FIR/radio correlation found by these authors.
emission
at the bright end of the correlation was underestimated by Xu et al.,
and thus the warm FIR emission was also underestimated, producing
the non-linearity of the warm FIR/radio correlation found by these authors.
As for the total FIR/radio correlation, the fact that some galaxies show
evidence for mild LINER/Seyfert activity or are in pair/multiple/merging
systems does not seem to affect the shape of the correlation (not shown).
The slope of the correlation for the 20 galaxies with some activity
is
![]() (Table 3).
For the remainder we obtain
(Table 3).
For the remainder we obtain
![]() .
.
The comparison between the warm FIR/radio correlation and the equivalent of the IRAS FIR/radio correlation (plotted with the dashed line in Fig. 2) shows that the shift between the two correlations is much smaller than in the case of the total FIR luminosity. In addition, this shift is constant along the luminosity range spanned by the data. This is to be expected, as the IRAS L40-120 luminosity is dominated by the contribution of the warm dust component, and contains only a small contribution from the cold dust component.
Figure 3 reproduces the cold FIR/radio correlation as obtained
for the whole sample of 72 objects.
We find that the cold FIR/radio correlation is only slightly non-linear
(
![]() ,
see Table 3), similar with what we found for
the correlation between
,
see Table 3), similar with what we found for
the correlation between
![]() and the total FIR luminosity
and the total FIR luminosity
![]() (Fig. 1).
This is no surprise since the cold dust component dominates
the total FIR continuum emission of normal late-type galaxies.
(Fig. 1).
This is no surprise since the cold dust component dominates
the total FIR continuum emission of normal late-type galaxies.
We obtained
![]() (Table 3) for the subsample of 20 galaxies
with some activity (LINER/Seyfert or pair/multiple/merging systems)
and
(Table 3) for the subsample of 20 galaxies
with some activity (LINER/Seyfert or pair/multiple/merging systems)
and
![]() for the remainder.
Thus, the different mix of galaxies does not seem to play
any significant role, as for all correlations presented in this study.
for the remainder.
Thus, the different mix of galaxies does not seem to play
any significant role, as for all correlations presented in this study.
In their study of cold dust in Virgo Cluster galaxies, Popescu et al. (2002) plotted warm and cold FIR/radio correlations based on the ISO measurements for the 13 galaxies in their sample which had corresponding radio data. Although the statistics were poor, there was an indication that the warm FIR/radio correlation might be non-linear, whereas in this paper we obtain a linear slope for our sample of 72 objects. Since the sample presented in this work includes the Virgo galaxies from Popescu et al. (2002), we expect to reproduce the same trend when the fit is only applied to the Virgo galaxies. For this we fitted once again the FIR/radio correlations (for the total FIR emission, as well as for the warm and cold FIR emissions), this time separately for the Virgo and non-Virgo galaxies. In total there are 17 Virgo cluster galaxies, comprising the 14 from the VIRGO subsample and 3 Virgo cluster galaxies detected by ISS but not observed by Tuffs et al. (2002,b). Correspondingly, there are 55 non-Virgo galaxies.
The statistics of the fits are given in Table 3. Indeed, in the case of the warm FIR/radio correlation, there is some indication for a non-linear correlation, while the fit to the non-Virgo sample is linear. Overall, there is a tendency for all correlations to be more non-linear for the Virgo sample than for the non-Virgo sample.
In this context it is appropriate to examine the question of
environmental effects.
Such influence on the FIR emission was not found for the Virgo galaxies
(Popescu et al. 2002; Popescu & Tuffs 2002).
However, the radio emission may be more susceptible to
environmental effects, as the radio emitting medium is less tightly bound
to the disk than the FIR emitting medium.
One could imagine a scenario in which synchrotron halo electrons
are swept away by the ram pressure induced by the relative motion of
the galaxies through the intracluster medium.
Preferentially, such a removal may be more severe for more quiescent
galaxies which have less strongly magnetised halos.
This could induce a non-linearity in the FIR/radio correlation.
However this should only be applicable to galaxies which are entering
the intracluster medium now and therefore we expect only sporadic examples
of this phenomenon.
We conclude that environmental effects play only a secondary role in shaping
the FIR/radio correlation.
The main distinction between Virgo and non-Virgo galaxies is rather
that the former populate the faint end of the correlation,
and are more quiescent.
| Whole galaxy | Galaxies with | Virgo | Non-Virgo | ||
| sample | some activity | galaxies | galaxies | ||
| N=72 | N=20 | N=17 | N=55 | ||
| m | 1.10 | 1.09 | 1.31 | 1.10 | |
|
|
0.03 | 0.07 | 0.12 | 0.06 | |
|
|
c | -18.53 | -18.35 | -26.29 | -18.68 |
|
|
|
1.23 | 2.52 | 4.23 | 2.07 |
|
|
1.35 | 1.67 | 2.29 | 1.05 | |
| 0.13 | 0.14 | 0.15 | 0.12 | ||
| m | 1.03 | 0.96 | 1.27 | 0.98 | |
|
|
0.03 | 0.06 | 0.12 | 0.05 | |
|
|
c | -15.55 | -12.80 | -23.68 | -13.88 |
|
|
|
1.19 | 2.22 | 4.23 | 1.88 |
|
|
1.15 | 1.26 | 2.15 | 0.82 | |
| 0.14 | 0.15 | 0.17 | 0.13 | ||
| m | 1.13 | 1.17 | 1.35 | 1.14 | |
|
|
0.04 | 0.08 | 0.14 | 0.06 | |
|
|
c | -19.43 | -21.85 | -27.03 | -19.93 |
|
|
|
1.40 | 2.91 | 4.74 | 2.07 |
|
|
1.61 | 2.27 | 2.36 | 1.38 | |
| 0.15 | 0.17 | 0.16 | 0.15 | ||
| m | 1.04 | 0.93 | 1.29 | 1.01 | |
|
|
0.03 | 0.06 | 0.10 | 0.05 | |
|
|
c | -16.13 | -12.24 | -25.02 | -15.11 |
| L40-120 |
|
1.12 | 2.04 | 3.65 | 1.86 |
|
|
1.28 | 1.61 | 2.85 | 0.75 | |
| 0.13 | 0.15 | 0.16 | 0.11 |
In the previous section we have, for the first time, quantitatively established the correlation between the FIR and radio emission by including the bulk of the FIR luminosity carried by the cold dust component. Furthermore our measurements at three FIR wavelengths allowed a direct determination of the warm and cold FIR emissions. Consequently, separate relations have been derived for the warm and cold FIR/radio relations. In this section we will discuss each of the correlations in terms of the dependence on the star formation rate (SFR).
Detailed mapping observations in the 40-200 ![]() m range of
nearby galaxies (e.g. Haas et al. 1998; Hippelein et al. 2003) as well as
self-consistent models of the UV/submm SEDs in spiral galaxies
(Popescu et al. 2000) are both consistent with the presence of
locally heated dust in star-forming complexes and of diffuse dust
(Tuffs & Popescu 2003).
The diffuse dust is heated both by non-ionising UV photons
and optical photons (Xu 1990).
Then, the relation between SFR and the total FIR energy output
can be derived from the following equation:
m range of
nearby galaxies (e.g. Haas et al. 1998; Hippelein et al. 2003) as well as
self-consistent models of the UV/submm SEDs in spiral galaxies
(Popescu et al. 2000) are both consistent with the presence of
locally heated dust in star-forming complexes and of diffuse dust
(Tuffs & Popescu 2003).
The diffuse dust is heated both by non-ionising UV photons
and optical photons (Xu 1990).
Then, the relation between SFR and the total FIR energy output
can be derived from the following equation:
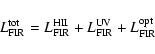 |
(1) |
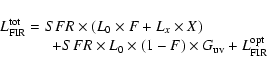 |
(2) |
In the way it is defined (see also Popescu et al. 2000), the F factor accounts for the inhomogeneities in the distributions of dust and stars. It determines the additional likelyhood of absorption of non-ionising UV photons due to correlations between an inhomogeneous distribution of young stars and (opaque) parent molecular clouds. In this sense the F factor represents a clumpiness factor in galaxies.
The value of
![]() depends on both the overall amount of diffuse dust
and its geometrical distribution relative to the distribution of
the young stellar population.
The relative distribution of stellar emissivity and dust as a function of
SFR is not known.
But broadly speaking one would expect SFR to increase with the gas surface
density in galaxy disks (Schmidt 1959; Kennicutt 1998).
If the dust content is proportional to the gas content
depends on both the overall amount of diffuse dust
and its geometrical distribution relative to the distribution of
the young stellar population.
The relative distribution of stellar emissivity and dust as a function of
SFR is not known.
But broadly speaking one would expect SFR to increase with the gas surface
density in galaxy disks (Schmidt 1959; Kennicutt 1998).
If the dust content is proportional to the gas content![]() , the dust opacity would also increase with SFR
(for a fixed geometry).
, the dust opacity would also increase with SFR
(for a fixed geometry).
![]() would then increase with SFR for the optically thin case
and would tend asymptotically towards the fixed value of unity
for the optically thick case.
From this definition it is obvious that the
would then increase with SFR for the optically thin case
and would tend asymptotically towards the fixed value of unity
for the optically thick case.
From this definition it is obvious that the
![]() is a measure of opacity
in galaxies.
is a measure of opacity
in galaxies.
The fraction X of ionising UV photons that are absorbed by dust
in HII regions exhibits a broad range of values, varying from 0.3-0.7 (Inoue et al. 2001; Inoue 2001).
However, even if X approaches unity, the intrinsic luminosity LX is so much smaller than the intrinsic non-ionising UV luminosity L0 (Bruzual & Charlot 1993), that its contribution to
![]() can still be neglected.
can still be neglected.
To interpret the warm FIR/radio correlation, we identify the warm dust
component from our fitting procedure with dust locally heated within
the HII regions, such that
![]() .
In this case
.
In this case
![]() can be written as:
can be written as:
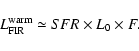 |
(3) |
If the cold dust component is identified with diffuse dust heated by
the interstellar radiation field, then:
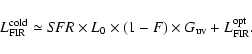 |
(4) |
We have seen in the previous section that it is not easy to identify a scenario which can simultaneously account for both the warm and cold FIR/radio correlations. Whereas the warm FIR/radio correlation was consistent with a linear dependence of the radio on SFR, the cold FIR/radio correlation was more readily interpreted in terms of a non-linear dependence of the radio emission on SFR. To reconcile these seemingly conflicting results we need to re-examine the underlying assumptions on which the results were based.
In drawing the conclusion from the warm FIR/radio correlation we assumed that the clumpiness factor (F) is a constant. However, if an increased SFR is accompanied not only by an increase in the number of independent HII regions, but also by a higher probability for further star formation to happen preferentially near already existing HII regions, then the F factor would also increase, as a consequence of the increased blocking capability of the optically thick molecular clouds in the star-forming complex (e.g. Witt & Gordon 1996). This would be expected to occur if star formation is a self-propagating phenomenon, in which preceding generations of stars can trigger the formation of new generations.
Referring again to Eq. (3), we see that, if the clumpiness factor F increases with SFR, then the
![]() increases more rapidly
than linearly with SFR.
In turn, the radio luminosity, which empirically was found to be
proportional to
increases more rapidly
than linearly with SFR.
In turn, the radio luminosity, which empirically was found to be
proportional to
![]() ,
will also increase more rapidly
than linearly.
Qualitatively this is what is needed to bring the warm FIR/radio correlation
into consistency with the cold FIR/radio correlation.
In Eq. (4) the effect of increasing the clumpiness factor F with SFR
would depress
,
will also increase more rapidly
than linearly.
Qualitatively this is what is needed to bring the warm FIR/radio correlation
into consistency with the cold FIR/radio correlation.
In Eq. (4) the effect of increasing the clumpiness factor F with SFR
would depress
![]() .
This, together with the non-linear dependence of the radio on the SFR,
would mitigate the trends introduced by opacity, leading to an increased
ratio radio/cold FIR with increasing SFR.
.
This, together with the non-linear dependence of the radio on the SFR,
would mitigate the trends introduced by opacity, leading to an increased
ratio radio/cold FIR with increasing SFR.
From this discussion we conclude that one possibility to bring into consistency the warm and cold FIR/radio correlations would be to invoke a non-linear dependence of the radio emission on SFR. Such a non-linear dependence could be understood in terms of an increase in the residence time of the synchrotron-emitting electrons with increasing galaxy size, as postulated by Chi & Wolfendale (1990). However, the same trend can also be obtained within the framework of the calorimeter theory, if the radio emission is identified with the sum of diffuse and localised source components. The localised source component is comprised of synchrotron emission from supernova remnants (which account for about 10 per cent of the total radio flux density of galaxies at 1.4 GHz - Lisenfeld & Völk 2000) plus thermal emission from star forming regions. The diffuse component consists of a pure synchrotron emission component, as given by Völk (1989), plus an additional diffuse free-free component. The free-free component arises from the warm ionised medium, as defined by McKee & Ostriker (1977), and its emission is in general much smaller than the synchrotron emission. Nevertheless we expect that the relative contribution of the synchrotron and free-free components to vary with SFR, such that at high SFR the free-free component becomes non-negligible. This is because the filling factor of the warm ionised medium increases with increasing SFR. Since the non-thermal diffuse radio emission is still proportional with SFR (Völk 1989), then the increased fraction of free-free emission with increasing SFR will introduce the non-linearity in the radio emission.
In this paper we have used a physical though qualitative description of the warm and cold FIR/radio correlations. To quantitatively model these correlations we need to derive the dependence on SFR of both the FIR and the radio emissions. From the point of view of the FIR emission, we need to self-consistently analyse the UV to submm SED of each individual galaxy (Popescu et al. 2000; Popescu & Tuffs 2002). In this way the variation of the terms in Eqs. (3) and (4) - clumpiness (the F factor) and opacity (G factor) - with SFR can be derived. From the point of view of the radio emission we need to determine the relative contribution of its components and express them in terms of the SFR. Such a quantitative treatment would throw insights into the physical processes that make normal galaxies the "machines'' they are, ranging from particle accelerators and magnetic field dynamos, to radiative coolants.
In this paper we present the first analysis of the FIR/radio correlation
which incorporates the bulk of the FIR luminosity radiating longwards of
the spectral coverage of IRAS.
For this we constructed a composite sample of normal galaxies measured with
the ISOPHOT instrument on board ISO.
The sample was a combination of the ISOPHOT Virgo Cluster Deep Sample
(Tuffs et al. 2002,b) and of the ISOPHOT Serendipity Sample
(Stickel et al. 2000).
This provided us with a high dynamic range in star formation activity
as well as good statistics.
All galaxies in the composite sample have had their integrated flux
densities measured by ISOPHOT at 170 ![]() m and by ISOPHOT
(Virgo subsample) or IRAS (Serendipity subsample) at 60 and 100
m and by ISOPHOT
(Virgo subsample) or IRAS (Serendipity subsample) at 60 and 100 ![]() m.
The luminosities of the warm and cold dust emission components
were extracted from the available measurements at the three FIR wavelengths.
This allowed us to define the FIR/radio correlation separately for
the warm and cold dust components.
m.
The luminosities of the warm and cold dust emission components
were extracted from the available measurements at the three FIR wavelengths.
This allowed us to define the FIR/radio correlation separately for
the warm and cold dust components.
The inclusion of the cold dust component produces a tendency for the total FIR/radio correlation to become non-linear. We found that the cold FIR/radio correlation is slightly non-linear, whereas the warm FIR/radio correlation is linear. In order to interpret the individual warm and cold correlations in terms of SFR, we identified the warm emission component with dust locally heated within the HII regions, whereas the cold emission component was identified with diffuse dust heated by the interstellar radiation field. Because the effect of opacity in galaxies would introduce a non-linearity in the cold-FIR/radio correlation, in the opposite sense to that observed, both the radio and the FIR emissions are likely to have a non-linear dependence on SFR (for the range of luminosities covered by our sample, which lies below the luminosity range of starburst galaxies). The behaviour of the radio emission can be accounted for by considering the radio emission to be a superposition of a diffuse synchrotron component, a diffuse free-free component and a localised source component.
Acknowledgements
This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
|
The NVSS used the NRAO Very Large Array telescope and covers the sky
north of a declination of -40 degrees at a frequency of 1.4 GHz,
a resolution of
![]() and a limiting peak source
brightness of about 2.5
and a limiting peak source
brightness of about 2.5
![]() (Condon et al. 1998).
Radio counterparts are associated with optically catalogued galaxies
when the distance of the peak radio surface brightness of
the potential radio identification from the optical position of
the target galaxy is within the NVSS resolution.
The probability of finding an NVSS source within
(Condon et al. 1998).
Radio counterparts are associated with optically catalogued galaxies
when the distance of the peak radio surface brightness of
the potential radio identification from the optical position of
the target galaxy is within the NVSS resolution.
The probability of finding an NVSS source within
![]() of an arbitrary position is 0.02.
of an arbitrary position is 0.02.
As a result of this survey a source catalogue has been produced,
which consists of Gaussian model components fitted to the survey images.
If the source is significantly larger than the resolution of the survey
then it may be represented by several of these components.
The fitted parameters are deconvolved from the instrumental resolution
producing source sizes (or upper limits with 99 per cent confidence)
and the integrated flux density of the model.
Error estimates for each of the source parameters are also given.
In addition to the catalogue, a postage stamp server which returns
FITS files of limited regions from the NVSS calibrated images
is available electronically.
The noise level in these images is about 0.5
![]() .
We have decided to extract our own aperture photometry from
these calibrated maps under the consideration that some
of our sample galaxies might have failed the classification criteria
of the NVSS catalogue and/or not be represented by Gaussian model components
at best and/or have unaccounted faint extended emission.
This question is crucial, since the
.
We have decided to extract our own aperture photometry from
these calibrated maps under the consideration that some
of our sample galaxies might have failed the classification criteria
of the NVSS catalogue and/or not be represented by Gaussian model components
at best and/or have unaccounted faint extended emission.
This question is crucial, since the
![]() beam
of the NVSS has a much smaller aperture than the ISOPHOT beam
at 170
beam
of the NVSS has a much smaller aperture than the ISOPHOT beam
at 170 ![]() m (
m (
![]() ).
Aperture photometry was extracted with the task QPHOT
in IRAF
).
Aperture photometry was extracted with the task QPHOT
in IRAF![]() .
.
We plot the comparison between our photometry (y axis) and the NVSS catalogue one (x axis) in Fig. A.1. Here the solid and long-dashed lines represent the 1:1 and 1.25:1 ratios, respectively, while the box delimited by a short-dashed line corresponds to the region zoomed in the enclosed box. As expected, we find that the agreement is excellent for those radio sources which appear unresolved with the NVSS beam but it becomes worse in case of very extended/complex sources. On average, our fluxes are 25 per cent larger than the NVSS catalogue ones.
Four galaxies from the ISOPHOT Virgo Cluster Deep Survey
(Tuffs et al. 2002,b) were also detected by
the ISOPHOT
![]() Serendipity Survey (Stickel et al. 2000).
These galaxies are: VCC 66, 460, 836 and 873, alias NGC 4178, 4293,
4388 and 4402, respectively.
From the comparison of the 170
Serendipity Survey (Stickel et al. 2000).
These galaxies are: VCC 66, 460, 836 and 873, alias NGC 4178, 4293,
4388 and 4402, respectively.
From the comparison of the 170 ![]() m flux densities of
these 4 galaxies it emerges that the values of Stickel et al.
are systematically higher than those of Tuffs et al.,
the difference being significant (a factor of 2) for VCC 836 and 873.
m flux densities of
these 4 galaxies it emerges that the values of Stickel et al.
are systematically higher than those of Tuffs et al.,
the difference being significant (a factor of 2) for VCC 836 and 873.
The absolute calibration is not a reason for this,
since background measurements averaged over the 4 common objects
are the same to within a few per cent.
However the different techniques used to derived photometry may give rise
to differences.
Even for extended sources, the Serendipity Survey photometry is extracted
by fitting circular gaussians to the strip maps, whereas the Virgo sample
photometry is performed by fitting elliptical gaussians.
Thus, one may expect the Serendipity Survey 170 ![]() m fluxes
to be overestimated as inclination gets larger, as indeed it is the case
for the previous 4 galaxies.
In addition, in the Serendipity Survey photometry there is a spread
of 30 per cent for bright sources, due to systematic effects like offset
of source from scan line.
To this must be added random errors for faint sources (10 Jy or less).
The combined uncertainties can be 50 per cent for faint sources
(see Fig. 2 of Stickel et al. 2000).
Finally, compared with Tuffs et al. (2002,b), Stickel et al.
made larger corrections for the loss of signal incurred by
the transient response of the detector to illumination steps -
the so-called "transient correction''.
The multiplicative corrections of Stickel et al. range from 1.1
for a faint source to a factor of 2 for sources of 60 Jy.
By comparison the transient corrections of Tuffs et al.
are 10 to 20 per cent only for the C200 detector.
m fluxes
to be overestimated as inclination gets larger, as indeed it is the case
for the previous 4 galaxies.
In addition, in the Serendipity Survey photometry there is a spread
of 30 per cent for bright sources, due to systematic effects like offset
of source from scan line.
To this must be added random errors for faint sources (10 Jy or less).
The combined uncertainties can be 50 per cent for faint sources
(see Fig. 2 of Stickel et al. 2000).
Finally, compared with Tuffs et al. (2002,b), Stickel et al.
made larger corrections for the loss of signal incurred by
the transient response of the detector to illumination steps -
the so-called "transient correction''.
The multiplicative corrections of Stickel et al. range from 1.1
for a faint source to a factor of 2 for sources of 60 Jy.
By comparison the transient corrections of Tuffs et al.
are 10 to 20 per cent only for the C200 detector.
From this discussion we conclude that the Serendipity Survey photometry
may be overestimated by a factor of 2 for large (i.e., with apparent
major axis longer than ![]() 4
4![]() )
galaxies with inclinations
higher than
)
galaxies with inclinations
higher than ![]() 70
70![]() .
.