Contents

A&A 407, 589-607 (2003)
DOI: 10.1051/0004-6361:20030841

A spectral survey of the Orion Nebula from 455-507 GHz

Glenn J. White1,2,3 - M. Araki4 - J. S. Greaves5 - M. Ohishi 6 - N. S. Higginbottom7


1 - Centre for Astrophysics & Planetary Science, University of Kent, Canterbury, Kent CT2 7NR, UK
2 - Stockholm Observatory, 133 36 Saltsjöbaden, Sweden
3 - Astrophysics Group, The Cavendish Laboratory, University of Cambridge, Madingley Road, Cambridge CB3 OHE, UK
4 - Institute for Physical Chemistry, University of Basel, Klingelbergstrasse 80, 4056 Basel, Switzerland
5 - Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
6 - National Astronomical Observatory of Japan, 2-21-1, Osawa, Mitaka, Tokyo 181-8588, Japan
7 - Department of Physics, Queen Mary & Westfield College, University of London, Mile End Road, London E1 4NS, UK

Received 11 June 2002 / Accepted 22 May 2003

Abstract
The results of a submillimetre wavelength spectral line survey between 455.1-507.4 GHz of the Orion-KL hot cloud core are reported. A total of 254 lines were detected to a main beam brightness temperature sensitivity $T_{\rm mb}~$$\sim$ 1-3 K. The detected lines are identified as being associated with 30 different molecular species or their isotopomeric variants. The strongest line detected was the J = 4-3 transition of the CO molecule. Apart from abundant diatomic rotors such as CO and CS, the spectrum is dominated by SO, SO$_{\rm 2}$ and CH$_{\rm 3}$OH and large organic molecules such as (CH3)2O, CH$_{\rm 3}$CN, C$_{\rm 2}$H$_{\rm 3}$CN, C$_{\rm 2}$H$_{\rm 5}$CN and HCOOCH$_{\rm 3}$ which make up $\sim$72% of the total number of lines; unidentified lines $\sim$13%; and other lines the remaining $\sim$15$\%$ of the total. Rotational temperatures and column densities derived using standard rotation diagram analysis techniques were found to range from 70-300 K, and 1014-10 $^{{\rm 17}}$ cm$^{\rm 2}$ respectively.

Key words: molecules - star formation - molecular cloud

1 Introduction

The chemistry of the Orion-KL molecular cloud core has been better studied than that of any other massive star formation region in the Galaxy (high spectral resolution spectroscopic surveys have been carried out by a number of authors including: 72-91 GHz Johansson et al.1984, 70-115 GHz Turner 1989, 138-151 GHz Lee et al.2001, 150-160 GHz Ziurys & McGonagle 1993, 215-247 GHz Sutton et al.1985, 216-242 GHz Blake et al.1986, 247-263 GHz Blake et al.1987, 257-273 GHz Greaves & White 1991, 330-360 GHz Jewell et al.1989, 325-360 GHz Schilke et al.1997, 342-359 GHz White et al.1986, 334-343 GHz Sutton et al.1995, 607-725 GHz Schilke et al.2001, 780-900 GHz Comito et al.2003, 190-900 GHz Serabyn & Weisstein 1995). Spectral line surveys can provide an unbiased view of the molecular constituents of the gas in star forming regions, and may be used to estimate the physical and chemical environment. We report here the first high spectral resolution survey in the 600 and 650 $\mu$m atmospheric windows between frequencies of 455 and 507 GHz.

2 The data

The spectral line survey was made using the James Clerk Maxwell telescope in Hawaii during October 1993 over the frequency range 455.1-507.4 GHz. This survey extended across most of the two atmospheric transmission windows near 650 and 600 $\mu$m. These windows are bracketed by strong telluric H2O absorption lines, and their transparency is highly dependent on the line of sight water vapour column. The data were collected using the JCMT facility receiver, RxC, operated in double-sideband mode. The adopted "on-source'' position was that of the "hot core'' close to IRc2 ($\alpha$, $\delta$) $_{1950} = 5^{\rm h}~ 32^{\rm m}~46\hbox{$.\!\!^{\rm s}$ }9$, $-5^\circ$ 24$^\prime$23 $^{\prime\prime}$. The pointing accuracy was measured to be good to better than 2 $^{\prime\prime}$rms, from observations of planets and compact calibrator sources used as standards at the telescope.

The half power beam width and main beam efficiencies of the telescope were measured from observations of Mars, Jupiter and Uranus. These ranged from 11 $^{\prime\prime}$and 0.53 at the low frequency end of the spectral region to 10 $^{\prime\prime}$and 0.49 at the upper end of the band. The receiver double sideband system noise temperatures were typically 1000-3000 K. The IF frequency was 3.94 GHz, and the spectra were processed using the JCMT facility 512 MHz bandwidth acousto-optical spectrometer, giving an effective spectral resolution of $\sim$0.6 km s-1.The spectral region was covered by stepping the local oscillator in 100 MHz steps across the whole spectral region - so that any part of the spectrum was redundantly observed at least four times (i.e. at least twice in each sideband - and in many cases more times). Each observation consisted of a 4-10 min integration (total on and off source), which was carried out in a "position-switched'' mode, where the telescope was alternated between the on-source position, and a "reference position'' located 2100 $^{\prime\prime}$to the north. Previous observations of this "reference position'' have shown it to be free of significant molecular emission intense enough to affect the accuracy of the survey. The reference position was checked by position switching the telescope against several other positions that were located more than 10 degrees away from the Galactic Plane - and not known to be associated with the locations of any molecular clouds or enhanced interstellar extinction. The spectra were calibrated channel by channel using the standard JCMT three temperature chopper calibration scheme (hot and cold loads and the atmosphere). Observations of the sideband gains were measured by observations of spectral lines that were present in both sidebands. The main beam brightness temperature noise levels varied from 1-4 K in a 2 MHz channel ($\sim$1.3 km s-1).

During the data reduction, we attempted to recover an estimate of the single-sideband spectrum, using data collected with a double-sideband receiver. A difficulty common to sideband-deconvolution techniques is the uniqueness of the deconvolution given the observational factors such as pointing reproducibility, sideband gain imbalances, variable calibration solutions as sky conditions change and contamination or blending with strong lines (of both terrestrial and extra-terrestrial origin) in the opposite sideband. A deconvolution technique was used that separated out the emission into the individual sidebands. The basis of this technique (which has been widely used by many observers at the JCMT and forms part of the facility software - although this paper gives the first description of the algorithm that is used) is to set up a series of linked equations for each channel in the DSB spectrum. The first equation simply describes that the DSB line temperature is the sum of two intensities, one from the upper and one from the lower sideband ($T_{\rm u}$ and $T_{\rm l}$, say). The second equation refers to the same spectral channel but with a shift in the local oscillator setting by $\Delta \nu$: the DSB signal is then the sum of $T_{\rm u}$ and $T_{\rm (l + 2 \Delta \nu)}$, if we consider the upper sideband to be the frame of reference and the shift to be positive (increased frequency). Similarly we can consider the lower sideband to be the frame of reference, and obtain a third DSB signal that is the sum of $T_{ (u + 2 \Delta \nu)} + T_{\rm l}$. This equation set can be extended as far as desired by taking any of the line frequencies offset by $2 \Delta \nu$ and establishing which upper and lower sideband frequencies contribute to the observed DSB signal. The result is always to establish a set of n equations with (n + 1) variables that are linked to a particular channel of the DSB spectrum. A solution can only be found where one of the T(DSB) is consistent with zero within the noise level of the observations. Since this implies (if there are no absorption lines) that both $T_{\rm u}$ and $T_{\rm l}$ are also zero within the noise, the equation set reduces to (n- 1) unknowns and two known values - hence all n equations can be solved. In the present survey, the local oscillator was stepped in 100 MHz intervals, and the number of equations used per spectral channel was typically 4-5. For several spectrally crowded regions, additional spectra were taken with different local oscillator offsets to improve the reliability of the deconvolution.

Multiple coverage of individual parts of the spectrum provided sufficient redundancy to allow single sideband spectra to be reconstructed. achieving an acceptable solution at most frequencies. The veracity of the technique could also be checked as lines from the lower and upper sidebands move in opposite directions in the DSB spectrum as the local oscillator frequency is stepped (in 100 MHz intervals). The deconvolution technique worked acceptably for more than 98% of the whole spectral range covered, but the remaining $\sim$2% could not be solved because there was no signal consistent with zero in the DSB signal-set. A greater number of solutions could be found by extending the number of linked equations, but since the solutions are already of the form of sums and differences of DSB signals, the noise level will be increased if more differencing is involved. It is also inherent in the technique that there are a choice of solutions (for n equations and (n - 1) unknowns), so we have adopted the minimum SSB results and an initial DSB signal $\leq $2$ \sigma$ for the "consistent with zero'' DSB criterion. This minimises the level of spikes and should ensure that temperature solutions are underestimated by less than $\approx $3$ \sigma$. The locations of the parts of the spectrum for which we did not achieve a good deconvolution, are shown as horizontal bars under the spectrum in Figs. 3-6. We also visually inspected at the locations in a spectrum where bright lines from the opposite sideband might have left small residual artifacts (sometimes known as "ghost features'' - Schilke et al.1997), as well as inspecting the emission in the opposite sideband to the locations of all of the "U-lines''.  


  \begin{figure} \par\includegraphics[width=15.2cm,clip]{h3757fig1.eps}\end{figure} Figure 1: The complete spectrum binned in 2 MHz channels in main beam brightness temperature units. A low order polynomial baseline was removed from some of the individual spectra. The atmospheric emission spectrum that is overlaid above the Orion spectrum is purely illustrative, and just shows the main features of the atmospheric emission. Recent observational and modeling studies of the terrestrial atmospheric emission (see for example Naylor et al.2000; Pardo et al. 2001a) using collisional parameters extracted from the HITRAN database with an independent radiative transfer model (ATM) and different assumptions about line shapes produce broadly similar atmospheric emission spectra to the one shown here.

3 Data analysis

The intention of this paper is to present the data and some basic results. The spectrum shown in Fig. 1 is crowded with many blended lines, and in many places is confused - reflecting the rich and complex chemistry. A total of 254 lines were identified, although there may be more lines than this blended together. The lines were clearly identified using the JPL Sub-millimetre spectral line catalogues of Pickett et al.(1995), Pearson et al.(1996, 2000), Müller $\rm et~al.$ (2000) and other lists of line frequencies referred to later in this paper. A total of 98 lines (32% of the total) could not be associated with known molecular transitions and have been designated as U-lines. Although it is possible that some fraction of these may be artifacts of the deconvolution process - the fact that they are distributed throughout the survey, and do not tend to congregate in areas where the deconvolution process was not successful, it is likely that many of these are real. Table 1 gives a breakdown of the number of transitions observed from each of the known species.


   
Table 1: JCMT Orion spectral line survey.

Molecule		 $N_{\rm col}~$ Error $T_{\rm rot}~$ Error Number Note
  cm-3 cm-3 K K of lines  
(CH3)2O $1.4\times 10^{16}$ $1.8\times 10^{15}$ 157 30 27(26) lines  
C2H3CN $3.0\times 10^{17}$ $3.2\times 10^{17}$ 180 47 13(6) lines [1]
C2H5CN $2.4\times 10^{16}$ $8.4\times 10^{15}$ 150 12 27(23) lines $T_{\rm rot}$ from Sut85
  $8.3\times 10^{15}$ $1.2\times 10^{15}$ 239 12 27(23) lines $T_{\rm rot}$ from Sch01
C2H5OH $5.6\times 10^{16}$ $4.0\times 10^{16}$ 70 - 8(6) lines $T_{\rm rot}$ from Ohi95
  $4.1\times 10^{16}$ $2.3\times 10^{16}$ 264 196 8(6) lines  
CH2NH $2.4\times 10^{15}$ $5.9\times 10^{14}$ 150 - 3(2) lines $T_{\rm rot}$ from HNCO
CH3CN $3.6\times 10^{15}$ $4.2\times 10^{14}$ 227 21 19 lines  
CH313CN $6.0\times 10^{14}$ $2.2\times 10^{14}$ 227 - 2 lines $T_{\rm rot}$ From CH3CN
  $2.9\times 10^{15}$ - 74 - 2 lines  
CH3OH $9.3\times 10^{16}$ $4.8\times 10^{16}$ 599 295 24(23) lines  
H2CO $1.6\times 10^{16}$ - 166 - 2(1) lines $T_{\rm rot}$ from Bla87
H213CO $1.0\times 10^{15}$ $4.0\times 10^{14}$ 166 - 2 lines $T_{\rm rot}$ from Bla87
HC3N $1.5\times 10^{15}$ - 164 - 2 lines  
HCOOCH3 $5.1\times 10^{16}$ $9.5\times 10^{15}$ 301 95 26(24) lines  
HNCO $4.9\times 10^{15}$ $4.0\times 10^{14}$ 150 14 4(3) lines  
NH2CN $3.3\times 10^{15}$ $8.5\times 10^{14}$ 200 - 3 lines $T_{\rm rot} = 200$ (K) Fix
  $1.1\times 10^{16}$ $4.8\times 10^{15}$ 100 - 3 lines $T_{\rm rot}$ = 100 (K) Fix
OCS $9.0\times 10^{16}$ - 106 - 2 lines  
SO $3.3\times 10^{17}$ - 72 - 2(1) lines $T_{\rm rot}$ from Sut95
34SO $1.1\times 10^{16}$ $3.5\times 10^{15}$ 89 43 5(4) lines  
SO2 $1.2\times 10^{17}$ $1.0\times 10^{16}$ 136 9 35(28) lines  
34SO2 $8.5\times 10^{15}$ - 156 - 3(2) lines  
13CS $2.3\times 10^{14}$ - 120 - 1 line $T_{\rm rot}$ from Zen95
30SiO $3.4\times 10^{14}$ - 50 - 1 line $T_{\rm rot}$ from Sut95
CH3CHO $1.1\times 10^{16}$ - 81 - 1 line $T_{\rm rot}$ from Sch97
CI $1.2\times 10^{18}$ - 30 - 1 line $T_{\rm ex}$ from Whi95
CO $3.5\times 10^{18}$ - 200 - 4 lines (1 transition) $T_{\rm rot}$ from Sut95
DCN $1.1\times 10^{14}$ - 200 - 1 line $T_{\rm rot}$ from Bla87
HCOOH $2.2\times 10^{15}$ - 100 - 1 line $T_{\rm rot}$ from Sut95
HDO $3.2\times 10^{16}$ - 164 - 1 line $T_{\rm rot}$ from Bla87
N2O $4.6\times 10^{16}$ - 230 - 1 line $T_{\rm rot}$ from Wri83
NH2CHO $7.5\times 10^{15}$ - 81 - 1 lines $T_{\rm rot}$ from Sch97
NH2D $8.7\times 10^{15}$ - 160 - 1 line $T_{\rm rot}$ from Her88
LTE rotation temperatures and beam averaged $N_{\rm col}~$, estimated using a Boltzmann plot. The $N_{\rm col}~$were determined using the main beam brightness temperature scale, and for species where only one line was measured, we have assumed $T_{\rm rot}~$as described in Col. 7. Notes: Col. 6: A(B) lines represent A: number of assigned lines, B: number of lines included in the fitting. For A lines only, all lines were included in the fitting. [1]: $v_{\rm 2} = 1$ state lines were not included in the fitting, [2]: Energy levels were considered in the v = 1 vibrational state. Errors quoted are all 1$ \sigma$.

These data were used to estimate the rotational temperature, $T_{\rm rot}~$, and column densities, $N_{\rm col}~$, of the various species using the relationship given in Eq. (1).

 \begin{displaymath}\ln\left(\frac{3kc\int{T_{\rm mb}}{\rm d}V}{8{\pi^{3}}{{\mu^{... ...{\rm rot}}\right)}\right)-\frac{{E{_{\rm u}}}}{k{T_{\rm rot}}} \end{displaymath} (1)

where $\int{T_{\rm mb}} {\rm d}V$ is the integrated intensity of the line, S is the intrinsic strength of the transition, Q is the partition function of the molecule and $\mu$ is the dipole moment. The value of ${\mu^{2}}S$ was calculated from the value of the transition intensity listed by Pickett et al. (1995), using Eq. (2).

 \begin{displaymath}{I_{ba}}\left(T\right)=\left(\frac{8{\pi^{3}}}{3hc}\right){\n... ...}}{kT}}}-{{\rm e}^{\frac{{E_{u}}}{kT}}}}{{Q_{rs}}}\right]\cdot \end{displaymath} (2)

The values for $T_{\rm rot}~$ and column densities are summarised in Table 1.

One of the objectives in analysing spectral line survey data is to determine molecular parameters, such as rotation temperatures, column densities etc. The approach commonly adopted has been to use a "rotation diagram'' to estimate these parameters. In this, an optically thin transition produces an antenna temperature that is proportional to the column density in the upper level of the transition being observed. If all transitions are thermalised and the kinetic temperature is known, then a single integrated line intensity and be used to estimate the total column density of the species in question. The rotational temperature diagram is a plot showing the column density per statistical weight of a number of molecular energy levels, as a function of energy above the ground state - in local thermodynamic equilibrium (LTE), this is equivalent to a Boltzmann distribution. A plot of the natural logarithm of the column density, N, divided by the degeneracy g, versus the Energy E of the final state of the level (expressed in units of degrees K) E/k, will lead to a straight line fit with a slope of 1/T, where g is the statistical weight of level u lying at E energy above the ground state, and T is the rotational temperature. This is equivalent to the kinetic temperature in the limit where all of the levels are thermalised.

One problem for the rotation diagram method is that it may underestimate the total column density if some of the lines fitted are optically thick, or LTE conditions do not hold, or if the background radiation is non-negligible (Turner 1991; Goldsmith & Langer 1999; Nummelin et al.2000; Schilke et al.2001). This can be however be addressed by using less abundant isotopomeric variants that allow estimates to be made of the optical depths, and then using these to correct the column density estimates. It has however been widely used in past molecular line survey studies, because of its computational simplicity, and the absence of a need to have observations of an isotopomer. In this paper we give results from the traditional rotation-diagram technique (Table 1), except in cases pointed out in the Table and text where the results may be affected by high optical depth effects. We have examined a number of cases (CH$_{\rm 3}$CN, SO$_{\rm 2}$, OCS, SO, CH$_{\rm 3}$OH and $^{\rm 34}$SO in some detail - see for example Sects. 4.3 and 4.2 - calculating the optically thick and thin total column densities - and found the use of the rotational temperature technique to provide similar column density estimates are quite similar to the rotational diagram values (see for example discussion of opacities in Sect. 4.2). Another indicator as to whether opacity corrections are important, is to look at the rotational temperature diagrams (see Fig. 7), to see whether there are data points that deviate noticeably from a straight line fit - and which may indicate that the line has saturated. Lee et al. (2001) applied this kind of constraint to seven molecules (CH$_{\rm 3}$OH, HCOOCH$_{\rm 3}$, CH$_{\rm 3}$OCH$_{\rm 3}$, C$_{\rm 2}$H$_{\rm 5}$CN, SO$_{\rm 2}$, CH$_{\rm 3}$CN, and H$_{\rm 2}$CO), finding that the majority could to first order be treated using the rotational technique. The issue of opacity will be further discussed in the relevant sections dealing with molecules that may be opaque - where we also conclude that the effects of opacity are minor in the analysis of data from this survey, and that our justification of using the optically thin rotational temperature technique is adequate although there clear examples (Schilke et al.1997, 2001) where opacity corrections are required for CH$_{\rm 3}$OH.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{h3757fig2.eps}}\end{figure} Figure 2: Cumulative spectrum showing the number of lines detected that exceeded some value.

Full details of the detected lines are given in Tables 2-6.

4 Discussion of individual species

Individual spectra are shown in more detail in Figs. 3, 4, 5 and 6, along with identifications of the prominent lines. Previous studies (Blake et al. 1987; Schilke et al.1997, 2001) have shown that there are four characteristic velocity components in Orion spectra: the extended ridge - which is ambient gas in the Orion Molecular cloud ( $v_{\rm lsr}~$$\sim$ 9 km s-1 $~\Delta\nu \sim 4$ km s-1), the compact ridge - which is a compact clump lying about 10 $^{\prime\prime}$south-west of the hot core ( $v_{\rm lsr}~$ $\sim$ 8 km s-1 $~\Delta\nu \sim$ 3 km s-1), the plateau - which which has been identified as the outflow, and is associated with the broadest spectral lines ( $v_{\rm lsr}~$$\sim$ 6-10 km s-1 $~\Delta\nu \sim$ 20 km s-1), and the hot core that lies close to the infrared source IRc2 ( $v_{\rm lsr}~$ $\sim$ 3-6 km s-1 $~\Delta\nu \sim$ 5-10 km s-1). Most of the observed lines show velocities within these ranges, except a few lines which may suffer from blending (e.g. lines at 455.7798, 459.7069, 466.7817, 495.0007, 496.44095, 503.8517, 504.7281 GHz). The superposed dotted line shows the normalised atmospheric absorption (see Fig. 1 caption) under conditions typical for the survey.


 

 
Table 2: JCMT Orion spectral linesurvey.
Frequency Species Transition Peak Width Vel Notes

MHz		     $T_{\rm mb}$ K km s-1 km s-1  

455.160796		 SO2 215,17-214,18 23.2 33.3 8.2  
455.250265 SO2 295,25-294,26 14.8 19.6 6.9  
455.353721 SO2 185,13-184,14 17.6 8.0 5.4  
455.450207 U-line   4.3 9.4    
455.617930 CH3OH 61-50 36.1 10.6 9.1  
455.779855 SO2 113,9-102,8 60.2 13.8 1.6 Blend with C2H3CN
456.271440 CH3OH 181-172 20.2 6.2 8.4  
456.359253 SO2 195,15-194,16 29.5 11.6 4.4  
456.513228 U-line   18.8 4.3    
456.553270 U-line   4.7 16.6   C3H2 220,22-210,21 ?
456.800826 CH3OH 18-2-18-1 12.7 7.9 5.3 Blend with C2H5CN
456.936702 (CH3)2O 153,12-142,13 5.0 9.3 6.9 4 lines blended
457.006904 CH3OH 112-111 23.7 7.6 8.2  
457.248931 CH3OH 19-1-18-2 9.3 15.6 9.9  
457.325926 SO2 165,11-164,12 30.4 11.3 2.2 Blend with C2H3CN
457.381156 SO2 158,8-167,9+158,7-167,10 7.5 14.6 7.8  
457.472642 SO2 175,13-174,14 50.1 11.4 5.2  
457.584559 U-line   7.0 3.5    
457.637840 U-line   3.5 7.3    
457.723839 C2H5CN 518,44-508,43 5.1 5.2 11.5  
457.736126 HCOOCH3 403,37-393,36 9.2 6.0 7.4  
457.783725 U-line   13.3 9.4    
457.822031 U-line   9.1 28.5    
457.839618 U-line   4.7 4.3   SO2 v2 = 1 ?
457.878236 C2H5CN 532,52-522,51 5.4 4.3 5.2  
457.890562 C2H5CN 285,23-274,24 5.9 6.0 9.3  
457.947140 HCOOCH3 386,32-375,32 3.4 6.0 10.5  
457.985674 HCOOH 203,17-193,16 3.8 2.8 9.6  
458.022659 C2H5CN 484,45-473,44 4.9 10.3 7.2  
458.148139 CH3OH 101-92 15.3 7.0 7.0  
458.276916 (CH3)2O 251,24-242,23 11.6 3.9 8.8 4 lines blended
458.389953 SO2 155,11-154,12 40.8 25.2 6.9  
458.433457 C2H5OH 281,28- 271,27 8.2 5.3 6.1  
458.512326 HCOOCH3 41 2/3/2/2,39-40 3/3/2/2,38 20.7 12.2 8.5 4 lines blended
458.536360 SO2 145,9-144,10 34.8 16.7 5.9  
458.601426 HCOOCH3 3611,25-3511,24 7.1 8.0 9.9  
458.619675 SO2 315,27-314,28 8.6 9.8 3.8  
458.998198 CH3CN J=25-24 K = 9 3.9 5.7 7.3  
459.054419 U-line   20.5 22.1    
459.076694 SO2 135,9-134,10 36.0 14.1 5.0  
459.150830 CH3CN J = 25-24 K = 8 4.3 11.2 4.9  
459.257959 U-line   23.3 24.2    
459.378018 U-line   8.3 6.1    
459.395715 CH3CN J=25-24 K = 6 17.7 10.4 5.4 Blend with CH313CN J=25-24 K =3
459.443401 CH313CN J=25-24 K = 2 4.7 13.9 9.6  
459.492742 CH3CN J=25-24 K =5 20.4 16.7 5.3 Blend with CH313CN J=25-24 K = 0,1
459.511802 NH2CN 23 4,20/19-22 4,19/18 16.0 9.3 9.0  
459.534263 SO2 115,7-114,8 39.4 19.7 5.2  
459.569872 CH3CN J=25-24 K =4 17.3 13.6 6.6  
459.631405 CH3CN J=25-24 K =3 30.9 13.0 6.6  
459.678274 CH3CN J=25-24 K =2 37.8 10.8 4.8  
459.706888 CH3CN J=25-24 K =0,1 35.4 15.5 3.3 2 lines blended
459.760261 HNCO 211,21-201,20 14.8 7.2 6.1  
459.801217 SO2 95,4-94,5+95,5-94,6 35.0 22.8 8.1  
459.881164 SO2 85,3-84,4+85,4-84,5 49.9 32.7 7.6  
459.942528 SO2 75,3-74,4 57.9 26.2 4.8  
459.983548 SO2 55,0-54,1+55,1-54,2 53.6 25.6 11.4  



 

 
Table 3: JCMT Orion spectral linesurvey.
Frequency Species Transition Peak Width Vel Notes

MHz		     $T_{\rm mb}$ K km s-1 km s-1  

460.069658		 C2H5CN 314,27-303,28 2.6 23.5 7.3  
460.214973 HCOOCH3 376,31-366,30 6.5 3.6 8.8  
460.272941 34SO2 64,2-53,3 7.5 31.1 7.8  
460.281266 HCOOCH3 431,43-421,42 8.8 6.9 9.6  
460.306531 C2H5CN 2215,7/8-23 14,10/9 4.0 2.3 7.1  
460.387575 HCOOCH3 3712,26-3612,25 3.1 27.3 8.0 2 lines blended
460.466108 U-line   3.0 13.7    
460.545686 U-line   6.2 6.2    
460.591671 U-line   5.0 3.9    
460.878573 CH3OH 92-81 24.4 6.6 7.3  
460.913504 U-line   3.8 5.0    
461.040768 CO J = 4-3 182.0 51.0 9.0  
461.342825 U-line   5.0 7.5    
461.373909 HNCO 212,19-202,18 7.4 6.1 5.7  
461.709888 HCOOCH3 307,24-296,23 5.5 8.4 9.6  
461.756285 CH3OH 150-141 43.8 11.8 7.8  
461.880198 SO2 209,11-218,14+209,12-218,13 7.9 12.6 6.2  
461.910483 OCS J=38-37 18.1 11.8 7.2  
462.035190 CH3OH $v_{\rm t} = 1$ 106-115+ 8.1 13.0 9.8  
462.036358 C2H5OH 135,9-124,8 8.1 13.0 12.5 Blended with CH3NC
462.138660 HCOOCH3 3711,27-3611,26 3.5 7.0 8.4  
462.236037 34SO   42.0 19.3    
462.334032 13CS J=10-9 14.6 16.4 6.8 Blended with C2H5CN
463.017334 SO2 122,10-111,11 21.3 23.0 5.2  
463.122260 HNCO 211,20-201,19 8.5 6.8 7.2  
463.329490 SO2 354,32-353,33 5.6 14.3 6.9  
463.720861 HC3N J=51-50 8.2 13.2 5.4  
463.836119 34SO2 260,26-251,25 8.2 10.4 9.1  
464.026804 U-line   6.8 25.2    
464.091929 34SO NJ=1111-1010 20.8 25.8 11.6  
464.200231 CH3CHO 74,4-63,3 4.2 5.8 7.9 Blend with HCOOCH3
464.200231 HCOOCH3 3710,28-3610,27 4.2 5.8 9.5 Blend with CH3CHO
464.293855 SO2 335,29-334,30 4.1 10.8 5.1  
464.570359 CH2NH 71,6-61,5 4.4 16.8 8.5  
464.730426 U-line   12.9 6.6    
464.837513 CH3OH 92-91 34.0 11.3 7.2 Blend with C2H5CN 92-91
464.928173 HDO 10,1-00,0 33.5 16.2 6.6  
465.061222 C2H3CN 522,49-492,48 v2 = 1 1.9 11.1 12.3  
465.078910 U-line   3.6 4.1    
465.352350 34SO NJ=1112-1011 30.5 23.0 7.2  
465.512820 U-line   2.4 5.4    
465.543972 (CH3)2O 213,19-202,18 3.6 11.2 5.9 4 lines blended
465.565977 HCOOCH3 361,35-351,34 2.4 14.7 9.0  
465.605514 C2H5CN 52 12,41/40-51 12,40/39 4.0 11.2 4.4  
465.628191 SO2 292,28-291,29 13.0 8.4 5.1  
465.713762 C2H5CN 515,46-505,45 7.4 13.2 5.9  
465.732611 NH2CHO 221,21-211,20 16.1 9.7 6.7  
465.758340 SO2 260,26-251,25 45.3 15.8 4.4  
465.882288 (CH3)2O 144,11-133,10 4.0 9.9 6.1 Blend with SO2
465.882288 SO2 2510,16-269,17+2510,15-269,18 4.0 9.9 8.7 Blended with (CH3)2O
465.922779 SO2 v2 = 1 185,13-184,14 2.2 9.5 7.9  
465.956339 30SiO J=11-10 7.7 15.1 8.8  
466.781659 C2H3CN 49 13,36/37-48 13,35/36 v1 = 1 13.8 30.7 11.9 Blended with C2H5CN
466.781659 C2H5CN 528,44-518,43 13.8 30.7 3.8 Blend with C2H3CN
466.892775 SO2 406,34-405,35 5.5 5.5 5.7  
466.999547 U-line   3.1 5.6    
467.048535 HCOOCH3 38 23,16/15-37 23,15/14 5.6 14.7 8.9  



 

 
Table 4: JCMT Orion spectral linesurvey.
Frequency Species Transition Peak Width Vel Notes

MHz		     $T_{\rm mb}$ K km s-1 km s-1  

467.212513		 HCOOCH3 3822,17-3722,16 4.6 5.5 8.6  
467.282605 C2H3CN 49 16,33/34-48 16,32/33 v1 = 1 6.9 7.6 8.2  
467.318607 HCOOCH3 396,34-386,33 3.9 19.2 9.4 2 lines blended
467.475284 U-line   10.5 8.3    
467.532613 (CH3)2O 260,26-251,25 6.2 5.4 7.7 4 lines blended
467.586402 HCOOCH3 395,34-385,33 3.7 10.5 8.3  
467.627790 HCOOCH3 199,10-188,10 2.8 10.2 8.5  
467.658900 U-line   6.0 17.2    
467.670464 C2H5OH 153,12-142,12 10.4 6.4 9.4  
467.715623 (CH3)2O 261,26-251,25 14.4 13.0 5.6 4 lines blended
467.765733 13CH3OH 101-91 $v_{\rm t} = 0$,1 7.1 6.4    
468.048223 C2H5CN 550,55-540,54 2.9 12.8 6.5  
468.300479 CH3OH 82-81 20.3 8.4 4.7 Blend with U-line
468.345184 U-line   7.6 6.0    
491.943519 SO2 74,4-63,3 49.4 10.3 3.6  
491.978910 H2CO 71,7-61,6 45.0 13.6 2.6  
492.160626 CI 3P1-3P1 17.9 5.0 9.0  
492.281601 CH3OH 41-30 36.9 10.4 7.2  
492.470010 U-line   5.2 8.5    
492.544658 C2H5CN 55 11,45/44-54 11,44/43 3.5 4.3 5.3  
492.695825 13CH3OH   9.9 4.7 8.1  
492.784191 (CH3)2O 96,4-85,4 20.7 8.4 8.6 8 lines blended
493.260821 C2H5CN 581/0,58-571/0,57 4.4 7.4 6.2  
493.370372 U-line   9.6 11.4    
493.701318 CH3OH 53-42 23.7 11.4 7.6  
493.735068 CH3OH 53-42 29.0 9.3 8.1  
494.460056 NH2D 11,0 - 00,0 10.5 8.6 5.8  
494.484560 CH3OH 72-71 50.8 10.3 7.2  
494.555486 SO2 1327-1228 2.5 4.2 7.6  
494.557464 C2H5CN 557,49-547,48 2.5 4.2 5.4 Blend with C2H5OH
494.557464 C2H5OH 109,1-98,1 2.5 4.2 8.7 Blend with C2H5CN
494.575046 C2H5CN 325,27-314,28 2.6 6.4 9.5  
494.596465 (CH3)2O 289,19-288,20+289,20-288,21 5.7 5.3 7.7 8 lines blended
494.756403 C2H3CN 52 17,35/36-51 17,34/35 v = 0 14.1 17.1 5.2  
494.781464 SO2 123,9-112,10 45.0 26.6 7.9  
494.899521 C2H5OH 283,25-273,24 1.8 10.5 3.1  
495.000693 (CH3)2O 279,18-278,19+279,19-278,20 1.6 15.1 10.9 8 lines blended
495.222806 (CH3)2O 271,26-262,25 7.8 14.4 7.5 4 lines blended
495.486885 HCOOCH3 397,32-387,31 12.5 4.8 7.4  
495.821871 C2H5OH 264,22-253,22 2.1 2.8 3.5  
495.842389 SO2 138,6-147,7+138,5-147,8 9.8 20.5 8.5  
495.979430 (CH3)2O 249,15-248,16+249,16-248,17 8.7 5.8 7.1 8 lines blended with CH3CN
495.979430 CH3CN J=27-26 K = 7 8.7 5.8 7.0 Blend with (CH3)2O
496.107704 CH3CN J=27-26 K = 6 11.5 11.6 4.6  
496.207453 CH3CN J=27-26 K = 5 8.8 13.3 6.6  
496.295793 CH3CN J=27-26 K = 4 13.3 11.1 4.8  
496.361787 CH3CN J=27-26 K = 3 19.2 11.6 5.1  
496.409463 CH3CN J=27-26 K = 2 20.7 12.5 5.0  
496.440950 (CH3)2O 249,15-248,16+249,16-248,17 26.6 17.0 10.9 8 lines blended with CH3CN
495.175350 CH3OH 70-6-1 39.7 10.2 7.7  
496.440950 CH3CN J=27-26 K = 1 26.6 17.0 3.2 2 lines blended, Blend with (CH3)2O
496.518825 H213CO 72,6-62,5 3.1 7.2 6.3  
496.633861 (CH3)2O 219,12-218,13+219,13-218,14 7.0 5.2 8.4 8 lines blended
496.764492 C2H3CN 525,47-515,46 v2 = 1 2.2 14.4 14.1  
496.796267 (CH3)2O 209,11-208,12+209,12-208,13 5.8 3.8 8.4 8 lines blended
496.928524 CH3OH 140-131 16.7 9.2 6.5  
497.051216 (CH3)2O 189,9-188,10+189,10-188,11 7.2 14.8 8.6 8 lines blended



 

 
Table 5: JCMT Orion spectral linesurvey.
Frequency Species Transition Peak Width Vel Notes

MHz		     $T_{\rm mb}$ K km s-1 km s-1  

497.085708		 C2H5OH 97,3/2-86,2/3 3.1 10.4 10.3  
497.119025 H213CO 74,4/3-64,3/2 4.8 6.9 6.6  
497.149132 (CH3)2O 179,8-178,9+179,9-178,10 6.4 7.3 8.5 8 lines blended
497.226494 (CH3)2O 169,7-168,8+169,8-168,9 5.5 4.8 10.4 8 lines blended
497.295820 (CH3)2O 159,6-158,7+159,7-158,8 5.2 3.2 8.1 4 lines blended
497.364091 U-line   3.7 7.0    
497.388286 (CH3)2O 139,4-138,5+139,5-138,6 8.5 10.8 8.4 8 lines blended
497.404849 U-line   4.4 1.5    
497.417697 (CH3)2O 129,3-128,4+129,4-128,5 9.4 8.4 9.4 8 lines blended
497.442262 (CH3)2O 119,2-118,3+119,3-118,4 4.2 9.4 8.3 8 lines blended with HCOOCH3
497.442262 HCOOCH3 4013,28-3913,27 +4015,26-3913,27 4.2 9.4 9.0 2 lines blended with (CH3)2O
497.516476 C2H3CN 601,59-601,60 v = 0 4.8 6.1 6.8  
497.556527 U-line   1.5 9.4    
497.606988 (CH3)2O 243,22-232,21 4.3 2.7 8.5 4 lines blended
497.661575 C2H5CN 563,53-553,52 4.9 6.0 3.5 Blend with CH3CN v = 8
497.661575 CH3CN v8=1 J=27-26 K=4 -l 4.9 6.0 4.9 Blend with C2H5CN
497.734975 CH3CN v8=1 J=27-26 K=3 -l 3.5 4.5 8.8  
497.828685 CH3OH 82-81 - 14.0 9.4 8.7  
497.905738 CH3CN v8=1 J=27-26 K=4 +l 3.6 6.4 5.9  
498.288253 C2H5CN 572,55-562,54 2.2 6.6 5.1  
498.327509 OCS J=41-40 12.6 10.2 6.6  
498.412959 CH3CN v8=1 J=27-26 K=1 +l 6.4 6.8 6.9  
498.431868 34SO2 84,4-73,5 5.9 12.2 10.0  
498.596075 HCOOCH3 417,35-407,34 2.2 8.1 9.2  
498.677131 13CH3OH 82-81 8.5 7.3 4.8  
498.785157 C2H5CN 554,51-544,50 2.0 9.8 4.5  
498.849325 (CH3)2O 164,13-153,12 7.7 7.0 8.5 4 lines blended with HCOOCH3
498.849325 HCOOCH3 425,37-415,36 7.7 7.0 6.8 Blend with (CH3)2O
498.984855 C2H5CN 556,49-546,48 5.4 23.7 12.0  
499.198900 HCOOCH3 435,39-425,38 3.0 6.5 8.1  
499.283980 C2H3CN 204,17-193,16 v1 = 1 3.4 13.9 7.3 Blend with C2H5CN
499.283980 C2H5CN 178,10/9-167,9/10 3.4 13.9 3.4 Blend with C2H3CN
499.367702 (CH3)2O 272,26-261,25 3.9 6.1 7.1 4 lines blended
499.892902 C2H5CN 581/2,57-571/2,56 9.1 8.0 5.4  
499.917085 NH2CN 252,23-242,22 8.1 8.1 8.2 13C34S J=11-10 ?
499.944145 U-line   10.2 9.6    
500.038140 HC3N J=55-54 9.0 7.9 6.8  
500.052075 NH2CN 253,22-243,21 8.0 11.8 4.9  
500.075688 SO2 v2=1 74,4-63,3 3.8 11.5 8.6  
500.364813 C2H3CN 416,35-415,36 v2 = 1 4.9 5.7 6.8  
500.432652 SO2 189,9-198,12+189,10-198,11 20.1 6.0 8.3  
500.457324 C2H5CN 129,3/4-118,4/3 22.3 8.2 2.9  
500.475691 CH2NH 22,1-21,2 18.0 7.5 6.3  
500.637890 C2H5CN 355,31-344,30 5.9 5.1 5.5  
500.661562 SO2 312,30-311,31 9.0 13.3 5.3  
501.087663 C2H3CN 551,55-541,54 v1 = 1 11.7 12.8 10.4  
501.116812 SO2 280,28-271,27 21.5 19.1 3.5  
501.592173 CH3OH 92-91 - 32.9 11.7 7.1  
501.656920 C2H5CN 591/0,59-581/0,58 5.6 8.1 8.2  
501.679997 CH2NH 80,8-70,7 4.4 11.5 9.0  
501.891221 (CH3)2O 303,27-294,26 2.8 12.0 9.1 4 lines blended
502.181627 HCOOCH3 1512,3/4-1411,4/3 4.6 7.0 8.2  
502.303684 N2O J=20-19 3.4 17.4 4.7  
503.018652 (CH3)2O 280,28-271,27 10.4 10.7 7.4 4 lines blended
503.107069 (CH3)2O 281,28-270,27 5.1 5.2 9.2 4 lines blended
503.210868 HCOOCH3 408,32-398,31 2.7 7.6 8.5  
503.518307 HCOOCH3 229,13-218,14 6.2 6.1 7.6  



 

 
Table 6: JCMT Orion spectral linesurvey.
Frequency Species Transition Peak Width Vel Notes

MHz		     $T_{\rm mb}$ K km s-1 km s-1  

503.574370		 C2H3CN 53 14,39/40-52 14,38/39 v = 0 9.5 5.6 7.9 Blend with CH3OH
503.574370 CH3OH 76-85 9.5 5.6 7.5 Blend with C2H3CN
503.707705 HCOOCH3 4126,16-4026,15 3.3 6.8 8.4  
503.836578 C2H5CN 286,23-275,22 3.4 2.1 6.8  
503.851690 SO NJ=1514-1414 8.3 10.9 2.1 Blend with C2H3CN
503.921239 C2H3CN 296,24-295,25 v2 = 1 2.0 7.9 12.5  
504.297599 CH3OH 71-60 34.3 8.9 6.6  
504.413582 C2H3CN 23 6,17/18-23 5,18/19 v2 = 1 2.4 16.2 7.6  
504.510971 SO2 2310,14-249,15+2310,13-249,16 2.4 25.3 9.5  
504.680057 SO NJ=43-12 9.3 26.7 6.8  
504.728059 34SO NJ=1211-1110 20.5 22.4 6.6 Blend with C2H5CN
504.728059 C2H5CN 574,54-564,53 20.5 22.4 -0.6 Blend with 34SO
505.431404 U-line   2.7 7.7    
505.499853 C2H5OH 296,23+286,22 3.5 7.9 9.3  
505.765740 CH3OH 102-101 31.4 10.3 6.8  
505.838107 H2CO 70,7-60,6 47.9 17.5 6.4  
506.157737 CH3OH 111-102 26.0 8.3 6.3  
506.240528 HCOOCH3 41 17,25/24-40 17,24/23+41 17,25/24-40 17,23/24 13.7 25.5 6.5 4 lines
506.253692 34SO NJ=1212-1111 11.0 16.9 7.6  
506.773898 U-line   6.3 10.0    
506.831598 DCN J=7-6 8.7 11.8 6.6  
507.041856 U-line   4.5 5.9    
507.200247 HNCO 231,22-221,21 9.6 10.4 6.1  
507.301540 34SO NJ=1213-1112 24.9 27.8 9.0  
507.337692 SO2 366,30-355,31 4.3 6.9 4.8  
507.383231 C2H3CN 273,24-262,25 v1 = 1 8.7 6.6 6.1  



  \begin{figure} \par\includegraphics[width=16.5cm,clip]{h3757fig3.eps}\end{figure} Figure 3: Spectra and lines detected in the survey. The locations of parts of the spectra that were poorly deconvolved are indicated by horizontal lines placed underneath the spectrum.


  \begin{figure} \par\includegraphics[width=16cm,clip]{h3757fig4.eps}\end{figure} Figure 4: Spectra and lines detected in the survey. The locations of parts of the spectra that were poorly deconvolved are indicated by horizontal lines placed underneath the spectrum.


  \begin{figure} \par\includegraphics[width=16cm,clip]{h3757fig5.eps}\end{figure} Figure 5: Spectra and lines detected in the survey. The locations of parts of the spectra that were poorly deconvolved are indicated by horizontal lines placed underneath the spectrum.


  \begin{figure} \par\includegraphics[width=16cm,clip]{h3757fig6.eps}\end{figure} Figure 6: Spectra and lines detected in the survey. The locations of parts of the spectra that were poorly deconvolved are indicated by horizontal lines placed underneath the spectrum.

4.1 CO

In this survey the CO J = 4-3 transition is the most intense single line, with a full width at half maximum of 40 km s-1and full width at zero intensity of at least 120 km s-1. The peak main beam brightness temperature $T_{\rm mb}~$= 182 K was similar to values that we have previously measured using the JCMT (see for example White & Sandell 1995). The line profile clearly shows a small dip close to its peak, which is probably a self-absorption dip. This has also been reported by Schilke et al.(2001) in the J = 6-5 transition, and was seen in all of our earlier unpublished JCMT spectra in this transition using both the present SIS receiver, as well as the original JCMT 460-490 GHz Indium Antimonide receiver (White $\&$ Padman 1991; Padman $\&$ White 1992). We have made careful checks on the many occasions that we have observed this line with the JCMT, confirming that this dip is not a result of the subtraction of emission located at the off position. Unpublished maps (in preparation) of the spatial distribution of this absorption feature show it to be spatially localised on the hot core, and that larger scale CO emission is spatially extended around the core - meaning that the $T_{\rm mb}~$may overestimate the true kinetic temperature.

4.2 Sulphur monoxide (SO) and sulphur dioxide (SO 2)

The high abundances of sulphur based molecules in the interstellar medium are believed to be in part due to the presence of shocks, that favour the endothermic reactions required to form these molecules. The rotational temperature diagram for SO2 (see Fig. 7) is consistent with previous estimates of the temperature and $N_{\rm col}~$$\!$. The temperature is 136 K, typical of the cooler conditions found in the plateau. The value of $N_{\rm col}~$is estimated to be $9.7\times 10^{16}$ cm-2  in the optically thin limit, increasing to $1.2\times 10^{17}$ cm-2  after making a correction for optical depth. Since our initial assumptions might be that this molecule should almost certainly be moderately optically thick, we ran a model, based on the Sutton et al.(1995) temperature and column density estimate, calculating the expected optical depths for the 35 SO2 lines observed in this survey. One transition has a strong opacity $\tau = 1.46$. The optical depth of all other lines are less than 0.9 and for half of all the detected lines $\tau\leq 0.2$. Therefore the results of the optically thick and optically thin estimates of column density are understandably close to each other. This result is in reasonable agreement with studies using similar beam sizes, by Schilke et al.(2001) ( $N_{\rm col}~$ = $9.7\times 10^{16}$ cm-2 , $T\sim 187$ K for a 12-14 $^{\prime\prime}$ beam) and Sutton et al.(1995) ( $N_{\rm col}~$ = $9.4\times 10^{16}$ cm-2 , $T\sim 99$ K for a 12-14 $^{\prime\prime}$ beam).

We further estimate that the isotopic ratio [SO2]/[34SO2] = 14.1, which is in agreement with previous estimates by Blake et al.(1987) (14-16) and Schloerb et al.1983 (11).  

4.3 Methyl cyanide (CH 3CN), ethyl cyanide (propionitrile) (C 2H 5CN), vinyl cyanide (acrylonitrile) C 2H 3CN)

The J = 25-24 and J = 27-26 lines of methyl cyanide were observed at 459 and 495 GHz respectively. The average LSR velocity of the lines were $\sim$5.6 km s-1and the line widths $\sim$11 km s-1. It is therefore likely that this species traces the hot core. The J = 25-24 k = 7 line (459.276 GHz) could not be assigned due to a strong U-line (459.267 GHz). Lines from the J = 27-26 k = 2 (-1) and k = 3 (+1) transitions were observed at 497.790 and 497.971 GHz respectively, although they were not used in the analysis due to their low intensities. The $N_{\rm col}~$and $T_{\rm rot}~$values for this molecule were $3.5\times 10^{15}$ cm-2 and $\sim$230 K - similar to those estimated by Wilner et al.1994; Sutton et al.1995; Lee et al. (2001). Two lines of the isotopomeric variant CH313CN were also detected. No lines from the v8 = 1 family were identified.

For this molecule, a) $T_{\rm rot}~$was fixed at 227 K, obtained from analysis of the CH$_{\rm 3}$CN line, and b) $T_{\rm rot}~$and $N_{\rm col}~$were calculated from the two observed lines. In this latter case, the value of $T_{\rm rot}~$is reduced to about one third that of CH$_{\rm 3}$CN. We consider that case a) provides a better solution, because of the difficulty of estimating $T_{\rm rot}~$from two lines whose upper state energy levels are very similar to each other. It did not prove possible to identify the J = 25-24 k = 0, 1, 3 lines due to blending with CH3CN. In view of the problems that have previously been encountered in the interpretation of CH3CN lines using an optically thin assumption (Schilke et al.1999; Comito et al.2003), we ran a model to calculate the opacity of the various lines based on the above excitation conditions estimated by Wilner et al.(1994) (obtained with a similar beam size to our study). The largest value of $\tau$ amongst the present lines is estimated to be 0.2, and all other values were $\leq $0.1. Making a correction for the optical depth only increases the value of column density by a few percent - from $N_{\rm col}~$= $3.5\times 10^{15}$ cm-2 to $3.6\times 10^{16}$ cm-2 . We therefore conclude that with few exceptions, the optically thin assumption provides a valid and useful estimate of column density for the transitions observed in this survey.

Thirteen lines of vinyl cyanide and its isotopomeric variant C$_{\rm 2}$H$_{\rm 3}$CN were detected at LSR velocities consistent with the molecules being concentrated in the compact ridge. Line frequencies have been reported by Demaison et al.(1994). 5 lines were tentatively associated with the v15 (out-of-plane bend) = 1 vibrational excited state. However, since the frequencies of the v15 lines have a large error, they were not included in the fitting. We also searched at the expected frequency of the v11 = 2 state, but could not find convincing match. Grain surface reactions are thought to be the main process by which complex nitrogen bearing species are formed, due the high level of hydrogenation. It is not likely that a molecule such as CCCN would pick up the required number of hydrogen atoms to become ethyl cyanide without the intermediate step of adsorption on to a grain, allowing the hydrogenation process to occur. The high temperatures found in the hot core are sufficient to evaporate the molecules from the surface of any grains that drift into the region.

Twenty seven lines of ethyl cyanide were detected, based on line frequencies taken from Pearson et al.(1997) and Pearson (2000). It is expected that many observed lines of this molecule are blended with U-lines, and it was found that the simultaneous estimation of the column density and rotational temperature were difficult, since many of the lines are located very close together on the rotational diagram. To avoid this problem. we have calculated the column densities of C$_{\rm 2}$H$_{\rm 5}$CN for two fixed temperatures, deriving values of $N_{\rm col}~$= $2.4\times 10^{16}$ cm-2 (assuming a temperature of 150 K based on the work of Sutton et al.(1985), or $N_{\rm col}~$= $8.3\times 10^{15}$ cm-2 (assuming a temperature of 239 K based on the work of Schilke et al.(2001). As a result, the best estimates of the column density of the C$_{\rm 2}$H$_{\rm 5}$CN from the present data are in the range $N_{\rm col}~$= 2.4- $0.83\times 10^{16}$ cm-2 . This value is close to that estimated by Schilke et al.(2001) ( $N_{\rm col}~$= $3.1\times 10^{16}$ cm-2 ) with a beam size of 10-12 $^{\prime\prime}$- which is very similar to that of the present survey. By comparison, Sutton et al.(1985) reported $N_{\rm col}~$= $2\times 10^{15}$ cm-2 with a 30 $^{\prime\prime}$beam. Assuming that the emitting region is a core with 10 $^{\prime\prime}$diameter, $N_{\rm col}~$= $1.5\times 10^{16}$ cm-2 , which is in better agreement with the estimate in the present survey value. Similar arguments applied to the methyl cyanide line, to resolve the differences between the column densities from this survey, and the work of Blake et al.(1985) and Schilke et al.(2001), again suggest that the size of the emitting region is $\sim$10 $^{\prime\prime}$.

 

4.4 Cyanamide (NH 2CN)

Three lines of NH$_{\rm 2}$CN were detected. However, it did not prove possible to obtain a reliable $T_{\rm rot}~$from the observed data. Consequently we assumed values of $T_{\rm rot}~$of 100 and 200 K, to make a first estimate of the column densities.

4.5 Carbonyl sulphide (OCS)

Two lines of OCS were detected. The fit for $T_{\rm rot}~$and $N_{\rm col}~$are not very accurate, since the upper state energy levels of the two lines are very similar.

4.6 Methylenimeme (CH 2NH)

Methylenimine is a prolate asymmetric rotor with components of the electric dipole moment along both the a and b molecular axes, with magnitudes 1.325 and 1.53 D, respectively. The nitrogen nucleus produces electric quadrupole hyperfine structure in low-lying transitions. CH$_{\rm 2}$NH is a likely product following the UV irradiation of icy interstellar grain mantles and may be a precursor of other complex organics which may be present in cometary ices (Bernstein et al.1995), and may be a precursor to glycinenitrile and glycine (e.g., Dickerson 1978). Three lines of CH$_{\rm 2}$NH were used in the fitting. It was considered likely that the 22,1-21,2 line was probably blended with a U-line, since the intensity was strong compared with the other two lines.

Using only two lines, it did not prove possible to get a reasonable value for $T_{\rm rot}~$. Hence, in fitting the value of $T_{\rm rot}~$was fixed at 150 K, from observations of HNCO, which has a similar dipole moment (CH$_{\rm 2}$NH $\mu({\rm a})$ = 1.352 D, $\mu({\rm b})$ = 1.530 D, HNCO $\mu({\rm a})$ = 1.602 D, $\mu({\rm b})$ = 1.35 D - from Kirchoff et al. 1973; Hocking et al.1975). The derived column density, $N_{\rm col}~$= $2.4\times 10^{15}\pm1.8\times 10^{14}$ cm-2 , is in reasonable agreement with the column density reported in the detection paper by Dickens et al.(1977) of $N_{\rm col}~$= $6.2 \pm 1.8\times 10^{14}$ cm-2 , based on observations of 5 transitions (three of which were blended with other lines) between 172 and 256 GHz obtained with a larger beam of 23-34 $^{\prime\prime}$.

4.7 Methanol (CH 3OH) and ethanol (C 2H 5OH)

Methanol, CH$_{\rm 3}$OH, is one of the most widely observed molecules in star forming regions. Line frequencies are reported by Xu $\&$ Lovas (1997). Twenty four CH$_{\rm 3}$OH lines were detected with an average velocity of 7.8 km s-1 and line width of 9.9 km s-1 - suggesting that it is likely to be excited in the compact ridge. The high observed abundances of this molecule imply a high abundance of the precursor ion CH $_{\rm 3}^{+}$ which would react with water in a ion-molecule process to form methanol. Two lines of $^{\rm 13}$CH$_{\rm 3}$OH (which were apparently detected at 492.695 and 498.677 GHz) would indicate that the main methanol line may have an opacity of at least 0.7. Schilke et al.(2001) have pointed out the difficulty of applying simple rotational analysis techniques to methanol due to opacity problems. The column densities reported in Table 1 have been should therefore be treated as lower limits. If the 498.677 GHz line is assigned to $^{\rm 13}$CH$_{\rm 3}$OH-A(82-81), the column density of this molecule would be $8.7\times 10^{15}$ cm-2 assuming the rotational temperature is the same as that of $^{\rm 12}$CH$_{\rm 3}$OH (600 K - but note that the error on this is 50%). This would indicate that the [12C]/[13C] ratio $\sim$10 - although this would also decrease if the temperature were substantially less than 600K). Neither the $^{\rm 13}$CH$_{\rm 3}$OH-E(23-2-23-1) line at 503.216 GHz, nor any lines of torsionally excited methanol were identified.

Eight lines of C$_{\rm 2}$H$_{\rm 5}$OH were detected, at a velocity of $\sim$8 km s-1, although only 6 were used in the rotational temperature fitting. Line frequencies are given by Pearson et al.(1996). The lines at 494.899 and 495.821 had line widths that were too broad and narrow respectively, and it is likely that these are blended, or due to other species. For this molecule, we made two fits; a) simultaneously fitting both $N_{\rm col}~$and $T_{\rm rot}~$, and b) $T_{\rm rot}~$was fixed at 70 K (following Ohishi et al.1995), since simultaneous fitting of both $T_{\rm rot}~$and $N_{\rm col}~$led to large uncertainties, and a large $T_{\rm rot}~$.

4.8 Methyl formate (HCOOCH 3)

The line widths and velocities of the HCOOCH$_{\rm 3}$ lines suggest an origin in the compact ridge. Line frequencies are given by Osterling et al.(1999). Lines are seen from both the E- and the A-symmetry states. The high abundance follows directly from the high abundance of methanol whose precursor ion CH$_{\rm 3}$OH $_{\rm 2}^{+}$ reacts with H$_{\rm 2}$CO. The column density we derive is similar to that estimated by Schilke et al.(1997), who have discussed difficulties in assigning an unique rotation temperature for this line.

4.9 Dimethyl ether ((CH 3) 2O)

Dimethyl Ether, (CH$_{\rm 3}$)$_{\rm 2}$O, is one of the few interstellar molecules whose emission lines are affected by the presence of two internal rotors. Line frequencies are reported by Groner et al.(1998). Twenty seven lines were detected in this survey, which were best described by a fit of $N_{\rm col}~$= $1.4\times 10^{16}$ cm-2 and $T_{\rm rot}~$= 157 K for the column density and rotational temperature respectively. These values are close to those found by Sutton et al (1985) toward the compact ridge. The line widths and velocities are consistent with an origin in the compact ridge. The fact that this molecule appears to be far more abundant (from the large number of strong lines) than ethanol leads to the conclusion that the Compact ridge, where these molecules are formed, is rich in hydrogen. The molecule is formed by a similar method to methyl formate except that CH$_{\rm 3}$OH $_{\rm 2}^{+}$ reacts with methanol to form it.

4.10 Formaldehyde (H 2CO)

H$_{\rm 2}$CO is a highly prolate asymmetric top molecule. The rotational temperature of H$_{\rm 2}$CO was fixed at 166 K following Blake et al.(1987). Two lines were associated with this molecule, however an additional line at 491.979 GHz was not included in the fitting, since its velocity appeared to be low (2.6 km s-1). The derived column density is very similar to that estimated by Blake et al.(1987).

4.11 Deuterated water (HDO)

A single transition of HDO was detected at 464.925 GHz. It has a clear hot core line shape with a line width of 16.2 km s-1 and a velocity of 6.6 km s-1. We have attempted to model this line along with the two other lines reported and analysed by Schulz et al.(1991) and Sutton et al.(1985). Pardo et al.(2001b) have recently reported detections of the $J_{\rm Ka,Kb}= 2_{\rm 1,2}$-1 $_{\rm 1,1}$ and 1 $_{\rm 1,1}$-$_{\rm0,0}$ lines in the 850-900 GHz region, which appear to trace the plateau gas, rather than the hot core material which contributes rather more to the other HDO lines observed to date. We therefore estimate values of $3.2\times 10^{16}$ cm-2 and 164 K for $N_{\rm col}~$and $T_{\rm rot}~$respectively, in broad agreement with values reported by Plambeck & Wright (1987) and Jacq et al.(1990). This is as expected from the high abundances observed for molecules such as methanol and methyl formate which require water to be present for their formation. It is thought that both water and deuterated water are formed elsewhere on grains and evaporated from the surfaces in the higher temperature conditions found in the hot core (Beckman et al.1981; Pardo et al.2001b).

4.12 Atomic carbon (CI)

A lower limit on the column density of the CI  ${\rm ^3P_1-^3P_0}$  transition was determined with the treatment of the optically thin line emission given by White $\&$ Sandell (1995). The column density, $N_{\rm col}~$= $1.2\times 10^{18}$ cm-2  is consistent with that of White $\&$ Sandell (1995). Keene et al.(1998) detected the 13CI line toward a position 4$^\prime$south of our pointing position, showing that the main isotopomeric line was optically thin. Consequently we have used the optically thin column density estimate.

4.13 Other molecules

Other detections that are of interest include HCCCN and HNCO (Isocyanic Acid), both with line shapes are typical of the hot core, and with estimated abundance similar to those reported by Schilke et al.(1997).

4.14 Unidentified lines

At total of 33 lines were detected that could not be associated with known spectral lines. We searched carefully in the Cologne Database for Molecular Spectroscopy (Müller et al.2001) and the JPL Molecular Spectroscopy Database, as well as other tables of isotopomeric variants of lines that were present in the survey (e.g. CH$_{\rm 3}$OH and $^{\rm 13}$CH$_{\rm 3}$OH from the laboratory measurements of Anderson et al. 1987, 1990, 1992). Although there were inevitably a number of lines that lay close to some of the U-line frequencies, we also used secondary criteria (line strength predictions from the Cologne database, upper energy state levels, and the presence or absence of other lines from similar levels) to make judgments as to whether lines could be associated with particular species. Six lines that were originally designated as U-lines were associated in this way, however a substantial number of intense lines remain. Assignment of lines to these frequencies is beyond the scope of this paper, and will require a sophisticated modeling effort, combined with U-lines from other published surveys. We note that the number of U-lines inferred from the present survey (33 - or 13% of the total) is similar reported from some other surveys (325-360 GHz $\sim$ 8% Sutton et al.1995), 607-725 GHz $\sim$ 14% (Comito et al.2003).

4.15 Notes on $T_{\rm rot}$ diagrams

Plots used to fit the estimates of $T_{\rm rot}~$or $N_{\rm col}~$are shown in Fig. 7.


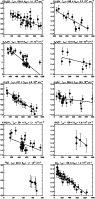  \begin{figure} \par\resizebox{8.3cm}{!}{\includegraphics{h3757fig7.eps}}\end{figure} Figure 7: Rotational temperature diagrams. The fitted lines were derived from a noise-weighted least squares fitting procedure.

The values for the intrinsic line strengths, level degeneracies and partition functions are derived from the literature, including the spectral line catalogues cited previously (see also Eqs. (1) and (2)).

4.16 Line-to-continuum ratio

The data may also be used to estimate the ratio of line-to-continuum emission from the source. This is an important value to characterise for a range of molecular clouds - since a considerable fraction of the fluxes measured with submm continuum cameras, such as the JCMT's SCUBA, and the CSO's SHARC, may be due to the integrated line emission, rather than thermal dust. Early attempts to measure, or characterise this ratio toward Orion have included the work of Groesbeck (1995), Greaves $\&$ White (1991), White $\&$ Sandell (1995), Schilke et al.(1997, 2001). The integrated line emission of the spectrum shown in Fig 1 is $\sim$1.1 $\times$ 105 K MHz. The average rms noise level over the whole survey range was 1.5 K per 2 MHz channel, and therefore line emission would not be detected under this level. If lines of this strength were uniformly spread across the 30 GHz spectral range, then this would contribute a further $\sim$4.5 $\times$ 104 K MHz to the integrated line emission. The total estimated integrated emission corresponds to an integrated main beam temperature of 3.7 K MHz-1. Greaves $\&$ White (1991) reported an integrated emission of $\sim$1.0 $\times$ 104 K MHz over a total range of 16 GHz, which corresponded to an average temperature of 0.6 K MHz-1 - or about one sixth of that estimated here. This discrepancy can partially be explained by the fact that the hot core is smaller in angular extent that the beam size used in both this and the survey of Greaves $\&$ White (1991). The coupling efficiency $\eta_{\rm c}$ to a Gaussian source of radius $\sigma_{\rm s}$ is given by:

 \begin{displaymath}\eta_{\rm c}=\frac{\sigma_{\rm s}^{2}}{\left(\sigma_{\rm s}^{2}+\sigma^{2}\right)} \end{displaymath} (3)

where $ \sigma$ is the Gaussian radius of the telescope beam. Taking $\sigma_{\rm s} = 4$ $^{\prime\prime}$and $\sigma = 4.2$ $^{\prime\prime}$(for a 10 $^{\prime\prime}$FWHM beam), $\eta_{\rm c} = 0.48$, and $\eta_{\rm c} = 0.25$ for the survey of Greaves $\&$ White (1991) would lead to an expectation that the current value should be double that previously estimated for this reason. The lower beam dilution in this survey could explain the rest of the discrepancy. No measurements of the continuum emission exist for the exact frequency that this survey was conducted at, but by using the measurements made by White $\&$ Sandell (1995) at 790 $\mu$m it is possible to extrapolate and make an estimate of the emission at 600 $\mu$m (500 GHz). The spectral index was estimated by White $\&$ Sandell (1995) to be 1.5 and the emission was 134.9 Jy in a 10 $^{\prime\prime}$beam with an aperture efficiency of 0.3. The antenna temperature ($T_{\rm A}$) is given by:

 \begin{displaymath}kT_{\rm A}=\frac{1}{2}\eta_{\rm R}\eta_{\rm A}S_{\nu}A \end{displaymath} (4)

where k is the Boltzmann constant, $\eta_{\rm A}$ is the aperture efficiency (0.3 for these observations), $\eta_{\rm R}$ is the resolution correction and A is the effective area of the antenna. This equation yields a value $T_{\rm A}$ = 6.8K. Correcting this value for sideband gains, atmospheric emission and main beam efficiency gives $T_{\rm mb} = 14.4$ K. This means that the line to continuum ratio at 500 GHz is $3.7\div14.4 = 0.25$. This lies between the value of 10% found by Greaves $\&$ White (1991) and 30-40% found by Sutton et al.(1985) at lower frequencies. We stress that this value is the best estimate lower limit to the line-to-continuum ratio that can be made with the present data - a further measurement that simultaneously measures the continuum and line flux is desirable to obtain a more accurate value - and would for example be valuable when trying to understand the relative contributions of thermal and line emission observed at far infrared wavelengths by bolometer detectors, and far-IR fourier transform spectrometers. The value we have estimated is consistent with the prediction given by Groesbeck (1995 - also reported in Schilke et al.2001) that the contribution of line emission to the total flux of Orion should drop from $\sim$50% at 800 $\mu$m to 10% at 450 $\mu$m.

5 Conclusions

A spectral line survey of the hot core region of the OMC-1 cloud core was obtained over the frequency intervals 455-468 GHz and from 491.8-507.4 GHz.

Acknowledgements

We acknowledge discussions with Prof S. Saito at Fukui University, Dr Y. Fukuyama at the Institute of Physical and Chemical Research, Prof John Pearson, for discussions about frequency assignments of molecules, and the referee for helpful comments.

References


Copyright ESO 2003