Contents

A&A 406, 725-734 (2003)
DOI: 10.1051/0004-6361:20030749

Atmospheric oscillations in solar magnetic flux tubes

II. Excitation by transverse tube waves and random pulses

Z. E. Musielak 1,2 - P. Ulmschneider 2


1 - Department of Physics, University of Texas at Arlington, Arlington, TX 76019, USA
2 - Institut für Theoretische Astrophysik der Universität Heidelberg, Tiergartenstr. 15, 69121 Heidelberg, Germany

Received 20 January 2003 / Accepted 13 May 2003

Abstract
The response of an exponentially diverging magnetic flux tube embedded in an isothermal solar atmosphere to the propagation of transverse tube waves and random transverse pulses generated in the solar convection zone is studied analytically. General solutions are presented and applied to solar flux tubes located in the interior region and at the boundary of supergranulation cells. It is shown that the period of the free oscillations driven by transverse waves and pulses ranges from 7 to 10 min for the considered values of the tube magnetic field, and that these oscillations decay in time as t-3/2. Since the observational signatures of these transverse oscillations are hard to detect, we also consider the generation of longitudinal tube waves by nonlinear mode coupling and the excitation of free atmospheric oscillations by longitudinal waves. Our results show that the basic properties of oscillations driven by transverse and longitudinal tube waves are different. While transverse waves excite oscillations with 7-10 min periods, oscillations by longitudinal waves have periods near 3 min. This is consistent with the observed 3-min oscillations inside the supergranule cells but inconsistent with the 7-min oscillations observed in the chromospheric network. We suggest that an explanation of the observed 7-min oscillations might be found by taking into account a more realistic structure of flux tubes located in the magnetic network.

Key words: Sun: photosphere - Sun: chromosphere - Sun: oscillations - MHD - waves

1 Introduction

In the first paper of this series (Musielak & Ulmschneider 2003, Paper I), we have investigated the excitation of free and forced atmospheric oscillations inside solar magnetic flux tubes by longitudinal tube waves and random pulses. The main obtained results can be summarized as follows. The free atmospheric oscillations with periods near 3 min are always present, independent of the form of the initial disturbance that caused them, and they decay in time as t-3/2 if the frequency of the driving waves is not equal to the cutoff frequency for longitudinal tube waves. The forced atmospheric oscillations represent either propagating or evanescent longitudinal tube waves in an isothermal atmosphere, and they do not decay in time if the wave source drives them continuously. Finally, in the case when the wave frequency is exactly equal to the cutoff frequency, both the free and forced oscillations are the same and they do not decay in time.

Similar results but for acoustic waves have been obtained by Fleck & Schmitz (1993), Kalkofen et al. (1994), Schmitz & Fleck (1995) and Sutmann et al. (1998), and used by these authors to explain the origin of 3 min oscillations observed in the solar chromosphere (e.g., Deubner 1991; Rutten & Uitenbroek1991). These 3 min oscillations are observed in the interior of the supergranulation cells and they can be explained both by processes inside intracell magnetic flux tubes (see Paper I) and outside such structures, where the oscillations are driven by the propagating acoustic waves generated in the solar convection zone (Fleck & Schmitz 1991).

The results obtained in Paper I are also valid for exponentially diverging magnetic flux tubes in the chromospheric network. However, the existence of these tubes at the boundary of supergranulation cells is limited to appropriate regions of the network where enough space is available for the tubes to spread exponentially with height. For such flux tubes, the results of Paper I demonstrate that the propagating longitudinal tube waves and random pulses excite only 3 min oscillations. This is inconsistent with 7 min oscillations observed in the magnetic network (Damé 1983; Lites et al. 1993; Curdt & Heinzel 1998); the periods of these oscillations range from 6 to 15 min and no power is observed at 3 min (e.g., Kalkofen 1996). Therefore, the 7-min oscillations must be of different nature and their origin cannot be explained by the oscillations discussed in Paper I.

Possible explanations of the 7-min oscillations observed in the chromospheric network have been proposed by Deubner & Fleck (1990), who considered formation of standing waves by internal gravity waves, and by Hasan & Kalkofen (1999), who suggested that transverse tube waves generated through buffeting by granules would excite these oscillations. Since the free atmospheric oscillations driven by transverse waves and pulses cannot be directly observed (e.g., Kalkofen 1997), Hasan & Kalkofen suggested that the observed 7-min oscillations are actually excited by longitudinal tube waves generated by transverse tube waves through the process of nonlinear mode coupling (e.g., Ulmschneider et al. 1991). To reach this conclusion, these authors had to asssume that the period of the driven atmospheric oscillations will be preserved after the wave transformation takes place. In this paper, we explore the validity of this assumption after deriving general analytical solutions for the excitation of the free atmospheric oscillations by transverse tube waves and random transverse pulses.

We consider a magnetic flux tube embedded in otherwise non-magnetic and isothermal atmosphere, and assume that this tube is oriented vertically and its magnetic field spreads exponentially with height. In general, the tube supports three different types of waves, namely, longitudinal, transverse, and torsional (e.g., Spruit 1981), and the external medium supports the propagation of acoustic waves. For each wave the corresponding cutoff frequency can be defined, so we have: the longitudinal (Defouw 1976), transverse (Spruit 1982), torsional (Noble et al. 2003), and acoustic (Lamb 1908) cutoff frequency. The tube and the external medium will oscillate with these cutoffs when driven by the corresponding wave motion. The fact that acoustic waves and random acoustic pulses freely propagating in the external atmosphere excite free atmospheric oscillations with the acoustic cutoff frequency has been already well-established (e.g., Fleck & Schmitz 1991; Sutmann et al. 1998). In addition, in Paper I we studied the excitation of free atmospheric oscillations inside the tube by freely propagating longitudinal tube waves and random longitudinal pulses (see also Rae & Roberts 1982). In this paper, we investigate the excitation of tube oscillations with the transverse cutoff frequency by freely propagating transverse tube waves and random transverse pulses (see Spruit & Roberts 1983, and Hasan & Kalkofen 1999, for previous work). Finally, similar studies for torsional oscillations will be described in the next paper of this series.

As mentioned above, the main aim of this paper is to study the excitation of atmospheric oscillations by transverse tube waves and random transverse pulses, which are assumed to be generated in the solar convection zone by turbulent motions interacting with the tube; the most recently computed wave energy spectra carried by transverse tube waves (Musielak & Ulmschneider 2001) are used in our calculations. The presented approach is valid only for exponentially spreading flux tubes, which means that the obtained results can be applied to intracell flux tubes located in the interior of the supergranulation cells and also to those tubes in the magnetic network that can spread exponentially with height. To derive the cutoff frequency for transverse tube waves, we cast the wave equation into a Klein-Gordon form (Sect. 2) and solve it by using a Laplace transformation (Sect. 3). The derived analytical solutions are then applied to solar magnetic flux tubes (Sect. 4). Nonlinear mode coupling is discussed in Sect. 5 and our final conclusions are given in Sect. 6.

2 Klein-Gordon equation and cutoff frequency

A magnetic flux tube is considered to be isolated and embedded in a magnetic field-free, compressible and isothermal medium. The tube is assumed to be thin, untwisted, and oriented vertically, with circular cross-section, and in temperature equilibrium with its surroundings. To describe transverse waves propagating along this tube, we introduce a Cartesian coordinate system with the z-axis being the axis of the non-oscillating tube and the gravity ${\vec g} = - g \hat {\vec z}$, where  $\hat {\vec z}$ is the unit vector along the z-axis. We also consider a local cylindrical coordinate system  $(r, \phi , {\vec l} )$ within the tube, with $\vec l$ being the vector along the tube (Spruit 1981).

The tube magnetic field ${\vec B}_{\rm o} = B_{\rm o} (z) \hat {\vec z}$ is exponentially spreading with height and can be locally expressed as ${\vec B}_{\rm o} = B_{\rm o} ( r, \phi,$ $l ) \hat {\vec l}$, where  $\hat {\vec l}$ is the unit vector along the tube; note that for the non-oscillating tube $\hat {\vec l} = \hat {\vec z}$. Since ${\vec B}_{\rm e} = 0$, the horizontal pressure balance is $p_{\rm o} + B_{\rm o}^2 / 8 \pi = p_{\rm e}$, where $p_{\rm o}$ and $p_{\rm e}$ is the gas pressure inside and outside the tube. In order to distinguish the physical parameters inside and outside the tube, we introduce subscripts "o'' and "e'' to denote the internal and external parameters, respectively. Solar observations show that typical magnetic field inside the tube is $B_{\rm o} = 1500$ G at $\tau_{\rm 5000} = 1$(e.g., Solanki 1993; Stenflo 1994), which is approximately  $B_{\rm o} = 0.85 B_{\rm eq}$, where $B_{\rm eq} = \sqrt{8 \pi p_{\rm e}}$ is the equipartition field. Our model of the exponentially diverging flux tube is valid for isolated intracell fields, for which Wang et al. (1995) found typical magnetic fluxes of $6\times 10^{16}$ Mx. Assuming tube radii of 40 km (Solanki 1993) at the solar surface ( $\tau_{\rm 5000} = 1$) this would imply that the field strength would be similar to that observed in the magnetic network. However, our model is not ideal for crowded flux tubes in the chromospheric network because the exponential expansion of these tubes is prevented by neighboring flux tubes.

We assume that transverse tube waves are excited by the external turbulence alone and that there are no other motions outside or inside the tube. The generated waves are fully described by the perturbations of the tube velocity, ${\vec v} (z,t) = v_{\rm x} (z,t) \hat {\vec x}$, and the magnetic field, ${\vec b} (z,t) = b_{\rm x} (z,t) \hat {\vec x}$; we restrict our consideration to the x-direction only as there is no physical distinction between the x and y directions. Note also that our approach is restricted to linear waves, so that both the density and pressure perturbations can be neglected; this approximation is good for the considered waves in the region of their generation, however, the waves may become nonlinear in higher atmospheric layers due to increasing wave amplitudes with height. The total magnetic field in the Cartesian coordinate system is given by ${\vec B}_{\rm o} = B_{\rm o} (z) \hat {\vec z} + b_{\rm x} (t,z) \hat {\vec x}$, with $b_{\rm x} / B_{\rm o} = l_{\rm x}$.

To derive the wave equation for the velocity perturbation, we linearize the basic MHD equations, use  $\nabla \cdot {\vec v} = 0$ and  $({\vec v} \cdot \nabla ) {\vec v} = 0$, apply the thin flux tube approximation (Musielak & Ulmschneider 2001), and obtain

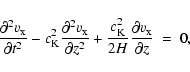\begin{displaymath}{{\partial^2 v_{\rm x}} \over {\partial t^2 }} - c_{\rm K}^2 ... ...over {2 H}} {{\partial v_{\rm x}} \over {\partial z}}\ =\ 0, \end{displaymath} (1)

where the characteristic velocity of these transverse (kink) waves is given by

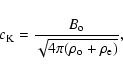\begin{displaymath}c_{\rm K} = {B_{\rm o} \over {\sqrt{4 \pi ( \rho_{\rm o} + \rho_{\rm e} )}}}, \end{displaymath} (2)

and H is the pressure (density) scale height. Note that $c_{\rm K}$ is constant along the tube and, as a result, the form of the derived wave equation is the same for both wave variables.

To remove the first derivative from Eq. (1), we use $v_{\rm x} = v / \rho_{\rm o}^{1/4}$ and obtain

\begin{displaymath}\left [ {{\partial^2 } \over {\partial t^2 }} - c_{\rm K}^2 {... ...ver {\partial z^2 }} + \Omega_{\rm K}^2 \right ] v (z,t) = 0, \end{displaymath} (3)

where $\Omega _{\rm K}$ is the cutoff frequency for transverse tube waves (Spruit 1982)

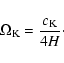\begin{displaymath}\Omega_{\rm K} = {c_{\rm K} \over {4 H}}\cdot \end{displaymath} (4)

The derived wave equation is written in a Klein-Gordon form (see Musielak et al. 1990; Hasan & Kalkofen 1999; Musielak & Ulmschneider 2001), which explicitly displays the cutoff frequency  $\Omega _{\rm K}$. An interesting result is that the form of the wave equation derived here for transverse tube waves is the same as that obtained for longitudinal tube waves in Paper I and for acoustic waves by Sutmann et al. (1998); the only difference is the explicit form of the cutoff freqeuncy for each type of wave.

The characteristic speed $c_{\rm K}$ for transverse tube waves can be expressed in terms of the sound speed $c_{\rm S} = \gamma p_{\rm o} / \rho_{\rm o}$ and plasma $\beta$, where $\beta = 8 \pi p_{\rm o} / B_{\rm o}^2$, as

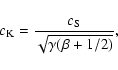\begin{displaymath}c_{\rm K} = {c_{\rm S} \over {\sqrt{ \gamma ( \beta + 1/2 )}}}, \end{displaymath} (5)

which shows that $c_{\rm K}/c_{\rm S} \rightarrow 1.095$ as $\beta \rightarrow 0$ and $c_{\rm K}/c_{\rm S} \rightarrow 0$ as $\beta \rightarrow \infty$. We may now use Eq. (5) of Paper I to eliminate $c_{\rm S}$ from the above equation and relate $c_{\rm K}$ to the characteristic velocity of longitudinal tube waves $c_{\rm T}$. This gives

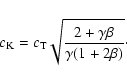\begin{displaymath}c_{\rm K} = c_{\rm T} \sqrt{ {2 + \gamma \beta} \over {\gamma (1+ 2 \beta)}}\cdot \end{displaymath} (6)

For $\beta \rightarrow 0$ we have $c_{\rm K} / c_{\rm T} \rightarrow \sqrt {2 / \gamma} \approx 1.095$ and for $\beta\gg 0$ one finds $c_{\rm K} / c_{\rm T} \approx \sqrt {1 / 2} \approx 0.707$. Hence both characteristic tube speeds are comparable only for low-$\beta$ plasma, otherwise longitudinal tube waves propagate faster than transverse tube waves.

Similar relationships can be found for the cutoff frequency  $\Omega _{\rm K}$, which can be expressed in terms of the acoustic cutoff frequency  $\Omega_{\rm S} = c_{\rm S} / 2 H$ (Lamb 1908) and plasma $\beta$ as

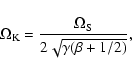\begin{displaymath}\Omega_{\rm K} = {\Omega_{\rm S} \over { 2 \sqrt{\gamma (\beta + 1/2)}}} , \end{displaymath} (7)

and in terms of the cutoff frequency for longitudinal tube waves  $\Omega_{\rm T}$ (Defouw 1976; see also Eq. (4) of Paper I) as

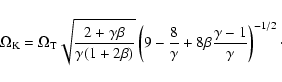\begin{displaymath}\Omega_{\rm K} = \Omega_{\rm T} \sqrt{ {2 + \gamma \beta} \ov... ...} + 8 \beta {{\gamma - 1} \over \gamma} \right )^{-1/2}\cdot \end{displaymath} (8)

According to these equations, $\Omega_{\rm K} / \Omega_{\rm S} \rightarrow \sqrt {2 / \gamma} / 2 \approx 0.548$ and $\Omega_{\rm K} / \Omega_{\rm T} \rightarrow \sqrt {2 / \gamma} / \sqrt {9 - 8/ \gamma} \approx 0.535$when  $\beta \rightarrow 0$, and $\Omega_{\rm K} / \Omega_{\rm S} \rightarrow 0$ when  $\beta \rightarrow \infty$, and $\Omega_{\rm K} / \Omega_{\rm T} \rightarrow 1 / 4 \sqrt {\gamma - 1 / \gamma} \sqrt {\beta} \approx 0.395 / \sqrt {\beta}$ for $\beta\gg 0$. Thus, $\Omega _{\rm K}$ is almost half of $\Omega_{\rm T}$ (or $\Omega_{\rm S}$) for low-$\beta$ plasma and decreases when $\beta$ increases. This means that the range of frequencies for the propagation of transverse tube waves is at least twice as large as the one for either longitudinal tube waves or acoustic waves. Note that  $\Omega _{\rm K}$ and  $\Omega_{\rm S}$ are the only cutoff frequencies in the approach considered in this paper. By making Fourier transform of Eq. (3), one derives the dispersion relation and finds that transverse tube waves are propagating if their frequency $\omega > \Omega_{\rm K}$, otherwise they are evanescent. The cutoff frequency  $\Omega_{\rm S}$ plays the same role for the propagation of acoustic waves in the external medium.

3 Mathematical solutions

The obtained Klein-Gordon equation can be solved by specifying the initial and boundary conditions. We follow Sutmann et al. (1998) and take

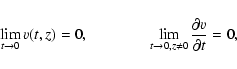\begin{displaymath}\lim_{t\to 0} v (t,z) = 0, \qquad \qquad \lim_{t\to 0, z\ne 0} {{\partial v} \over {\partial t}} = 0, \end{displaymath} (9)


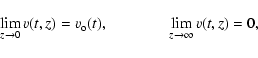\begin{displaymath}\lim_{z\to 0} v(t,z) = v_{\rm o} (t), \qquad \qquad \lim_{z\to \infty} v(t,z) = 0 , \end{displaymath} (10)

where $v_{\rm o} (t)$ is an arbitrary excitation velocity to be prescribed at z=0 inside the tube. These initial and boundary conditions are of the same form as those considered by Sutmann et al. (1998), therefore, their results can be directly used to solve the problem discussed in this paper. As shown by these authors, the general solution can be obtained by performing Laplace transforms and can be written as

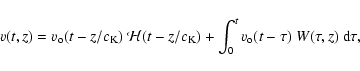\begin{displaymath}v (t,z)= v_{\rm o} (t - z/c_{\rm K})\ {\cal H} (t - z/c_{\rm K}) +\int_0^t v_{\rm o} (t - \tau)\ W (\tau , z)\ {\rm d}\tau, \end{displaymath} (11)

where ${\cal H} (t-z/c_{\rm K})$ is the Heaviside step-function and its value is 0 for $t < z/c_{\rm K}$ and 1 for all values of  $t > z/c_{\rm K}$, while  ${\cal H} (t-z/c_{\rm K}) = 0.5$ if $t = z/c_{\rm K}$. The function $W(\tau,z)$ arises from the inverse Laplace transform (see Sutmann et al. 1998, for details) and is given by

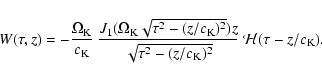\begin{displaymath}W(\tau , z) = - {{\Omega_{\rm K}} \over c_{\rm K}}\ {{J_1 (\... ...qrt{\tau^2 - (z/c_{\rm K})^2}}}\ {\cal H} (\tau-z/c_{\rm K}). \end{displaymath} (12)

To investigate the excitation of the free and forced atmospheric oscillations inside a magnetic flux tube, we consider four different cases, namely, excitation by monochromatic transverse tube waves, a spectrum of transverse tube waves, a $\delta $-function pulse and a wavetrain of random pulses. Similar cases but for acoustic waves have been considered by Sutmann et al. (1998) who derived the general analytical solution for each case. From a mathematical point of view, the basic equations derived here are of the same form as those obtained by these authors. Therefore, their solutions may be formally used here and they only require to replace $c_{\rm S}$ by $c_{\rm K}$ and  $\Omega_{\rm S}$ by  $\Omega _{\rm K}$. It must be noted that the basic mathematical structure of these equations is also the same to that discussed in Paper I for longitudinal tube waves; this means that we could use the results of Paper I and replace $c_{\rm T}$ by $c_{\rm K}$ and  $\Omega_{\rm T}$ by  $\Omega _{\rm K}$. In the next section, we present and discuss the final solutions and used them to study oscillations of magnetic flux tubes in the solar atmosphere.

3.1 Excitation by monochromatic transverse tube waves

We assume that monochromatic transverse tube waves with frequency $\omega$ and amplitude $u_{\rm o}$, is continuously generated by the external turbulent motions (see Sect. 4) and they propagate along the flux tube. The boundary condition (Eq. (10)) that describes this process is

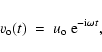\begin{displaymath}v_{\rm o}(t)\ =\ u_{\rm o}\ {\rm e}^{-{\rm i}\omega t}, \end{displaymath} (13)

which allows writing the general solution (see Eq. (27) in Sutmann et al. 1998) as
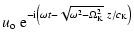                                v (t, z) = $\displaystyle u_{\rm o}\ {\rm e}^{- {\rm i} \left ( \omega t - \sqrt{\omega^2-\Omega_{\rm K}^2}\ z/c_{\rm K} \right )}$  
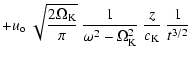    $\displaystyle + u_{\rm o}\ \sqrt{{2 \Omega_{\rm K}} \over {\pi}}\ {{1} \over {\omega^2 - \Omega_{\rm K}^2}}\ {{z} \over {c_{\rm K}}}\ {{1} \over {t^{3/2}}}$  
    $\displaystyle \times \left [ \Omega_{\rm K} \sin \left (\Omega_{\rm K} t - {{3 ... ...mega \cos \left ( \Omega_{\rm K} t - {{3 \pi} \over {4}} \right ) \right ]\cdot$ (14)

The first term on the RHS of this equation describes the forced atmospheric oscillations represented here by either the propagating ( $\omega > \Omega_{\rm K}$) or evanescent ( $\omega < \Omega_{\rm K}$) transverse tube waves (Spruit 1982); note that these oscillations do not decay in time if they are driven by monochromatic waves that are continuously generated. The free atmospheric oscillations are described by the second term on the RHS of Eq. (14) and it is seen that they decay in time as t-3/2 at any given height and their amplitude increases linearly with height (Hasan & Kalkofen 1999). The decay time for these oscillations is the same as that previously found for acoustic waves (Fleck & Schmitz 1991, 1993; Kalkofen et al. 1994; Schmitz & Fleck 1995; Sutmann & Ulmschneider 1995a,b; Sutmann et al. 1998) and for longitudinal tube waves in Paper I.

3.2 Excitation by a spectrum of transverse tube waves

The spectrum of transverse tube waves generated at the lower tube boundary (z=0) is approximated here by a linear superposition of sinusoidal partial waves with different amplitudes, frequencies and phases. The initial velocity  $v_{\rm o} (t)$ required for the boundary condition given by Eq. (10) can be specified as

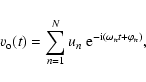\begin{displaymath}v_{\rm o}(t) = \sum_{n=1}^N u_{n}\ {\rm e}^{-{\rm i}(\omega_{n} t + \varphi_{n})}, \end{displaymath} (15)

where un and $\omega_{n}$ are the velocity amplitudes and frequencies of the partial waves, respectively, and  $\varphi_{n}$are arbitrary constant phases. We use Eq. (36) from Sutmann et al. (1998) to write
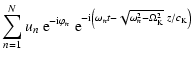                               v (t, z) = $\displaystyle \sum_{n=1}^N u_{n}\ {\rm e}^{-{\rm i} \varphi_{n}}\ {\rm e}^{- {\... ... ( \omega_{n} t - \sqrt{\omega_{n}^2 - \Omega_{\rm K}^2}\ z/c_{\rm K} \right )}$  
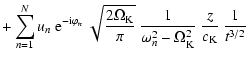    $\displaystyle + \sum_{n=1}^N u_{n}\ {\rm e}^{-{\rm i} \varphi_{n}}\ \sqrt{{2 \O... ...mega_{n}^2 - \Omega_{\rm K}^2}}\ {{z} \over {c_{\rm K}}}\ {{1} \over {t^{3/2}}}$  
    $\displaystyle \times \left [ \Omega_{\rm K} \sin \left (\Omega_{\rm K} t - {{3 ... ..._{n} \cos \left ( \Omega_{\rm K} t - {{3 \pi} \over {4}} \right ) \right ]\cdot$ (16)

Similar to the previous case of monochromatic waves, there are two different types of oscillations, namely, the forced atmospheric oscillations that do not decay in time and the free atmospheric oscillations that decay in time as t-3/2. All partial waves with  $\omega_{n} > \Omega_{\rm K}$ propagate freely along the tube and the waves with  $\omega_{n} < \Omega_{\rm K}$ are evenescent. Each partial wave excites its own free oscillations, which superpose and have amplitudes that decay in time as t-3/2. If $\omega_{n} \rightarrow \Omega_{\rm K}$, then we must take $t \rightarrow \infty$ which makes the second term in Eq. (16) equal zero, and the free and forced oscillations become the same and they do not decay in time.

Excitation by a $\delta $-function pulse

We now consider one transverse pulse with a $\delta $-function shape to be generated at z=0. The required boundary condition is

\begin{displaymath}v_{\rm o}(t^{\prime}) = u_{\rm o}\ \delta (t^{\prime}), \end{displaymath} (17)

where $t^{\prime} = \Omega_{\rm K} t / 2 \pi$.

We follow Sutmann et al. (1998) to obtain

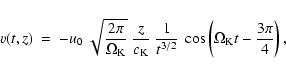\begin{displaymath}v (t, z)\ =\ - u_{\rm0}\ \sqrt{{2 \pi} \over \Omega_{\rm K}}\... ...\cos \left ( \Omega_{\rm K} t - {{3 \pi} \over {4}} \right ) , \end{displaymath} (18)

which shows that only free atmospheric oscillations are excited and that they also decay as t-3/2. The forced oscillations are not present in this case because there is no continuous excitation.

3.4 Excitation by a wavetrain of random pulses

Finally, we assume that a wavetrain of transerse and sinusoidal pulses with randomly chosen amplitudes and periods is generated at the lower boundary of the tube (z=0) and propagates upward along the tube. A new pulse is stochastically chosen after the time equal to the passed wave period of the previous pulse. The boundary condition requires  $v_{\rm o} (t)$ to be given in the following form:

\begin{displaymath}v_{\rm o} (t)\ =\ \sum_{n=1}^\infty u_{n}\ {\rm e}^{-{\rm i}\... ...} t}\ \left[ {\cal H}(t-t_{n-1}) - {\cal H}(t-t_{n}) \right], \end{displaymath} (19)

where un and  $\omega_{n}$ are randomly chosen wave amplitudes and periods, respectively. In addition, we have

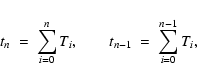\begin{displaymath}t_n\ =\ \sum_{i=0}^{n} T_{i} , \qquad t_{n-1}\ =\ \sum_{i=0}^{n-1} T_{i} , \end{displaymath} (20)

and

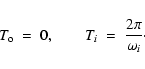\begin{displaymath}T_{\rm o}\ =\ 0 , \qquad T_{i}\ =\ {2 \pi \over \omega_{i}}\cdot \end{displaymath} (21)

Using Eq. (11) and applying the asymptotic limit of $t \gg z/c_{\rm K}$ to Eq. (12), we obtain (see Eq. (62) in Sutmann et al. 1998)

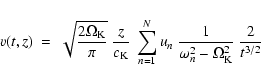
\begin{displaymath}v (t, z)\ =\ \sqrt{2 \Omega_{\rm K} \over \pi}\ {z \over c_{\... ... \over {\omega_{n}^2 - \Omega_{\rm K}^2}}\ {2 \over t^{3/2}}\ \end{displaymath}


\begin{displaymath}\times \left [\Omega_{\rm K} \cos (\Omega_{\rm K} t - \varphi... ... \sin (\Omega_{\rm K} t - \varphi_1)\ \right] \sin \varphi_2, \end{displaymath} (22)

where N is chosen in such a way that t > tN, and

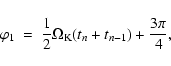\begin{displaymath}\varphi_1\ =\ {1 \over 2} \Omega_{\rm K} (t_{n} + t_{n-1}) + {3 \pi \over 4} , \end{displaymath} (23)


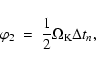\begin{displaymath}\varphi_2\ =\ {1 \over 2} \Omega_{\rm K} \Delta t_{n} , \end{displaymath} (24)

with $\Delta t_{n} = t_{n} - t_{n-1}$.

Similar to the previous case, the wavetrain of random pulses generates only the free atmospheric oscillations because the excitation is not continuous but instead it is stopped at the time t > tN; the latter means that only N pulses are generated. The derived analytical solution shows that these oscillations also decay in time as t-3/2.

4 Application to solar magnetic flux tubes

We compute the structure of the solar atmosphere outside the magnetic flux tube by taking gravity $g = 2.376 \times 10^4$ cm/s2, and assuming that the atmosphere is isothermal with temperature $T_{\rm e} = 5000$ K and extends from z=0 to z=2000 km. The gas pressure outside the tube at z=0 is assumed to be $p_{\rm e} = 4 \times 10^4$ dyn/cm2, which approximately corresponds to  $T_{\rm e} = 5000$ K in the VAL model (Vernazza et al. 1981). The atmosphere inside the tube is also isothermal with  $T_{\rm o} = T_{\rm e}$. We specify the tube magnetic field to be  $B_{\rm o} / B_{\rm eq} = 0.85$ at  $\tau _{5000} = 1$ (see Sect. 2) and use the horizontal pressure balance to calculate the distribution of physical parameters inside the tube with depth and height. Since the value of the tube magnetic field may vary for flux tubes on the Sun (e.g., Solanki 1993), we also consider $B_{\rm o} / B_{\rm eq} = 0.95$ and 0.75 (Ulmschneider & Musielak 1998).

The characteristic tube speed $c_{\rm K}$ and the cutoff frequency  $\Omega _{\rm K}$ are computed for each value of the tube magnetic field and given in Table 1. To compare these values with the sound speed $c_{\rm S}$ and the acoustic cutoff frequency  $\Omega_{\rm S}$, we take $\gamma = 5/3$ and get $c_{\rm S} = 7.3$ km s-1 and $\Omega_{\rm S} = 0.0312$ s-1. Hence, the speed of transverse tube waves is either lower than, or comparable to, the sound speed and this is consistent with Eq. (6) as $B_{\rm o} / B_{\rm eq} = 0.75$, 0.85, and 0.95 correspond respectively to $B_{\rm o} \approx 1325$, 1500, and 1675 G, or $\beta \approx 0.8$, 0.4, and 0.1 at $\tau _{5000} = 1$. The values of  $\Omega _{\rm K}$ is always lower than  $\Omega_{\rm S}$ (see Eq. (7)) and changes with the strength of the tube magnetic field (Table 1).

Note that $c_{\rm K}$, $c_{\rm S}$, $\Omega _{\rm K}$ and  $\Omega_{\rm S}$ are constant in our model because the background atmosphere is isothermal and the tube expands exponentially with height. The cutoff frequencies that are the same in the entire atmospheric model are often referred to as the "global" cutoff frequencies to distinct them from the so-called "local'' cutoff frequencies which vary with height due to the presence of other gradients, for example, the temperature gradient (e.g., Brown et al. 1986); obviously, all cutoff frequencies discussed here and in Paper I are the global cutoff frequencies. In the following, we present the results of our calculations by plotting the real part of the normalized wave velocity  $v (z,t)/ c_{\rm K}$ with time for the free atmospheric oscillation at two different atmospheric heights z=500 and 2000 km; in all our calculations the conditions  $t \gg z/c_{\rm K}$ and $t \gg 1/ \vert \Omega_{\rm K} \pm \omega \vert$ are always fulfilled.


 

 
Table 1: The characteristic velocity $c_{\rm K}$ (km s-1), cutoff frequency  $\Omega _{\rm K}$ (s-1) and total wave energy flux $F_{\rm K}$ (erg cm-2 s-1) are given for three different values of $B_{\rm o}$/ $B_{\rm eq}$ used in this paper. By comparing the maximum wave frequency  $\omega _{\rm max}$ to  $\Omega _{\rm K}$, it is seen that most of the generated wave energy is carried by propagating longitudinal tube waves. The wave energy fluxes are computed by following Musielak & Ulmschneider (2001).
$B_{\rm o}$/ $B_{\rm eq}$ $c_{\rm K}$ $\Omega _{\rm K}$ $\omega _{\rm max}$ $F_{\rm K}$
 0.75 5.0 0.0107 0.0152 $2.2\times 10^8$
 0.85 6.0 0.0129 0.0183 $1.4\times 10^8$
 0.95 7.3 0.0155 0.0220 $8.9\times 10^7$


4.1 Wave energy fluxes

The interaction between a thin and vertically oriented magnetic flux tube and the external turbulent motions has been studied analytically by Musielak & Ulmschneider (2001), who developed a general theory describing the generation of transverse tube waves and used to compute the wave energy spectra and fluxes for the Sun and late-type dwarfs (Musielak & Ulmschneider 2002a,b). Similar to the generation of longitudinal tube waves discussed in Paper I, this theory is also based on the original work done by Lighthill (1952) in which the inhomogeneous wave equation is derived and the source function is assumed to be fully determined by the turbulent motions. To prescribe the source function, one typically uses an extended form of the Kolgomorov turbulent energy spectrum and a modified Gaussian frequency factor given by Musielak et al. (1994); both forms have been adopted by Musielak et al. (1995) to study the excitation of longitudinal tube waves, by Rubinstein & Zhou (2002) to investigate the generation of acoustic waves, and by Bi & Xu (2002) to examine the efffects of turbulence on the solar p-mode oscillations.

We follow Musielak & Ulmschneider (2002a) to calculate the wave energy spectra and fluxes for the Sun by taking the solar gravity (see above), $T_{\rm eff} = 5770$ K, the solar metallicity ( $Z_{\rm m} = 0.02$), the mixing-length parameter $\alpha$ which is assumed to be 2 in all our calculations, and the following three values of the tube magnetic field: $B_{\rm o} / B_{\rm eq} = 0.75$, 0.85 and 0.95. The obtained wave energy spectra are shown in Fig. 1. It is clearly seen that the amount of generated wave energy decreases with increasing magnetic field and that the frequency  $\omega _{\rm max}$ of the maximum of each spectrum is located relatively close to the cutoff frequency  $\Omega _{\rm K}$. Since  $\omega _{\rm max}$ is always less than  $\Omega _{\rm K}$ (see Table 1), the generated transverse tube waves are always propagating waves. The total wave energy fluxes carried by these waves along solar magnetic flux tubes are computed by intergrating the spectra over frequency and the obtained fluxes are given in Table 1. In the following, the fluxes and spectra are used to study the excitation of atmospheric oscillations inside magnetic flux tubes by monochromatic transverse tube waves and a spectrum of these waves, respectively.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4254f1.eps} \end{figure} Figure 1: Transverse wave energy fluxes computed for three different values of the tube magnetic field: $B_{\rm o}$/ $B_{\rm eq} = 0.75$, 0.85 and 0.95 specified at  $\tau _{5000} = 1$.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4254f2.eps} \end{figure} Figure 2: Time evolution of the free atmospheric oscillations inside solar magnetic flux tubes with $B_{\rm o}$/ $B_{\rm eq} = 0.85$. The oscillations are driven by monochromatic transverse tube waves with $\omega = 0.0183$ and  $F_K = 1.4\times 10^{8}$ (erg/cm2s), and the real part of  $v(t,z)/c_{\rm K}$ (see Eq. (14)) is plotted at two different atmospheric heights z=500 km (t = 832 s) and z=2000 km (t = 3326 s).

4.2 Monochromatic waves

To investigate the excitation of the free atmospheric oscillations by monochromatic transverse tube waves, we calculate the initial amplitude $u_{\rm o} = \sqrt {2 F_{\rm K}/ \rho_{\rm o} c_{\rm K}}$, where $F_{\rm K}$ is the total wave energy flux carried by transverse tube waves (see Table 1). Since we consider monochromatic waves, we assume that $\omega = \omega_{\rm max}$, where  $\omega _{\rm max}$ is the maximum frequency of the computed wave energy spectra (see Fig. 1) and is given in Table 1. The time evolution of the wave velocity v(t,z) normalized by $c_{\rm K}$ (see Eq. (14)) is calculated at the atmospheric height z=500 km, which corresponds to t = 832 s, and z=2000 km, which corresponds to t = 3326 s, and plotted in Fig. 2. The presented results clearly show that the amplitude of these oscillations is small when compared to the tube speed $c_{\rm K}$ and quickly decreases with time as t-3/2. A small increase of the amplitude with decreasing tube magnetic field is consistent with changes of $F_{\rm K}$ given in Table 1. Since $F_{\rm K}$ is larger than the total longitudinal wave energy flux $F_{\rm T}$ (see Paper I), the normalized amplitude  $v(t,z)/c_{\rm K}$ of the free atmospheric oscillations caused by transverse tube waves is approximately one order of magnitude larger than the amplitude  $v(t,z) / c_{\rm T}$ for longitudinal tube waves. In addition, the frequency  $\Omega _{\rm K}$ of the oscillations excited by transverse tube waves is approximately two times lower than  $\Omega_{\rm T}$, which is the cutoff frequency for longitudinal tube waves (see Paper I); this can be clearly seen when Fig. 2 of Paper I and Fig. 2 of this paper are compared. According to the results given in Table 1, $\Omega _{\rm K}$ increases by a factor of 1.2 with the increasing magnetic field, which means that the oscillations inside magnetic flux tubes are of higher frequency for stronger magnetic fields.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4254f3.eps} \end{figure} Figure 3: Time evolution of the initial wave velocity  $v_{\rm o} (t)$ normalized by $c_{\rm K}$. These velocity fluctuations represent the spectrum of transverse tube waves shown in Fig. 1 (solid line) at the atmospheric height z=0 km inside solar magnetic flux tubes with $B_{\rm o}$/ $B_{\rm eq} = 0.85$.

4.3 Spectra of waves

The assumption that the total wave energy flux is carried by monochromatic waves is not realistic as the turbulent motions in the solar convection zone generate a full spectrum of waves with different frequencies and amplitudes. Because of the nature of these motions, the amplitudes vary rapidly in time and for a very brief period of time they can be as high as 0.4$c_{\rm K}$ (see Fig. 3). The time evolution of $v_{\rm o}$ shown in Fig. 3 is computed by identifying the frequency  $\omega_{n}$ (see Eq. (15)) of each partial wave with 32 frequency points used in calculations of the wave energy spectra presented in Fig. 1, and by taking $u_{n} = \sqrt{2 F_{n}/ \rho_{\rm o} c_{\rm K}}$, where Fn is the wave energy flux carried by the waves with  $\omega_{n}$. Since all partial waves are propagating ( $\omega_{n} > \Omega_{\rm K}$), we assume that the phase  $\phi_{n} = 0$ is the same for all these waves. The results shown in Fig. 3 represent the spectrum of transverse tube waves propagating along magnetic flux tubes with $B_{\rm o}$/ $B_{\rm eq} = 0.85$ (see Fig. 1). The velocity fluctuations obtained for $B_{\rm o}$/ $B_{\rm eq} = 0.75$ and 0.95 look very similar except that some spikes are even higher for the former and lower for the latter.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4254f4.eps} \end{figure} Figure 4: Time evolution of the free atmospheric oscillations inside solar magnetic flux tubes with $B_{\rm o}$/ $B_{\rm eq} = 0.85$. The oscillations are driven by the spectrum of transverse tube waves shown in Fig. 1 (solid line) and only the real part of $v(t,z)/c_{\rm K}$ is plotted at two different atmospheric heights z=500 km (t = 832 s) and z=2000 km (t = 3326 s).

According to Eq. (16), the spectrum of transverse tube waves propagating along magnetic flux tubes excite the free atmospheric oscillations with the cutoff frequency  $\Omega _{\rm K}$. We calculate the time evolution of these oscillations for all three cases of the tube magnetic field, and plot the real part of Eq. (16) for $B_{\rm o}$/ $B_{\rm eq} = 0.85$ and 0.95 in Figs. 4 and 5, respectively. It is clearly seen that that the oscillations driven by these two spectra decay in time as t-3/2 and that their amplitudes are approximately twice as high as those shown in Fig. 2 for monochromatic waves. By comparing the results shown in Figs. 4 and 5, one finds that the amplitude of these oscillations is very similar for the two considered values of the tube magnetic field. This is rather surprising result as the initial wave energy flux is higher for $B_{\rm o}$/ $B_{\rm eq} = 0.85$ than for 0.95 (see Fig. 1); the difference is caused by the fact that flux tubes with stronger magnetic fields are more difficult to shake (see Musielak & Ulmschneider 2001, for details). As a result of this difference in the wave energy fluxes, the amplitude of the oscillations shown in Fig. 4 should be higher than those presented in Fig. 5.

To explain this apparent discrepancy, we checked the time required for transverse tube waves to reach the atmospheric height z=500 km (z=2000 km) in both cases. We found that this time was 832 s (t = 3326 s) and 690 s (t = 2758 s) for the waves propagating along the tube with $B_{\rm o}$/ $B_{\rm eq} = 0.85$ and 0.95, respectively. Based on Eq. (16), one sees that the longer time reduces the amplitude, however, the shorter time is responsible for its increase; hence, it is a pure coincidence that the amplitudes of the oscillations shown in Figs. 4 and 5 look so similar.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4254f5.eps} \end{figure} Figure 5: The same as Fig. 4 but for $B_{\rm o}$/ $B_{\rm eq} = 0.95$.

The frequency $\Omega _{\rm K}$ of the free atmospheric oscillations shown in Figs. 4 and 5 is different because of different strength of the tube magnetic field (see Table 1). For the oscillations presented in Fig. 4, we have $\Omega_{\rm K} = 0.0129$ s-1, which gives $P_{\rm K} = 2 \pi / \Omega_{\rm K} = 487~{\rm s} \approx 8$ min; however, for the oscillations of Fig. 5, we find $\Omega_{\rm K} = 0.0155$ s-1, which gives  $P_{\rm K} = 405~{\rm s}\approx 7$ min. In both cases, the period of these oscillations is consistent with the observations mentioned in Sect. 1. This agreement has led Kalkofen (1997) and Hasan & Kalkofen (1999) to conclude that the free atmospheric oscillations observed in the chromospheric network are driven by transverse tube waves propagating along solar magnetic flux tubes. Since these waves are continuously generated in the solar convection zone (Musielak & Ulmschneider 2001), in principle they could excite the observed oscillations; however, see our discussion in Sect. 5.

4.4 Random pulses

Finally, we consider a wavetrain of transverse pulses that have random amplitudes and frequencies. The wavetrain is assumed to be finite with the number of pulses determined by the condition t > tN. A new pulse with randomly chosen amplitude and period is introduced after the passed time becomes equal to the period of the previous pulse. For all pulses the condition $\omega_{n} > \Omega_{\rm K}$ must be satisfied, which means only propagating pulses are considered. The source of these pulses can be rapid horizontal motions existing at the top of the solar convection zone and in the solar photosphere (e.g., Muller et al. 1994; Solanki et al. 1996; Steiner et al. 1998). Generation of transverse tube waves and pulses by these large amplitude motions has been studied analytically (Choudhuri et al. 1993a,b; Zhugzhda et al. 1995) and numerically (Huang et al. 1995).

Here, our assumption is that the wavetrain of random pulses described by Eq. (19) is imposed on the tube at z=0 and that these pulses propagate upward along the tube and produce the free atmospheric oscillations. Since the wavetrain is finite only the free oscillations are present (see Eq. (22)) and their time evolution is plotted in Fig. 6. It is seen that each random pulse decays in time as t-3/2 and that their amplitudes are comparable to those shown in Figs. 4 and 5 for the excitation by the spectra of waves. An interesting result is that the oscillations are sustained in the atmosphere for more than 10 000 s, which is the computation time; they would eventually die out because of the finite number of pulses. In order to make these oscillations a permanent atmospheric feature, the pulses must be continuously generated (Sutmann et al. 1998; also Paper I), even so, the maximum amplitude of these oscillations is only 0.01 km s-1 at the atmospheric height z = 2000 km.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4254f6.eps} \end{figure} Figure 6: Time evolution of the free atmospheric oscillations inside solar magnetic flux tubes with $B_{\rm o}$/ $B_{\rm eq} = 0.85$. The oscillations are driven by a wavetrain of transverse pulses with randomly chosen amplitudes and frequencies. The real part of  $v(t,z)/c_{\rm K}$ is plotted at two different atmospheric heights z=500 km (t = 832 s) and z=2000 km (t = 3326 s).

5 Nonlinear wave coupling

Our analytical results show that both transverse tube waves and transverse pulses propagating along a magnetic flux tube freely excite tube oscillations. The frequency of these free oscillations is  $\Omega_{\rm K} = 0.0129$ s-1 and the period is $P_{\rm K} = 2 \pi / \Omega_{\rm K} \approx 8$ min for $B_{\rm o}$/ $B_{\rm eq} = 0.85$. The period becomes longer $P_{\rm K} \approx 10$ min for the weaker magnetic field $B_{\rm o}$/ $B_{\rm eq} = 0.75$ and shorter $P_{\rm K} \approx 7$ min for the stronger field $B_{\rm o}$/ $B_{\rm eq} = 0.95$. This range of periods seems to be in good agreement with the oscillations observed in the chromospheric network (see Sect. 1). However, a fundamental difficulty with the free atmospheric oscillations driven by transverse waves and pulses is that these oscillations give negligible contribution to the Doppler signal and, therefore, they are not visible at disk center (e.g., Kalkofen 1997). According to Hasan & Kalkofen (1999), the oscillations can be detected in the solar chromosphere after transformation of transverse tube waves into longitudinal tube waves. The process responsible for this transformation is the nonlinear mode coupling and these authors assumed that the period of both waves is the same after the transformation. In the following, we discuss this process and the validity of their assumption.

A schematic picture showing how the nonlinear mode coupling works is presented in Fig. 7. It must be noted that in our approach transverse tube waves are generated as linear waves. However, when they propagate in the solar atmosphere their amplitudes increase due to the decrease in density and nonlinear effects (mode coupling to longitudinal tube waves) become important. As a result of these effects, the components of the curvature forces along the verical become large enough to produce compressions inside the tube. For each transverse displacement, there is approximately one compression and one expansion inside the tube. Thus, one full longitudinal tube wave is generated by every half wavelength of a transverse wave, which means that the frequency of the longitudinal tube waves is approximately twice that of the transverse tube waves. This shows that the period of the generated longitudinal tube waves is approximately one half the period of transverse tube waves and that the assumption made by Hasan & Kalkofen (1999) is not correct.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4254f7.eps} \end{figure} Figure 7: A schematic picture showing generation of longitudinal tube waves by nonlinear transverse tube waves. This nonlinear coupling between the modes produces longitudinal tube waves that have frequencies approximately twice as high as transversetube waves.

As shown in Paper I, the period of the longitudinal tube waves is not the main property that determines the period of the resulting free oscillations. Actually, the free atmospheric oscillations excited by the propagating longitudinal tube waves of any frequency inside solar magnetic flux tubes have always a period that is equal to the cutoff period $P_{\rm T} = 2 \pi / \Omega_{\rm T}$. Therefore, the propagation of longitudinal tube waves produced by the nonlinear mode coupling will generate free oscillations with the cutoff frequency  $\Omega_{\rm T}$ but not  $\Omega _{\rm K}$ as suggested by Hasan & Kalkofen (1999). As a result, the period of these oscillations will be near 3 min and will be practically independent of the strength of the tube magnetic field (see Paper I). Thus, we may conclude that both longitudinal tube waves generated in the solar convection zone and longitudinal tube waves produced by the nonlinear mode coupling excite 3-min oscillations inside solar magnetic flux tubes.

Despite the fact that these two different excitation mechanisms produce free atmospheric oscillations inside solar magnetic flux tubes with the same period, their amplitudes are likely to be different. The amplitudes of the oscillations excited by the first mechanism are known and given in Paper I; however, to determine the amplitudes of oscillations produce by the second mechanism, one must know the efficiency of the nonlinear mode coupling (Ulmschneider et al. 1991). Since the energy fluxes carried by transverse tube waves are relatively high (Huang et al. 1995; Musielak & Ulmschneider 2002a), and since the amplitude of these waves quickly increases with height due to the density gradient, the transformation of the waves into longitudinal tube waves must be efficient (e.g., Ulmschneider et al. 2001; Fawzy et al. 2002). If this is the case, then the amplitudes of the free oscillations discussed here must be higher (or even much higher) than those presented in Paper I. To make this comparison more detailed calculations of the efficiency of the nonlinear mode coupling are required, however, calculations of this type are out of the scope of this paper.

It is important to note that our model of exponentially diverging magnetic flux tubes allows us to introduce the global cutoff frequencies ( $\Omega_{\rm T}$, $\Omega_{\rm S}$ and  $\Omega _{\rm K}$) and derive the general analytical solutions for different excitation mechanisms. On the other hand, our model has only limited applications to the Sun. The model is obviously valid for a single magnetic flux tube located inside the supergranulation cells. It may also be applied to appropriate regions of the chromospheric network at the boundary of superganulation cells where enough space is available before the tubes meet neighboring flux tubes. In both cases, the analytical theory presented here predicts only the existence of the 3-min free atmospheric oscillations inside solar magnetic flux tubes. Hence, neither our results nor the results presented by Hasan & Kalkofen (1999) can account for the 7-min oscillations observed in the chromospheric network. Clearly, a different approach is needed to explain the nature and origin of these oscillations.

One possible explanation of the 7-min oscillations has been given by Deubner & Fleck (1990) who suggested that internal gravity waves forming standing waves inside the solar chromospheric cavity may account for the range of periods (see also Lou 1995a,b) and other basic properties of these oscillations. However, Hasan & Kalkofen (1999) argue that this is not sufficient because a theory explaining the observed oscillations must also account for the heating of the chromospheric network. We basically agree with this suggestion and believe that in order to explain the nature and origin of the oscillations in the magnetic network, one must take into account more realistic shapes of the magnetic flux tubes (see, for example, Fawzy et al. 2002) and include the temperature gradient as well. Obviously, for such situations no analytical solutions can be obtained and only the so-called local cutoff frequencies can be derived. The fact that both the period of the free atmospheric oscillations and their time decay are affected by the temperature gradient has been shown by Sutmann & Ulmschneider (1995a) for a magnetic-free atmosphere. Similar studies must be performed for solar magnetic flux tubes discussed here and in Paper I. The results of these studies will be presented elsewhere.

6 Conclusions

Our conclusions about the nature of the oscillations excited by transverse tube waves and pulses can be summarized as follows:

1. The propagation of transverse tube waves and pulses along a single magnetic flux tube leads to the free oscillations of this tube with the cutoff frequency  $\Omega _{\rm K}$. Since this cutoff depends on the strength of the tube magnetic field, the period of these oscillations ranges from 7 to 10 min for the field ranging from $B_{\rm o}$/ $B_{\rm eq} = 0.95$ to 0.75.

2. The free atmospheric oscillations decay in time as t-3/2 if the frequency of driving waves is not equal to the cutoff frequency  $\Omega _{\rm K}$. This time dependence is the same for all considered mechanisms of the excitation of these oscillations.

3. For the continuous excitation, the forced oscillations of the magnetic flux tube are also present. They are different from the free oscillations as they do not decay in time and their frequency is the same as the frequency $\omega$ of the driving waves. However, when  $\omega = \Omega_{\rm K}$ both the free and forced oscillations become identical and they do not decay in time.

4. The amplitude of the free oscillations driven by either transverse tube waves or pulses is relatively small when compared with the characteristic speed $c_{\rm K}$ of these waves. This amplitude is larger for the excitation by a spectrum of waves and random pulses than for monochromatic waves, and it increases when the tube magnetic field is decreased.

5. The free and forced oscillations of solar magnetic flux tubes driven by transverse tube waves and random pulses cannot be directly observed as they do not give a Doppler signal. However, free and forced atmospheric oscillations inside these tubes can be observed if they are excited by longitudinal tube waves generated by transverse tube waves through the process of nonlinear mode coupling (Hasan & Kalkofen 1999). Our results show that the basic properties of these two types of oscillations are different. The main difference is that the former have periods ranging from 7 to 10 min and the latter show always periods near 3 min.

6. The observed 3-min oscillations inside the supergranule cells are consistent both with the free atmospheric oscillations inside magnetic flux tubes and with the free atmospheric oscillations in a nonmagnetic atmosphere outside these tubes. The results presented here and in Paper I show that the former are excited by the propagating longitudinal tube waves generated either by the turbulent motions in the solar convection zone or by transverse tube waves through nonlinear mode coupling. According to our analytical results, in both cases only the 3-min free atmospheric oscillations are produced.

7. Our results cannot explain the 7-min oscillations observed in the chromospheric network. The main reason is that our model does not apply to crowded magnetic flux tubes at the boundary of supergranules. Therefore, to account for these oscillations, one must take into consideration a more realistic structure of flux tubes located in the magnetic network.

Acknowledgements
This work was supported by NSF under grant ATM-0087184 (Z.E.M. and P.U.), by the DFG grant Ul57/25-3, and by NATO under grant CRG-910058 (P.U. and Z.E.M.). Z.E.M. also acknowledges the support of this work by the Alexander von Humboldt Foundation.

References


Copyright ESO 2003