A&A 406, 23-30 (2003)
DOI: 10.1051/0004-6361:20030792
R. Böger1 - W. H. Kegel2,3 - M. Hegmann3
1 - Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112, 21029 Hamburg, Germany
2 -
Institut für theoretische Physik der Universität
Frankfurt am Main, Robert-Mayer Strasse 8-10,
60054 Frankfurt am Main, Germany
3 -
Zentrum für Astronomie und Astrophysik der Technischen Universität
Berlin, Sekr. PN 8-1, Hardenbergstrasse 36,
10623 Berlin, Germany
Received 19 February 2003 / Accepted 20 May 2003
Abstract
The microturbulent approximation of turbulent motions is widely used
in radiative transfer calculations. Mainly motivated by its
simple computational application it is probably in many cases an oversimplified
treatment of the dynamical processes involved.
This aspect is in particular important in the analysis of maser lines,
since the strong amplification of radiation
leads to a sensitive dependence of the radiation field on the overall velocity structure.
To demonstrate the influence of large scale motions on the formation of maser
lines we present
a simple stochastic model which takes velocity correlations into
account. For a quantitative analysis of correlation effects, we generate
in a Monte Carlo simulation individual realizations of a turbulent
velocity field along a line of sight. Depending on the
size of the velocity correlation length we find huge deviations between
the resulting random profiles in respect of line shape, intensity and position
of single spectral components. Finally, we simulate the emission of extended
maser sources. A qualitative comparison with observed masers associated
with star forming regions shows that our model can reproduce the
observed general spectral characteristics. We also investigate briefly,
how the spectra are affected when a systematic velocity field (simulating
expansion) is superposed on the fluctuations. Our results convincingly demonstrate
that hydrodynamical motions are of great importance for
the understanding of cosmic masers.
Key words: masers - radiative transfer - turbulence - line: formation
Maser lines of various molecular species are observed in star forming regions and in the envelopes of evolved late type stars. In both cases it is well known that turbulent motions play an important role in the gas hydrodynamics. Their spectra show large velocity differences (up to tens of km s-1) and are variable on observable time scales. VLBI-observations reveal that maser regions often consist of several isolated sources with different radial velocities (see, e.g., Reid et al. 1980). Due to the Doppler effect, the radiation field depends on the local velocity structure. This coupling to the velocity field does sensitively affect the formation of maser lines since in the unsaturated regime the radiation is exponentially amplified. To the extent that stochastic hydrodynamical velocities are involved, the correlation length, i.e., the length over which the hydrodynamical velocity changes substantially, plays an important role. In the usual microturbulent analysis large scale motions are neglected. As a consequence, each spectral component will generally be attributed to a separate source and could in principle be formed under different physical conditions. The aim of the present investigation is to emphasize the necessity to consider hydrodynamical motions in more detail. We will show how correlated velocity fields affect the line forming process and that omitting this important aspect can lead to erroneous interpretations of observed maser spectra.
Traving and collaborators (Gail et al. 1974;
Traving 1975) developed a theory allowing to account for
correlated turbulent motions![]() in the transfer of line radiation.
In their formalism, the hydrodynamic velocity v along a line of sight is described by a
Markovian process defined by a Gaussian distribution function and an
exponential correlation function. Due to the stochastic modeling of the
velocity field, the intensity also has to be considered as a random
variable. Traving showed that in accord with these assumptions and together
with the usual equation of transfer, a Fokker-Planck equation can be derived,
which describes the probability
in the transfer of line radiation.
In their formalism, the hydrodynamic velocity v along a line of sight is described by a
Markovian process defined by a Gaussian distribution function and an
exponential correlation function. Due to the stochastic modeling of the
velocity field, the intensity also has to be considered as a random
variable. Traving showed that in accord with these assumptions and together
with the usual equation of transfer, a Fokker-Planck equation can be derived,
which describes the probability
![]() of finding at
point s, the intensity
of finding at
point s, the intensity ![]() and the velocity v. Of particular
interest is the expectation value of the intensity
and the velocity v. Of particular
interest is the expectation value of the intensity
![]() since it reflects as a time or spatial average the mean
physical properties of the system. Gail et al. (1975) examined the model of
an unsaturated maser applying the theory described above.
since it reflects as a time or spatial average the mean
physical properties of the system. Gail et al. (1975) examined the model of
an unsaturated maser applying the theory described above.
While this approach gives a first qualitative insight into the effects introduced by a turbulent velocity field, the question arises to which extent the calculated expectation value of the intensity may be directly compared with observed spectra. The answer depends in particular on two issues. The first is the question of how many statistically independent lines of sight contribute to a given observation. This obviously is a function of the spatial resolution. The second point is the question of how many spectra corresponding to individual lines of sight have to be averaged in order to obtain the expectation value with a certain accuracy. As will be shown later, in the case of unsaturated masers this number is very large. In order to investigate these questions we set up a Monte Carlo (MC) simulation scheme to generate individual realizations of the random velocity field. The calculated line profiles reflect the stochastic nature of the turbulent motion along a given line of sight and allow a quantitative analysis of correlation effects.
In the case of an unsaturated maser the occupation numbers of the maser levels
are essentially not affected by the intensity in the maser line.
Consequently, the intensity variation along
any line of sight depends just on the local physical conditions.
In order to focus on the effect of correlated
velocity fields, we assume a plane parallel slab with a homogeneous density
and temperature distribution. Additionally, we take the velocity field to be
quasi-static, presuming that the dynamical time scales are large in comparison
with the duration of individual observations.
The variation of the turbulent velocity along each line of sight is assumed to follow
a Markov process and the
projected velocity v(s) along a line of sight is treated as a random
function of s. The one-point distribution function of v is considered to
be Gaussian with the rms turbulent velocity
![]()
![\begin{displaymath}W\left( v\right) =\frac{1}{\sqrt{2\pi}\sigma_{\rm t}}\cdot\:\exp{\left[
-\frac{v^{2}}{2\sigma_{\rm t}^{2}}\right]} \cdot
\end{displaymath}](/articles/aa/full/2003/28/aah4329/img16.gif) |
(1) |
![\begin{displaymath}f\left( \Delta s\right) =\:\exp\left[ -\frac{\left\vert \Delta s\right\vert
}{l}\right] \cdot
\end{displaymath}](/articles/aa/full/2003/28/aah4329/img20.gif) |
(3) |
![\begin{displaymath}\left\langle \Delta v\right\rangle =-v\left[ 1-\:\exp\left(
-\frac{\left\vert \Delta s\right\vert }{l}\right) \right]
\end{displaymath}](/articles/aa/full/2003/28/aah4329/img22.gif) |
(4) |
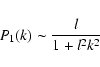 |
(6) |
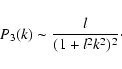 |
(7) |
In accord with Eq. (2) the distribution of the random projected velocities can
be generated in a Monte Carlo procedure (Levshakov et al. 1997):
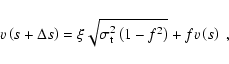 |
(8) |
The line forming process depends sensitively on the ratio
![]() (see, e.g., Levshakov & Kegel 1994).
In the case
(see, e.g., Levshakov & Kegel 1994).
In the case
![]() ,
the line broadening is thermally
dominated and the turbulent velocity correlation is insignificant. Contrary, if
,
the line broadening is thermally
dominated and the turbulent velocity correlation is insignificant. Contrary, if
![]() correlation effects become pronounced. An inappropriately chosen step
size can smear out the correlated structure of a random velocity field. This is
avoided by satisfying the inequality
correlation effects become pronounced. An inappropriately chosen step
size can smear out the correlated structure of a random velocity field. This is
avoided by satisfying the inequality
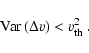 |
(9) |
![\begin{displaymath}\frac{\left\vert\Delta s\right\vert}{l}\le\ln\left[ 1-\left(v_{\rm th}/ \sigma_{\rm t}
\right)^{2}\right]^{-1/2} ~.
\end{displaymath}](/articles/aa/full/2003/28/aah4329/img39.gif) |
(10) |
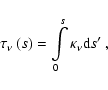 |
(12) |
![\begin{displaymath}\Phi\left( \Delta\nu,v\right)
=\frac{1}{\sqrt{\pi}\Delta\nu_{...
...{\Delta\nu_{\rm D}}-\frac{v}{v_{\rm th}}\right]
^{2}\right\} ,
\end{displaymath}](/articles/aa/full/2003/28/aah4329/img45.gif) |
(14) |
| Greater than | L/l=10 | L/l=25 | L/l=50 |
|
|
69.2% | 37.3% | 15.7% |
|
|
28.0% | 3.5% | 0.13% |
|
|
6.5% | 0.06% | 0.0% |
|
|
0.9% | 0.0% | 0.0% |
Our model calculations mainly depend on three parameters: the optical
thickness of the slab ![]() ,
the turbulent velocity
,
the turbulent velocity
![]() and the
correlation length l. Due to the random nature of the velocity field, the optical
thickness can not be defined uniquely. Therefore, it is characterized by the
optical depth in the line center for vanishing turbulent motions,
and the
correlation length l. Due to the random nature of the velocity field, the optical
thickness can not be defined uniquely. Therefore, it is characterized by the
optical depth in the line center for vanishing turbulent motions,
![]() ,
which is then given by
,
which is then given by
![]() .
.
Figure 2 demonstrates the influence of velocity correlations on the line forming
process. The upper panels show the line profiles for two individual realizations
of the velocity field along a given line of sight calculated with the same statistical parameters (solid curves).
For comparison, also the
expectation values of the intensity are shown (dashed curves). The lower panels give the corresponding
optical depths ![]() .
In our simple model (constant density and constant pumping
efficiency), the latter reflect directly the complex structure
of the underlying velocity field (see Eq. (15)). Due to the exponential
amplification the intensity profiles appear to have a much simpler structure than
the
.
In our simple model (constant density and constant pumping
efficiency), the latter reflect directly the complex structure
of the underlying velocity field (see Eq. (15)). Due to the exponential
amplification the intensity profiles appear to have a much simpler structure than
the ![]() -profiles. This is in particular true if a lower intensity
cut-off is introduced.
Therefore do high intensity spectra often consist of a single line only,
which may exhibit a pronounced line shift.
-profiles. This is in particular true if a lower intensity
cut-off is introduced.
Therefore do high intensity spectra often consist of a single line only,
which may exhibit a pronounced line shift.
As is obvious from Fig. 2 (see also Table 1), the line profiles calculated for
individual realizations of the velocity field can differ substantially from each other
and from the expectation value.
The degree to which an individual realization can deviate from the expectation value can
statistically be described by the convergence behavior of the ensemble average. We
find that in general the mean value approaches the expectation value very slowly. For
the chosen parameter configuration, Fig. 3 shows a sequence of averages
over N realizations. Even the superposition of
![]() individual spectra
is not sufficient to match the spectrum of the intensity expectation value.
For a smaller correlation length or
larger turbulent motions the convergence is improved but still a substantial number
of profiles is required. This finding is contrary to the case of pure absorption. In the
context of quasar absorption lines Levshakov et al. (1997) showed that
the average of about 100 realizations reproduces
the expectation value of the intensity within a one percent error margin.
The radiation of an extended source reflects the average influence of the dynamical motions on the
radiation field. From the above finding it can be concluded that in the case of an
unsaturated maser the expectation value of the intensity will in general not be in good
agreement with the measurements if a finite correlation length is involved. Even if the
problem is solved self-consistently, where, due to saturation effects,
the deviations from the mean intensity will be less pronounced, it can be expected that
the mean intensity will not match the observations. Despite of this conclusion,
the method by Traving is a valuable tool to examine the general influence of the stochastic
parameters which govern the dynamical motions. It allows a very fast calculation of
expectation values and distribution functions (Levshakov et al. 1997).
In this respect, the method is preferable
to a MC simulation which requires the generation of a very large number of realizations and
is thus costly in computer time.
Starting from the same model assumptions, Gail et al. (1975) examined the mean properties of the
radiation field. Their most important finding is that the mean intensity increases with increasing
velocity correlation. This corresponds to our result that with a larger correlation
length the probability of having large peak intensities grows (see Table 1).
In the present paper we want to focus on a different aspect of the problem
for which the MC technique allows a more quantitative comparison of observations and model
calculations.
individual spectra
is not sufficient to match the spectrum of the intensity expectation value.
For a smaller correlation length or
larger turbulent motions the convergence is improved but still a substantial number
of profiles is required. This finding is contrary to the case of pure absorption. In the
context of quasar absorption lines Levshakov et al. (1997) showed that
the average of about 100 realizations reproduces
the expectation value of the intensity within a one percent error margin.
The radiation of an extended source reflects the average influence of the dynamical motions on the
radiation field. From the above finding it can be concluded that in the case of an
unsaturated maser the expectation value of the intensity will in general not be in good
agreement with the measurements if a finite correlation length is involved. Even if the
problem is solved self-consistently, where, due to saturation effects,
the deviations from the mean intensity will be less pronounced, it can be expected that
the mean intensity will not match the observations. Despite of this conclusion,
the method by Traving is a valuable tool to examine the general influence of the stochastic
parameters which govern the dynamical motions. It allows a very fast calculation of
expectation values and distribution functions (Levshakov et al. 1997).
In this respect, the method is preferable
to a MC simulation which requires the generation of a very large number of realizations and
is thus costly in computer time.
Starting from the same model assumptions, Gail et al. (1975) examined the mean properties of the
radiation field. Their most important finding is that the mean intensity increases with increasing
velocity correlation. This corresponds to our result that with a larger correlation
length the probability of having large peak intensities grows (see Table 1).
In the present paper we want to focus on a different aspect of the problem
for which the MC technique allows a more quantitative comparison of observations and model
calculations.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{H4329F3.eps}}
\end{figure}](/articles/aa/full/2003/28/aah4329/Timg59.gif) |
Figure 3: Convergence of the ensemble average of N random profiles (solid line) to its expectation value (dashed line). The parameter configuration is the same as in Fig. 2. |
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[clip]{H4329F4.eps}}
\end{figure}](/articles/aa/full/2003/28/aah4329/Timg64.gif) |
Figure 4:
Simulated spectra of an extended maser region.
Each spectrum is composed of one hundred single realizations. In the upper
ten panels we show the model calculations with a parameter set
of l/L=0.1,
|
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{H4329F6.eps}}
\end{figure}](/articles/aa/full/2003/28/aah4329/Timg67.gif) |
Figure 6:
Expectation values of the intensity calculated for an expanding
plane parallel slap with a constant velocity gradient of
|
Figure 5 shows a selected sample of observed OH and CH3OH maser spectra obtained
by J. Caswell (private communication). A detailed description of most sources can be found
in Caswell (1993, 1998, 2001) together with additional
maser spectra. Our simple model does
clearly not allow a detailed analysis of the observations.
However, it is remarkable that it can reproduce the characteristic structure of the observed
line profiles. Also the velocity scale of our model spectra is in agreement with the
observations, if for example, a typical cloud temperature of 25 K is assumed.
In this case the thermal velocity of the OH and CH3OH molecules is
![]() and
and
![]() ,
respectively.
Due to the higher velocity dispersion,
the spectra in the lower panels of Fig. 4 show a richer structure and span
a larger velocity range than the spectra in the top panels. Of course, also
the amplification of radiation is affected by larger velocity differences along a line of sight.
Therefore, we had to chose for both models very different
opacity parameters to achieve the typical spiky structure of maser profiles.
,
respectively.
Due to the higher velocity dispersion,
the spectra in the lower panels of Fig. 4 show a richer structure and span
a larger velocity range than the spectra in the top panels. Of course, also
the amplification of radiation is affected by larger velocity differences along a line of sight.
Therefore, we had to chose for both models very different
opacity parameters to achieve the typical spiky structure of maser profiles.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{H4329F7.eps}}
\end{figure}](/articles/aa/full/2003/28/aah4329/Timg70.gif) |
Figure 7:
As in Fig. 4 the spectra model the emission of an extended maser region with the parameter configuration:
l/L=0.1,
|
In this context, one may also ask how an additional systematic velocity field
influences the line formation. For this purpose we considered an expanding
plane parallel slab with a constant systematic velocity gradient superposed on the stochastic
velocity field. The general effect of
this modification of our model can be viewed in Fig. 6 where the expectation
value of the intensity for various values of the expansion velocity is shown (solid lines).
As expected, this additional velocity component leads on average to a
weakening of the radiated emission and to a shift of the velocity distribution function.
Additionally, a slight broadening of the profile of the intensity expectation value is seen. Its
width gives directly an estimation of the velocity range over which individual random
spectra will be distributed.
The shape of individual line profiles is very sensitive to changes of the velocity
field. In Fig. 7 we model again the radiation of a maser region by a superposition of
![]() lines of sight. The turbulent velocity field is in all cases the same and only
the strength of the linear expansion differs. From this example it is obvious
that even small outflow velocities can significantly change the appearance of the resulting
spectra. The tendency that with increasing systematic motions the emission
is reduced is also clearly seen. But the gradients of the systematic and the turbulent
velocity field can also partly compensate each other, allowing a strong amplification of
radiation along particular lines of sight. This behavior is seen in the sequence
lines of sight. The turbulent velocity field is in all cases the same and only
the strength of the linear expansion differs. From this example it is obvious
that even small outflow velocities can significantly change the appearance of the resulting
spectra. The tendency that with increasing systematic motions the emission
is reduced is also clearly seen. But the gradients of the systematic and the turbulent
velocity field can also partly compensate each other, allowing a strong amplification of
radiation along particular lines of sight. This behavior is seen in the sequence
![]() and in the case
and in the case
![]() .
.
It is also instructive to simulate the spatial intensity distribution of composite spectra.
As described before the
emerging radiation from our model cloud is approximated by the superposition
of
![]() independent lines
of sight corresponding to individual realizations of the velocity field.
The general characteristics of the spatial intensity map of the cloud's surface can be simulated
by distributing the maximum intensity found in each contributing spectrum randomly on a square grid
of
independent lines
of sight corresponding to individual realizations of the velocity field.
The general characteristics of the spatial intensity map of the cloud's surface can be simulated
by distributing the maximum intensity found in each contributing spectrum randomly on a square grid
of
![]() cells. In Fig. 8 we consider as an example the spectrum marked with an
asterisk in Fig. 4. The black circles indicate
maximum intensities greater than ten times the expectation value in the line center.
Their number corresponds to the number of distinct spectral components. The grey and white
circles show maximum intensities in the range between
cells. In Fig. 8 we consider as an example the spectrum marked with an
asterisk in Fig. 4. The black circles indicate
maximum intensities greater than ten times the expectation value in the line center.
Their number corresponds to the number of distinct spectral components. The grey and white
circles show maximum intensities in the range between
![]() and
and
![]() respectively.
The maximum intensity in the blank boxes is below one tenth of the expectation value of
the intensity in the line center. Due to the underlying stochastic velocity field,
large spatial intensity
variations are seen.
Similar to observed high resolution intensity maps the maser region consists
of a few strong sources at
different radial velocities (see, e.g., Reid et al. 1980), while
the radiation from most of the region is inconspicuous.
respectively.
The maximum intensity in the blank boxes is below one tenth of the expectation value of
the intensity in the line center. Due to the underlying stochastic velocity field,
large spatial intensity
variations are seen.
Similar to observed high resolution intensity maps the maser region consists
of a few strong sources at
different radial velocities (see, e.g., Reid et al. 1980), while
the radiation from most of the region is inconspicuous.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{H4329F8.eps}}
\end{figure}](/articles/aa/full/2003/28/aah4329/Timg75.gif) |
Figure 8:
Spatial intensity distribution of the spectrum in Fig. 4
marked with an asterisk. Black circles indicate a maximum intensity
of a single realization greater than ten times the expectation
value in the line center. Grey and white
circles show maximum intensities in the range between
|
In the previous sections we have investigated the influence of a turbulent velocity field with finite correlation length on the appearance of a cosmic maser source. For this, we used a very simple stochastic model in which the only spatially varying quantity is the hydrodynamical velocity, while all other parameters, in particular the density and the pump efficiency are held constant. With this simple model, we could to a surprisingly high degree reproduce the observed characteristics of cosmic masers, in particular those related to star forming regions. Our results are a strong indication that the details of the hydrodynamic velocity field inside a maser region are of great importance for the interpretation of the observed properties of the source. Of course, reality is considerably more complex than our simple model. It is very likely that in star forming regions not only the velocity is a fluctuating quantity, but also the density and other physical parameters determining the pump efficiency show strong spatial variations. However, our results convincingly show that the observation of a maser spot, by itself does not necessarily imply that the physical conditions at the location of the spot are peculiar. The spot may as well be the result of the details of the velocity distribution along the line of sight.
In view of the simplicity of our model, we have made no attempt to compare results
in more detail with observational results of particular maser regions. Such attempts, however,
have been performed by other authors investigating effects of turbulent motions on
maser spectra. The approach closest to ours is that of Sobolev et al. (1998).
They consider also a slab which is homogeneous except for the velocity field.
The latter is characterized by its statistical properties. From these, individual
realizations of the velocity field are constructed which then are used to calculate the
optical depth and the emitted spectrum. Their approach differs from ours in the assumptions about
the velocity field and in the numerical procedure. For the velocity field they assume a
more general power spectrum
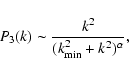 |
(16) |
A very different approach is followed by Gwinn (1994a,b). He tries to solve the inverse problem, i.e. he attempts to derive the characteristics of the velocity field directly from the very detailed observations available for the H2O maser region in W49N. The observations are interpreted by a model in which a strong stellar wind strikes ambient material and the arising shocks provide the excitation energy for the masers. More than 250 maser features were identified. Gwinn measures the distribution of the individual maser spots in coordinate and velocity space. From the derived power law correlation functions he concludes that the velocity field in the maser region is turbulent. This interpretation of the observations makes the (implicit) assumption that the velocities of the individual maser spots reflect directly the velocity field in the maser region. This assumption is appropriate if one considers the maser spots as physical entities like clumps. If one considers models like ours or that of Sobolev et al. (1998), in which the maser spots are solely caused by the correlations in the velocity field, the situation is more complex (see Fig. 2).
A similar statistical analysis of high quality observational data for the H2O masers in the star forming regions Sgr B2(M), W49N, W51(MAIN), W51N, and W3(OH) has been performed by Strelnitski et al. (2002). They find that the two-dimensional distribution of maser spots shows a fractal structure and that the two-point velocity structure functions can be approximated by power laws with exponents close to Kolmogorov's values. From these findings they conclude that the velocity field in these maser regions is highly turbulent.
Acknowledgements
We thank Dr. James Caswell for providing the observed maser spectra shown in Fig. 5 and for many interesting discussions. We also acknowledge constructive comments of the referee Dr. C. R. Gwinn, as well as discussions with Dr. B. Deiss and C. Hengel on the different types of correlation functions and power spectra.
This research has been partly supported by the BMBF/DLR under Grant No. 50 OR 0203.