A&A 406, 345-356 (2003)
DOI: 10.1051/0004-6361:20030676
Transition region, coronal heating and the fast solar wind
Xing Li
Department of Physics, University of Wales, Aberystwyth, SY23 3BZ, UK
Received 31 October 2002 / Accepted 28 April 2003
Abstract
It is assumed that magnetic flux tubes are strongly
concentrated at the boundaries of supergranule convection cells. A
power law spectrum of high frequency Alfvén waves with a
spectral index -1 originating from the sun is assumed to supply
all the energy needed to energize the plasma flowing in such
magnetic flux tubes. At the high frequency end, the waves are
eroded by ions due to ion cyclotron resonance. The magnetic flux
concentration is essential since it allows a sufficiently strong
energy flux to be carried by high frequency ion cyclotron waves
and these waves can be readily released at the coronal base by
cyclotron resonance. The main results are: 1. The waves are
capable of creating a steep transition region, a hot corona and a
fast solar wind if both the wave frequency is high enough and the
magnetic flux concentration is sufficiently strong in the
boundaries of the supergranule convection zone. 2. By primarily
heating alpha particles only, it is possible to produce a steep
transition region, a hot corona and a fast solar wind. Coulomb
coupling plays a key role in transferring the thermal energy of
alpha particles to protons and electrons at the corona base. The
electron thermal conduction then does the remaining job to create
a sharp transition region. 3. Plasma species (even ions) may
already partially lose thermal equilibrium in the transition
region, and minor ions may already be faster than protons at the
very base of the corona. 4. The model predicts high temperature
alpha particles (
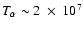 K) and low proton
temperatures (
K) and low proton
temperatures (
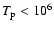 K) between 2 and 4 solar radii,
suggesting that hydrogen Lyman lines observed by UVCS above
coronal holes may be primarily broadened by Alfvén waves in this
range.
K) between 2 and 4 solar radii,
suggesting that hydrogen Lyman lines observed by UVCS above
coronal holes may be primarily broadened by Alfvén waves in this
range.
Key words: Sun: corona -
Sun: solar wind - Sun: transition region
It has been well known for several decades that the solar wind is
the expansion of the hot corona along open magnetic field flux
tubes. However, the exact mechanisms responsible for the creation
of a hot corona and the acceleration of the fast solar wind
continue to be an unresolved issue (Axford et al. 1999; Marsch
1999). Since the fast solar wind streams and the corona are
connected, there has been a growing awareness that the two
problems should be treated in a self-consistent way. It is also
natural to seek a single theory to account for the coronal heating
and the acceleration of the fast solar wind along open magnetic
field fluxes. However, the Sun and the inner corona are far away,
the environment near the Sun is harsh for the survival of space
probes, so in situ measurements of the plasma parameters in the
near Sun region are still not available. Without in situ
measurements, it is difficult to tell what is responsible for the
coronal heating and the acceleration of the fast solar wind.
However, as the fast solar wind cruises into interplanetary space,
manmade satellites have been able to detect the properties of the
fast (and slow) solar wind streams over the past few decades.
These direct measurements have shown that Alfvén waves are
ubiquitous in fast solar wind streams (e.g., Belcher & Davis
1971; Smith et al. 1995). They provide an attractive mechanism for
the solar wind heating and acceleration if their high frequency
counterparts, whose energy can be directly absorbed by the solar
wind plasmas, exist in the inner corona.
However, power spectra of magnetic field fluctuations in the solar
wind, most likely of Alfvénic nature, are typically of the form
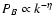 ,
where k is the wavenumber and
,
where k is the wavenumber and 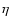 the spectral index. Since observations yield
the spectral index. Since observations yield
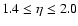 (Bavassano et al. 1982), most of the power in the Alfvénic
fluctuations is in the frequency range below the ion cyclotron
frequency. Hence no substantial influence of these waves on ions
can be expected (see Isenberg & Hollweg 1983; Marsch et al.
1982). This difficulty can be overcome if the Sun launches waves
in the ion cyclotron resonance range leading to the heating and
acceleration of the solar wind (e.g., Axford & McKenzie 1995;
McKenzie et al. 1995, 1997; Tu & Marsch 1997), or if there
exists some mechanism which replenishes the resonant wave power as
soon as it is absorbed by the particles.
(Bavassano et al. 1982), most of the power in the Alfvénic
fluctuations is in the frequency range below the ion cyclotron
frequency. Hence no substantial influence of these waves on ions
can be expected (see Isenberg & Hollweg 1983; Marsch et al.
1982). This difficulty can be overcome if the Sun launches waves
in the ion cyclotron resonance range leading to the heating and
acceleration of the solar wind (e.g., Axford & McKenzie 1995;
McKenzie et al. 1995, 1997; Tu & Marsch 1997), or if there
exists some mechanism which replenishes the resonant wave power as
soon as it is absorbed by the particles.
To tap into the energy available in Alfvénic fluctuations,
Hollweg (1986) assumed that a nonlinear cascade process, namely,
the Kolmogorov dissipation of Alfvénic turbulence, transports
energy from the low-frequency waves to the ion cyclotron resonant
range, where it is picked up by the plasma through the cyclotron
resonance. Hollweg & Johnson (1988) extended this idea to a
two-fluid solar wind model. Their results yielded the right
qualitative features: a steep temperature rise in the transition
region to over 106 K in the corona and acceleration to
supersonic speeds. These studies showed that the Kolmogorov
dissipation rate is not capable of creating a transition region, a
hot corona and a fast solar wind simultaneously, even though it
seems that the mechanism is able to produce a fast solar wind
(Isenberg 1990; Li et al. 1999).
Recent remote sensing observations from the Ultraviolet
Coronagraph Spectrometer (UVCS) and Solar Ultraviolet Measurements
of Emitted Radiation (SUMER) on board Solar and Heliospheric
Observatory (SOHO) have enhanced our interests in the ion
cyclotron resonance for coronal heating and solar wind
acceleration. SUMER spectral line observations at the base of the
corona in a southern coronal hole indicate that the temperature of
minor ions decreases with increasing mass per charge (Tu et al.
1998). The temperature difference of various ions is more
pronounced in the inner corona. UVCS observations reveal that ions
not only have greater than mass-proportional temperatures in the
inner corona, they are much hotter than electrons and are highly
anisotropic as well (Kohl et al. 1998; Li et al. 1999; Cranmer et al. 1999). By recognizing the importance of the pumping by the
second C II line in the interpretation of the UVCS observations,
Li et al. (1998) concluded that the outflow speed of O+5 is
about 400
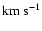 at 3 RS, already faster than
protons, and these oxygen ions also have a large temperature
anisotropy at the same distance. These recent advances strongly
indicate that ion cyclotron resonance may indeed play an important
role in the coronal heating (at least along open field lines),
thus enhancing the interest in ion cyclotron resonance. Various
models have been published to explain observations and make
predictions using ion cyclotron resonance (see a thorough review
by Hollweg & Isenberg 2002 and the references).
at 3 RS, already faster than
protons, and these oxygen ions also have a large temperature
anisotropy at the same distance. These recent advances strongly
indicate that ion cyclotron resonance may indeed play an important
role in the coronal heating (at least along open field lines),
thus enhancing the interest in ion cyclotron resonance. Various
models have been published to explain observations and make
predictions using ion cyclotron resonance (see a thorough review
by Hollweg & Isenberg 2002 and the references).
One similar approach to tackle the lack of wave power at high
frequencies in the solar wind is to include the non-linear
interaction between outward propagating and inward propagating
Alfvén waves. The non-linear interaction can result in a strong
cascade. The idea was introduced by Tu et al. (1984). The cascade
is able to explain the magnetic field spectrum evolution and to
account for the proton heating beyond 10 solar radii (Tu 1987,
1988). In a series of papers, Hu and his co-authors applied this
idea to the inner corona, and found that the cascade indeed is
able to account for the heating and acceleration of fast solar
wind (including minor ions) originating in coronal holes (Hu et al. 1999, 2000; Hu & Habbal 1999). In these studies, a hot corona
was treated as a boundary condition, the creation of a steep
transition region and a hot corona were not considered. Although
these turbulence cascade models are promising, it is still not
clear what is the source of the necessary inward propagating waves
and whether these inward propagating waves exist at all in the
inner corona. It is also not clear if the non-linearity of waves
in the corona is strong enough to produce cascades since wave
amplitudes are small.
High frequency Alfvén waves have also been suggested (Axford &
McKenzie 1995), and been adopted to produce a steep transition
region and a hot corona (Marsh & Tu 1997a,b; Hackenberg et al.
2000), or to accelerate the fast solar wind (Tu & Marsch 1997) by
adopting a two fluid approach. Kinetic models have also been
developed by assuming a relatively hot corona boundary (Vocks &
Marsch 2001, 2002). It has been found that plasma species may
already lose thermal equilibrium at the very base of the corona or
the top of transition region. The two fluid models developed by
Hackenberg et al. (2000) can only reach 2 solar radii. The
kinetic models developed by Vocks & Marsch (2002) become
numerically unstable at a few solar radii before reaching cruising
speed and the preferential acceleration of minor ions is not
accounted for. More recently, the above-mentioned two fluid
transition region models were extended to a three fluid approach:
the most abundant minor ions alpha particles were included in
model calculations (Li 2002). It was shown that by heating alpha
particles alone, a transition region, and a hot corona can be
formed due to Coulomb coupling between alpha particles and
protons, Coulomb coupling between protons and electrons, and the
electron heat flux. Considering the strong evidence of ion
cyclotron heating in the extended corona above polar coronal holes
as mentioned above, one would naturally ask: can these high
frequency Alfvén waves produce a self-consistent solution of a
transition region, a hot corona and a fast wind if alpha particles
are considered?
The goal of this paper is to develop a single coherent solution of
a steep transition region, a hot corona and a fast solar wind
stream using one single mechanism and including alpha particles.
In this paper, it is assumed that an outward propagating power law
spectrum of high frequency Alfvén waves (reaching ion cyclotron
frequency) already exists below the transition region (Axford &
McKenzie 1995; Tu & Marsch 1997). Physically, there are no
"boundaries" between the corona and the solar wind. This one
dimensional fluid model includes electrons, protons and alpha
particles. A power law spectrum of Alfvén waves is assumed to
supply all the energy needed to heat the corona and accelerate the
solar wind. It is found that such a mechanism is capable of
creating a steep transition region, a hot corona and a fast solar
wind. Readers may also refer to the work by Hansteen & Leer
(1995), Hansteen et al. (1997) and Lie-Svendsen et al. (2002) who
also considered chromosphere and ionization in their models. In
those models, different heating mechanisms were used. In
particular, Hansteen et al. (1997) have also included alpha
particles in their models.
Standard three-fluid plasma transport equations for electrons,
protons and alpha particles are considered, including heat
conduction and radiation losses. We consider an isotropic,
charge-neutral plasma. The one-dimensional model studied here is
the same as those in Li et al. (1997) and Hu & Habbal (1999), and
the governing equations will not be repeated.
It is assumed that the magnetic flux tubes are strongly
concentrated at the boundaries of the supergranule convection
cells (Gabriel 1976; Marsch & Tu 1997; Hackenberg et al. 2000; Li
2002). The plasma moves along the open magnetic field lines,
and eventually builds up the solar wind. The flow tube cross section area is
a(r)=r2 f(r). We
assume that the magnetic flux tubes in this paper have a two-step
expansion:
and
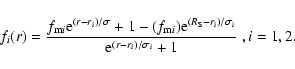 |
(2) |
Here
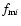 ,
ri, and
,
ri, and 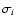 are constants.
Parameters will be chosen such that f1(r) roughly represents a
small scale expansion above the transition region, and the
f2(r) represents the flux tube expansion beyond the solar disk.
The first expansion reaches its full expansion at a height about
15 000 km, similar to the expansion factor used in the transition
region and coronal heating models of Marsch & Tu (1997a) and Li
(2002). The expansion function is taken from Kopp & Holzer (1976)
for simplicity.
are constants.
Parameters will be chosen such that f1(r) roughly represents a
small scale expansion above the transition region, and the
f2(r) represents the flux tube expansion beyond the solar disk.
The first expansion reaches its full expansion at a height about
15 000 km, similar to the expansion factor used in the transition
region and coronal heating models of Marsch & Tu (1997a) and Li
(2002). The expansion function is taken from Kopp & Holzer (1976)
for simplicity.
In this study the Coulomb logarithm
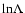 is taken to be 21,
it is assumed that plasmas in the transition region are collision dominated and
classical thermal conduction parallel to the magnetic field can be
used for the electrons, protons and alpha particles. However, the
heat flux of protons rapidly becomes negligible with increasing
heliocentric distances reflecting the collision-less nature of the
proton gas (Li 1999; Olsen & Leer 1999). To simulate this effect,
we take
is taken to be 21,
it is assumed that plasmas in the transition region are collision dominated and
classical thermal conduction parallel to the magnetic field can be
used for the electrons, protons and alpha particles. However, the
heat flux of protons rapidly becomes negligible with increasing
heliocentric distances reflecting the collision-less nature of the
proton gas (Li 1999; Olsen & Leer 1999). To simulate this effect,
we take
![\begin{displaymath}\begin{array}{l}
\kappa_{\rm e}=7.8\times10^{-7}T^{5/2}_{\rm ...
...{\rm S} \over \xi R_{\rm S}} \right)^2 \right]\cdot
\end{array}\end{displaymath}](/articles/aa/full/2003/28/aah4077/img20.gif) |
(3) |
The parameter 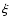 is taken to be 0.22 (however, the model
results are found not sensitive to
is taken to be 0.22 (however, the model
results are found not sensitive to 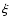 when it changes in the
range
when it changes in the
range
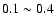 ). When the exponential factors in the above
equations are dropped, they become the collision dominated heat
flux conductivities (Spitzer 1962; Braginskii 1965).
). When the exponential factors in the above
equations are dropped, they become the collision dominated heat
flux conductivities (Spitzer 1962; Braginskii 1965).
The radiative energy loss in the electron energy equation is
assumed to have the form parameterized by Rosner et al. (1978) for
an optically thin medium. It strongly depends on the density of
electrons.
When high frequency Alfvén waves propagate along open coronal
magnetic field lines, ion cyclotron resonance may produce an upper
limit 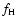 on the frequency of Alfvén waves by a sweeping
mechanism (Marsch & Tu 1997). Following Tu (1987) and Hu & Habbal
(1999),
on the frequency of Alfvén waves by a sweeping
mechanism (Marsch & Tu 1997). Following Tu (1987) and Hu & Habbal
(1999), 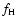 is taken as
is taken as
 |
(4) |
where
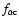 is the gyro-frequency of alpha particles.
The phase speed of an Alfvén wave is
is the gyro-frequency of alpha particles.
The phase speed of an Alfvén wave is
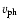 .
The
.
The
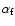 is a constant less than unity, taken to be 0.7 in
this study. This constant was taken to be
is a constant less than unity, taken to be 0.7 in
this study. This constant was taken to be 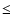 0.2 in previous
studies (Tu & Marsch 1997; Hu & Habbal 1999; Li 2002). At such a
low frequency, alpha particles are not in resonance with ion
cyclotron waves in a low beta plasma such as the one considered
here. When
0.2 in previous
studies (Tu & Marsch 1997; Hu & Habbal 1999; Li 2002). At such a
low frequency, alpha particles are not in resonance with ion
cyclotron waves in a low beta plasma such as the one considered
here. When
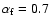 ,
ion cyclotron waves are already
weakly dispersive. To avoid the complexity involved in the wave
spectral evolution equation due to the wave dispersion (Eqs. (19), (20) and (21), Hu & Habbal 1999), non-dispersive approximation is
assumed.
,
ion cyclotron waves are already
weakly dispersive. To avoid the complexity involved in the wave
spectral evolution equation due to the wave dispersion (Eqs. (19), (20) and (21), Hu & Habbal 1999), non-dispersive approximation is
assumed.
The wave power spectrum density, P(f,r), is related to the
magnetic field variance
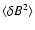 and the
Alfvén wave pressure
and the
Alfvén wave pressure 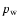 by
by
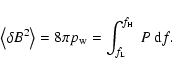 |
(5) |
It is assumed that the Alfvén waves originating below the
transition region have a minimum frequency 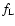 and a
maximum frequency
and a
maximum frequency 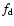 .
If
.
If
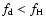 ,
these
Alfvén waves do not resonate with ions, and no wave heating will
result. In such a case,
,
these
Alfvén waves do not resonate with ions, and no wave heating will
result. In such a case, 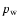 will be related to the wave
power spectrum P(f,r) as
will be related to the wave
power spectrum P(f,r) as
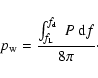 |
(6) |
Following Marsch & Tu (1997a), it is also assumed that
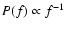 ,
which was suggested by observations in the
ecliptic near 0.3 AU (Bavassano et al. 1982; Marsch & Tu 1990)
and over the poles (Horbury et al. 1995).
,
which was suggested by observations in the
ecliptic near 0.3 AU (Bavassano et al. 1982; Marsch & Tu 1990)
and over the poles (Horbury et al. 1995).
The treatment of the wave spectral evolution closely follows Hu &
Habbal (1999), however non-linear cascade is ignored in this
study. The plasma in a magnetic flux tube is only heated by a
sweeping mechanism (Marsch & Tu 1997a). The total dissipation
rate from this mechanism is divided between the acceleration and
heating for different ion species determined by the microphysics
of the resonant interaction. For a Maxwellian distribution of a
thermally isotropic plasma interacting with a spectrum of parallel
left-hand-polarized ion cyclotron waves, the resonant acceleration
and heating rate of species i are given by Dusenberg & Hollweg
(1981), Marsch et al. (1982) and also Hu & Habbal (1999). In the
evaluation of the integrals involved in the quasi-linear terms,
the wave power spectrum and the dispersion relation in the
dissipation range must be known. Due to the strong magnetic field
in the transition region, the plasma beta value is small. Hence
cold plasma approximation for the dispersion of these waves can be
adopted. Since ion cyclotron resonance is very efficient in
dissipating wave power in small scales,
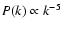 is
assumed in this study. It will be shown, in the transition region
and near Sun region, that the outflow velocity difference between
alpha particles and protons is small compared with Alfvén speed,
as cold plasma dispersion effectively prohibits cyclotron
resonance between waves and protons.
is
assumed in this study. It will be shown, in the transition region
and near Sun region, that the outflow velocity difference between
alpha particles and protons is small compared with Alfvén speed,
as cold plasma dispersion effectively prohibits cyclotron
resonance between waves and protons.
The time-dependent equations of the three-fluid plasma system are
numerically integrated with variable step sizes in space and time
using a fully implicit scheme described by Hu et al. (1997) and Li
et al. (1997). Model calculations start from a point in the lower
transition region where the temperature is
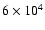 K and
extend to 50
K and
extend to 50  .
The radial step dr gradually increases
from 35 m at the lower boundary, to about
.
The radial step dr gradually increases
from 35 m at the lower boundary, to about
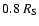 at the
top of the computational domain, and 1100 grid points are used in
calculations. The maximum error in any of the conserved quantities
is less than 1% once a steady state is reached.
at the
top of the computational domain, and 1100 grid points are used in
calculations. The maximum error in any of the conserved quantities
is less than 1% once a steady state is reached.
In this section, model calculations are presented. Calculations
start at
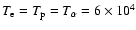 K. The
starting temperature is chosen so that both hydrogen and helium
are
almost fully ionized, and complications involved with ionization
can be avoided (Hansteen et al. 1997). The corresponding electron
density at the boundary is
K. The
starting temperature is chosen so that both hydrogen and helium
are
almost fully ionized, and complications involved with ionization
can be avoided (Hansteen et al. 1997). The corresponding electron
density at the boundary is
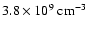 .
The
adopted electron thermal pressure is
.
The
adopted electron thermal pressure is
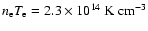 .
This pressure is typical in
coronal holes according to (Warren & Hassler 1998). Warren &
Hassler (1998) found that thermal pressure is roughly a constant
(log
.
This pressure is typical in
coronal holes according to (Warren & Hassler 1998). Warren &
Hassler (1998) found that thermal pressure is roughly a constant
(log
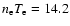 )
in the transition region when the
electron temperature varies from
)
in the transition region when the
electron temperature varies from
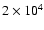 to 106 K. Our
computations end at 52.5 solar radii.
At 52.5 solar radii, the
fast solar wind should be almost fully developed, and beyond 10 solar radii, the cascading effect may not be ignored (Tu 1987).
Three models will be presented in this study, some common
parameters of these models at the base of the open magnetic flux
tube and the flux tube geometry are listed in Table 1.
to 106 K. Our
computations end at 52.5 solar radii.
At 52.5 solar radii, the
fast solar wind should be almost fully developed, and beyond 10 solar radii, the cascading effect may not be ignored (Tu 1987).
Three models will be presented in this study, some common
parameters of these models at the base of the open magnetic flux
tube and the flux tube geometry are listed in Table 1.
Table 1:
Conditions at the base of an open magnetic flux and flux geometry.
 |
We first present model calculations with strong magnetic flux
concentration in the supergranule convection zone boundaries.
Parameters at the lower computation boundary used in this study
are listed in Table 1. The flux tube geometry parameters are as
follows:
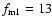 is the maximum expansion factor of the
cross-section of a flux tube in the transition region,
is the maximum expansion factor of the
cross-section of a flux tube in the transition region,
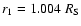 is the heliocentric distance at which the
major expansion takes place. The parameter
is the heliocentric distance at which the
major expansion takes place. The parameter
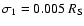 represents the length over which the expansion occurs. This
first super-radial expansion is complete by about 15 000 km. The
parameters for the second super-radial expansion are:
represents the length over which the expansion occurs. This
first super-radial expansion is complete by about 15 000 km. The
parameters for the second super-radial expansion are:
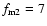 ,
,
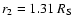 and
and
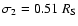 .
This
expansion is complete at about 3
.
This
expansion is complete at about 3
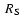 ,
above 3
,
above 3
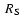 ,
the solar wind is almost radial.
,
the solar wind is almost radial.
The magnetic field at the bottom of the funnel is 123.5 G. This
means that we assume the coronal funnels considered here may
originate from deep in the photosphere (Dowdy et al. 1986). The
low-frequency end of the wave spectrum is fixed at
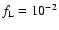 Hz. The wavelength of the waves below this frequency
is very large compared to the scale height in the transition
region and corona. Hence those waves are ignored. The
high-frequency end of the wave spectrum
Hz. The wavelength of the waves below this frequency
is very large compared to the scale height in the transition
region and corona. Hence those waves are ignored. The
high-frequency end of the wave spectrum 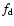 will be
treated as a free parameter. This parameter determines where ion
cyclotron resonance occurs in a flux tube, as can be seen from
Fig. 1.
will be
treated as a free parameter. This parameter determines where ion
cyclotron resonance occurs in a flux tube, as can be seen from
Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{H4077F1.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg54.gif) |
Figure 1:
Gyro-frequency of alpha particles in a flux tube, the
curve for 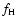 (dashed line) is taken from model 1 in Fig. 2.
(dashed line) is taken from model 1 in Fig. 2. |
Figure 1 shows the gyro-frequency of alpha particles
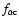 and
and 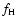 as a function of height h, which is defined
by h=r-r0, and where r0 is the heliospheric distance at the
lower boundary (assumed to be
as a function of height h, which is defined
by h=r-r0, and where r0 is the heliospheric distance at the
lower boundary (assumed to be 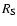 ). Below 105 km,
flow velocities are much smaller than the Alfvén speed and
). Below 105 km,
flow velocities are much smaller than the Alfvén speed and
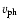 is nearly identical to
is nearly identical to 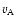 .
As a result,
.
As a result,
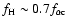 ,
,
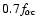 is
roughly the frequency at which cyclotron resonance transfers the
wave energy to alpha particles. However,
is
roughly the frequency at which cyclotron resonance transfers the
wave energy to alpha particles. However, 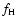 can be
Doppler shifted and become larger than
can be
Doppler shifted and become larger than
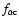 at
larger distances. If
at
larger distances. If
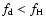 ,
no wave heating will
occur but the waves can still transfer momentum to the plasma (via
wave pressure gradient). The abundance of alpha particles is
chosen at 6%. This abundance is slightly higher than its in situ
measured value of about 5% in fast solar wind streams, but lower
than the helium abundance at the photosphere. Previous solar wind
models showed that this abundance at the coronal base can often
lead to observed helium abundance in interplanetary space (Li et al. 1997; Hu & Habbal 1999).
,
no wave heating will
occur but the waves can still transfer momentum to the plasma (via
wave pressure gradient). The abundance of alpha particles is
chosen at 6%. This abundance is slightly higher than its in situ
measured value of about 5% in fast solar wind streams, but lower
than the helium abundance at the photosphere. Previous solar wind
models showed that this abundance at the coronal base can often
lead to observed helium abundance in interplanetary space (Li et al. 1997; Hu & Habbal 1999).
![\begin{figure}
\par\includegraphics[width=16cm,clip]{H4077F2.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg59.gif) |
Figure 2:
A coronal heating and fast solar wind model in which
the plasma is heated by ion cyclotron waves, Model 1. a)
Speed of protons (thin solid line) and alpha particles (thick solid line).
b) Temperature of
electrons (dotted line), protons (thin solid line) and alpha
particles (thick solid line). The dashed-dotted line is the proton
effective temperature calculated from model 1. The narrow and wide
vertical bars represent the observed proton effective temperatures
from UVCS observations reported by Esser et al. (1999) and Kohl et al.
(1998), respectively. c) Density of protons (thin solid line)
and alpha particles (thick solid line). d) Heating rates of
protons (thin solid line) and alpha particles (thick solid line).
Here
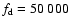 Hz. Hz. |
A steady state solution for the model calculations is shown in
Fig. 2 (model 1). 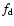 is taken to be 50 000 Hz, so the wave
heating starts at h=300 km (see Figs. 1 and 3). Ion cyclotron
waves indeed produce a very rapid temperature increase, a hot
corona and a fast solar wind: the speed of protons and alphas is
767 km s-1 and 826 km s-1 at 52.5 solar radii, respectively. The
particle flux of protons is
is taken to be 50 000 Hz, so the wave
heating starts at h=300 km (see Figs. 1 and 3). Ion cyclotron
waves indeed produce a very rapid temperature increase, a hot
corona and a fast solar wind: the speed of protons and alphas is
767 km s-1 and 826 km s-1 at 52.5 solar radii, respectively. The
particle flux of protons is
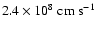 ,
scaled to 215 solar radii (1 AU), a typical observed value in the
fast solar wind at 1 AU (Phillips et al. 1995). The initial
heating of alpha particles is extremely strong, the temperature of
alpha particles already reaches
,
scaled to 215 solar radii (1 AU), a typical observed value in the
fast solar wind at 1 AU (Phillips et al. 1995). The initial
heating of alpha particles is extremely strong, the temperature of
alpha particles already reaches
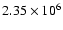 K at the very
bottom (which is shown more clearly in Fig. 3). The heating rate
of alpha particles
K at the very
bottom (which is shown more clearly in Fig. 3). The heating rate
of alpha particles 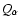 declines by three orders of
magnitude in a narrow region. Roughly speaking, only alpha
particles are heated below 2
declines by three orders of
magnitude in a narrow region. Roughly speaking, only alpha
particles are heated below 2
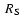 ,
proton heating (
,
proton heating (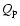 )
is negligible in the same region. However, the proton
temperature
)
is negligible in the same region. However, the proton
temperature 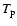 still increases substantially due to the
Coulomb coupling. After 1.4
still increases substantially due to the
Coulomb coupling. After 1.4
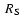 ,
the Coulomb coupling
between protons and alpha particles is not strong enough to
balance the adiabatic cooling of protons, and
,
the Coulomb coupling
between protons and alpha particles is not strong enough to
balance the adiabatic cooling of protons, and 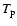 decreases. Beyond 2
decreases. Beyond 2
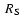 ,
alpha particles are fast, and
start partially to lose resonance with waves, and protons soon
absorb more energy from waves than do the alpha particles. At
2.5
,
alpha particles are fast, and
start partially to lose resonance with waves, and protons soon
absorb more energy from waves than do the alpha particles. At
2.5
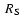 ,
the wave heating of protons finally
counterbalances adiabatic cooling and
,
the wave heating of protons finally
counterbalances adiabatic cooling and 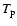 increases. Alpha
particles gradually lose resonance with waves and
increases. Alpha
particles gradually lose resonance with waves and 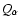 becomes very small above 3
becomes very small above 3
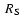 .
.
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{H4077F3.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg65.gif) |
Figure 3:
An enlarged version of Fig. 2 in the region just above
the lower boundary. |
The model calculation predicts a rather low proton temperature
between 2 and 4 solar radii. The local minimum 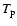 at
2.5
at
2.5
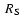 is only
is only
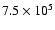 K, only slightly higher
than the electron temperature. However, the Alfvén wave
amplitude is strong (as will be shown in Fig. 6) in the region.
Hence, the effective proton temperature
K, only slightly higher
than the electron temperature. However, the Alfvén wave
amplitude is strong (as will be shown in Fig. 6) in the region.
Hence, the effective proton temperature
is still significant in the same distances (see the dashed-dotted
line in Fig. 2b). Here 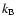 is the Boltzmann constant,
is the Boltzmann constant,
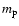 is the proton mass. The narrow vertical bars represent
the observed proton effective temperatures from UVCS spectral line
width measurements in a northern polar coronal hole reported by
Esser et al. (1999), while the wide vertical bars represent
similar observations in polar coronal holes reported by Kohl et
al. (1998). All these observations were made when the Sun was at its
phase of minimum activity. In general, the calculated proton
effective temperature matches observations reasonably well. Beyond
2
is the proton mass. The narrow vertical bars represent
the observed proton effective temperatures from UVCS spectral line
width measurements in a northern polar coronal hole reported by
Esser et al. (1999), while the wide vertical bars represent
similar observations in polar coronal holes reported by Kohl et
al. (1998). All these observations were made when the Sun was at its
phase of minimum activity. In general, the calculated proton
effective temperature matches observations reasonably well. Beyond
2
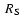 ,
the proton temperature is low, but the calculated
proton effective temperature is still very close to the observed
lowest effective temperatures or within the observed
uncertainties. Remember, the calculated effective proton
temperature from Model 1 does not include the line-width
broadening due to the outflow velocities along the line of sight,
and the ion temperature anisotropies are neglected. Also note, in
a two-fluid solar wind model, the proton effective temperatures
from model calculations are at the upper limit of observed proton
effective temperatures (Li et al. 1999). Future work to include
species temperature anisotropies may improve the match with
observations. This study suggests that the hydrogen Lyman alpha
lines observed by UVCS may be primarily broadened by Alfvén
waves, while spectral lines of minor ions may be primarily
broadened by thermal motions and outflow velocities along the line
of sight. The transverse velocity disturbance
,
the proton temperature is low, but the calculated
proton effective temperature is still very close to the observed
lowest effective temperatures or within the observed
uncertainties. Remember, the calculated effective proton
temperature from Model 1 does not include the line-width
broadening due to the outflow velocities along the line of sight,
and the ion temperature anisotropies are neglected. Also note, in
a two-fluid solar wind model, the proton effective temperatures
from model calculations are at the upper limit of observed proton
effective temperatures (Li et al. 1999). Future work to include
species temperature anisotropies may improve the match with
observations. This study suggests that the hydrogen Lyman alpha
lines observed by UVCS may be primarily broadened by Alfvén
waves, while spectral lines of minor ions may be primarily
broadened by thermal motions and outflow velocities along the line
of sight. The transverse velocity disturbance
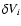 of ion
species i with outflow velocity vi is (Isenberg & Hollweg
1982)
of ion
species i with outflow velocity vi is (Isenberg & Hollweg
1982)
At 2-4 solar radii, minor ion velocity
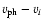 may be
a significant fraction of Alfvén phase velocity
may be
a significant fraction of Alfvén phase velocity
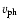 (for protons, the ratio
(for protons, the ratio
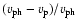 is
roughly 1). Hence the line-width broadening of minor ions from
waves is weakened.
The alpha particles lose resonance with Alfvén waves at
large distances, suggesting alpha particles (and perhaps other
minors too) must be heated by other mechanisms in interplanetary
space (plasma micro-instabilities may be the main sources).
is
roughly 1). Hence the line-width broadening of minor ions from
waves is weakened.
The alpha particles lose resonance with Alfvén waves at
large distances, suggesting alpha particles (and perhaps other
minors too) must be heated by other mechanisms in interplanetary
space (plasma micro-instabilities may be the main sources).
Note the wave amplitude at the base of the flux tube is 21 km s-1,
much smaller than the value used in Li (2002). The wave amplitude
is at the lower end observed by SUMER (Tu et al. 1998). However
SUMER observations were done above the solar limb. The coronal
funnels considered in this paper are deeply rooted in the lower
transition region, a smaller wave amplitude can be justified due
to the high density. By combining the solar wind acceleration and
the transition region in a full treatment, the heat deposited
below the subsonic point can increase mass fluxes substantially.
To produce a particle flux constrained by in situ measurements, a
smaller wave amplitude is necessary. This demonstrates that the
coronal heating along open field lines and the solar wind
acceleration must be treated as a single problem.
To show the transition region and the initial heating process more
clearly, Fig. 3 shows a small region above the lower boundary of
the solution in Fig. 2. When temperatures are still low, alpha
particles and protons have virtually the same speed (h<30 km). At
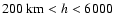 km, alpha particles are not only faster, but much
hotter than protons as well. The proton velocity at the lower
boundary is
km, alpha particles are not only faster, but much
hotter than protons as well. The proton velocity at the lower
boundary is
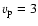 km s-1. The alpha particles reach a local
maximum velocity of 28 km s-1 at a height of 600 km. This effect is
totally due to the introduction of ion cyclotron resonance. Below
this point, the wave frequency at the high end of the spectrum is
still smaller than the frequency where alpha particles can
resonate with the waves. Hence no wave dissipation occurs. The
most interesting feature of Fig. 3 is that at the top of the
transition region or at the bottom of the corona, alpha particles
and protons (and electrons) can be significantly away from thermal
equilibrium. In the region
km s-1. The alpha particles reach a local
maximum velocity of 28 km s-1 at a height of 600 km. This effect is
totally due to the introduction of ion cyclotron resonance. Below
this point, the wave frequency at the high end of the spectrum is
still smaller than the frequency where alpha particles can
resonate with the waves. Hence no wave dissipation occurs. The
most interesting feature of Fig. 3 is that at the top of the
transition region or at the bottom of the corona, alpha particles
and protons (and electrons) can be significantly away from thermal
equilibrium. In the region
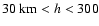 km, alpha particles are
slower than protons. This is because the higher temperature
gradient of alpha particles (compared with protons) actually
produces a negative pressure gradient force for alpha particles
(see Fig. 5), and alpha particles are slower than protons. Since
km, alpha particles are
slower than protons. This is because the higher temperature
gradient of alpha particles (compared with protons) actually
produces a negative pressure gradient force for alpha particles
(see Fig. 5), and alpha particles are slower than protons. Since
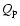 is negligible at h<105 km, protons and electrons are
heated by Coulomb coupling with protons and alpha particles, and
by the electron heat flux. The evolution of speed and temperatures
in Fig. 3 is similar to the results in Hackenberg et al. (2000).
The loss of thermal equilibrium between protons and electrons at
the top of transition region or the bottom of the corona has also
been found by Marsch & Tu (1997a) and Vocks & Marsch (2002).
Here it is shown that protons and alpha particles can also lose
thermal equilibrium in the same region. The transition region of
model 1 is very narrow: the jump of the electron temperature
is negligible at h<105 km, protons and electrons are
heated by Coulomb coupling with protons and alpha particles, and
by the electron heat flux. The evolution of speed and temperatures
in Fig. 3 is similar to the results in Hackenberg et al. (2000).
The loss of thermal equilibrium between protons and electrons at
the top of transition region or the bottom of the corona has also
been found by Marsch & Tu (1997a) and Vocks & Marsch (2002).
Here it is shown that protons and alpha particles can also lose
thermal equilibrium in the same region. The transition region of
model 1 is very narrow: the jump of the electron temperature 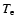 from
from
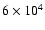 to
to
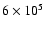 K takes place in
390 km.
K takes place in
390 km.
A few comments can be made about the velocity profile of alpha
particles in Fig. 3a. Transition region spectral line observations
often find various velocities of ions. These velocities can vary
from a few to about twenty kilometers per second. For instance,
Hassler et al. (1999) found that in network boundaries an average
outflow velocity is several kilometers per second when
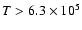 K, while Wilhelm et al. (2000) estimated that
the outflow velocity of Ne7+ is about 14 km s-1 along open
magnetic field lines from their SUMER data. The velocity of alpha
particles
K, while Wilhelm et al. (2000) estimated that
the outflow velocity of Ne7+ is about 14 km s-1 along open
magnetic field lines from their SUMER data. The velocity of alpha
particles 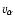 in Fig. 3a is in the range 3 km s
in Fig. 3a is in the range 3 km s
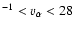 km s-1 at different heights. Even though no
other minor ions have been included in this investigation,
however, if those ions behave similar to the alpha particles,
their velocity is expected to vary in a similar manner. Hence, if
spectral lines are observed at different heights, observed outflow
velocities may vary accordingly.
km s-1 at different heights. Even though no
other minor ions have been included in this investigation,
however, if those ions behave similar to the alpha particles,
their velocity is expected to vary in a similar manner. Hence, if
spectral lines are observed at different heights, observed outflow
velocities may vary accordingly.
The fact that minor ions can flow much faster than the bulk plasma flow in
the upper transition region may have implications on the analysis of
transition region spectral line observations.
Traditional atomic physics calculations on which the diagnostics
of both temperatures and densities depend
often assume equal ion and electron temperatures. From Doppler
shift measurements of transition region spectral lines, Dere et al. (1989) found that the mass flux in the region is more than
enough to account for in situ measured solar wind mass flux. If
minor ions are indeed much faster than protons and electrons in
the transition region, one cannot safely determine the bulk
outflow velocity of plasmas in the region by using minor ion
outflow velocities.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H4077F4.ps}\end{figure}](/articles/aa/full/2003/28/aah4077/Timg82.gif) |
Figure 4:
Ratio between alpha particle heating term due to waves
and collisional heating terms in alpha particle energy energy
equation (Hu & Habbal 1999). |
Needless to say, in the region where no direct external heating is
added, the strong heating of the three species is entirely due to
the heat fluxes of the species and Coulomb coupling between them.
The Coulomb collisional coupling between ions is much stronger
than the coupling between ions and electrons. Hence protons and
alpha particles have identical temperatures. When the electron
temperature gradient becomes very large, electrons become hotter
than protons and alpha particles (h<10 km, Fig. 3b). This can be
easily understood since the classical electron thermal
conductivity is more than one magnitude larger than the classical
ion thermal conductivities. Note that the strong Coulomb coupling
makes the temperature difference less than 20% (at h<10 km).
This seems to make our assumption that species have the same
temperature at
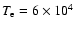 K questionable. However,
the electron heat conductivity is proportional to
K questionable. However,
the electron heat conductivity is proportional to
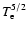 ,
the heat flux is relatively small at low temperatures. And
most importantly, Coulomb collisions become extremely strong at
low temperatures. This small discrepancy does not influence the
model solution in a significant way. To avoid this discrepancy,
future models need to include the chromosphere and the detailed
ionization processes of hydrogen and helium, which is beyond the
scope of this paper.
,
the heat flux is relatively small at low temperatures. And
most importantly, Coulomb collisions become extremely strong at
low temperatures. This small discrepancy does not influence the
model solution in a significant way. To avoid this discrepancy,
future models need to include the chromosphere and the detailed
ionization processes of hydrogen and helium, which is beyond the
scope of this paper.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{H4077F5.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg85.gif) |
Figure 5:
Model 1: thermal pressure of electrons (dotted line),
protons (thin solid line), and alpha particles (dashed line).
The thick solid line represents the total pressure
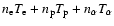 . . |
To show how the loss of thermal equilibrium between protons and
alpha particles can occur around h=1000 km in the model, R, the
ratio between 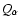 and proton/alpha Coulomb coupling terms
in the energy equation of the alpha particles, is plotted in Fig. 4. Clearly only in the region where |R| is significantly larger
than 1 do alpha particles lose thermal equilibrium with protons.
Note the rate R is negative, suggesting that alpha particles
lose thermal energy to protons due to collisions. At h<105 km,
roughly speaking, only alpha particles are directly heated by
waves. Without any other external heat sources, protons are only
heated via Coulomb coupling with alpha particles. Above
h=300 000 km (or about 1.4
and proton/alpha Coulomb coupling terms
in the energy equation of the alpha particles, is plotted in Fig. 4. Clearly only in the region where |R| is significantly larger
than 1 do alpha particles lose thermal equilibrium with protons.
Note the rate R is negative, suggesting that alpha particles
lose thermal energy to protons due to collisions. At h<105 km,
roughly speaking, only alpha particles are directly heated by
waves. Without any other external heat sources, protons are only
heated via Coulomb coupling with alpha particles. Above
h=300 000 km (or about 1.4
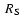 ), this ratio is much larger
than 1, suggesting that Coulomb coupling is not important.
), this ratio is much larger
than 1, suggesting that Coulomb coupling is not important.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H4077F6.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg86.gif) |
Figure 6:
Model 1: a) the Alfvén speed (solid line) and the wave
amplitude (dashed line); b) ratio
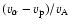 ;
c) Proton beta value. ;
c) Proton beta value. |
Figure 5 shows the species thermal pressures from the model in Fig. 2. The total thermal pressure is nearly a constant between
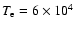 K and
K and
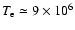 K. However,
the individual species pressures are not as constant. Ion
cyclotron resonance heating yields a large alpha thermal pressure
bump at
K. However,
the individual species pressures are not as constant. Ion
cyclotron resonance heating yields a large alpha thermal pressure
bump at
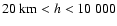 km.
km.
The Alfvén speed 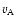 and Alfvén wave amplitude
and Alfvén wave amplitude
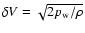 are shown in Fig. 6a. Here
are shown in Fig. 6a. Here 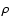 is the total plasma mass
density.
The Alfvén wave amplitude reaches 35 km s-1 at
is the total plasma mass
density.
The Alfvén wave amplitude reaches 35 km s-1 at
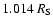 ,
and
,
and
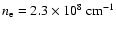 ,
,
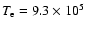 K.
The ratio
K.
The ratio
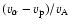 is shown
in Fig. 6b. To compare Fig. 6b with Fig. 2d,
the proton heating rate
is shown
in Fig. 6b. To compare Fig. 6b with Fig. 2d,
the proton heating rate 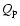 becomes larger than
becomes larger than 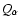 at about 2.7
at about 2.7
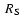 ,
where the ratio
,
where the ratio
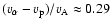 .
Note, if warm plasma dispersion relation is used, protons may get
more heating faster (Li & Habbal 1999). Hollweg & Isenberg
(2002) also discussed this issue. The "switch" from primarily
heating alpha particle to primarily heating protons depends on the
abundance of alpha particles, the plasma beta value and the
detailed dissipation range spectrum.
The proton beta value, the ratio between the proton thermal pressure and
magnetic pressure
.
Note, if warm plasma dispersion relation is used, protons may get
more heating faster (Li & Habbal 1999). Hollweg & Isenberg
(2002) also discussed this issue. The "switch" from primarily
heating alpha particle to primarily heating protons depends on the
abundance of alpha particles, the plasma beta value and the
detailed dissipation range spectrum.
The proton beta value, the ratio between the proton thermal pressure and
magnetic pressure
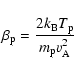 |
(7) |
is plotted in Fig. 6c. This value is small at
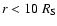 .
.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{H4077F7.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg97.gif) |
Figure 7:
Contributions to the energy flux density, multiplied
by
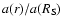 for Model 1: Alfvén wave energy flux (dashed);
total enthalpy (dotted); total kinetic energy flux (thin
solid); total heat flux (dot-dashed); gravity
(dash-triple-dotted); radiation (thick dashed). The thick
solid line is the total energy flux density.
for Model 1: Alfvén wave energy flux (dashed);
total enthalpy (dotted); total kinetic energy flux (thin
solid); total heat flux (dot-dashed); gravity
(dash-triple-dotted); radiation (thick dashed). The thick
solid line is the total energy flux density. |
Figure 7 shows the various contributions to the energy flux, scaled
to the inner boundary. The total energy flux is a sum of the
Alfvén wave energy flux; kinetic energy flux of protons and
alpha particles; gravitational energy flux; total enthalpy flux;
total heat flux of electrons, protons and alpha particles; and the
radiation loss (an integration from 1
 to a given
distance). It is obvious that the radiation loss is a small
quantity in the energy budget. The heat flux is only important in
the transition region. The total energy flux is a straight
horizontal line, indicating an excellent energy conservation. In
fact, the maximum relative error in the total energy flux is
0.16%, which is too small to be seen in Fig. 7.
to a given
distance). It is obvious that the radiation loss is a small
quantity in the energy budget. The heat flux is only important in
the transition region. The total energy flux is a straight
horizontal line, indicating an excellent energy conservation. In
fact, the maximum relative error in the total energy flux is
0.16%, which is too small to be seen in Fig. 7.
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{H4077F8.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg99.gif) |
Figure 8:
A small region just above the lower boundary for Model 2.
Here
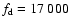 Hz. Hz. |
From Figs. 3 and 4, it is seen that alpha particles lose thermal
equilibrium with protons around h=1000 km when the heat gain that
the alpha particles obtained from waves is much more than the heat
loss through the Coulomb coupling with protons. In this region,
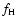 decreases most rapidly with height due to the fast
flux tube expansion. If the wave heating begins at an even higher
location in the coronal funnel, for instance, the wave heating
starts after the first flux tube expansion almost ends,
the heating rate
decreases most rapidly with height due to the fast
flux tube expansion. If the wave heating begins at an even higher
location in the coronal funnel, for instance, the wave heating
starts after the first flux tube expansion almost ends,
the heating rate 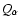 will be smaller since
will be smaller since
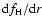 now is smaller and there is less wave energy at the high
frequency end. One of course expects that the loss of an
equilibrium between alpha particles and protons is going to be
weaker. This is exactly the case when the wave frequency at the
high end of the spectrum
now is smaller and there is less wave energy at the high
frequency end. One of course expects that the loss of an
equilibrium between alpha particles and protons is going to be
weaker. This is exactly the case when the wave frequency at the
high end of the spectrum 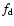 is 17 000 Hz. The overall
feature of this case is similar to those in Fig. 2 and will not be
shown here. The region just above the lower boundary is shown in
Fig. 8. The ion cyclotron heating is not introduced until at a
height 2070 km above the lower boundary (Fig. 8d). Even though the
wave heating still leads to different alpha particle and proton
temperatures at
is 17 000 Hz. The overall
feature of this case is similar to those in Fig. 2 and will not be
shown here. The region just above the lower boundary is shown in
Fig. 8. The ion cyclotron heating is not introduced until at a
height 2070 km above the lower boundary (Fig. 8d). Even though the
wave heating still leads to different alpha particle and proton
temperatures at
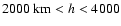 km (Fig. 8d), the difference is far
less significant than in Fig. 3b. There is virtually no velocity
difference in this region. Plasma species are roughly in thermal
equilibrium at h<105 km (Figs. 8a and 8b). The temperatures of
Model 2 in the transition region below 5000 km are much lower than
in model 1 (see Figs. 3b and 7b). However, Model 2 has a slightly
lower maximum electron temperature (
km (Fig. 8d), the difference is far
less significant than in Fig. 3b. There is virtually no velocity
difference in this region. Plasma species are roughly in thermal
equilibrium at h<105 km (Figs. 8a and 8b). The temperatures of
Model 2 in the transition region below 5000 km are much lower than
in model 1 (see Figs. 3b and 7b). However, Model 2 has a slightly
lower maximum electron temperature (
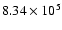 K, compared
to
K, compared
to
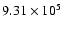 K in model 1). Although electrons are not
directly heated, these maximum
K in model 1). Although electrons are not
directly heated, these maximum 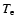 match SUMER
observations in coronal holes (Wilhelm et al. 1998). Overall, the
difference between Model 1 and Model 2 is marginal except in the
transition region.
match SUMER
observations in coronal holes (Wilhelm et al. 1998). Overall, the
difference between Model 1 and Model 2 is marginal except in the
transition region.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{H4077F9.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg105.gif) |
Figure 9:
Proton particle flux density (solid line) at the lower
computation boundary, proton speed (dashed line) at
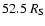 ,
and the transition region height (see text),
as a function of ,
and the transition region height (see text),
as a function of 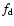 . .
|
Figure 9 shows the proton particle flux density at 1
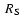 ,
the
proton velocity at 52.5
,
the
proton velocity at 52.5
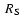 ,
and the height of the
transition region (defined as the distance over which the electron
temperature increases from
,
and the height of the
transition region (defined as the distance over which the electron
temperature increases from
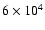 to
to
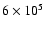 K), as a
function of
K), as a
function of 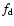 ,
other parameters are the same as used in
Model 1. Once the wave amplitude at the lower boundary and the
magnetic field geometry are chosen, the total energy flux entering
the computational domain is fixed (the only energy losses are heat
flux and radiation loss). However, if
,
other parameters are the same as used in
Model 1. Once the wave amplitude at the lower boundary and the
magnetic field geometry are chosen, the total energy flux entering
the computational domain is fixed (the only energy losses are heat
flux and radiation loss). However, if 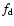 is smaller than
10 000 Hz, a steady state solution can not be obtained. The reason
is that as
is smaller than
10 000 Hz, a steady state solution can not be obtained. The reason
is that as 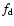 is small, the electron temperature gradient
becomes smaller. The transition region becomes too wide so the
electron heat flux is unable to balance the local radiation
loss. Hence a steady state hot corona and wind cannot be found.
(Note, however, if the chromosphere is also included in the model
calculation, the position of transition region may change as the
position of the energy deposit changes. But this is beyond the
scope of the present study.) Of course, if the wave power at high
frequency is enhanced, as suggested by Tu & Marsch (1997), the
result may be different. Roughly speaking, the proton mass flux is
almost constant (the change is less than 10%), although the
plasma parameters at the coronal base can be very different as
shown in Figs. 3 and 8. The small variation reflects the different
heat flux losses to the chromosphere: about 8.6% of the total
Alfvén wave energy flux (deposited between 1 and 52.5
is small, the electron temperature gradient
becomes smaller. The transition region becomes too wide so the
electron heat flux is unable to balance the local radiation
loss. Hence a steady state hot corona and wind cannot be found.
(Note, however, if the chromosphere is also included in the model
calculation, the position of transition region may change as the
position of the energy deposit changes. But this is beyond the
scope of the present study.) Of course, if the wave power at high
frequency is enhanced, as suggested by Tu & Marsch (1997), the
result may be different. Roughly speaking, the proton mass flux is
almost constant (the change is less than 10%), although the
plasma parameters at the coronal base can be very different as
shown in Figs. 3 and 8. The small variation reflects the different
heat flux losses to the chromosphere: about 8.6% of the total
Alfvén wave energy flux (deposited between 1 and 52.5 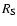 )
flows back to the chromosphere, while only less than 2.8% of
the Alfvén wave energy flux flows back to the chromosphere in
Model 2. Hence a smaller
)
flows back to the chromosphere, while only less than 2.8% of
the Alfvén wave energy flux flows back to the chromosphere in
Model 2. Hence a smaller 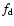 means more energy flux will
be available for the solar wind acceleration, and a smaller
particle flux and a faster wind may result (Leer & Holzer 1980).
Note, the height of the transition region changes more
dramatically as
means more energy flux will
be available for the solar wind acceleration, and a smaller
particle flux and a faster wind may result (Leer & Holzer 1980).
Note, the height of the transition region changes more
dramatically as 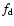 changes.
changes.
![\begin{figure}
\par\includegraphics[width=15.1cm,clip]{H4077F10.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg107.gif) |
Figure 10:
A small region just above the lower boundary for
Model 3. Here
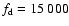 Hz. Hz. |
Finally we briefly present Model 3 with a much weaker magnetic
flux concentration in the supergranule convection zone boundaries.
In Model 3,
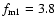 and the magnetic field at the lower
boundary is B0=36.1 G, so the magnetic field in interplanetary
space is unchanged. Again the overall large scale velocity and
temperature profiles (Model 3) are very close to Models 1 and 2
except a small region above the lower boundary, so only the region
above the lower boundary is shown in Fig. 10. Because at the base
of the corona,
and the magnetic field at the lower
boundary is B0=36.1 G, so the magnetic field in interplanetary
space is unchanged. Again the overall large scale velocity and
temperature profiles (Model 3) are very close to Models 1 and 2
except a small region above the lower boundary, so only the region
above the lower boundary is shown in Fig. 10. Because at the base
of the corona,
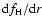 is much smaller than in model 1,
and there is less wave energy available for alpha particles below
1.1 solar radii (h<105 km). This leads to a much colder corona
below 1.1 solar radii and a less steep transition region (The
maximum electron temperature is
is much smaller than in model 1,
and there is less wave energy available for alpha particles below
1.1 solar radii (h<105 km). This leads to a much colder corona
below 1.1 solar radii and a less steep transition region (The
maximum electron temperature is
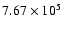 K.). Once again,
species are in thermal equilibrium in the transition region
(h<105 km). One noticeable feature of this model is that the
flow speed at
K.). Once again,
species are in thermal equilibrium in the transition region
(h<105 km). One noticeable feature of this model is that the
flow speed at
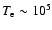 K level is quite small (less
than 5 km s-1). The transition region is wide: the electron
temperature increases from
K level is quite small (less
than 5 km s-1). The transition region is wide: the electron
temperature increases from
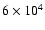 K to
K to
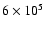 K in a
distance of 3300 km.
K in a
distance of 3300 km.
The model also produces reasonable proton particle flux:
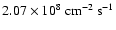 .
This model
actually produces a faster wind than in Fig. 2. This can be
understood since less wave energy is released just above the
transition region, and the electron heat flux down to the region
.
This model
actually produces a faster wind than in Fig. 2. This can be
understood since less wave energy is released just above the
transition region, and the electron heat flux down to the region
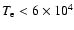 K is also smaller. Hence more wave energy
flux becomes available for the solar wind acceleration. There is
less energy at high frequencies suggesting less heat will be
deposited in the subsonic region, leading to a faster but diluter
wind (Leer & Holzer 1980). It is found that if
K is also smaller. Hence more wave energy
flux becomes available for the solar wind acceleration. There is
less energy at high frequencies suggesting less heat will be
deposited in the subsonic region, leading to a faster but diluter
wind (Leer & Holzer 1980). It is found that if
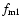 is
further decreased, with the same Alfvén wave amplitude, a steady
state solution of a corona and wind can not be obtained.
is
further decreased, with the same Alfvén wave amplitude, a steady
state solution of a corona and wind can not be obtained.
Plasma heating in coronal funnels along open magnetic field lines
by parallel propagating ion cyclotron waves is investigated in a
three-fluid approach. It is shown that the Coulomb coupling
between alpha particles and protons/electrons is strong enough to
produce a sharp transition region and a hot corona by heating
alpha particles alone. As shown by previous studies (Marsch & Tu
1997a,b; Tu & Marsch 1997; Hackeberg et al. 2000; Li 2002), a
spectrum of ion cyclotron waves of wave spectrum index -1 is
able to produce a transition region, a hot corona and to drive a
fast solar wind if the wave spectrum extends to the ion cyclotron
frequency range and the magnetic flux concentration in the
super-granule convection zone boundaries is sufficiently strong.
It is shown for the first time that by heating alpha particles
alone, a sharp transition region, a hot corona and basically a
fast solar wind can be produced. Hence, heavy ions may play a
crucial role in the corona heating and the solar wind acceleration
(Li et al. 1997).
It is found that the highest frequency of the waves, or the
location of the heating determines whether a thermal equilibrium
can be established between minor ions and protons. As the maximum
frequency is increased, alpha particles and protons end up farther
away from thermal equilibrium. As the maximum frequency becomes
smaller, alpha particles and protons are more likely to be in
thermal equilibrium. However, if the maximum frequency is below a
critical value, ion cyclotron resonance occurs far away from the
transition region and a hot corona cannot be produced. The fact
that heating alpha particles alone can produce a hot corona and
wind has interesting implications on the theory of coronal heating
and expansion. This study suggests that a corona can be created by
solely heating minor ions. Of course, the coronal heating physics
may be far more complicated than this study shows. Since there are
many ions heavier than the alpha particles in the transition
region and their gyro-frequencies are smaller than the
gyro-frequency of alpha particles, those heavy ions will be heated
first if parallel propagating ion cyclotron waves indeed are
responsible for the coronal heating. Since the abundances of those
minor ions are so small in the transition region and corona, it
remains an open question whether the Coulomb coupling is able to
efficiently transfer the energy from these minor ions to the major
species (protons and electrons) (see Cranmer 2000; Hollweg &
Isenberg 2002).
For simplicity, fixed velocity distributions and spectra in the
dissipation range are assumed. Tu & Marsch (2001) have pointed
out that due to cyclotron resonance, it is impossible for the
spectrum to maintain a rigid shape. Ion cyclotron resonance may
make the wave spectrum to have a cutoff at higher wave-numbers (Li
et al. 2001). Physically, a sufficiently high spectral index shall
mimic this effect. Since we have already taken a quite large
spectral index -5 in the dissipation range, a larger spectral
index is not going to change model results presented in this
study. The energy distribution between protons and alpha particles
is mainly determined by the dispersion relation. The model results
are not sensitive to the dissipation range spectral index in this
study. However the assumption of a fixed spectrum and velocity
distribution may give unrealistic energy distributions between
species. To tackle the wave heating problem in the corona,
self-consistent spectral evolution including wave dispersion and
kinetic treatment of particles are needed. The issue is currently
under study by many authors (Tam & Chang 1999; Galinsky &
Shevchenko 2000; Isenberg et al. 2000, 2001; Vocks & Marsch 2001,
2002).
This study may have implications on the solar wind charge state
investigations. By assuming plasma species in thermal equilibrium,
coronal electron temperature can be calculated using charge
fraction information from in situ charge state measurements.
However, those calculations found that the coronal electron
temperature above coronal holes is much higher than the electron
temperature observed by SUMER (see, Ko et al. 1997; Esser et al.
1998). Since this investigation suggests that ions in the
transition region may be already out of thermal equilibrium and
have different velocities, the contradiction between SUMER and
charge state calculations may be due to the loss of equilibrium in
the transition region and corona. Recently, Esser & Edgar (2001)
found that the velocity difference can significantly reduce the
discrepancy between observed in situ ion fractions and low coronal
temperatures.
We have neglected the temperature anisotropy of species in this
study and have adopted a collision dominated standard transport
equations and modified classical thermal conduction for the
three-fluid modelling. One has to recognize that it is still an
open question to what degree the treatment is valid. Certainly
Coulomb collisions are playing a major role in the transition
region. As the plasma density deceases rapidly with an increasing
height, collisions become less important in the inner corona.
During the transition from collision dominated regime to
collisionless regime, a refined description of species heat flux
is needed. The heat flux of ions may also play a role in shaping
the temperature anisotropy of the ions (Olsen et al. 1998; Olsen
& Leer 1999; Li 1999; Lie-Svendsen et al. 2001).
A complete treatment to include species temperature anisotropies
using high moment transport equations is under way.
Acknowledgements
This work is supported by PPARC rolling grant to University of Wales at
Aberystwyth. Part of the work was supported by the grant
NAG5-10873 to Smithsonian Astrophysical Observatory (SAO).
- Axford, W. I., & McKenzie, J. F. 1995, Solar wind
8, ed. D. Winterhalter, J. T. Gosling, S. R. Habbal, W. S. Kurth, & M.
Neugebauer, AIP, Dana Point, CA, p. 31
- Axford, W. I., McKenzie, J. F., et al. 1999, Space Sci.
Rev., 87, 25
NASA ADS
- Bavassano, B., Dobrowolny, M., Mariani, F., & Ness,
N. F. 1982, J. Geophys. Res., 87, 3617
NASA ADS
- Belcher, J. W., & Davis, L., Jr. 1971, J.
Geophys. Res., 76, 3534
- Braginskii, S. I. 1965, in Reviews of Plasma Physics, 1, 204
- Cranmer, S. R. 2000, ApJ, 532, 1197
NASA ADS
- Cranmer, S. R., Kohl, J. L., Noci, G., et al. 1999a, ApJ, 511, 481
NASA ADS
- Dere, K. P., Bartoe, J.-D. F., Brueckner, G. E., & Recely, F.,
ApJ, 345, L95
- Dowdy, J. F., Robin, D., & Moore, R. L. 1986, Sol. Phys., 105, 35
NASA ADS
- Dusenberg, P. B., & Hollweg, J. V. 1981, J. Geophys. Res., 86, 153
NASA ADS
- Esser, R., Edgar, R. J., & Brickhouse, N. S. 1998, ApJ, 498, 448
NASA ADS
- Esser, R., Fineschi, S., Dobrzycka, D., et al. 1999, ApJ, 510,
L63
NASA ADS
- Esser, R., & Edgar, R. J. 2001, ApJ, 563, 1055
NASA ADS
- Gabriel, A. H. 1976, Phil. Trans. R. Roc. Lond. A., 281,
339
NASA ADS
- Hackenberg, P., Mann, P., & Marsch, E. 2000, A&A, 360, 1139
NASA ADS
- Hansteen, V. H., & Leer, E. 1995, J. Geophys. Res., 100,
21, 577
- Hansteen, V. H., Leer, E., & Holzer, T. E. 1997,
ApJ, 482, 498
NASA ADS
- Hassler, D. M., Dammasch, I. E., Lemaire, P., et al. 1999, Science, 283, 810
NASA ADS
- Hollweg, J. V. 1986, J. Geophys. Res., 91, 4111,
NASA ADS
- Hollweg, J. V., & Johnson, W. 1988, J. Geophys. Res., 93, 9547
NASA ADS
- Hollweg, J. V., & Isenberg, P. A. 2002, J. Geophys.
Res., 107(A7), 1147
- Horbury, T. A., Balogh, A., Forsyth, R. J., & Smith, E. J.
1995, Ann. Geophys., 13, 105
NASA ADS
- Hu, Y. Q., & Habbal, S. R. 1999, J. Geophys. Res.,
104, 17045
- Hu, Y. Q., Esser, R., & Habbal, S. R. 1997, J. Geophys. Res.,
102, 14, 661
- Hu, Y. Q., Habbal, S. R., & Li, X. 1999, J. Geophys.
Res., 104, 24819
- Hu, Y. Q., Esser, R., & Habbal, S. R. 2000, J.
Geophys. Res., 105, 2093
- Isenberg, P. A. 1990, J. Geophys. Res., 95,
6437
NASA ADS
- Isenberg, P. A., & Hollweg, J. V. 1982, J. Geophys. Res., 87, 5023
NASA ADS
- Isenberg, P. A., & Hollweg, J. V. 1983,
J. Geophys. Res., 88, 3923
NASA ADS
- Isenberg, P. A., Lee, M. A., & Hollweg, J. V.
2000, Sol. Phys., 193, 247
NASA ADS
- Isenberg, P. A., Lee, M. A., & Hollweg, J. V. 2001, J. Geophys. Res., 106,
5649
NASA ADS
- Kohl, J. L., Noci, G., Antonucci, E., et al. 1998, ApJ, 501, L127
NASA ADS
- Kopp, R. A., & Holzer, T. E. 1976, Sol. Phys., 49, 43
NASA ADS
- Leer, E., & Holzer, T. E. 1980, J. Geophys. Res., 85, 4681
NASA ADS
- Li, X. 1999, J. Geophys. Res., 104, 19, 773
- Li, X. 2002, ApJ, 571, L67
NASA ADS
- Li, X., & Habbal, S. R. 1999, Sol. Phys., 190, 485
NASA ADS
- Li, X., Habbal, S. R., & Hu, Y. Q. 1997, J. Geophys. Res.,
102, 17, 419
- Li, X., Habbal, S. R., Kohl, J., & Noci, G. 1998, ApJ, 401, 133
- Li, X., Habbal, S. R., Hollweg, J. V., & Esser, R. 1999,
J. Geophys. Res., 104, 2521
NASA ADS
- Li, H., Gary, P. S., & Stawicki, O. 2001, Geophys. Res. Lett., 28,
1347
NASA ADS
- Lie-Svendsen, O., Leer, E., & Hansteen, V. H. 2001, J. Geophys. Res.,
106, 8217
NASA ADS
- Lie-Svendsen, O., Hansteen, V. H., &
Leer, E. 2002, ApJ,
- Marsch, E. 1999, Space Sc. Rev., 87, 1
NASA ADS
- Marsch, E., & Tu, C. Y. 1990, J. Geophys. Res.,
95, 8211
NASA ADS
- Marsch, E., & Tu, C. Y. 1997a, Sol. Phys., 176, 87
NASA ADS
- Marsch, E., & Tu, C. Y. 1997b, A&A, 319, L17
NASA ADS
- Marsch, E., Goertz, C. K., & Richter, A. K. 1982, J. Grophys. Res.,
87, 5030
NASA ADS
- McKenzie, J. F., Banaszkiewicz, M., & Axford,
W. I. 1995, A&A, 303, 45
- McKenzie, J. F., Axford, W. I., & Banaszkiewicz,
M. 1997, Geophys. Res. Lett., 24, 2877
NASA ADS
- Olsen, E. L., Leer, E., & Lie-Svendsen, O. 1998, A&A, 338, 747
NASA ADS
- Olsen, E. L., & Leer, E. 1999, J. Geophys. Res., 104, 9963
NASA ADS
- Phillips, J. L., Bame, S. J., Feldman, W. C., et al. 1995, Science, 268, 1030
NASA ADS
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 503, 475
NASA ADS
- Smith, E. J., Balogh, A., Neugebauer, M., & McComas,
D. 1995, Geophys. Res. Lett., 22, 3381
NASA ADS
- Spitzer, L., Jr. 1962, Physcis of Fully Ionized Gases (New York: Interscience)
- Tam, S. W. Y., & Chang, T. 1999, Geophys. Res.
Lett., 26, 3189
NASA ADS
- Tu, C.-Y. 1987, Sol. Phys., 109, 149
NASA ADS
- Tu, C.-Y. 1988, J. Geophys. Res., 93, 7
NASA ADS
- Tu, C.-Y., Pu, Z. Y., & Wei, F. S. 1984, J. Geophys. Res., 94, 11, 739
- Tu, C.-Y., & Marsch, E. 1997, Sol. Phys., 171, 363
NASA ADS
- Tu, C.-Y., Marsch, E., Wilhelm, K., & Curdt, W. 1998,
ApJ, 503, 475
NASA ADS
- Tu, C.-Y., & Marsch, E. 2001, J. Geophys. Res., 106,
8233
NASA ADS
- Vocks, C., & Marsch, E. 2001,
Geophys. Res. Lett., 28, 1917
NASA ADS
- Vocks, C., & Marsch, E. 2002, ApJ, 568, 1030
NASA ADS
- Warren, H. P., & Hassler, D. M. 1999, J. Geophys.
Res., 104, 9781
NASA ADS
- Wilhelm, K., Marsch, E., Dwivedi, B. N., et al.
1998, ApJ, 500, 1023
NASA ADS
- Wilhelm, K., Dammasch, I. E., Marsch, E., &
Hassler, D. M. 2000, A&A, 353, 749
NASA ADS
Copyright ESO 2003
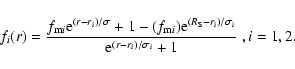
![\begin{displaymath}\begin{array}{l}
\kappa_{\rm e}=7.8\times10^{-7}T^{5/2}_{\rm ...
...{\rm S} \over \xi R_{\rm S}} \right)^2 \right]\cdot
\end{array}\end{displaymath}](/articles/aa/full/2003/28/aah4077/img20.gif)

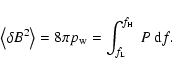
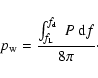

![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{H4077F1.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg54.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{H4077F2.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{H4077F3.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg65.gif)
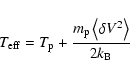
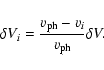
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H4077F4.ps}\end{figure}](/articles/aa/full/2003/28/aah4077/Timg82.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{H4077F5.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H4077F6.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg86.gif)
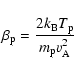
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{H4077F7.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{H4077F8.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg99.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{H4077F9.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg105.gif)
![\begin{figure}
\par\includegraphics[width=15.1cm,clip]{H4077F10.ps} \end{figure}](/articles/aa/full/2003/28/aah4077/Timg107.gif)