A&A 406, 37-41 (2003)
DOI: 10.1051/0004-6361:20030778
K. A. Malik1 - D. R. Matravers2
1 -
GRECO, Institut d'Astrophysique de Paris, CNRS,
98bis Boulevard Arago,
75014 Paris, France
2 -
Institute of Cosmology and Gravitation,
University of Portsmouth, Portsmouth PO1 2EG,
UK
Received 16 January 2003 / Accepted 12 May 2003
Abstract
We extend the Kelvin-Helmholtz instability to an expanding
background. We study the evolution of
a non-viscous irrotational fluid and find that for wavelengths
much smaller than the Hubble scale small perturbations of
the fluid are unstable for wavenumbers larger than a critical
value. We then apply this result in the early universe,
treating cold dark matter as a
classical fluid with vanishing background pressure.
Key words: instabilities - cosmology: theory - cosmology: dark matter
In the standard cosmological model quantum fluctuations are magnified from microscopic to cosmological scales during a period of exponential expansion (inflation) and source curvature perturbations with a scale-invariant or nearly scale-invariant spectrum (Kolb & Turner 1990; Liddle & Lyth 2000). After inflation these perturbations act as seeds for the large scale structure of the universe: first, beginning during radiation domination, non-baryonic dark matter "falls'' into the potential wells formed during inflation and later, during matter domination but after decoupling, radiation and baryonic matter follow.
In this picture radiation and baryonic matter can "fall'' into the potential wells only after decoupling since before that their Jeans length is larger than the Hubble radius. After decoupling perturbations whose wavelength is larger than the Jeans-length grow, but on scales smaller than the Jeans-length they oscillate, leaving imprints in the CMB that can be observed today. On very small scales structure is wiped out through the tight coupling of the baryons to the photons until decoupling (Silk 1968). Unlike in baryonic matter and radiation, perturbations in the non-baryonic dark matter can start growing as soon as their wavelength is smaller than the horizon, since the Jeans scale is negligible for non-interacting dark matter. The non-baryonic dark matter can therefore cluster and "fall'' into the potential wells much earlier than the other matter.
In fluid dynamics the study of instabilities (Chandrasekhar 1981) is well established and has also been extended to the astrophysical context (see Inogamov 1999, and references therein). The Kelvin-Helmholtz instability has been known for nearly 150 years (Chandrasekhar 1981). In its simplest form two large fluid volumes, separated by an interface, move in opposite directions. Neglecting the stabilizing effects of density and gravity gradients this setup is unstable for all non-zero velocities and wavenumbers.
We study the initial stages in the evolution of small perturbations in an irrotational, non-viscous fluid due to a Kelvin-Helmholtz instability in an expanding universe. We show that even in such a background these instabilities occur. We then apply these results in the early universe. Two large colliding regions of cold dark matter might serve as an example: the Kelvin-Helmholtz instability can arise at the contact surfaces of the two regions. We model the dark matter as a fluid with vanishing background pressure in concordance with the standard cold dark matter models (Kolb & Turner 1990; Liddle & Lyth 2000). Depending on when this happens in the evolution of the background the perturbations arising from the instability grow either exponentially or linearly on scales smaller than a critical wavenumber which we determine. On the basis of these results we argue that it will be interesting to test these perturbations in simulations because they could have relevance to the dark matter cusp and halo problems and to anisotropies in the CMB.
In the next section we give the governing equations for the fluid. In Sect. 3 we specify the model geometry and the general setup. After giving the background solution in Sect. 4, we derive the perturbed equations in Sect. 5 and analyse the stability of the system. In Sect. 6 we then calculate the critical wavenumbers for which instability can occur. We apply our results to standard cold dark matter in the final section and discuss possible implications.
We are interested in the dynamics of a fluid in the early universe on
scales much smaller than the horizon size, i.e.
![]() .
We
can therefore use a Newtonian approximation on an expanding background
where only the background expansion is described by a flat FRW model
(Kolb & Turner 1990; Liddle & Lyth 2000).
.
We
can therefore use a Newtonian approximation on an expanding background
where only the background expansion is described by a flat FRW model
(Kolb & Turner 1990; Liddle & Lyth 2000).
We assume that the fluid is non-viscous and irrotational, its dynamics therefore governed by the Euler equation. The fluid does not have to be the only or dominant matter component in the model of the universe, we merely require that it does not interact with the other fluids such as radiation. As outlined above we envisage this fluid to describe standard cold dark matter, which has vanishing background pressure. We shall nevertheless keep the discussion in this and the following sections applicable to the general case of a perfect fluid and restrict the analysis to cold dark matter only when we consider a particular example in the final section.
The Euler equation in an expanding background is given by
(Peebles 1980)
We can split the variables describing our problem into
a time-dependent background part and time- and
space-dependent first order perturbations,
The geometry of our model is outlined in
Fig. 1: two large volumes
of fluid are separated by an interface at x3=0 and move in
opposite directions with velocities ![]() and
and ![]() above and below the interface, respectively. We allow for a
perturbation of the fluid interface separating the two flows which
is denoted by
above and below the interface, respectively. We allow for a
perturbation of the fluid interface separating the two flows which
is denoted by
![]() .
.
The velocity can also be split according to Eq. (4), ui = Ui+vi, where Ui is the background part and vi the perturbation. Without loss of generality we can choose our coordinate system such that the x1-coordinate is aligned with the direction of the background flow as in Fig. 1. The background flow is therefore separated by the x3=0 plane. The background velocity Ui has then only one non-zero component U1=U(t), but for the velocity perturbation we still have vi=vi(t,xi).
We neglect gravitational back reaction on the perturbations and
therefore set
![]() ,
i.e. the gravitational potential
,
i.e. the gravitational potential
![]() only has a time-dependent zeroth order part.
only has a time-dependent zeroth order part.
| |
Figure 1:
The configuration: fluid
moving to the left with velocity
|
For the background described in the previous section
we get from Eqs. (1) and (2)
the simple background Euler and energy conservation
equations
The background expansion is described by a FRW model.
We therefore get a power law solution for the
scale factor (Kolb & Turner 1990; Liddle & Lyth 2000)
In order to analyze the stability of our model we first linearize the governing equations and then look for growing mode solutions.
Linearizing around the background described in
Sect. 3 we get
from Eq. (1) the linearized perturbed
Euler equation to first order
The perturbation in the position of the interface,
given by
![]() ,
is a first order
quantity and has to be included in our analysis.
The velocity of the fluid interface
in the 3-direction is given by
,
is a first order
quantity and has to be included in our analysis.
The velocity of the fluid interface
in the 3-direction is given by
We now integrate Eq. (17) across the interface from
![]() to
to
![]() and then let
and then let
![]() to get
to get
Note that we recover the standard result of Chandrasekhar (Chandrasekhar 1981), i.e. that all wavenumbers are exponentially unstable, if we set a=1.
Equation (20) can now be integrated using the solution for
the background velocity Eq. (7) and the scale factor
Eq. (8). We have
![]() where we have
defined
where we have
defined
![]() .
We choose
as initial condition that there is no amplification
at the beginning, i.e.
.
We choose
as initial condition that there is no amplification
at the beginning, i.e. ![]() at t=t0.
at t=t0.
We study the case of a radiation dominated universe,
i.e.
![]() ,
and a universe with a different
exponent
,
and a universe with a different
exponent ![]() separately.
separately.
Integrating the real part of Eq. (20)
we get for the case
![]()
In the case where
![]() we get, by integrating the
real part of Eq. (20),
we get, by integrating the
real part of Eq. (20),
We can now analyze the solutions we have found in the previous section and calculate the critical wavenumber beyond which the perturbations are growing.
In the radiation dominated regime,
![]() ,
we find from Eq. (21) and our ansatz (14)
that the flow is linearly unstable for all wavenumbers with
,
we find from Eq. (21) and our ansatz (14)
that the flow is linearly unstable for all wavenumbers with
In the case of
![]() the behavior of the perturbations is more
complicated than in the radiation dominated case,
since here the critical wave number is time dependent.
the behavior of the perturbations is more
complicated than in the radiation dominated case,
since here the critical wave number is time dependent.
The solution Eq. (22) has two parts with
different behaviors:
the logarithmic part will always lead to a decrease in ![]() ,
whereas the second term behaves differently depending
on whether
,
whereas the second term behaves differently depending
on whether ![]() is smaller or larger than 1/2.
In the case
is smaller or larger than 1/2.
In the case
![]() the second term is always
increasing and will dominate after a finite time for
large enough wavenumbers.
For
the second term is always
increasing and will dominate after a finite time for
large enough wavenumbers.
For
![]() the second term in Eq. (22) will
first increase and then decrease but can lead to instability if it
dominates for a long enough period.
From Eq. (22) the critical wavenumber
for which small perturbations begin to grow is
the second term in Eq. (22) will
first increase and then decrease but can lead to instability if it
dominates for a long enough period.
From Eq. (22) the critical wavenumber
for which small perturbations begin to grow is
We will now discuss the two cases
![]() and
and
![]() separately.
separately.
The case
![]() is particularly simple. Using the relation
(Abramowitz & Stegun 1972)
is particularly simple. Using the relation
(Abramowitz & Stegun 1972)
From Eq. (25) we see that for large ![]() the
time dependent term
the
time dependent term
![]() tends to
tends to
![]() .
Hence, in this case, the critical wave
number increases with time. In order to get a conservative
estimate of the critical wavenumber we evaluate
Eq. (25) at the time when a given perturbation is
largest.
.
Hence, in this case, the critical wave
number increases with time. In order to get a conservative
estimate of the critical wavenumber we evaluate
Eq. (25) at the time when a given perturbation is
largest.
The perturbations reach their maximum value at
Our model covers the irrotational, non-viscous case. The inclusion of viscosity is even more complicated: for small Reynolds numbers it tends to dampen the instability, whereas for large Reynolds numbers the development of turbulence becomes more likely. Although the simplest CDM model does not include viscosity there are models, like neutralino dark matter studied in (Hofmann et al. 2001), which are viscous. We note these instabilities will probably not be detected in models based on collision-free Boltzmann distributions and that the fluid model we use will break down at some small scale dependent on the dark matter properties.
In standard fluid dynamics the Kelvin-Helmholtz instability in the
incompressible case develops for all wavenumbers k>0. However in
an expanding universe we have shown that this is no longer the
case and that there are critical wave numbers which separate
stable and unstable domains. These wave numbers depend on the
expansion of the background and the background velocity. For
wave numbers larger than the critical wavenumber,
![]() ,
small perturbations will grow.
,
small perturbations will grow.
More specifically, for a scale factor exponent
![]() perturbations will grow for a wavenumber-dependent time. In the
case
perturbations will grow for a wavenumber-dependent time. In the
case
![]() ,
i.e. during radiation domination, perturbations
grow linearly for all times and for
,
i.e. during radiation domination, perturbations
grow linearly for all times and for
![]() they grow
exponentially for all times.
they grow
exponentially for all times.
As an illustration we look at the case of cold dark matter
at the beginning of matter domination,
![]() .
The physical setting could be two large volumes of cold dark matter
colliding or some non-homogeneous velocity flows in the early
universe. In the first case the contact surface would be prone to the
Kelvin-Helmholtz instability and in the second the instability would
occur inside the flow.
From Eq. (23) and (30) the
physical critical wavenumber at the time of matter and radiation
equality is given by
.
The physical setting could be two large volumes of cold dark matter
colliding or some non-homogeneous velocity flows in the early
universe. In the first case the contact surface would be prone to the
Kelvin-Helmholtz instability and in the second the instability would
occur inside the flow.
From Eq. (23) and (30) the
physical critical wavenumber at the time of matter and radiation
equality is given by
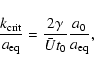 |
(32) |
| (33) |
A significant feature of this example is that the instability occurs at such a small scale. This is important because it is well known that the cold dark matter model has problems at small scales. It seems to predict higher densities and more small scale structure than is observed. Modifications of the CDM have been tried, e.g. Warm Dark Matter and Self-Interacting Dark Matter but neither of these solves all the problems, see e.g. (Primack 2002; Tasitsiomi 2002) for an outline of the ideas and detailed references. While these discrepancies may be, at least partially, due to numerical and observational resolution and selection effects or the consequences of baryonic physics, there still appears to be a residual problem.
The surprising element of the Kelvin-Helmholtz effect is that it
occurs even on expanding backgrounds and depending on the value of
![]() the instabilities can grow exponentially. Our results
indicate that further analysis using numerical methods is needed
to explore the effect into the nonlinear regime.
the instabilities can grow exponentially. Our results
indicate that further analysis using numerical methods is needed
to explore the effect into the nonlinear regime.
Acknowledgements
The authors would like to thank Anne Green, Andrew Liddle, Roy Maartens, Dominik Schwarz, David Wands and David Weinberg for useful discussions. KM is supported by a Marie Curie Fellowship under the contract number HPMF-CT-2000-00981.