M. Kaasalainen¹ - T. Kwiatkowski² - M. Abe³ - J. Piironen¹ - T. Nakamura⁴ - Y. Ohba³ - B. Dermawan⁵ - T. Farnham⁶ - F. Colas⁷ - S. Lowry⁸ - P. Weissman⁸ - R. J. Whiteley⁹ - D. J. Tholen¹⁰ - S. M. Larson⁹ - M. Yoshikawa³ - I. Toth¹¹ - F. P. Velichko¹²

1 - Observatory, University of Helsinki, PO Box 14, 00014 Helsinki, Finland
2 - Astronomical Observatory, Adam Mickiewicz University, ul. S $\l$ oneczna 36, 60-286 Poznan, Poland
3 - The Institute of Space and Astronautical Science, 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, Japan
4 - National Astronomical Observatory, Mitaka, Tokyo 181-8588, Japan
5 - School of Science, The University of Tokyo, Bynkyo, Tokyo 113-0033, Japan
6 - Department of Astronomy, University of Texas at Austin, Austin, TX 78712, USA
7 - IMCCE, Observatoire de Paris, 77 Av. Denfert Rochereau, 75014 Paris, France
8 - Earth and Space Sciences Division, Jet Propulsion Laboratory, Pasadena, CA 91109, USA
9 - Lunar and Planetary Laboratory, University of Arizona, 1629 E. Univ. Blvd. Tucson, AZ 85721-0092, USA
10 - Institute for Astronomy, Woodlawn Drive, 96822, Honolulu, HI, USA
11 - Konkoly Observatory, Post Office Box 67, Budapest 1525, Hungary
12 - Astronomical Observatory of Kharkiv National University, 35 Sums'ka St., 61022 Kharkiv, Ukraine

Abstract
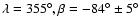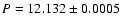We present photometric observations of the near-Earth asteroid (25143) 1998 SF36 from the 2001 apparition campaign, and we discuss the corresponding physical model. The asteroid's photometric behaviour is consistent with an S-type object, it has a retrograde pole at $\lambda=355^\circ, \beta=-84^\circ\pm 5^\circ$ , and its sidereal rotation period is $P=12.132\pm 0.0005$ hours. 1998 SF36 is elongated, with rough global dimension ratios a/b=2.0, b/c=1.3, but the elongation is not due to a bifurcated shape. The surface is not likely to contain major concavities. No significant albedo variegation was detected.

Key words: solar system: minor planets, asteroids - techniques: photometric - methods: numerical

1 Introduction

This paper describes some results of an extensive photometric campaign, lasting from December 2000 till September 2001, during which several observatories collected 53 lightcurves. In Sect. 2 we describe the observations, and the model is presented in Sect. 3. We provide a summary in Sect. 4.

2 Observations

**Table 1:** Details of observations.
Date (2000-2001)	Observatory	Telescope/CCD	Filters	Observers
Dec. 27, 28	Kitt Peak	2.3 m/Steward 21 CCD	R	R. J. Whiteley, S. M. Larson
Jan. 23	Mauna Kea	2.2 m/TEK 2k $\times$ 2k	R	D. J. Tholen, R. J. Whiteley
Jan. 24 ,26	McDonald	2.1 m/SITe 1k $\times$ 1k	V, R	T. L. Farnham
Feb. 2-4	Steward	1.54 m/2k $\times$ 2k CCD	R	S. Lowry, P. Weissman
Feb. 2, 14, 16-17	Bisei Spaceguard	0.25 m/Apogee AP10	V	Yoshikawa et al. (1)
Feb. 15, 18, 19, 22, 25-27	Mitaka	0.5 m/Astromed CCD	B, V, R, I	Nakamura et al. (2)
Feb. 20-22, 25, 26	Pic du Midi	1 m/Thomson 7863	R	T. Kwiatkowski, F. Colas
Feb. 27	Konkoly	1 m/Wright EEV	V, R, I	I. Toth
Mar. 2, 13, 15, 16, 19	Mitaka	0.5 m/Astromed CCD	B, V, R, I	Nakamura et al. (2)
Mar. 21-23	Table Mountain	0.6 m/SITe 1k $\times$ 1k	R	S. Lowry, P. Weissman
Mar. 26, 29, 31	Kiso	1.05 m/SITe 2k $\times$ 2k	R	Abe et al. (3)
Mar. 28, 29, 31	McDonald	2.1 m/SITe 1k $\times$ 1k	V, R	T. L. Farnham
Mar. 31	Kharkiv	0.7 m/SBIG ST-6	R	F. P. Velichko
Apr. 1	McDonald	2.1 m/SITe 1k $\times$ 1k	V, R	T. L. Farnham
Apr. 1	Kiso	1.05 m/SITe 2k $\times$ 2k	R	Abe et al. (3)
Jun. 21, 22	McDonald	2.1 m/SITe 1k $\times$ 1k	V, R	T. L. Farnham
Aug. 22-24	Palomar	1.5 m/2k $\times$ 2k	R	S. Lowry, P. Weissman
Aug. 22-25	Kiso	1.05 m/SITe 2k $\times$ 2k	R	M. Abe et al. (4)
Sep. 23-25	Palomar	1.5 m/2k $\times$ 2k	B, V, R, I	S. Lowry, P. Weissman

(1) M. Yoshikawa, A. Asami, D. J. Asher, T. Fuse, N. Hashimoto, A. I. Ibrahim, S. Isobe, S. Nakano, K. Nishiyama, Y. Oshima,
J. Terazono, H. Umehara, T. Urata.
(2) B. Dermawan, T. Nakamura, H. Fukushima, H. Sato, F. Yoshida, Y. Sato.
(3) M. Abe, Y. Ohba, S. Hasegawa, H. Fukai (4) M. Abe, Y. Ohba, M. Ishiguro, Y. Takagi.

During the observing campaign 1998 SF36 swept a long arc on the sky, making it possible to study it at various viewing/illumination geometries (Fig. 1). A detailed list of photometric observations is presented in Table 1.

The observations split into 2 periods: from 27 Dec. 2000 to 1 Apr. 2001 and from 22 Aug. to 25 Sep. 2001. There are a few lightcurves in between but, mainly because of the small solar elongation of 1998 SF36, they are noisy and cover only a short part of the rotational period.

Because of the large number of collected lightcurves and their incompleteness caused by a rotation period close to 12 hours, we do not present plots of all individual observations. They are available in a uniform computer format and can be provided on request. To show a general picture of the light variations of 1998 SF36, we have selected three of the best composite lightcurves, which are shown in Fig 2. They were obtained with various filters and composited with the rotation period of 12.13 hours. Despite different illumination/viewing geometries, the lightcurve amplitudes were quite similar throughout the whole period of visibility.

3 Model

Asteroid 1998 SF36 was a very faint object for most of the time, so many of the observed lightcurves are very noisy while others have only a few points. In addition to this, several lightcurves turned out to have an unaccountable time shift (probably due to computer clock offset) - we checked that, after a manual time offset correction, the model lightcurve coincided accurately with these observations. 35 lightcurves clearly have a considerably better quality and quantity of data points than the rest, and they cover the available observing geometries very well, so we used them in the inverse problem analysis (for a description of this technique, see Kaasalainen et al. 2001, 2002 and references therein).

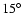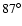The solar phase angle varied between $15^\circ$ and $87^\circ$ for the observations; this gives us a rough idea of the target's phase curve even though a detailed study is not possible due to the lack of small phase angles crucial for estimating the light-scattering characteristics (Kaasalainen et al. 2003). In Fig. 3 we show the rudimentary phase curve points for 1998 SF36. As in Kaasalainen et al. (2001), these were corrected to equatorial viewing geometry using the adopted pole and shape model below. This was done by defining a scale factor for each observed lightcurve by dividing the mean brightness intensity of the observed points by that of the model points. The reference phase curve can then be plotted by viewing the model from the equatorial direction at the corresponding solar phase angles, and multiplying the mean of such a model lightcurve by the respective scale factor. For this plot, we used only those well-observed curves that were reported as absolute photometry. 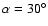In spite of this, the data of two lightcurves near $\alpha=30^\circ$ were clearly not well calibrated. R-points were fitted with an exponential-linear function (Kaasalainen et al. 2001), while calibrated V-points are currently too scarce for a meaningful fit; we estimate (V-R)=0.55 mag. The magnitudes are given in the standard reduction distance 1 AU from both the Earth and the Sun. The observed phase behaviour is consistent with an S-type object (see, e.g., Helfenstein & Veverka 1989).

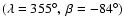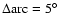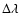A retrograde pole solution $(\lambda=355^\circ,~\beta=-84^\circ)$ (J2000) with $\Delta{\rm arc}=5^\circ$ was clearly superior to other possibilities. The error estimate is given in degrees of arc since there is no sense in giving $\Delta\lambda$ for a pole this close to the South ecliptic pole. Another solution on the other side of the ecliptic pole would have had as good a chi-square, but the resulting shape would have been in an unphysical rotational state. No indication of significant albedo variegation was detected.

Composite lightcurves from various nearby nights enabled us to estimate current synodical periods of rotation, and thus get an initial trial interval for the sidereal period; we found this interval to be [12.115, 12.135] hours. The sidereal rotation period had a distinct best solution 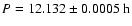$P=12.132\pm 0.0005~ {\rm h}$ within this interval (and no matching ones were found within an even larger check interval).

The pole geometry means that illumination was always almost equatorial, and most views were of the upper half of the asteroid (i.e., the southern half from ecliptic viewpoint). The lower half was not seen as well, but both asteroid pole regions were visible (August-September 2001 curves were crucial for this). The rough dimension ratios of the shape are a/b=2.0, b/c=1.3. The available observations do not cover potential observing geometries densely, so the shape model, shown in Fig. 4, cannot be constrained very strongly; nevertheless, the existing lightcurve details do not allow large deviations from the portrayed global shape. This model is also consistent with radar observations (Ostro et al. 2001). As usual, a combination of the Lommel-Seeliger and Lambert scattering laws and various realistic combinations of Hapke parameters all give quite similar pole and shape results. Model fits for lightcurves well representing different geometries of the 2001 apparition are shown in Fig. 5.

We compared the above results with an independent result from the Epoch-Amplitude (EA) method (Kwiatkowski 1995). The latter, though more an estimate than a solution to an inverse problem, provides a good consistency check. We found the two results to be totally consistent: the EA pole was only a few degrees different ( 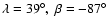$\lambda=39^\circ,~\beta=-87^\circ$ ; there was also the unrealistic solution on the other side of the South pole), and the sidereal rotation period was the same. The ellipsoid axis ratios were also very similar (a/b=1.9, b/c=1.2).

$\begin{figure} \par\includegraphics[width=4.1cm,clip]{Fe052_f5a.eps}\hspace*{4mm... ...}\hspace*{4mm} \includegraphics[width=4.1cm,clip]{Fe052_f5i.eps} \end{figure}$

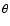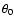Figure 5: Selected lightcurves (asterisks) and the corresponding fits (dashed lines) for 1998 SF36. The horizontal axes give the rotational phase in degrees, and the vertical axes brightness in units of relative intensity. The viewing latitude (measured from the pole) is given by $\theta$ , and the illumination latitude by $\theta _0$ . The solar phase angle is given by 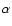$\alpha$ .

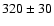In Ishiguro et al. (2003), an absolute size estimation was carried out using the visible-wavelength photometric data and near-middle infrared data. The estimated effective diameter of 1998 SF36 was found to be about $320 \pm 30$ m, very roughly translating into maximal extents of (550 m, 270 m, 210 m) for our model. Colorimetric analysis was also performed in Dermawan et al. (2002). The above papers corroborate S-type taxonomic classification (with somewhat higher albedo than for typical S-class asteroids). Ohba et al. (2003) found a pole solution similar to ours and concluded that the role played by the surface roughness can have an effect on the inferred relative shape dimensions such as the degree of the flattening of the body. As discussed in Torppa et al. (2003), tight constraints for these dimensions require numerous accurate observations with absolute photometry (and may even then remain ambiguous due to the scattering law), so they are probably better obtained with complementary data.

4 Discussion

The surface of the asteroid does not seem to have extreme concavities since the lightcurves at high solar phase angles show no particular features. As shown in Durech & Kaasalainen (2003), this means that the nonconvexities on the surface must be smaller than, e.g., those on 433 Eros. However, the high-phase curves do not cover a complete rotation densely (probably due to the diurnal resonance of the asteroid's rotation period), so the effect of some topographic features particularly on the lower half of the asteroid may have remained unseen.

The combined analysis of photometric data with other data sources should provide more insight into the properties of this near-Earth asteroid, and the results from the MUSES-C mission in 2005 will add one more valuable case to the few "ground truth'' targets at our disposal, particularly after the inclusion of the data from the 2004 apparition of 1998 SF36.

Contents

CCD photometry and model of MUSES-C target (25143) 1998 SF36

1 Introduction

2 Observations

3 Model

4 Discussion

References