| (1) | |||
| (2) | |||
| (3) |
A&A 405, 387-396 (2003)
DOI: 10.1051/0004-6361:20030415
J. G. L. Rae 1 - N. J. B. Green2 - T. W. Hartquist1 - M. J. Pilling3 - T. Toniazzo1,4
1 - Department of Physics and Astronomy, University of Leeds, Leeds
LS2 9JT, UK
2 - Chemistry Department, Kings College London, London
WC2R 2LS, UK
3 - School of Chemistry, University of Leeds, Leeds
LS2 9JT, UK
4 - Met. Office, London Road, Bracknell, Berkshire,
RG12 2SZ, UK
Received 6 November 2002 / Accepted 12 March 2003
Abstract
A model of the grain surface chemistry involving the accretion of
atoms of two different elements, X and Y, and their reactions to form
species X2, XY, and Y2 was examined for a wide range of choices
for the values of its three free parameters - the accretion rate of X
and Y, the desorption rate of X and the grain surface sweeping time
of Y, all considered relative to the grain surface sweeping rate of X.
Relative production rates of the diatomics were calculated with five
methods involving, respectively, a high-order truncation of the master
equation, a low-order truncation of the master equation, the standard
deterministic rate equation approach, a modified rate equation
approach and a set of approximations which are in some cases
appropriate for accretion dominated chemistry.
The accuracies of the relative production rates calculated with the
different methods were assessed for the wide range of model parameters.
The more accurate of the low-truncation master equation calculations
and the standard deterministic rate equation approach gives results
which are in most cases within ten or twenty per cent of the results
given by the high-truncation master equation calculations.
For many cases, the more accurate of the low order truncation and the
standard deterministic rate equation approaches is indicated by a
consideration of the average number of atoms of the two species on the
grain's surface.
Key words: astrochemistry - molecular processes - ISM: clouds - dust, extinction - ISM: molecules
If species accrete from the gas phase onto the surfaces of grains more quickly than they diffuse across a grain surface and react with each other, the surface chemistry is said to be taking place in the reaction limit. Such chemistry has been treated by Pickles & Williams (1977), who used a system of rate equations similar to those employed in gas-phase chemistry. This approach is often referred to as the standard deterministic rate equation method.
In some cases, species diffuse across grain surfaces and react with each other faster than they accrete. Therefore, when a species is accreted, and there is already another reactive species on the grain, they are likely to react before another particle accretes. The rates of reaction are therefore limited by the rates of accretion; the chemistry is said to be occurring in the accretion limit. Under these conditions, the average numbers of reactive species on a grain are small, and a stochastic model is required. The first attempts at stochastic modelling of interstellar grain surface chemistry in the accretion limit were made by Allen & Robinson (1977) and Tielens & Hagen (1982). The model of Allen & Robinson (1977) was constructed under the assumption that when a molecule is produced in a grain surface reaction, it immediately enters the gas phase; the model was extended by Tielens & Hagen (1982) to allow for the accumulation of grain mantles. In their model, Tielens & Hagen (1982) used Monte Carlo techniques to calculate the steady-state concentrations of mantled species. Later, various other authors constructed Monte Carlo models of grain surface chemistry (e.g. Tielens & Allamandola 1987; Tielens 1995 (unpublished); Charnley et al. 1997; Tielens & Charnley 1997; Charnley 2001). Charnley (1998) used Monte Carlo methods to solve the master equation (which gives the probability that there is a certain number of particles of each species) governing gas-phase chemistry, and suggested that a similar approach may be applicable to grain surface chemistry.
As Monte Carlo simulations are computationally too expensive to use in the study of large systems, Caselli et al. (1998, 2002) and Shalabiea et al. (1998) introduced semi-empirical modifications to the standard determininstic rate equations, with the aim of solving the problem of inaccuracy of rate equation methods in the accretion limit.
Biham et al. (2001) and Green et al. (2001) studied, with a master equation approach, the production rate of H2 on surfaces. Green et al. (2001) used a generating function method to obtain an analytic solution for the H2 production rate. They also investigated more complex chemistries, using sparse matrix techniques to obtain the probabilities that a grain contains given numbers of particles of each species. With this approach, the calculation must be truncated at a certain maximum number of particles of each species, i.e. there is some truncation value for the number of particles, above which the probabilities are assumed to be zero. With a high enough truncation value, the results are almost exact. Green et al. (2001) used the probabilities obtained in this way to calculate the rates of production of molecules on grain surfaces. They solved the master equation numerically for the system of H and O, reacting on grain surfaces to form H2, O2, and OH, and also for the system of H, O, and N, reacting to form H2, O2, OH, NH, N2, NO, NO2, H2O, and NH3. They compared the results given by the solution of the master equation with a high truncation value, to those given by (i) the use of the master equation method with a low truncation value; (ii) the standard deterministic rate equation; and (iii) an approximate method, based on the assumption that the sweeping rate of atomic hydrogen on grain surfaces is so great that a reactive species already on the surface of a grain will react as soon as an H atom is accreted.
Stantcheva et al. (2002) solved the master equation for the system of H, O, and CO reacting on the surfaces of grains to produce O2, H2, H2O, CO2, H2CO, and CH3OH. They investigated the accuracy of results given by the method for different truncation values and also the accuracies of results given by other approaches.
In this paper, we examine the system of atoms X and Y reacting to form X2, XY, and Y2 on grain surfaces. We study a wide variety of adsorption, desorption, and diffusion rates, covering the accretion limit, the reaction limit, and cases intermediate between them. We compare the almost exact results, obtained through the solution of the master equation for high truncation values, with the results obtained (i) through the solution of the master equation with low truncation values; (ii) with the approximate method used by Green et al. (2001); (iii) with the standard deterministic rate equation approach; and (iv) with a modified rate equation approach similar to that employed by Caselli et al. (2002). Although the network we study is smaller than that of Stantcheva et al. (2002), we examine a much larger range of adsorption, desorption, and diffusion rates, thereby gaining insight into the parameter ranges in which each method may be applied.
In Sect. 2, the various approaches to the problem are discussed. We present our results in Sect. 3, and Sect. 4 concludes the paper.
We normalise with respect to
![]() as follows.
as follows.
The production rates of X2, XY, and Y2 were calculated with the
various approaches for
![]() sets of values of
sets of values of ![]() ,
,
![]() ,
,
![]() between 0.1 and 10. Calculations were also
performed for
between 0.1 and 10. Calculations were also
performed for
![]() sets of
sets of
![]() ,
,
![]() ,
,
![]() .
.
We now discuss in detail the master equation approach, the standard and modified rate equation approaches, and the approximate method of Green et al. (2001).
Green et al. (2001) gave the master equation for the hydrogen and
oxygen system in their Eq. (29), and the rates of production of H2, OH, and O2 in their Eqs. (26) to (28). The generalisation
of their equations to species X, Y, X2, XY, and Y2 is trivial.
The average numbers of X and Y atoms on the surface of a
grain are:
We introduced modifications to the rate equations, similar to those suggested by Caselli et al. (1998, 2002) in their attempt to develop a set of deterministic equations appropriate in both the reaction limit and the accretion limit. The modifications we used were based on those used by Caselli et al. (2002).
We define
![]() and
and
![]() as
as
In the case that
![]() and
and
![]() ,
the
probability that species Y reacts is either less than or equal to 1,
so that for Y2 formation the standard deterministic rate equation
approach
can be used. However the probability that species X reacts is greater
than 1, and the equations for the production of X2 and XY must
be modified. The rate coefficients
,
the
probability that species Y reacts is either less than or equal to 1,
so that for Y2 formation the standard deterministic rate equation
approach
can be used. However the probability that species X reacts is greater
than 1, and the equations for the production of X2 and XY must
be modified. The rate coefficients
![]() and
and
![]() are replaced by
the larger of
are replaced by
the larger of ![]() and
and ![]() (Caselli et al. 1998, 2002); this
quantity will be denoted by
(Caselli et al. 1998, 2002); this
quantity will be denoted by
![]() .
In addition, the formation rate
of X2 is multiplied by the probability that X reacts with another X
instead of with a Y, and the rate of formation of XY is multiplied by
the probability that X reacts with Y and not with another X
(following Caselli et al. 2002). The production rates,
.
In addition, the formation rate
of X2 is multiplied by the probability that X reacts with another X
instead of with a Y, and the rate of formation of XY is multiplied by
the probability that X reacts with Y and not with another X
(following Caselli et al. 2002). The production rates,
![]() (X2) and
(X2) and ![]() (XY), of X2 and XY, in this approach become
(XY), of X2 and XY, in this approach become
The case in which
![]() and
and
![]() is the same
as the previous case, except that X is replaced by Y and vice versa.
So
is the same
as the previous case, except that X is replaced by Y and vice versa.
So ![]() (X2) can be calculated with the standard determistic rate
equation approach, and the rates of formation,
(X2) can be calculated with the standard determistic rate
equation approach, and the rates of formation, ![]() (XY) and
(XY) and ![]() (Y2), of XY and Y2, are
(Y2), of XY and Y2, are
In the case in which both
![]() and
and
![]() are greater than 1, the rate equations for X2, XY, and Y2 must be modified.
For the formation rates of X2 and Y2 we used Eqs. (15) and (18), respectively. For the XY formation rate, we used Eq. (16) when
are greater than 1, the rate equations for X2, XY, and Y2 must be modified.
For the formation rates of X2 and Y2 we used Eqs. (15) and (18), respectively. For the XY formation rate, we used Eq. (16) when
![]() ,
and Eq. (17) when
,
and Eq. (17) when
![]() .
.
In all cases, the rates of change of
![]() and
and
![]() are
are
Green et al. (2001) introduced an analytic approximation to the
master equation method, based on the assumption that the sweeping rate
of X is so fast that if there is a reactive species (X or Y in this
case) on the surface of a grain, a X atom accreting onto the grain
will react immediately. This is equivalent to assuming that
![]() ,
and that the probability of there
being more than one reactive species on the surface of a grain is
small. Green et al. (2001) showed that, under
these assumptions
,
and that the probability of there
being more than one reactive species on the surface of a grain is
small. Green et al. (2001) showed that, under
these assumptions
![\begin{displaymath}P (0,0) \approx \left[ \frac{3}{2} + \frac{\alpha}{2\alpha + \delta} \right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2003/26/aah4090/img66.gif) |
(24) |
Following Caselli et al. (1998), we calculated the relative abundances of X2, XY, and Y2 on the surfaces of grains as
Figures 1 to 4 show the magnitudes of the percentage discrepancies between: the results given by the standard rate equation approach, and the exact results (Fig. 1); the results given by the modified rate equation approach, and the exact results (Fig. 2); the results given by the approximate method, and the exact results (Fig. 3); and the results given by the master equation approach for the low truncation case, and the exact results (Fig. 4).
Due to lack of space, the results are plotted against ![]() and
and ![]() for
for ![]() only. Results for other values of
only. Results for other values of ![]() can
be found at http://ast.leeds.ac.uk/~jglr.
In each of Figs. 1 to 4, plot (a) shows the
discrepancies in x(X2); plot (b)
shows the discrepancies in x(XY); and plot (c) shows
the discrepancies in x(Y2).
can
be found at http://ast.leeds.ac.uk/~jglr.
In each of Figs. 1 to 4, plot (a) shows the
discrepancies in x(X2); plot (b)
shows the discrepancies in x(XY); and plot (c) shows
the discrepancies in x(Y2).
In Fig. 5, the percentage discrepancies are plotted
against
![]() and
and
![]() ,
the average numbers of X and Y
atoms on the surface of a grain, as given by the exact method and
Eqs. (11) and (12).
The white gaps at the top left-hand and bottom left-hand corners of
the plots in Fig. 5 are caused by the fact that we did
not explore regions of
,
the average numbers of X and Y
atoms on the surface of a grain, as given by the exact method and
Eqs. (11) and (12).
The white gaps at the top left-hand and bottom left-hand corners of
the plots in Fig. 5 are caused by the fact that we did
not explore regions of ![]() -
-![]() -
-![]() space that yielded
these values of
space that yielded
these values of
![]() and
and
![]() .
The uneven contours
in Fig. 5 are caused by the fact that any point in
.
The uneven contours
in Fig. 5 are caused by the fact that any point in
![]() -
-
![]() space does not correspond to a single point in
space does not correspond to a single point in ![]() -
-![]() -
-![]() space, and therefore the discrepancies do
not depend only on
space, and therefore the discrepancies do
not depend only on
![]() and
and
![]() .
In Fig. 6 the discrepancies are
plotted against
.
In Fig. 6 the discrepancies are
plotted against
![]() and
and
![]() for
for ![]() only. Again
the white areas are regions of
only. Again
the white areas are regions of
![]() -
-
![]() space to which
no point in
space to which
no point in ![]() -
-![]() space corresponds for
space corresponds for ![]() .
In
Figs. 5 and 6, plots a, b and c are for the standard rate equation approach, plots d, e, and f for the modified rate equation approach, plots g, h, and i
for the approximate method, and plots j, k, and l for the low-truncation case of the master equation
approach. Plots a, d, g,
and j give the percentage discrepancy in x(X2), plots b, e,
h, and k the percentage discrepancy in x(XY), and plots c,
f, i, and l the percentage discrepancy in x(Y2). In
Figs. 5 and 6, the ranges of
.
In
Figs. 5 and 6, plots a, b and c are for the standard rate equation approach, plots d, e, and f for the modified rate equation approach, plots g, h, and i
for the approximate method, and plots j, k, and l for the low-truncation case of the master equation
approach. Plots a, d, g,
and j give the percentage discrepancy in x(X2), plots b, e,
h, and k the percentage discrepancy in x(XY), and plots c,
f, i, and l the percentage discrepancy in x(Y2). In
Figs. 5 and 6, the ranges of
![]() -
-
![]() are different because there is no desorption of Y, so X and Y are not
symmetric.
are different because there is no desorption of Y, so X and Y are not
symmetric.
In all of Figs. 1 to 6, lighter regions indicate lower percentage discrepancies, and darker regions higher percentage discrepancies.
Although only the results for ![]() are shown in Fig. 1, it was found that the results given by the
rate equation approach are inaccurate for the case of low
are shown in Fig. 1, it was found that the results given by the
rate equation approach are inaccurate for the case of low ![]() ,
high
,
high ![]() ,
and low
,
and low ![]() ,
corresponding to situations in which the rates of
accretion are low and the rates of X desorption, and
of reactions (2) and (3), are high,
so that the average surface population on a grain is low. This
conclusion is confirmed by Figs. 5a-c and 6a-c, which show that this approach is least accurate
for small
,
corresponding to situations in which the rates of
accretion are low and the rates of X desorption, and
of reactions (2) and (3), are high,
so that the average surface population on a grain is low. This
conclusion is confirmed by Figs. 5a-c and 6a-c, which show that this approach is least accurate
for small
![]() and
and
![]() .
These are the conditions under which it is
known that the rate equation approach breaks down.
.
These are the conditions under which it is
known that the rate equation approach breaks down.
The inaccuracies in the results given by the modified rate equation
approach are shown in Fig. 2 for ![]() ,
and in Figs. 5d-f and 6d-f. In most cases these
results are no more accurate than those of the standard rate equation
approach, and sometimes the accuracy is much less.
Stantcheva et al. (2002) studied the system of H and O reacting on
the surfaces of grains to form H2, OH, and O2, and gave in their Figs. 1 to 3 results for the
values of x(H2), x(OH), and x(O2) calculated by various
different methods including the modified rate equation approach and
the master equation method. The modified rate equation approach they
used was the same as that used by Stantcheva et al. (2001), which was
based on that used by Caselli et al. (1998).
They found good agreement between results
obtained with these
two approaches for the parameters they considered, which were mostly
rather different from those used by us.
They used the same values for
,
and in Figs. 5d-f and 6d-f. In most cases these
results are no more accurate than those of the standard rate equation
approach, and sometimes the accuracy is much less.
Stantcheva et al. (2002) studied the system of H and O reacting on
the surfaces of grains to form H2, OH, and O2, and gave in their Figs. 1 to 3 results for the
values of x(H2), x(OH), and x(O2) calculated by various
different methods including the modified rate equation approach and
the master equation method. The modified rate equation approach they
used was the same as that used by Stantcheva et al. (2001), which was
based on that used by Caselli et al. (1998).
They found good agreement between results
obtained with these
two approaches for the parameters they considered, which were mostly
rather different from those used by us.
They used the same values for ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() as
Hasegawa et al. (1992), Caselli et al. (1998),
and Green et al. (2001). The accretion rate they used for oxygen was different
from that used for hydrogen. Their parameters were equivalent to
as
Hasegawa et al. (1992), Caselli et al. (1998),
and Green et al. (2001). The accretion rate they used for oxygen was different
from that used for hydrogen. Their parameters were equivalent to
![]() ;
;
![]() ;
;
![]() ;
and
;
and
![]() .
This corresponds to a region below and to the left of that
shown in the plots in
Fig. 2, and for a higher value of
.
This corresponds to a region below and to the left of that
shown in the plots in
Fig. 2, and for a higher value of ![]() .
It can be seen that towards the bottom left-hand corner of
Fig. 2a, the results are more accurate than elsewhere, which is
consistent with the findings of Stantcheva et al. (2002).
.
It can be seen that towards the bottom left-hand corner of
Fig. 2a, the results are more accurate than elsewhere, which is
consistent with the findings of Stantcheva et al. (2002).
Figure 3 shows that the approximate method gives inaccurate
results for x(X2) when ![]() is high.
If the desorption rate is high, the assumption that an X atom will
always react if it accretes onto a grain that is already populated is
invalid. It was also found that
there are inaccuracies in the values calculated for x(Y2) for high
is high.
If the desorption rate is high, the assumption that an X atom will
always react if it accretes onto a grain that is already populated is
invalid. It was also found that
there are inaccuracies in the values calculated for x(Y2) for high ![]() ,
for all values of
,
for all values of ![]() .
In these cases, the accretion
rate is comparable to, or greater than, the rate of reaction of Y,
and the population of grains containing several Y atoms is non-negligible.
At high values of
.
In these cases, the accretion
rate is comparable to, or greater than, the rate of reaction of Y,
and the population of grains containing several Y atoms is non-negligible.
At high values of ![]() ,
the results were found to be
inaccurate for a wide range
of values of
,
the results were found to be
inaccurate for a wide range
of values of ![]() and
and ![]() ,
particularly for x(X2) and x(Y2); x(XY) is only inaccurate for high
,
particularly for x(X2) and x(Y2); x(XY) is only inaccurate for high ![]() and low
and low ![]() .
The approximate
equations were constructed under the assumption that if there are two atoms of species Y on the surface of a grain, and a third accretes,
Y2 will not be formed. If we instead assume that a grain surface
containing no atoms of X and more than two atoms of Y will always be a
site of Y2 formation, Eq. (23) should be replaced with
.
The approximate
equations were constructed under the assumption that if there are two atoms of species Y on the surface of a grain, and a third accretes,
Y2 will not be formed. If we instead assume that a grain surface
containing no atoms of X and more than two atoms of Y will always be a
site of Y2 formation, Eq. (23) should be replaced with
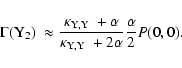 |
(28) |
Figure 4 shows that the inaccuracy in the results given by the
master equation method with low truncation
values is high for high ![]() .
In particular,
the inaccuracy was found to be high in the
case of high
.
In particular,
the inaccuracy was found to be high in the
case of high ![]() ,
low
,
low ![]() ,
and low
,
and low ![]() .
This corresponds to the case
of a high rate of accretion, a low rate of X desorption, and
high rates for reactions (2) and (3). This is the
case in which there is a large population of X atoms on the surfaces
of the grains. The inaccuracy is also high for high
.
This corresponds to the case
of a high rate of accretion, a low rate of X desorption, and
high rates for reactions (2) and (3). This is the
case in which there is a large population of X atoms on the surfaces
of the grains. The inaccuracy is also high for high ![]() ,
high
,
high ![]() ,
and high
,
and high ![]() ,
which corresponds to fast rates of
accretion and X desorption, and a slow rate for reaction (3).
This results in a large population
of Y atoms on the surfaces of the grains. The results given by the
master equation method with low truncation values are therefore
inaccurate when there are large numbers of atoms on the surfaces of
grains, as should be expected; this can also be seen in Figs. 5j-l and 6j-l.
,
which corresponds to fast rates of
accretion and X desorption, and a slow rate for reaction (3).
This results in a large population
of Y atoms on the surfaces of the grains. The results given by the
master equation method with low truncation values are therefore
inaccurate when there are large numbers of atoms on the surfaces of
grains, as should be expected; this can also be seen in Figs. 5j-l and 6j-l.
Figure 7 shows the regions of
![]() -
-
![]() space
in which the standard rate equation approach, or the low-truncation
master equation approach, is more accurate. Plot a is for X2,
plot b
for XY, and plot c for Y2. Dark regions indicate that
the rate equation approach is more accurate; light regions are those
in which the low-truncation master equation approach is more reliable.
Regions of intermediate
shading indicate that both approaches give results which are accurate
to within 10%. As expected, when either the results given by one
method or both methods are not accurate to within 10%, the
low-truncation master equation approach is more accurate at low values
of
space
in which the standard rate equation approach, or the low-truncation
master equation approach, is more accurate. Plot a is for X2,
plot b
for XY, and plot c for Y2. Dark regions indicate that
the rate equation approach is more accurate; light regions are those
in which the low-truncation master equation approach is more reliable.
Regions of intermediate
shading indicate that both approaches give results which are accurate
to within 10%. As expected, when either the results given by one
method or both methods are not accurate to within 10%, the
low-truncation master equation approach is more accurate at low values
of
![]() and
and
![]() ,
and the rate equation approch at higher
values. The better of the two approaches gives results for x(X2), x(XY), and x(Y2) which are usually within 10 or 20% - and always within 25% - of those given by the exact method, except for the results given for x(Y2)
in a small region of
,
and the rate equation approch at higher
values. The better of the two approaches gives results for x(X2), x(XY), and x(Y2) which are usually within 10 or 20% - and always within 25% - of those given by the exact method, except for the results given for x(Y2)
in a small region of ![]() -
-![]() -
-![]() space around
space around
![]() ,
,
![]() ,
,
![]() .
In these cases, the
more accurate method is the rate equation approach, and the value of x(Y2) given by that method is around 40% less than the exact value.
.
In these cases, the
more accurate method is the rate equation approach, and the value of x(Y2) given by that method is around 40% less than the exact value.
Although in general the rate equation approach is more accurate than
the low-truncation master equation approach for higher values of
![]() and
and
![]() ,
it can be seen in Fig. 7 that
for
,
it can be seen in Fig. 7 that
for
![]() ,
,
![]() ,
the low-truncation master
equation approach is more accurate for X2. However, in most of
these cases the results given by the two methods are very similar, and
the discrepancies between them and the exact results are within about 20%.
,
the low-truncation master
equation approach is more accurate for X2. However, in most of
these cases the results given by the two methods are very similar, and
the discrepancies between them and the exact results are within about 20%.
We have studied grain surface chemistry with a variety of approaches with a range of parameters. We deliberatelty made our study as general as was reasonable given the amount of work involved in a multiparameter study. We did so in anticipation of revisions of rates pertaining to specific problems treated in earlier literature, and of future studies of surface astrochemistry in a very wide range of environments including some in which atomic hydrogen accretion is unimportant.
The modified rate equation method was found to be no more
accurate than the standard rate equation approach under the conditions
examined; indeed it was in many cases less accurate. The modified
rate equation method that we used is closely related to that of
Caselli et al. (2002). They studied a system in which reaction
barriers are important, and the values of ![]() approriate for
their studies are large. The modified rate equation approach that we
used gives reliable results for large
approriate for
their studies are large. The modified rate equation approach that we
used gives reliable results for large ![]() for some values of
for some values of ![]() .
Hence, our findings are in harmony with those of Caselli et al. (2002). The modified rate equation approach that we adopted
differs from that employed by Stantcheva et al. (2001) which they
found to give reliable results for the specific
.
Hence, our findings are in harmony with those of Caselli et al. (2002). The modified rate equation approach that we adopted
differs from that employed by Stantcheva et al. (2001) which they
found to give reliable results for the specific
![]() and
large
and
large ![]() cases they examined. They, like the authors of a number
of papers referenced here, were examining a region of parameter space
they thought to be relevant when hydrogen accretion is important for
the surface chemistry and the surface reactions proceed without
barriers. Of the approximate methods we have examined, only the
low-order truncated master equation approach is reliable for general
small
cases they examined. They, like the authors of a number
of papers referenced here, were examining a region of parameter space
they thought to be relevant when hydrogen accretion is important for
the surface chemistry and the surface reactions proceed without
barriers. Of the approximate methods we have examined, only the
low-order truncated master equation approach is reliable for general
small ![]() ,
large
,
large ![]() cases.
cases.
The approximate method of Green et al. (2001), which was devised specifically for the H, O system, was also found to give inaccurate results under certain conditions, but can be improved by considering the possibility that an atom of species Y may accrete onto the surface of a grain on which there are already two Y atoms.
The standard rate equation approach was found to work well except under conditions which lead to there being a small average number of X and Y atoms on the surface of a grain. Under these conditions, the master equation approach with low truncation values is accurate. Therefore, a combination of the two approaches should be enough for a reasonably accurate calculation of the X2, XY, and Y2 abundances in the parameter regime we considered - generally within about 20% of the exact values. Practical approaches to the use of stochastic models are under investigation (Stantcheva et al. 2001).
Acknowledgements
JGLR was supported by grants from the Leverhulme Trust and PPARC. TT was supported by a grant from PPARC.