Astronomical Institute, Academy of Sciences of the Czech Republic, 251 65 Ondrejov, Czech Republic

Abstract
An analysis of the long-term X-ray activity of the ultra-compact binary 4U 1820-30 within the years 1996-2002, using the ASM/RXTE data, is presented. The X-ray light curve displays complicated large-amplitude variations, even on short time scales of a few days. Episodes of brief low states (BLS), lasting for several days, are superposed on the general course of the cycle, the length of which we determined to be $T_{\rm C}=172.780$ days by the method of the O-C residuals. We found no significant secular trend in $T_{\rm C}$ ; this is consistent with the stable period found over longer time intervals by Chou & Grindlay (2001) and is thus consistent with the triple model. The statistical distribution of 1.5-12 keV intensity, $I_{\rm sum}$ , for all data is not far from Gaussian although some deviations exist. The $I_{\rm sum}$ curve, folded with the 172 day cycle and smoothed, shows a rapid rise, double-peaked maximum, and a slow decline. The course of the smoothed residuals of this curve, the so called $\sigma _{\rm res}$ curve, is more complicated than the $I_{\rm sum}$ curve, with several minima and maxima. Two sharp maxima of $\sigma _{\rm res}$ coincide with the rising branch and the dip after the maximum of the $I_{\rm sum}$ curve. We have shown that the scatter of the folded $I_{\rm sum}$ curve is dominated by the BLS. The activity is discussed in terms of several models. Thermal instability of the disk can be excluded. The increases of the mass transfer from the donor star are likely to explain the 172 day cycle of activity. However, we argue that the highly asymmetric X-ray light curve of this cycle, with the long and complicated profile of the decay branch, cannot be explained purely by the influence of a third body via the Mazeh & Shaham (1979) mechanism. Instead, a hybrid model in which the irradiation-driven instability of the donor star governs the complicated profile of the decay with the superposed BLS appears to be more viable.

Key words: stars: neutron - stars: binaries: close - stars: circumstellar matter - stars: individual: 4U 1820-30

4U 1820-30 is a strong and persistent X-ray source, located in the globular cluster NGC 6624. Its orbital period of just 685 s ( $\approx$ 11 min) is one of the shortest among known cosmic binaries (Stella et al. 1987a).

The evolutionary model (Rappaport et al. 1987) speaks in favour of a partly degenerate He-rich donor star, transferring matter onto a neutron star. There remains a problem with the observed sign of the secular changes of the orbital period which is opposite to the predicted one, but this difference may be explained by the attracting force of the globular cluster (Chou & Grindlay 2001).

The long-term variations of the X-ray intensity of 4U 1820-30 appear to be cyclic with the cycle-length of about 176 days originally estimated by Priedhorsky & Terrell (1984). The most comprehensive long-term timing analysis was conducted by Chou & Grindlay (2001). The X-ray spectrum of 4U 1820-30 has been subject to a number of analyses, the most recent and comprehensive one being that by Bloser et al. (2000). They found that the track of 4U 1820-30 in the color-color diagram during the 171 day cycle is consistent with an atoll source. This suggests that the cycle is a manifestation of mass-transfer variations, and not a precessing disk. This finding is in accordance with the occurrence of X-ray bursts. They are observed only when 4U 1820-30 is near the state of the minimum X-ray intensity. The X-ray bursts become more frequent as the X-ray intensity rises and then they disappear completely (Stella et al. 1984).

The recent monitoring of 4U 1820-30 by ASM/RXTE enabled us to obtain a very dense and almost continuous coverage within 1996-2002. About 13 cycles have been covered. This data set is very suitable for the analysis of the time-averaged properties of the long-term activity of this unique object.

2 Sources of the data

The recent activity of 4U 1820-30 within the years 1996-2002 was observed by the All Sky Monitor (ASM) onboard Rossi X-ray Timing Explorer (RXTE) (http://xte.mit.edu/). This monitor provides long-term observations of an unprecedented quality for this object. The data file contained the sum band intensities $I_{\rm sum}$ (1.5-12 keV) and the hardness ratios $HR1= I_{\rm B}(3{-}5~{\rm keV})/I_{\rm A}(1.5{-}3~{\rm keV})$ , $HR2= I_{\rm C}(5{-}12~{\rm keV})/I_{\rm B}(3{-}5~{\rm keV})$ . Only one-day means (1693) were used in order to increase the signal/noise ratio. This binning is sufficient because our analysis concentrates on the long-term activity of 4U 1820-30 and hence on features in the light curve on the time scale of days and longer. Modified Julian Date, used by RXTE, was transformed into more often used Julian Date. Hereafter it is used in the form of JD - 2 400 000.

$\begin{figure} \par\includegraphics[angle=-180,width=14cm,clip]{2694f1.ps} \end{figure}$

Figure 1: The X-ray light curve of 4U 1820-30 over the years 1996-2002 according to the ASM/RXTE observations. One-day means of the sum band (1.5-12 keV) intensity are shown. They are connected by the lines for the densely covered intervals. The uncertainties quoted in the original file of RXTE measurements are marked. The triangles above and below the curve denote the moments of maxima and minima, respectively (Sect. 3.2). The fit by the moving averages for Q=17 days is also shown. The vertical bars mark the positions of the prominent and well covered episodes of brief low states, analyzed in detail in Sect. 3.2.2. See Sect. 3.1 for details. (This figure is available in color in electronic form at http://www.edpsciences.org)

3 Data analysis

3.1 General description

The whole sum band ASM/RXTE X-ray light curve, covering the years 1996-2002, is shown in Fig. 1. The points are connected by the lines for the densely covered intervals to guide the eye and to resolve the rapid variations. $I_{\rm sum}$ varies between about 5 and 35 ct/s. This curve represents about 13 cycles of the length reported by Priedhorsky & Terrell (1984) and Chou & Grindlay (2001). The course of the variations is complicated, although the basic pattern of the $\approx$ 170 day cycle can be resolved. The error bars which represent the quoted uncertainty are marked. It can be seen that the data often display appreciable fluctuations, even on short time scales of a few days. The X-ray orbital modulation was reported to be quite small, of the order of 3 percent (Stella et al. 1987a). This suggests that the complicated variations in Fig. 1 are not caused by the orbital modulation. Episodes of brief low states, hereafter referred to as BLS and described in detail in Sect. 3.2.2, are superposed on the general course of the $\approx$ 170 day cycle (mostly on its decay branch).

In order to show clearly the smooth profile of the variations through the $\approx$ 170 day cycle, the X-ray light curve was fitted by the two-sided moving averages with the filter half-width Q=17 days and a step of one day. Q refers to the semi-interval within which the data were averaged. Q=17 days was chosen after several trials; it yields the fit which satisfies the general course of the observed curve but, at the same time, it averages through most BLSs.

The statistical distribution of $I_{\rm sum}$ for all observed data from Fig. 1 is displayed in Fig. 2a. It is not far from being Gaussian although some deviations exist. The top of the histogram is flatter than the Gaussian. There is also an asymmetry between the left-hand and the right-hand side. The slope of the right-hand side appears steeper than that of the left-hand side and falls below the Gaussian curve for $I_{\rm sum}>31$ ct/s. The high and low levels of intensity of the $\approx$ 170 day cycle are just barely resolvable in the histogram for the individual measurements of $I_{\rm sum}$ in Fig. 2a. This means that there are no peaks near the high and low limits. The statistical distribution for the fit from Fig. 1 displays a somewhat different pattern (Fig. 2b). It is broader than the Gaussian curve for $11<I_{\rm sum}<27$ ct/s and more narrow outside this interval. This suggests that the histogram in Fig. 2a is dominated by the rapid fluctuations and BLS while Fig. 2b better reflects the properties of the $\approx$ 170 day cycle.

3.2 The cycle-length

The determination of the cycle-length in the ASM/RXTE data set was carried out by the method of the O-C residuals. It makes use of the residuals from some reference period and enables us to determine $T_{\rm C}$ and to analyze its variations. This method is not sensitive to the exact length of the reference period and allows us to check the position of each measured feature on the O-C diagram at each epoch.

Three features in the X-ray light curve allowed us a reasonably accurate timing: the moment of the maximum intensity, $T_{\rm max}$ ; the moment of the minimum intensity, $T_{\rm min}$ , and the moment when the intensity is crossing $I_{\rm sum}=20$ ct/s on the rising branch of the cycle. $T_{\rm max}$ and $T_{\rm min}$ were determined by fitting a polynomial. The timings could be determined for all the consecutive events and are marked in Fig. 1.

The O-C curves were constructed for all three features. The fluctuations of O-C were small in comparison with the length of $T_{\rm C}$ . There is no prominent secular trend in the O-C curve of any feature. The value of $T_{\rm C}=172.780$ days was determined from the linear fit to the O-C curve of the rising branch of the cycle. This feature displayed the smallest scatter of the O-C's - the standard deviation of $T_{\rm C}$ , determined from the O-C's, is 10 days and is caused by the intrinsic cycle-to-cycle fluctuations of the profile of the $I_{\rm sum}$ curve. We therefore used this value of $T_{\rm C}$ for the further analysis. The ephemeris for the maxima of intensity which will be used in the next sections was derived:

$\begin{figure} \par\includegraphics[angle=-180,width=8.8cm,clip]{2694f2.ps} \end{figure}$

Figure 2: The statistical distribution of $I_{\rm sum}$ of 4U 1820-30. The histograms for the observed data and for the fit from Fig. 1 are displayed in a) and b), respectively. The binning of 1 ct/s was used. The Gaussian curves are plotted for comparison. See Sect. 3.1 for details.

$\begin{figure} \par\includegraphics[angle=180,width=8.6cm,clip]{2694f3.ps} \end{figure}$

Figure 3: a) The X-ray sum band light curve of 4U 1820-30 folded with the 172 day cycle of activity. The phases were calculated according to the ephemeris in Eq. (1). The ASM/RXTE measurements within the years 1996-2002 are displayed. The folded data were smoothed by the two-sided moving averages for the filter half-widths Q=0.05, 0.06, 0.08, 0.10, and 0.12 phase (see the legend in b)). b) Smoothed residuals $\sigma _{\rm res}$ of the fits. c) Smoothed skewness of the residuals. d) The number of observations included in the calculation of each mean. See Sect. 3.2.1 for details. (This figure is available in color in electronic form.)

3.2.1 Properties of the folded curve

The 172 day cycle repeats accurately enough to enable an analysis of the properties of the folded $I_{\rm sum}$ curve. All data were therefore folded according to Eq. (1). The resulting curve is shown in Fig. 3a. The profile with a steep rise and slower decline can readily be resolved. The scatter is substantial, especially at some phases. In order to determine the mean course of $I_{\rm sum}$ , the folded data were smoothed by the two-sided moving averages. Several values of Q were used. These fits are superposed in Fig. 3a; it can readily be seen that they rapidly converge to a common and well determined smooth curve with the decrease of Q. Further decrease of Q does not add any details, hence the fits shown here can be taken as the representative of the course of the folded $I_{\rm sum}$ curve. The smoothed curve shows especially these features: (a) rapid rise within phases 0.75-1.0; (b) a depression just after the maximum; (c) slow, roughly linear decline within phases 0.16-0.6.

The residuals of the fit to $I_{\rm sum}$ were smoothed by the moving averages again. This yielded the $\sigma _{\rm res}$ curve, shown in Fig. 3b. The $\sigma _{\rm res}$ curve is a measure of the degree to which the intensity curve in a given phase reproduces for the respective epochs. Notice that the $\sigma _{\rm res}$ curve is more complicated than the $I_{\rm sum}$ curve. A broad minimum at phase $\approx$ 0.7 coincides with the minimum of the intensity curve. The global maximum of the $\sigma _{\rm res}$ curve occurs at phase 0.15 and coincides with the shallow depression which follows the maximum of the intensity curve. The second highest peak in the $\sigma _{\rm res}$ curve at phase 0.85 coincides with the middle of the rising branch of the $I_{\rm sum}$ curve.

Figure 3c shows the smoothed course of the skewness $\gamma_1$ of the residuals of the smoothed $I_{\rm sum}$ curve. $\gamma_1=0$ corresponds to the symmetric distribution of the residuals. $\gamma_1<0$ and $\gamma_1>0$ correspond to the asymmetric distributions with a tail towards more negative or positive values, respectively. It can easily be seen from Fig. 3c that vast majority of phases possess $\gamma_1<0$ . Notice that the minimum of the $\gamma_1$ curve corresponds to the maximum of the $I_{\rm sum}$ curve.

3.2.2 Brief low states

The X-ray light curve of 4U 1820-30 is quite complicated, with rapid variations on the time scale of a few days, superposed on the 172 day cycle. Even some brief fadings from the maximum down to the minimum level of $I_{\rm sum}$ (with an amplitude of $\approx$ 20 ct/s) with the decay branch lasting about 10 days can be resolved. An inspection of the curves revealed that $I_{\rm sum}$ often recovers back to the previous level after the fading. These fadings and subsequent rises were abbreviated as BLS in Sect. 3.1.

The light curves of the respective BLSs were examined. It emerged that there appears to be some maximum rate of decline even for the smoothest decay branches. A test of the working hypothesis that this slope remains the same for the individual events was therefore made for the BLSs with relatively smooth decays, using the method of matching a template. The mean rate of decline 1.85 ct/s/day was determined.

The match of the rising branches of the BLSs was less certain. An examination of the profiles revealed that the course of the rise generally displays larger rapid fluctuations than the decline. The rising branch profile sometimes shows faster risetimes near the maximum.

3.3 X-ray color behaviour

The X-ray color behaviour during the 172 day cycle was analyzed using the HR1's and HR2's. All the available HR1's and HR2's were plotted versus $I_{\rm sum}$ . Both curves were found to contain several points which displayed quite large errors in HR's. In order to lower the noise, we carried out the following procedure. Firstly, all points which had the quoted uncertainty of their HR's $\sigma_{\rm q}\geq0.3$ were rejected. Secondly, in order to resolve the mean course of the HR1 and HR2 curves, they were fitted as a function of $I_{\rm sum}$ by the code HEC13, written by Dr. P. Harmanec and based on the method of Vondrák (1969 and 1977). This code can fit a smooth curve to the data no matter what their course is. The fits with the parameters $\epsilon=1$ , $\Delta I_{\rm sum} = 4.5$ ct/s were proven to satisfy the data. Finally, 5 percent of the most negative and 5 percent of the most positive residuals of the fit were rejected; a new fit with the same parameters as before was then repeated for the remaining data. This fit was truncated at $I_{\rm sum}=31$ ct/s because the amounts of data were too low to enable a reliable fit above this limit.

It is obvious from Fig. 4a that a monotonic function for HR1 was obtained. A very slight wave at the upper part of the curve is not considered to be significant. On the other hand, the course of HR2 is more complicated (Fig. 4b). HR2 reaches a minimum at $I_{\rm sum}\approx14$ ct/s and increases toward both larger and smaller $I_{\rm sum}$ 's.

It is also important to analyze the color changes during the BLS. The reason is that the amplitude of $I_{\rm sum}$ of some BLSs is comparable to the full range of variations during the 172 day cycle. It is therefore important to know if the color changes during BLS are consistent with the mean course of variations of all data. The following well covered segments were used for the three BLS: JD 2 450 322-JD 2 450 353 (decay and rise); JD 2 451 837-JD 2 451 866 (minimum and rise); JD 2 452 000-JD 2 452 026 (decay and beginning of rise). The arithmetic means for the intervals of $I_{\rm sum}$ 5 ct/s were calculated instead of fitting because of a small amount of data for the BLS. We can conclude that the course of the color changes during the BLS is consistent with the mean profile of the color variations of the whole data set (Fig. 4).

$\begin{figure} \par\includegraphics[angle=-180,width=8.8cm,clip]{2694f4.ps} \end{figure}$

Figure 4: The dependence of HR1 and HR2 on $I_{\rm sum}$ in 4U 1820-30. The scales of the axes are identical for both diagrams. The thick smooth lines represent the fits by the code HEC13 to the whole data set. The large empty circles represent the arithmetic means just for three episodes of deep BLS, calculated for the intervals of $I_{\rm sum}$ 5 ct/s. The data of the BLS are marked by the dark (blue) points. See Sect. 3.3 for details. (This figure is available in color in electronic form.)

The 3D X-ray color-color diagram, displayed in Fig. 5, was constructed from the fits to the data in Fig. 4. This plot enables us to analyze the spectral changes in the softer X-ray passband than that used by Bloser et al. (2000) and to compare our results with theirs. Notice that the banana-like track can be resolved even in the 1.5-12 keV band. The determination of the color-color track from the fits to the HR versus $I_{\rm sum}$ tracks thus appears to be a viable approach how to determine meaningful tracks even from the data in relatively closely spaced channels and suffering from a higher noise.

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{2694f5.eps} \par\end{figure}$

Figure 5: The 3D X-ray color-color diagram for 4U 1820-30. Notice the atoll track in the HR1-HR2 plane. For clarity, the symbols and numbers denote the corresponding values of $I_{\rm sum}$ in ct/s. See Sect. 3.3 for details. (This figure is available in color in electronic form.)

The dependence of both HR1 and HR2 on the phase of the 172 day cycle was examined by the moving averages with Q=0.05 and 0.08 phase (Fig. 6). Both ratios display a clear dependence on the phase, with the profiles resembling the $I_{\rm sum}$ curve from Fig. 3a. The amplitude of the HR1 curve is larger than that of HR2. HR1 displays a small dip at phase 0.2 while this feature is absent in HR2. All this behaviour is in accordance with the profiles in Fig. 4 where the dependence of HR1 on $I_{\rm sum}$ is monotonic while two values of $I_{\rm sum}$ can correspond to a given HR2. However, we note that the part between phases 0.8 and 1.0 in Fig. 6 may be distorted. The scatter caused by the cycle-to-cycle variations of the $I_{\rm sum}$ curve in this phase range leads to a large scatter of the hardness ratios for a given $I_{\rm sum}$ . The fit that averages through this phase region then may not accurately reproduce the steep, rapidly changing profile of the HR's.

The HR versus $I_{\rm sum}$ profiles were also analyzed separately for the rising and decay branches of the 172 day cycle. The fits by HEC13 did not reveal significant differences between the branches. We only note that the loop which is prominent in the bottom part of the fit to the whole data set in Fig. 4b is clearly defined just for the decay branch. However, this can be explained by the large asymmetry of the X-ray light curve (Fig. 3a) which yields a much larger amount of data on the decay branch than on the rising branch and hence allows a much more reliable fit for the decays.

$\begin{figure} \par\includegraphics[angle=-90,width=15.3cm,clip]{2694f6.ps} \end{figure}$

Figure 6: HR1 and HR2 of 4U 1820-30 folded with the 172 day cycle of activity and smoothed by the two-sided moving averages for Q=0.05 and 0.08 phase. The phases were calculated according to Eq. (1). We note that the part between phases 0.8 and 1.0 may be distorted because of the steeply changing profile. See Sect. 3.3 for details. (This figure is available in color in electronic form.)

4 Discussion

We have carried out an analysis of the long-term X-ray activity of the ultra-compact binary 4U 1820-30 within 1996-2002, using the ASM/RXTE data. Complicated large-amplitude variations, even on short time scales of a few days, with episodes of BLSs that are superposed on the general course of the long cycle, were clearly resolved. We determined the length of this cycle $T_{\rm C}=172.780$ days by the method of the O-C residuals. This value is consistent with that obtained by Fourier transformation by Chou & Grindlay (2001). The O-C method has also shown that the mean cycle-length is stable, without any secular trend. The rising branch of the cycle appears to be the most stable part of the cycle. Bloser et al. (2000) have shown that the 172 day cycle is due to the mass-transfer variations onto the neutron star. The good stability of this cycle implies that the injection of matter from the donor, discussed below, repeats accurately.

Stella et al. (1987b) determined the luminosity at the minimum of the 172 day cycle $L_{X_{\rm min}}\approx 2\times10^{37}$ ergs s^-1 for the 1-30 keV passband from the EXOSAT observations. The ASM intensity of 4U 1820-30 at the minimum of the X-ray light curve differs just a little for the individual epochs. We can then make a plausible assumption that the above-mentioned value of $L_{\rm X_{\rm min}}$ can be representative also of the minima observed by ASM/RXTE. The mass transfer rate onto the neutron star, $\dot m$ , can be determined from the accretion luminosity, L_X, through $\dot m=L_{X} R_{\rm NS}/(\eta G M_{\rm NS})$ , where $M_{\rm NS}$ and $R_{\rm NS}$ are the mass and radius of the neutron star, respectively. $\eta$ refers to the efficiency with which the potential energy is converted to radiation. We then obtain $\dot m_{\rm min}\approx 1.7\times10^{-9}~M_{\odot}$ yr^-1 for $L_{X_{\rm min}}\approx 2\times10^{37}$ ergs s^-1 and $\eta\approx1$ , assuming a 1.4 $M_{\odot}$ and 10 km radius neutron star.

The mass transfer rate, $\dot m_{\rm GR}$ , driven purely by the gravitational radiation, can be determined from Eq. (1) of King et al. (200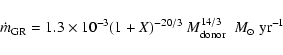2):

Thermal instability of the accretion disk is quite unlikely to be the cause of the 172 day cycle and the BLS. The radius of the disk in 4U 1820-30 is $4.22\times10^{9}$ cm if we assume $R_{\rm disk}=0.7~R_{\rm lobe}$ . Applying the models for He, C, and O disks by Menou et al. (2002), we always obtain $\dot m_{\rm crit}$ , below which the thermal instability can occur, several times lower than $\dot m_{\rm min}$ , even for the extreme values of $R_{\rm disk}=0.9~R_{\rm lobe}$ and of the viscosity parameter $\alpha=1$ . Moreover, the disk is strongly irradiated by the neutron star in 4U 1820-30, which further suppresses the instability.

The variations of the mass outflow from the donor, $\dot m_{\rm donor}$ , appear to be the most plausible explanation for the 172 day cycle. Two promising triggering mechanisms can be assumed. (a) The tidal influence of a more distant third body via the Mazeh & Shaham (1979) mechanism (Chou & Grindlay 2001). (b) The irradiation-induced instability (IDI) of the donor, invoked by the irradiation of the donor by the neutron star and the disk corona.

The highly asymmetric profile of the X-ray light curve of the 172 day cycle (Fig. 3a) suggests a highly non-sinusoidal course of changes of $\dot m$ . A rather symmetric burst of $\dot m_{\rm donor}$ is expected in the case of the Mazeh & Shaham (1979) mechanism. In this mechanism, a third body orbiting the binary with period P₃ induces a long-term modulation of the eccentricity of the inner binary with a period $K P_{3}^{2}/P_{\rm orb}$ . Thus for $P_{\rm orb}=11$ min, and the constant $K\approx1$ (dependent on the relative inclination and mass ratio of the third body), the long-term modulation of 172 d implies P₃=1.1 d (Chou & Grindlay 2001). The observed X-ray intensity depends on the mass transfer rate in the inner disk region, $\dot m_{\rm IN}$ . The initial profile of the burst of $\dot m_{\rm donor}$ will be modified by propagating through the disk. The model by Livio & Verbunt (1988) shows that even an abrupt increase of $\dot m_{\rm donor}$ will give rise to a gradual and slower increase of $\dot m_{\rm IN}$ (and hence also $I_{\rm sum}$ ), occurring on the viscous time scale. If we set $\dot m_{\rm IN}\approx 1.7\times10^{-9}~M_{\odot}$ yr^-1, then we can determine the viscous time of the disk to be $t_{\rm vis}\approx8$ and 2 days for $\alpha=0.1$ and 0.5, respectively, making use of Eq. (4) of Esin et al. (2000). The typical observed duration of the rises, about 20 days, is significantly longer than $t_{\rm vis}$ , unless $\alpha\approx0.03$ . In the framework of the model by Bath et al. (1986), this occurs when the profile of the burst is slower than $t_{\rm vis}$ ; $\dot m_{\rm IN}$ is then governed by the changes of $\dot m_{\rm donor}$ . $t_{\rm vis}\approx2{-}8$ days is consistent with the decay time scale of the BLS, but not with the much longer duration of the decay branch of the 172 day cycle. The circularization time of the close pair will be much longer than 172 days (Mazeh & Shaham 1979). This is in accordance with the fact that the minima of the 172 cycle display no secular trend in intensity.

The color behaviour during BLS is consistent with that of the whole data set (Fig. 4) - this suggests that real large variations of $\dot m_{\rm IN}$ occur during BLS. BLS cannot be invoked by the action of the third body via the mechanism by Bailyn (1987). The reason is that BLSs occur irregularly, on time scales significantly longer than the time scales appropriate for 4U 1820-30 (which would be on the order of the orbital period of the third body $\approx$ 1.1 day, suggested by Chou & Grindlay 2001). All these lines of evidence suggest that even in the framework of the triple star model the decay branch of the X-ray light curve must be prolonged and modulated by additional mechanism(s), possibly by a superposed IDI in a hybrid model, as outlined below.

The irradiative flux on the surface of the donor is $F_{\rm irr}~\propto L_{\rm X}/a^{2}$ . It is then obvious that the donor in 4U 1820-30 will be very strongly irradiated because of its very small $a\approx1.32\times10^{10}$ cm. The IDI will be influenced by the variable shielding of the donor by the disk outer rim; the latitudes up to about 20 $^{\circ}$ can be shielded during the maximum of $I_{\rm sum}$ . The irradiated parts can be heated up to about 10⁵ K (Arons & King 1993). There are several models for IDI (e.g. Hameury et al. 1986; Gontikakis & Hameury 1993; Wu et al. 1995). They agree that in some cases a hysteresis curve for $\dot m_{\rm donor}$ versus the lobe-filling factor is possible. The donor then can switch between high and low $\dot m_{\rm donor}$ . The mean density of the donor in 4U 1820-30 about 3200 g cm^-3 is relatively low for a white dwarf; this star need not be highly degenerate, with a degenerate core and a non-degenerate envelope (Rappaport et al. 1987). This outer layer may be able to react to the outer irradiative flux by expansion. Currently, there is no model of the response of such a kind of star to the irradiation. Following King (1989), we can infer that the conditions in 4U 1820-30 are such that the intense hard X-ray emission from the neutron star is able to reach deep into the outer layer of the donor and that the ratio of the irradiative and intrinsic flux of the donor is high - this speaks in favour of the feasibility of IDI model in 4U 1820-30. The propagation of the burst of $\dot m_{\rm donor}$ in IDI through the disk will be similar to that described above. Although the highly asymmetric profile of the X-ray light curve of the 172 day cycle may be attributed to a long-lasting burst of $\dot m_{\rm donor}$ , comparable to the duration of the decay branch (the course of $\dot m_{\rm IN}$ is governed by the decay of $\dot m_{\rm donor}$ in this case (Bath et al. 1986)), the complicated course of the BLS needs a superposition of an additional mechanism.

Alternatively, a hybrid model, in which the influence of the third body triggers a burst of $\dot m_{\rm donor}$ , can be offered. IDI can then be superposed on the changes invoked by the third body and solve the problem of the long and complicated profile of the decay branch of the 172 day cycle. In this respect, the BLS, or sometimes just a shallow depression, which often appears on the top of the X-ray light curve and whose depth is highly variable for the individual epochs (Fig. 3b) deserves a special attention. We offer a possible scenario for its formation in which IDI plays a role. The height of the outer rim is expected to vary by more than 1/3 during the 172 day cycle because of variable $\dot m_{\rm donor}$ . Due to a large increase of the inflowing matter during the burst of $\dot m_{\rm donor}$ , the vertical thickness of the disk, z₀, increases. The shielding of the L₁ point therefore increases - this in turn leads to a temporary decrease of $\dot m_{\rm donor}$ and hence to a decrease of $\dot m_{\rm IN}$ on $t_{\rm vis}$ . The corresponding decrease of z₀ and consequent increase of irradiation of the donor again lead to an additional mass outflow from the donor. The time scale of this process will also be controlled by the delay caused by the time needed to transport the heat from the higher latitudes of the donor to the vicinity of the L₁ point.

In the light of the above-mentioned lines of evidence, we argue that the complicated profile of the 172 cycle is governed by a superposition of several mechanisms. The course of $\gamma_1$ with the phase of the cycle, with the prevailing $\gamma_1<0$ (Fig. 3c), suggests that the BLSs dominate the course of the X-ray intensity curve during the cycle. Both the profile and the rate of decline of these BLSs remain quite similar for the respective events with relatively smooth curves. The smaller slope of the more complicated declines can be interpreted by the superposed rapid (day-to-day) fluctuations. The rises from the BLSs are more complicated but some events are symmetric with the rate of decline very similar to that of the rise. This suggests that the rises are controlled by $t_{\rm vis}$ in a similar way as the decays, as argued above. Also the X-ray color variations are helpful in the identification of the underlying mechanism. They display the atoll track in the 1.5-12 keV band during the 172 day cycle (Fig. 5). The atoll track in 4U 1820-30 was previously resolved over a wider passband (2-16 keV) by Bloser et al. (2000). Here we have shown that such a track can be resolved also in the softer and more narrow passband. Figure 5 shows that both HR1 and HR2 increase for most of the length of the track. Bloser's et al. (2000) data reveal that their hard color decreaseswhile their soft color increases for most of the length of the track. These differences may be interpreted as due to (in part) the relative differences in the sensitivities of the ASM vs. the PCA for the bands chosen. We also resolved the color behaviour during the BLS (Fig. 4) (no episode of a deep BLS was covered by the observations by Bloser et al. 2000). The color changes during BLS are consistent with those of the whole data set. This suggests that real large variations of $\dot m_{\rm IN}$ occur during BLS and that the variations of the disk- magnetosphere boundary (see Bloser et al. 2000) are the same as during the 172 day cycle. The long time scale of the BLS, on the order of several days, is comparable to $t_{\rm vis}$ and is much longer than the orbital time of the disk. Also the amplitude of some BLSs is very high, even comparable to the full range of $I_{\rm sum}$ during the whole 172 day cycle. All this suggests that the whole disk is involved in BLS. Real variations of $\dot m_{\rm donor}$ , modified by the viscous processes in the disk, appear to be the most promising explanation.

Contents

Long-term X-ray activity of the ultra-compact binary 4U 1820-30

1 Introduction