Contents

• New Period-Luminosity and Period-Color relations of classical Cepheids: I. Cepheids in the Galaxy
• 1 Introduction
• 2 The color data for Galactic Cepheids
• 3 Comparison of the P-C and C-C relation for the Galaxy, LMC and SMC
• 4 Absolute magnitude data for Galactic Cepheids from Feast and Gieren et al.
• 5 Absorption-to-reddening ratios in B, V, and I for Cepheids
• 6 The Galactic P-L relations
• 7 The instability strip for the Galaxy, LMC, and SMC in the HR diagram
• 8 Cepheids as extragalactic distance indicators
• 9 Conclusions
• References

A&A 404, 423-448 (2003)
DOI: 10.1051/0004-6361:20030354

New Period-Luminosity and Period-Color relations of classical Cepheids: I. Cepheids in the Galaxy

G. A. Tammann¹ - A. Sandage² - B. Reindl¹

1 - Astronomisches Institut der Universität Basel, Venusstrasse 7, 4102 Binningen, Switzerland
2 - The Observatories of the Carnegie Institution of Washington, 813 Santa Barbara Street, Pasadena, CA 91101, USA

Received 24 December 2002 / Accepted 5 March 2003

Abstract
321 Galactic fundamental-mode Cepheids with good B, V, and (in most cases) I photometry by Berdnikov et al. (2000) and with homogenized color excesses E(B-V) based on Fernie et al. (1995) are used to determine their period-color (P-C) relation in the range $0.4<\log P\la1.6$. The agreement with colors from different model calculations is good to poor. - Distances of 25 Cepheids in open clusters and associations (Feast 1999) and of 28 Cepheids with Baade-Becker-Wesselink (BBW) distances (Gieren et al. 1998) are used in a first step to determine the absorption coefficients ${\cal R}_{B}=4.17$, ${\cal R}_{V}=3.17$, and ${\cal R}_{I}=1.89$ appropriate for Cepheids of intermediate color. The two sets of Galactic Cepheids with known distances define two independent P-L relations which agree very well in slope; their zero points agree to within $0\hbox{$.\!\!^{\rm m}$ }12\pm0\hbox{$.\!\!^{\rm m}$ }04$. They are therefore combined into a single mean Galactic P-L_B,V,I relation. The analysis of HIPPARCOS parallaxes by Groenewegen & Oudmaijer (2000) gives absolute magnitudes which are brighter by $0\hbox{$.\!\!^{\rm m}$ }21\pm0\hbox{$.\!\!^{\rm m}$ }11$ in V and $0\hbox{$.\!\!^{\rm m}$ }18\pm0\hbox{$.\!\!^{\rm m}$ }12$ in I at $\log P=0.85$. Agreement with P-L relations from different model calculations for the case [Fe/H] = 0 is impressive to poor.

Galactic Cepheids are redder in (B-V)⁰ than those in LMC and SMC as shown by the over 1000 Cloud Cepheids with good standard B, V, I photometry by Udalski et al. (1999b,c); the effect is less pronounced in (V-I)⁰. Also the (B-V)⁰, (V-I)⁰ two-color diagrams differ between Cepheids in the Galaxy and the Clouds, attributed both to the effects of metallicity differences on the spectral energy distributions of the Cepheids and to a shift in the effective temperature of the middle of the instability strip for LMC and SMC relative to the Galaxy by about $\Delta \log T_{\rm e}\sim 0.02$ at $M_{V}=-4\hbox{$.\!\!^{\rm m}$ }0$, hotter for both LMC and SMC. Differences in the period-color relations between the Galaxy and the Clouds show that there cannot be a universal P-L relation from galaxy-to-galaxy in any given color.

The inferred non-uniqueness of the slope of the P-L relations in the Galaxy, LMC, and SMC is born out by the observations. The Cloud Cepheids follow a shallower overall slope of the P-L relations in B, V, and I than the Galactic ones. LMC and SMC Cepheids are brighter in V than in the Galaxy by up to $0\hbox{$.\!\!^{\rm m}$ }5$ at short periods ( $\log P = 0.4$) and fainter at long periods ( $\log P \ga 1.4$). The latter effect is enhanced by a suggestive break of the P-L relation of LMC and SMC at $\log P = 1.0$ towards still shallower values as shown in a forthcoming paper.

Key words: Cepheids - Magellanic Clouds - distance scale - supernovae: general - cosmological parameters

1 Introduction

This is the first paper of a projected three paper series. The purpose of Paper I here is to begin a new analysis of the properties of classical fundamental-mode Cepheid variables, their two-color, period-color (P-C), and period-luminosity (P-L) relations in the Galaxy. We also give a preliminary comparison of these relations with their counterparts in the LMC and SMC.

The goal of the series is to provide a prelude to a projected final summary paper of our calibration of the absolute magnitudes of type Ia supernovae from the Cepheid distances to their parent galaxies (Sandage et al. 1992; Saha et al. 2001 for the first and last of eleven papers in that series; Parodi et al. 2000 for an interim summary), as these data relate to the value of the Hubble constant.

To maintain consistency throughout the supernovae calibration project that began in 1992, we provisionally adopted the same period-luminosity relation for Cepheids that had been proposed by Madore & Freedman (1991) and used by them in their HST Cepheid program for their new calibration of the Tully-Fisher relation. They assumed that the slope of the P-L relation was universal and was given by the Cepheids in the LMC. They also adopted a zero point based on their assumed LMC distance modulus of  (m - M)⁰ = 18.50.

However, to make a new "finer analysis'' in our projected summary paper that is to come, we necessarily must start with a new discussion of the Cepheid period-luminosity relation itself, its slope, its zero point, and whether the relation is the same from galaxy-to-galaxy. The purpose of this paper and the two that will follow is to begin such a rediscussion of the Cepheid relations.

The question of galaxy-to-galaxy variations of the colors of Cepheids, based on photoelectric observations, was pioneered by Gascoigne & Kron (1965) who found SMC Cepheids to be bluer than Galactic ones. Gascoigne (1974) was also the first to discuss the metallicity effect on Cepheid luminosities. Here we address anew the Cepheid period-luminosity relation centered on the question if that relation is the same from galaxy-to-galaxy. Such an inquiry of uniqueness was beyond adequate solution until recently; the observational data on colors and absolute magnitudes by independent means was too meager for both the Galaxy and other external galaxies.

This has now changed because of four new comprehensive photometric studies of Cepheids in the Galaxy, in the two Magellanic Clouds, and in IC 1613. For the Galaxy, Berdnikov et al. (2000) have published homogeneous B, V, I photometry on the Cape (Cousins) photometric system (as realized by Landolt 1983, 1992) for hundreds of Galactic Cepheids for which Fernie (1994) and Fernie et al. (1995) have determined the E(B-V) color excesses.

The calibration of absolute magnitudes for the Galactic Cepheids has also an excellent new prospect using the 53 Cepheids for which Feast & Walker (1987), updated by Feast (1999), together with Gieren et al. (1998) have determined absolute magnitudes by two independent methods (main sequence fittings in clusters and associations, and the Baade-Becker-Wesselink [BBW] method), with good agreement between them.

In other galaxies, Udalski et al. (1999b,c, 2001) have published photoelectric B, V, I magnitudes, also on the Cape (Cousins) system, for well over 1000 Cepheids in LMC, SMC, and IC 1613, as well as individual values of E(B-V) determined from adjacent red-clump stars.

In the present paper we compare the color and absolute magnitude data for the Galaxy, the LMC and the SMC. The object is to test for either agreement or discrepancies in the slopes of the P-L relations, and in the color-color and period-color relations.

The plan in this paper for the Galactic Cepheids is manifold. In Sect. 2.1 the apparent mean B, V, I magnitudes as published by Berdnikov et al. (2000) for 324 Galactic Cepheids are listed in Table 1. These magnitudes were reduced by these authors from their own observations and from additional sources as listed in the original paper. Known overtone pulsators were excluded. Also listed are the E(B-V) color excess values based on nine studies from the literature as reduced to Fernie's reddening system in Sect. 2.2. This "Fernie system'' is then subjected to additional tests, and a small systematic correction is developed by a new procedure in Sect. 2.3. The same procedure is used in Sect. 2.4 to obtain "corrected'' E(V-I)color excesses.

The new reddening results are applied to the data in Table 1, resulting in a system of adopted reddening-free intrinsic (B-V)⁰ and (V-I)⁰ colors, also listed in Table 1. The period-color and color-color relations using these Galactic data are compared in Sect. 3.1 with those in the LMC and SMC. These comparisons all show systematic differences. To this point no absolute magnitude data have been needed.

Preliminary absolute magnitudes are introduced in Sect. 4 (Tables 3 and 4) from the independent calibrations of Feast (1999) and Gieren et al. (1998). These are required before discussion of a definitive P-L relation can be made because we must calculate new values of the absorption-to-reddening ratios required for the Cepheids. These, of course, differ from the standard ratios that apply for the bluer O,B, and A supergiants because of the effect of color differences on the values due to the wide band widths of broad-band photometric systems. The exact absorption-to-reddening ratios are important for the Galactic Cepheids because their median reddening is large at $<\!E(B-V)\!>~ = 0.58$, requiring that the large absorption corrections calculated with the ratios must be very accurate. Section 5 sets out how we have redetermined these absorption ratios in B, V, and I using distances from Feast and Gieren et al. from Sect. 4, and then iterated to calculate definitive ${{\cal R}_{B,V,I}}$ ratios valid for individual Cepheids depending on their individual colors.

With this preparation, we begin in Sect. 6.1 the discussion of the P-L relation using the calibrating data from Feast (1999) and Gieren et al. (1998). The independent P-L relations from cluster fittings and from the BBW method agree well, and are combined to produce our finally adopted Galactic P-L relations in B, V, and I of Eqs. (15), (16), and (17) and Fig. 11.

These data are then compared with the independently determined slopes of the P-L relations of 650 absorption-corrected Cepheids in LMC and 405 equally treated Cepheids in SMC from Udalski et al. (1999b,c), with its zero-point determined by adopting the distance modulus of the LMC using many methods that are independent of the Cepheids. The slopes (at $\log P = 1.0$) differ between the Galaxy, the LMC, and the SMC. This, and the differences in the two-color (B-V vs. V-I) relations between the same galaxies are the main conclusions of the paper.

In Sect. 6.4 we try to make these differences disappear. We test if errors in the adopted reddenings or in the adopted ratios of absorption-to-reddening could cause the observed slope differences in the P-L relation, and in the zero-points of the period-color relations. We fail, and conclude therefrom that the differences are real if the results of Feast (1999) and Gieren et al. (1998) themselves are without systematic error.

In Sect. 7 we discuss the position of the instability strip in the HR diagram for the Galaxy and the LMC, showing again major differences. Changes in the ridge line of the strip in temperature at the blue (faint) end are proposed to explain the difference in the slopes of the P-L relations between the Galaxy and LMC. The general consequences of using Cepheids as distance indicators, in view of these apparent galaxy-to-galaxy differences, are discussed in the final section.

In view of the seriousness of these results, we set out in the following sections the tedious detail for the methods we have used.

   
2 The color data for Galactic Cepheids

   
2.1 The basic data

The photometric data in B, V, and I as published by Berdnikov et al. (2000) are listed in Table 1 for Galactic fundamental-mode Cepheids with periods larger than $\log P = 0.4$. Only confirmed classical, fundamental-mode Cepheids (designated by DCEP by the authors) are accepted. The listed photoelectric magnitudes are intensity means taken over the light curves. The data in B and V are available for 321 Cepheids. Of these, 250 also have intensity-reduced I magnitudes on the Cape-Cousins-Landolt system. (It is to be noted that this system differs substantially from the Johnson I photometric system, Sandage 1997.) The Cepheids listed in Table 1 have been selected such that they also have E(B-V) color excesses from Fernie (1990), as updated by Fernie et al. (1995).

The data in Cols. 2-5 in Table 1 are directly from Berdnikov et al. (2000). The color excesses in Col. 6 are on the Fernie system as averaged from nine independent literature sources as calculated in the next section. The notation ${E(B-V)_{{\rm FS}}}$ denotes the color excess on "Fernie's system'' determined in this way. We show in Sect. 2.3 that these values are too large by a small systematic scale error (Eq. (2) later). Corrected values of ${E(B-V)_{{\rm corr}}}$ and the corresponding ${E(V-I)_{\rm corr}}$ are shown in Cols. 7 and 8. The resulting intrinsic (B-V)⁰ and (V-I)⁰ colors are in Cols. 9 and 10.

   
2.2 Color excesses E (B - V) on the Fernie system

The selected sample of 321 Cepheids has a median color excess of E(B-V)=0.58, whereas Cepheids in external galaxies are preferentially detected if they suffer little extinction in their parent galaxies. Therefore, if one wants to compare Galactic and extragalactic Cepheids, and particularly if one wants to derive extragalactic distances, optimal extinction corrections are of paramount importance. Every effort should be made to apply reliable extinction corrections particularly to the Galactic Cepheids.

The largest body of E(B-V) values of Galactic Cepheids has been derived by Fernie (1990, 1994) which are compiled together with the data of 15 other authors in Fernie et al. (1995). Nine of these external sources with more than 10 entries have mean random deviations from Fernie's extinctions of $\le$ $0\hbox{$.\!\!^{\rm m}$ }07$, but they show (small) systematic deviations which can be well expressed by a linear relation of the form

$$% E(B-V)_{i} - E(B-V)_{\rm Fernie} = a_i E(B-V)_{i} + b_i.$$ (1)

The coefficients a_i and b_i are determined by means of the n_iCepheids which source i has in common with Fernie et al. (1995). The resulting values of a_i and b_i are listed in Table 2.

 

 

Table 2: The coefficients a_i and b_i in Eq. (1).

Authors		ai	bi	$\sigma$	n
Laney & Stobie (1993)	LS	-0.090	0.019	0.05	48
Dean et al. (1978)	DWC	-0.012	0.017	0.05	95
Parsons & Bell (1975)	PB	-0.047	-0.012	0.07	158
Turner et al. (1987)	TLE	0.022	-0.002	0.04	26
Dean (1981)	DE	0.041	-0.001	0.02	36
Pel (1978)	PE	0.003	0.010	0.04	84
Eggen (1996)	EG2	0.177	-0.043	0.05	55
Yakimova et al. (1975)	YT	0.047	-0.022	0.05	152
Bersier (1996)	BERS	-0.033	-0.003	0.04	24

It is remarkable that the mean zero point of the nine sources in Table 2 agrees with the one of Fernie's to within $-0.001\pm0.007$. It seems therefore justified to transform the external sources by means of Eq. (1) into the system of Fernie. The homogenized external E(B-V) for 271 Cepheids - averaged where possible - are compared with the values of Fernie (1990, 1994) in Fig. 1. The scatter in Fig. 1 amounts to $\sigma=0\hbox{$.\!\!^{\rm m}$ }06$. Considering that the E(B-V)s by Parsons & Bell (1975) alone carry a scatter of $\sigma=0\hbox{$.\!\!^{\rm m}$ }07$ into the data, and that four of the homogenized sources deviate from $E(B-V)_{\rm Fernie}$ by $\le$ $0\hbox{$.\!\!^{\rm m}$ }05$ on average, one concludes that the mean error of the color excesses, averaged over all sources, is $\le$ $0\hbox{$.\!\!^{\rm m}$ }03$.

Figure 1: The difference of the mean $E(B-V)_{\rm mean}$ values from nine external sources minus $E(B-V)_{\rm Fernie}$, plotted against $E(B-V)_{\rm mean}$.

The values E(B-V) for 321 Cepheids in Table 1, 271 of which are based on more than one determination, will be referred to as ${E(B-V)_{{\rm FS}}}$ (FS meaning Fernie's system) in the following.

The present procedure of deriving a consistent set of color excesses leaves the possibility that the derived values of  ${E(B-V)_{{\rm FS}}}$ still carry a scale error. A small scale error is indeed detected and is corrected by the procedure in Sect. 2.3 next.

   
2.3 Correction for a systematic trend in ${E(B-V)_{{\rm FS}}}$ to obtain ${E(B-V)_{{\rm corr}}}$

We have made a test for a possible systematic scale error in the Fernie system of the E(B-V) reddening values. We ask if the Fernie reddening system derived in the last section shows systematic trends such as a correlation of color residuals from an adopted period-color relation with ${E(B-V)_{{\rm FS}}}$values. Are the Cepheids with large ${E(B-V)_{{\rm FS}}}$ values systematically redder or bluer in their derived intrinsic colors than Cepheids of the same period with smaller E(B-V) values?

We have made the test by first deriving an interim period-intrinsic color relation from the data in Table 1 by combining the ${E(B-V)_{{\rm FS}}}$reddening values (Col. 6) with the Berdnikov et al. observed apparent B and V magnitudes listed in Cols. 3 and 4 of Table 1. This interim period-color-corrected relation (not shown) of course has an intrinsic scatter (Sandage 1958, 1972) because the lines of constant period in the HR diagram are sloped through the instability strip that has a non-zero color width. Hence, Cepheids will show a range of intrinsic (B-V) colors along that constant period line as it threads through the instability strip with a color width of $\Delta (B-V) = 0\hbox{$.\!\!^{\rm m}$ }26$ (Fig. 15 later).

Suppose that the assumed color excess ${E(B-V)_{{\rm FS}}}$values on the Fernie system were to have a systematic scale error such that large excess values are either too large or too small. The consequence would be that the scatter in the derived intrinsic (but slightly incorrect) color about a mean color-period line would show a correlation with the assumed ${E(B-V)_{{\rm FS}}}$ excess value. This, of course, cannot be physical. It would signal a scale error in the assumed ${E(B-V)_{{\rm FS}}}$ values.

We have made the test, correlating the color residuals about the initial (interim) color-period relation using the Fernie system ${E(B-V)_{{\rm FS}}}$ values. A correlation of these residuals with ${E(B-V)_{{\rm FS}}}$ is shown in Fig. 2, signalling a small scale error in the Fernie system B-Vexcesses. There is a significant correlation of these color residuals with ${E(B-V)_{{\rm FS}}}$. The Cepheids with large ${E(B-V)_{{\rm FS}}}$ excess values are too blue, hence the FS excess values are too large.

Figure 2: The color residuals $\Delta (B-V)$ from the first-step P-C relation in function of the color excess $E(B-V)_{\rm Fernie}$.

This correlation can be removed when the values ${E(B-V)_{{\rm FS}}}$are reduced by a constant scale factor. Figure 2 shows that this factor should be (1-0.047)=0.953. If this factor is applied to the ${E(B-V)_{{\rm FS}}}$ one obtains improved colors, a new P-C relation and new color residuals. The latter show very little dependence on the revised color excesses ${E(B-V)_{{\rm corr}}}$. After a third step, which implies

$$% E(B-V)_{\rm corr} = (0.951\pm0.012)E(B-V)_{\rm FS},$$ (2)

any such dependence is removed. The values ${E(B-V)_{{\rm corr}}}$ are listed in Tables 1, 3 and 4. The corresponding, well defined P-C relation of the 321 Cepheids in Table 1 has the form

$$% (B-V)^0 = (0.366\pm0.015)\log P + (0.361\pm0.013)$$ (3)

and is shown in Fig. 3. - If one had used the uncorrected ${E(B-V)_{{\rm FS}}}$ in the Fernie system the slope would be 0.354 and the Cepheids at $\log P = 1.0$ would be bluer by $0\hbox{$.\!\!^{\rm m}$ }031$.

Figure 3: The adopted Galactic P-C relation in (B-V)0 as obtained from the corrected color excesses ${E(B-V)_{{\rm corr}}}$.

Laney & Stobie (1994) have derived from 47 Galactic Cepheids a slightly steeper slope (0.416), but their color (B-V)⁰ at an intermediate period of $\log P = 1.0$ agrees with Eq. (3) to within $0\hbox{$.\!\!^{\rm m}$ }01$; the latter is redder by $0\hbox{$.\!\!^{\rm m}$ }022$ at $\log P = 0.5$ and bluer by $0\hbox{$.\!\!^{\rm m}$ }028$ at $\log P =1.5$. The good agreement with independent data proves in favor of the adopted zero point of the (B-V)⁰ colors.

The need for a correction to the Fernie system reddenings ${E(B-V)_{{\rm FS}}}$ can more directly be seen simply by dividing the sample into two parts, one using the 100 Cepheids with the smallest reddenings that range between ${E(B-V)_{{\rm FS}}}$ of 0.035 and 0.417 and the 100 Cepheids with the largest Fernie system reddenings that range from 0.750 and 1.764 and comparing the mean color residuals from the preliminary period-color relation in these two groups. This is equivalent to reading the ordinate in Fig. 2 at two mean abscissa points, one for each of the divided groups. Of course this is the same test as made in Fig. 2 by the continuous least squares line calculated using all periods and reddening values.

There is a clear difference in the ordinate of $0\hbox{$.\!\!^{\rm m}$ }027$between these two mean ${E(B-V)_{{\rm FS}}}$ extremes in the divided sample, in the sense that the group with the largest $<\!E(B-V)_{\rm FS}\!>$ is (artificially) bluer. This can only be due to too large a reddening correction on the Fernie system, consistent with Eq. (2).

   
2.4 ${E(V-I)_{\rm corr}}$ values on the corrected reddening system

Observed colors (V-I) follow from Table 1 for 250 Cepheids with known I magnitudes. In a first step it is assumed that $E(V-I) = 1.38 E(B-V)_{\rm corr}$(cf. Schlegel et al. 1998), although this value is not optimized for the colors of Cepheids. Indeed, colors derived on this assumption define a preliminary P-C relation in (V-I), whose residuals still correlate with the adopted E(V-I) (Fig. 4). Repeating the process with $E(V-I) = (1.38 - 0.067) E(B-V)_{\rm corr}$ leads to a considerably weaker dependence of the color residuals on E(V-I), and after two more iterations any such dependence is eliminated, which then requires

$$% E(V-I)_{\rm corr} = (1.283\pm0.011)E(B-V)_{\rm corr}.$$ (4)

If the color excesses ${E(V-I)_{\rm corr}}$ from Eq. (4) are applied to the data in Table 1, one obtains the final P-C relation in (V-I)⁰ (Fig. 5), i.e.

$$% (V-I)^0 = (0.256\pm0.017)\log P + (0.497\pm0.016).$$ (5)

Figure 4: The color residuals $\Delta (V-I)$ from a preliminary P-C relation plotted against the color excess $E(V-I) = 1.38 E(B-V)_{\rm corr}$.

Most of the scatter in Figs. 3 and 4, i.e. $\sigma=0.07$, must be due to the intrinsic width of the instability strip (cf. Sect. 7). This proves in favor of the internal consistency of the color excesses E(B-V) by Fernie et al. (1995), which together with the photometry of Berdnikov et al. (2000) form the basis of Sect. 2.

The P-C relation in (V-I)⁰, derived by Caldwell & Coulson (1986) is slightly steeper (slope 0.292) than Eq. (5). Their (V-I)⁰ colors are redder from $0\hbox{$.\!\!^{\rm m}$ }036$ (at $\log P = 0.5$) to $0\hbox{$.\!\!^{\rm m}$ }060$ (at  $\log P =1.5$).

It should be repeated that Table 1 contains that subset of Cepheids by Berdnikov et al. (2000) which are not suspected to be overtone pulsators or otherwise peculiar. Equations (3) and (5) should therefore reflect the true colors of an (almost) clean sample of fundamental pulsators.

Another point may be remarked here, which will become relevant in Sect. 5 when discussing the absorption coefficients ${\cal R}$. Since

$${\cal R}_V - {\cal R}_I = \frac{E(V-I)}{E(B-V)}$$

one obtains from Eq. (4)

$$% {\cal R}_V - {\cal R}_I = 1.283\pm0.011.$$ (6)

   
3 Comparison of the P-C and C-C relation for the Galaxy, LMC and SMC

   
3.1 The period-color relations

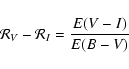
Armed now with the intrinsic period-color relations in Figs. 3 and 5 and their mean (ridge) lines in Eqs. (3) and (5), we compare the P-C relations for the Galactic Cepheids with similar data for the LMC and SMC. That the zero point of these relations differ for the three galaxies is well known (C.D. Laney quoted by Feast 1991; Laney & Stobie 1994). The latter authors ascribed these differences to differences in chemical composition, presumably causing differences in the mean temperature and line blanketing. New comparisons are made in Fig. 6a for (B-V)⁰ and Fig. 6b for (V-I)⁰.

Figure 5: The final Galactic P-C relation in (V-I)0 as obtained from the corrected color excesses ${E(V-I)_{\rm corr}}$.

Figure 6a: The Period-Color relation in (B-V)0 for Cepheids in the Galaxy, LMC, and SMC. The Galaxy data are copied from Fig. 3. The solid line in each panel is the mean relation for the Galaxy from Eq. (3). Three theoretical models by Sandage et al. (1999; SBT), Baraffe & Alibert (2001; BA), and Caputo et al. (2000) are compared with the mean Galaxy line in panel (d). - The paucity of red LMC Cepheids is purely observational due to the few available B magnitudes and saturation effects for $\log P > 1.5$.

Figure 6b: Same as Fig. 6a but for (V-I)0 colors. The Galaxy data are copied from Fig. 5. The Galaxy line in each panel is Eq. (5) of the text.

The LMC relation in a forthcoming paper of this series is based on 650 Cepheids with uniform photometry in the standard B, V, I system and with color excesses which are determined from nearby red-clump stars and which are hence independent of the Cepheid metallicity (Udalski et al. 1999b). The P-C relation of SMC is based on 465 Cepheids whose data are equivalent to those of LMC (Udalski et al. 1999c).

The LMC Cepheids are bluer at all periods by $\sim$ $0\hbox{$.\!\!^{\rm m}$ }09$(depending on period) in (B-V)⁰ than those in the Galaxy. The SMC Cepheids are still somewhat bluer in (B-V)⁰.

The color discrepancies between the Cepheids of individual galaxies are less pronounced in (V-I)⁰. LMC Cepheids are bluer than their Galactic counterparts by $\sim$ $0\hbox{$.\!\!^{\rm m}$ }07$ (depending on period), but the still metal-poorer SMC Cepheids are redder than those in LMC.

The color differences cannot be explained by photometric errors of the required size. They can neither be explained by errors of the color excess corrections because of the contradictory behavior of the P-C relations, i.e. LMC Cepheids are redder in (B-V)⁰, but bluer in (V-I)⁰ than those in SMC. They can also not be due to overtone pulsators which have been carefully eliminated in the present samples.

The conclusion is that the P-C relations of the Galaxy, LMC, and SMC are intrinsically different. If the Cepheids with periods $\log P < 0.4$ had been included here this conclusion would be further supported by SMC whose short-period Cepheids show a break of the P-C relation (cf. Bauer et al. 1999).

The differences between the individual P-C relations leads to the unavoidable conclusion that the Cepheids in the Galaxy, LMC, and SMC cannot follow a unique P-L relation. This point will be taken up again in Sect. 6.

Model calculations of the P-C relations for [Fe/H] = 0.0 by Sandage et al. (1999; based on Geneva models; - in the following SBT), Caputo et al. (2000), and Baraffe & Alibert (2001) are shown in panel (d) of Fig. 6a,b. The Galactic P-C relation in (B-V)⁰ is best matched by the models of SBT and of Baraffe & Alibert (2001), but they are somewhat flat. These authors give also quite similar slopes of the P-C relations in (V-I)⁰ which, however, are flatter than the observed Galactic one. The (V-I)⁰ colors of Baraffe & Alibert (2001) are rather red. The model colors of Caputo et al. (2000) are much too red in (B-V)⁰ and (V-I)⁰.

   
3.2 Comparison of the color-color relations between the Galaxy, LMC, and SMC

A powerful diagnostic for differences in the energy distributions in stellar atmospheres are two-color diagrams. If such differences exist for Cepheids in different galaxies, they can be most easily detected by comparing two-color diagrams, galaxy-to-galaxy.

The comparison of the (B-V)⁰ vs. (V-I)⁰ two-color diagram for the Galaxy, LMC, and SMC are shown in Fig. 7a. The data for the Galaxy are from Table 1. The data for LMC and SMC are from Udalski et al. (1999b,c) corrected for reddening as will be discussed in the Papers II and III for these galaxies.

Figure 7a: Two color-diagrams in (B-V)0 vs. (V-I)0 for Cepheids in the Galaxy, LMC, and SMC in panels a), b), and c). The full line drawn in each panel is the linear least-squares line put through the Galaxy data in panel a). Panel d) shows calculated relations for four values of [Fe/H] from Table 6 of SBT for $\log g = 1.5$ and an atmospheric turbulent velocity of $1.7\nobreak\mbox{$\;$ km~s$^{-1}$ }$. The model lines with the appropriate metallicities are repeated in panels a)- c) as dashed lines.

Predictions of the effect of variable metallicity are in panel (d) taken from the model atmosphere calculations of Bell and Trippico listed in Table 6 of SBT. The nearly vertical lines of constant temperature from these listings can be seen by connecting the discrete plotted points for the temperatures ranging from $5000^{\circ}$ for the reddest points to $6500^{\circ}$ for the bluest, in steps of $500^{\circ}$. The (V-I)⁰ colors at a given temperature are nearly independent of metallicity, whereas (B-V)⁰ colors are not.

The linear fit to the Galaxy data are repeated in all the panels of Fig. 7a. The theoretical lines in panel (d) are curved. They have been superposed on the data in panels (a) to (c) for [Fe/H] values of 0.0, -0.5 and -1.0 respectively from panel (d). The agreement in panel (a) is excellent between the predicted relation for [Fe/H] = 0 and the Galaxy data. Also the LMC and SMC Cepheids in panels (b) and (c) are remarkably well fit by the theoretical lines with the appropriate metallicity. The trends for different metallicities are clear.

Most important are the clear differences between the diagrams for the Galaxy and the two Magellanic Clouds. These differences are real; they cannot be due to errors in the reddening because the reddening vector, shown in panel (a), has very nearly the same slope as the correlation line itself for the well known reason that the law of interstellar reddening of roughly $\lambda^{-1}$ is close to the black-body gradient for temperature reddening. Hence, the differences shown in Fig. 7a between the Cepheids in these three galaxies must be real. Again, similar to the consequences of the differences in Figs. 6a,b, these color differences in Fig. 7a show that even if the P-L relations for the Galaxy and the Clouds were to be identical say in I, they cannot be the same in B or V.

A different presentation of the two-color diagrams is shown in Fig. 7b. Instead of plotting individual Cepheids the mean P-C relations in (B-V)⁰ and (V-I)⁰ are used here. The Galactic P-C relations are given in Eqs. (3) and (5). The preliminary P-C relations of LMC and SMC are taken from Eqs. (23) and (24), respectively (26) and (27), below. The additional information gained here over Fig. 7a are the loci of different periods. These loci are separated by significant amounts in the order of $0\hbox{$.\!\!^{\rm m}$ }1$ in (B-V)⁰ and/or (V-I)⁰. The shift between LMC and SMC is roughly orthogonal to the reddening line, excluding thus errors of the adopted color excesses as a cause. The shift of Cepheids in the two-color diagram proves again that the Cepheids in the Galaxy, LMC, and SMC cannot follow a unique P-L relation.

The strong shifts of the loci of constant period in Fig. 7b cannot be explained by blanketing alone. This conclusion is confirmed by Laney & Stobie (1986) who concluded that SMC Cepheids are hotter than LMC Cepheids by $210\pm80\;$K at constant period, - a conclusion based on their different P-C relations in (J-K) which are little affected by metallicity. We shall return to the question of temperature differences in Sect. 7.3.2, where we require that the differences be a function of absolute magnitude (Eqs. (37)-(39)).

It should be stressed that the adopted P-C relations of LMC and SMC are preliminary. It has been suggested that the P-C relations of LMC in (B-V)⁰ and (V-I)⁰ have a break at $\log P = 1.0$(Tammann et al. 2002) turning to a steeper slope for longer periods. This break also implies a discontinuity of the P-L relation. The break occurs where also other Cepheid parameters change abruptly, which is attributed to a fundamental-second overtone resonance (Simon & Schmidt 1976; Simon & Lee 1981). The gap of the period distribution at 8-10 days (cf. Figs. 3 and 5) has been related to the same phenomenon (Buchler et al. 1997). Also the amplitude-color relations change their behavior near $\log P = 1.0$ (Kanbur & Ngeow 2002). We will persue the break of the P-C and P-L relations of LMC and probably SMC in Papers II and III. The simplified assumption of linear P-L relations of LMC and SMC does not alter the qualitative conclusion here from Fig. 7b that Cepheids at fixed period in different galaxies are separated in the two-color diagram.

The possible break of the P-C and P-L relations at $\log P = 1.0$in LMC and SMC questions of course their linearity in the Galaxy over the entire period interval. However, we have failed to detect any significant non-linearity of the Galactic P-C and P-L relations.

Figure 7b: A comparison of the mean position in the two-color diagram of Cepheids in the Galacty, LMC, and SMC. The loci of differentvalues of $\log P$ are indicated.

   
4 Absolute magnitude data for Galactic Cepheids from Feast and Gieren et al.

To this point we have not needed data on absolute magnitudes either for the Cepheids in the Galaxy or in the Clouds. However, in all that follows, we now do require them. Final definitive values are derived in the Sect. 6, based on new consistent absorption-to-reddening ratios, ${{\cal R}_{B,V,I}}$, in B, V, and I calculated by an iterative method in Sect. 5. To begin the iteration we have used the absolute magnitudes of Cepheids in open clusters and associations and those from the moving photosphere method. We then work from there to our finally adopted calibrations in Sect. 6 for the P-L relations.

   
4.1 Absolute magnitudes from open clusters

Feast (1999), following Feast & Walker (1987), has compiled a list of 30 Cepheids with $\log P > 0.4$ which are members of open clusters or associations. He has based their distances on an adopted Pleiades modulus of (m-M)⁰=5.57. The much smaller HIPPARCOS distance is almost certainly due to a systematic error of the trigonometric parallaxes. Therefore the best photometric modulus of (m-M)=5.61 (Stello & Nissen 2001) is adopted here. This value agrees well with the photometric distance of Pinsonneault et al. (1998, $5.60\pm0.05$) and even with the latest result from HIPPARCOS (Makarov 2002, $5.57\pm0.06$). The Cepheid luminosities are correspondingly increased by $0\hbox{$.\!\!^{\rm m}$ }04$. Not affected by this increase is RS Pup, which has a geometrical distance. $\alpha$UMi (Walker 1987a) and CS Vel (Walker 1987b) were added. V1726 Cyg was omitted as a probable overtone pulsator (Turner et al. 1994). - For brevity we will refer to the 31 Cepheids with known distances as "open-cluster Cepheids''.

   

Table 3: Absolute B, V, I magnitudes of Cepheids in open clusters.

Cepheid	l	b	$\log P$	$\mu_0$	${E(B-V)_{{\rm corr}}}$	B	V	I	(B-V)0	${{\cal R}_B}$	MB0	MV0	MI0
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
EV Sct$^{\ast }$	23.97	-0.47	0.490	10.92	0.621	11.293	10.139	8.670	0.533	4.06	-2.150	-2.683	-3.345
CEb Cas	116.56	-1.00	0.651	12.69	0.548	12.220	11.050	9.690c	0.622	4.10	-2.716	-3.338	-3.986
V1726 Cyg$^{\ast }$	92.51	-1.61	0.627	11.02	0.297	9.885	9.006	7.986	0.582	4.07	-2.342	-2.925	-3.559
SZ Tau$^{\ast }$	179.49	-18.74	0.652	8.72	0.294	7.377	6.524	5.524	0.559	4.06	-2.535	-3.095	-3.713
CF Cas	116.58	-0.99	0.688	12.69	0.531	12.335	11.136	9.754	0.668	4.12	-2.541	-3.209	-3.901
CEa Cas	116.56	-1.00	0.711	12.69	0.562	12.070	10.920	9.470c	0.588	4.09	-2.916	-3.504	-4.223
UY Per	135.94	-1.41	0.730	11.78	0.869	12.818	11.343	9.490	0.606	4.11	-2.531	-3.137	-3.861
CV Mon	208.57	-1.79	0.731	11.22	0.702	11.607	10.304	8.646	0.601	4.10	-2.490	-3.091	-3.836
QZ Nor$^{\ast }$	329.46	-2.12	0.733	11.17	0.286	9.761	8.869	7.865	0.606	4.08	-2.574	-3.181	-3.813
V Cen	316.44	3.31	0.740	9.17	0.264	7.694	6.820	5.805	0.610	4.08	-2.553	-3.163	-3.835
$\alpha$ UMi$^{\ast }$	123.28	26.46	0.748	5.19a	0.025	2.580	1.968	1.210	0.587	4.06	-2.709	-3.297	-4.023
CS Vel	277.09	-0.77	0.771	12.59b	0.771	13.049	11.703	10.068	0.575	4.09	-2.694	-3.269	-3.902
V367 Sct$^{\ast }$	21.63	-0.83	0.799	11.32	1.208	13.390	11.560	9.210c	0.622	4.13	-2.921	-3.543	-4.323
BB Sgr	14.67	-9.01	0.822	9.11	0.276	7.920	6.934	5.832	0.710	4.12	-2.330	-3.040	-3.782
U Sgr	13.71	-4.46	0.829	9.07	0.403	7.792	6.695	5.448	0.694	4.12	-2.938	-3.633	-4.356
DL Cas	120.27	-2.55	0.903	11.22	0.479	10.119	8.969	7.655	0.671	4.12	-3.071	-3.743	-4.435
S Nor	327.75	-5.40	0.989	9.85	0.178	7.373	6.429	5.422	0.766	4.14	-3.215	-3.981	-4.757
TW Nor	330.36	0.30	1.033	11.47	1.214	13.672	11.667	9.287	0.791	4.21	-2.906	-3.697	-4.498
V340 Nord	329.75	-2.23	1.053	11.17	0.323	9.526	8.370	7.168	0.833	4.18	-2.995	-3.828	-4.610
VY Car	286.55	1.21	1.277	11.63	0.260	8.630	7.465	6.271	0.905	4.21	-4.094	-4.999	-5.855
RU Sct	28.19	0.23	1.294	11.60	0.930	11.135	9.463	7.472	0.742	4.17	-4.345	-5.087	-5.869
RZ Vel	262.88	-1.91	1.310	11.19	0.293	8.209	7.082	5.856	0.834	4.18	-4.204	-5.038	-5.884
WZ Sgr	12.11	-1.32	1.339	11.26	0.428	9.428	8.027	6.528	0.973	4.25	-3.649	-4.622	-5.565
SW Vel	266.19	-3.00	1.370	12.08	0.337	9.272	8.120	6.835	0.815	4.17	-4.215	-5.030	-5.876
T Mon	203.63	-2.55	1.432	11.14	0.195	7.292	6.125	4.980	0.972	4.24	-4.672	-5.645	-6.537
KQ Sco	340.39	-0.75	1.458	12.36	0.839	11.747	9.810	7.657	1.098	4.32	-4.241	-5.339	-6.401
U Car	289.06	0.04	1.589	11.46	0.287	7.465	6.282	5.052	0.896	4.21	-5.203	-6.099	-6.955
RS Pup	252.43	-0.19	1.617	11.28	0.453	8.462	7.034	5.490	0.975	4.25	-4.744	-5.719	-6.674
SV Vul	63.95	0.32	1.653	11.83	0.518	8.671	7.209	5.691	0.944	4.24	-5.356	-6.300	-7.144
GY Sge	54.94	-0.55	1.713	12.65	1.236	12.435	10.150	7.500	1.049	4.32	-5.557	-6.606	-7.649
S Vul	63.41	0.89	1.838	13.24	0.737	10.851	8.962	6.941	1.152	4.34	-5.588	-6.740	-7.803

^a Independent of Pleiades.
^b Walker (1987b).
^c I magnitude from Sandage et al. (1999).
^d Not listed in Table 1, because designated as CEP (not yet DCEP) by Berdnikov et al. (2000).
$^{\ast }$ Remarks to individual Cepheids:
EV Sct probable overtone pulsator; bright (Cepheid?) companion (Egorova & Kovtyukh 2001); omitted.
V1726 Cyg may be an overtone pulsator (Turner et al. 2001; Usenko et al. 2001). It is listed here with its observed period.
SZ Tau probable overtone pulsator; the inferred fundamental period of $P_0=4\hbox{$.\!\!^{\rm d}$ }482$ (Turner 1992) is listed, assuming P₁/P₂=0.71.
QZ Nor (=HD144972) probable overtone pulsator (Moffett & Barnes 1986); the inferred fundamental period of $P_0=5\hbox{$.\!\!^{\rm d}$ }408$ is listed.
$\alpha$ UMi probable overtone pulsator (Evans et al. 2002); the inferred fundamental period of $P_0=5\hbox{$.\!\!^{\rm d}$ }5910$ is listed.
V367 Sct double-mode Cepheid; the fundamental period is listed (Berdnikov et al. 1995).

The data for the open-cluster Cepheids are compiled in Table 3. Columns 1, 4, and 5 are taken from Feast (1999) with the above revisions. Columns 2 and 3 give the Galactic longitude and latitude. The color excess ${E(B-V)_{{\rm corr}}}$ in Col. 6 is from Fernie et al. (1995), but corrected by Eq. (2). The B, V, I magnitudes of the intensity mean in Cols. 7-9 are from Berdnikov et al. (2000) and in three cases from Sandage et al. (1999). The dereddened colors (B-V)⁰ are shown in Col. 10. The color-dependent absorption coefficients ${{\cal R}_B}$ as derived in Sect. 5, are listed in Col. 11 (Note: ${\cal R}_{V} = {\cal R}_{B} - 1.00$, ${\cal R}_{I} = {\cal R}_{B} - 2.28$ always). The resulting absorption corrected absolute magnitudes  M_B,V,I⁰ are given in the last three columns.

   
4.2 Absolute magnitudes from expansion parallaxes

Expansion parallaxes of 34 Galactic Cepheids have been derived by Gieren et al. (1998) from the Baade-Becker-Wesselink (BBW) method as revised by Barnes & Evans (1976).

The data for the 34 Cepheids are laid out in Table 4. The Table is organized like Table 3. Columns 1, 4, and 5 are from Gieren et al. (1998). The Galactic coordinates are in Cols. 2 and 3. The ${E(B-V)_{{\rm corr}}}$ of Fernie et al. (1995), corrected by Eq. (2), are in Col. 6. The apparent magnitudes B, V, I (Cols. 7-9) are from Gieren et al. (1998) with slight revisions where available from Berdnikov et al. (2000). The dereddened colors (B-V)⁰ are shown in Col. 10. The color-dependent absorption values ${{\cal R}_B}$ (Col. 11) are analogous to those in Table 3. Again, the finally adopted absolute magnitudes are in Cols. 12-14.

 

 

Table 4: Absolute B, V, I magnitudes of Cepheids with distances from Gieren et al. (1998) ($^{\ast }$cf. notes in Table 3).

Cepheid	l	b	$\log P$	$\mu_0$	${E(B-V)_{{\rm corr}}}$	B	V	I	(B-V)0	${{\cal R}_B}$	MB0	MV0	MI0
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
EV Sct$^{\ast }$	23.97	-0.47	0.490	11.066	0.621	11.293	10.139	8.670	0.533	4.07	-2.302	-2.835	-3.497
BF Oph	357.08	8.57	0.609	9.496	0.247	8.201	7.340	6.360	0.614	4.09	-2.306	-2.919	-3.578
SZ Tau$^{\ast }$	179.49	-18.74	0.652	8.090	0.294	7.377	6.524	5.524	0.559	4.07	-1.908	-2.467	-3.086
T Vel	265.55	-3.78	0.667	10.094	0.271	8.969	8.035	6.959	0.663	4.11	-2.239	-2.902	-3.626
CV Mon	208.57	-1.79	0.731	10.901	0.702	11.607	10.304	8.646	0.601	4.11	-2.178	-2.779	-3.524
QZ Nor$^{\ast }$	329.46	-2.12	0.733	11.095	0.286	9.761	8.869	7.865	0.606	4.09	-2.501	-3.108	-3.741
V Cen	316.44	3.31	0.740	9.302	0.264	7.694	6.820	5.805	0.610	4.09	-2.687	-3.297	-3.969
CS Vel	277.09	-0.77	0.771	12.713	0.771	13.049	11.703	10.068	0.575	4.10	-2.825	-3.400	-4.032
BB Sgr	14.67	-9.01	0.822	9.238	0.276	7.920	6.934	5.832	0.710	4.13	-2.461	-3.170	-3.913
U Sgr	13.71	-4.46	0.829	8.869	0.403	7.792	6.695	5.448	0.694	4.13	-2.741	-3.436	-4.159
S Nor	327.75	-5.40	0.989	9.918	0.178	7.373	6.429	5.422	0.766	4.15	-3.285	-4.051	-4.826
XX Cen	309.46	4.64	1.040	10.847	0.258	8.795	7.819	6.736	0.718	4.14	-3.120	-3.838	-4.585
V340 Nord	329.75	-2.23	1.053	11.498	0.323	9.526	8.370	7.168	0.833	4.19	-3.327	-4.159	-4.941
UU Mus	296.82	-3.24	1.066	12.260	0.400	10.933	9.783	8.489	0.750	4.16	-2.991	-3.741	-4.515
U Nor	325.65	-0.16	1.102	10.769	0.862	10.844	9.228	7.349	0.754	4.18	-3.531	-4.285	-5.043
BN Pub	247.90	1.07	1.136	12.924	0.417	11.085	9.890	8.557	0.778	4.17	-3.579	-4.357	-5.148
LS Pubd	246.38	0.13	1.151	13.732	0.460	11.677	10.452	9.069	0.765	4.17	-3.971	-4.736	-5.522
VW Cen	307.57	-1.57	1.177	13.014	0.417	11.608	10.250	8.753	0.941	4.24	-3.176	-4.117	-5.072
VY Car	286.55	1.21	1.277	11.419	0.260	8.630	7.465	6.271	0.905	4.22	-3.886	-4.791	-5.647
RY Sco	356.49	-3.42	1.308	10.469	0.714	9.477	8.012	6.276	0.751	4.17	-3.971	-4.722	-5.531
RZ Vel	262.88	-1.91	1.310	11.169	0.293	8.209	7.082	5.856	0.834	4.19	-4.186	-5.020	-5.866
WZ Sgr	12.11	-1.32	1.339	11.262	0.428	9.428	8.027	6.528	0.973	4.26	-3.655	-4.628	-5.571
WZ Car	289.30	-1.18	1.362	12.980	0.362	10.409	9.259	7.973	0.788	4.17	-4.082	-4.870	-5.685
VZ Pub	243.42	-3.31	1.365	13.551	0.452	10.782	9.626	8.300	0.704	4.14	-4.642	-5.345	-6.083
SW Vel	266.19	-3.00	1.370	11.989	0.337	9.272	8.120	6.835	0.815	4.18	-4.127	-4.942	-5.789
T Mon	203.63	-2.55	1.432	10.576	0.195	7.292	6.125	4.980	0.972	4.25	-4.110	-5.083	-5.975
RY Vel	282.57	1.48	1.449	12.100	0.554	9.735	8.372	6.826	0.809	4.19	-4.688	-5.497	-6.322
AQ Pub	246.16	0.11	1.479	12.750	0.531	10.067	8.704	7.144	0.832	4.20	-4.915	-5.746	-6.616
KN Cen	307.76	-2.11	1.532	12.911	0.774	11.466	9.853	7.990	0.839	4.22	-4.706	-5.546	-6.403
l Car	283.20	-7.00	1.551	8.941	0.160	5.000	3.737	2.563	1.103	4.30	-4.631	-5.734	-6.699
U Car	289.06	0.04	1.589	11.069	0.290	7.465	6.282	5.052	0.893	4.22	-4.827	-5.720	-6.573
SV Vul	63.95	0.32	1.653 var	12.325	0.518	8.671	7.209	5.691	0.944	4.25	-5.856	-6.800	-7.644
GY Sge	54.94	-0.55	1.713 var	12.939	1.236	12.435	10.150	7.500	1.049	4.33	-5.858	-6.907	-7.950
S Vul	63.41	0.89	1.838 var	13.731	0.737	10.851	8.962	6.941	1.152	4.35	-6.086	-7.238	-8.301

   
5 Absorption-to-reddening ratios in B, V, and I for Cepheids

   
5.1 Mean values of ${{\cal R}_B}$, ${{\cal R}_V}$, and ${{\cal R}_I}$ and their dependence on intrinsic color

In Sect. 2 the color excesses ${E(B-V)_{{\rm corr}}}$ and ${E(V-I)_{\rm corr}}$ could be derived for Cepheids. The next step is to derive the absorption coefficients ${\cal R}_{B,V,I}=\frac{A_{B,V,I}}{E(B-V)}$. The Cepheid distances provided by Feast (Table 3) and Gieren et al. (Table 4) are ideally suited for this purpose.

However, we have omitted five Cepheids which are known or suspected to be overtone pulsators as well as EV Sct which has a bright companion. We have also omitted the three Cepheids with BBW distances with long, yet variable periods; they do not render well to the BBW method. This leaves 25 Cepheids in Feast's list (Table 3) and 28 Cepheids in Gieren's et al. list (Table 4).

Figure 8: The provisional P-L relations in B, V, and I for Galactic Cepheids in open clusters ( left panels) and with BBW distances ( right panels). The Cepheids shown as triangles are not used for the solution; at short periods they are probable overtone pulsators (shown here with their inferred fundamental period), the three long period Cepheids with BBW distances have variable periods.

As a first step, provisional absolute magnitudes $M_{B,V,I}^{\rm prov}=m_{B,V,I}-\mu_{0}-A_{B,V,I}^{\rm prov}$ are formed with the data in Tables 3 and 4. The values $A_{B,V,I}^{\rm prov}$ are determined from ${E(B-V)_{{\rm corr}}}$ in Col. 6 and on the assumption that ${\cal R}_{B}^{\rm prov}=4.32$, ${\cal R}_{V}^{\rm prov}=3.32$, and ${\cal R}_{I}^{\rm prov}=1.94$ (cf. Schlegel et al. 1998). The corresponding values $M_{B,V,I}^{\rm prov}$ are plotted against $\log P$. The resulting provisional P-L relations are shown in Fig. 8. However, the residuals $\Delta M = M_{\rm obs} - M_{\rm mean}$ are still a function of ${E(B-V)_{{\rm corr}}}$(Fig. 9).

The brightening of the Cepheids with increasing ${E(B-V)_{{\rm corr}}}$ cannot be due to the color excesses themselves, which have been freed of systematic effects. They must be explained by too large absorption corrections, i.e. by an overestimate of the provisional values ${{\cal R}_{B,V,I}}$. A reduction of the latter improves the situation. After two more iterations any dependence of the Cepheid magnitude on ${E(B-V)_{{\rm corr}}}$ is removed. The corresponding ${\cal R}$ values are ${\cal R}_{B}=4.13\pm0.15$, ${\cal R}_{V}=3.20\pm0.13$, and  ${\cal R}_{I}=1.89\pm0.12$.

Figure 9: The magnitude residuals $\Delta M_{B,V,I}$ off the mean provisional P-L relations in function of the color excess ${E(B-V)_{{\rm corr}}}$. Closed circles are data from Table 3 (left panel of Fig. 8), open circles are data from Table 4 (right panel of Fig. 8).

The absorption coefficients ${\cal R}$ must also obey the condition in Eq. (6); it holds in addition that ${\cal R}_{V}\equiv {\cal R}_{B} - 1$. This leads to the best compromise values of:

$$% {\cal R}_{B}=4.17\pm0.15, {\cal R}_{V}=3.17\pm0.13, {\cal R}_{I}=1.89\pm0.12.$$ (7)

The solutions in Eq. (7) hold, strictly speaking, for only the present sample of 53 calibrating Cepheids which have a median color of $(B-V)^0_{\rm med}=0.78$ and a median excess of $E(B-V)_{\rm med}=0.42$. The exact values of ${{\cal R}_{B,V,I}}$ must depend on intrinsic color of the Cepheids and slightly on the size of the color excess. The dependence is generally written as (normalized for the present case)

$$% \Delta {\cal R}_{B,V,I} = \alpha \left[(B-V)^0 - 0.78\right] + 0.05\left[E(B-V)_{\rm corr} - 0.42\right],$$ (8)

where $\alpha$ has been found to be 0.28 (Schmidt-Kaler 1965) or 0.25 (Olson 1975) for "normal stars''. However, an analysis of Ib supergiant spectra requires a value of $\alpha =0.44$ (Buser 1978). This value is accepted here as the most appropriate one for Cepheids. The values of $\Delta {\cal R}$ in B, V, and I must necessarily be the same; otherwise one would create P-C relations from absolute magnitudes which differed from the P-C relations in Eqs. (3) and (5), which are independent of any adopted value of ${\cal R}$ (cf. Sect. 6.1).

The present assumption of $\alpha$ in Eq. (8) being color-independent is not exact, but it is required here because of the linear approximation between E(V-I) and E(B-V) in Eq. (4). This linear approximation and the corresponding constancy of $\alpha$ are, however, justified for the restricted color range of the Cepheids under consideration.

   
5.2 Are the ${{\cal R}_{B,V,I}}$ values dependent on Galactic longitude?

As a test for systematic errors, we inquire in this section if our ${\cal R}$ values depend on position in the Galaxy. It is known the ${\cal R}$ values may show variations in special regions such as the Orion Nebula, as first discovered and discussed by Baade & Minkowski (1937), and apparently verified by Sharpless (1952). A comprehensive summary by Sharpless (1963) reviewed the evidence from many studies up to 1962 where only a few large variations of ${\cal R}$ with environment had been found.

However, Johnson (1966), in a controversial summary article, suggested instead that large systematic variations of ${\cal R}$ with Galactic longitude exist (his Fig. 41 and Table 30), reaching values of A_V/E(B-V) = 6 near Galactic longitude $150^{\circ}$, with the variation increasing to this level over the canonical value of 3.8 over a longitude range from $100^{\circ}$ to $210^{\circ}$. If true, this would be most serious for our problem here, introducing unacceptable errors in our finally adopted absolute magnitudes in Tables 3 and 4.

We have tested for systematic variations of ${{\cal R}_{B,V,I}}$with longitude for the Cepheids in Tables 3 and 4 by forming the ratios, $(M_{\rm obs}-M_{\rm PL})/E(B-V)_{\rm corr}$, of the individual absolute magnitude residuals from our final ridge-line P-L relations (Eqs. (15), (16), and (17) later) to our corrected ${E(B-V)_{{\rm corr}}}$ excess values. Figure 10 shows the lack of correlation of these ratios with Galactic longitude. There is no obvious correlation.

   
6 The Galactic P-L relations

   
6.1 The calibrated Galactic P-L relations

With the distances of the calibrating Galactic Cepheids of Feast (Table 3) and Gieren et al. (Table 4), and the corrected color excesses ${E(B-V)_{{\rm corr}}}$ from Sect. 2.3 as well as the new absorption coefficients ${{\cal R}_{B,V,I}}$ in Sect. 5, one can derive absolute magnitudes M⁰_B,V,I. They lead to two independent sets of P-L relations:
Open clusters (n= 25)

   

$$M^{0}_{B} = -(2.755\pm0.154)\log P - 0.526\pm0.184, \sigma=0.28$$ (9)

$$M^{0}_{V} = -(3.175\pm0.139)\log P - 0.850\pm0.167, \sigma=0.26$$ (10)

$$M^{0}_{I} = -(3.468\pm0.134)\log P - 1.328\pm0.160, \sigma=0.25,$$ (11)

and BBW (n= 28)

   

$$M^{0}_{B} = -(2.765\pm0.166)\log P - 0.416\pm0.197, \sigma=0.25$$ (12)

$$M^{0}_{V} = -(3.097\pm0.142)\log P - 0.820\pm0.169, \sigma=0.22$$ (13)

$$M^{0}_{I} = -(3.326\pm0.128)\log P - 1.356\pm0.152, \sigma=0.19.$$ (14)

The agreement of slope of the two sets - well within statistics - is impressive. The BBW calibration is fainter (at $\log P = 1.0$) by $0\hbox{$.\!\!^{\rm m}$ }10$ in B, $0\hbox{$.\!\!^{\rm m}$ }11$ in V, and $0\hbox{$.\!\!^{\rm m}$ }12$ in I than the open-cluster calibration. This is as satisfactory as can be hoped for.

Also the scatter of $\sigma=0\hbox{$.\!\!^{\rm m}$ }3$ in Eqs. (9-11) is as small as can be expected considering the error of the distances of clusters and associations, the possibility of the inclusion of non-members of clusters and particularly of associations, and the large absorption corrections. The scatter of the BBW P-L relations is even smaller.

Since there is no objective way to weight the two independent sets of P-L relations, the data are combined to determine the mean P-L relations (n=53):

   

$$M^{0}_{B} = -(2.757\pm0.112)\log P - 0.472\pm0.133, \sigma=0.27$$ (15)

$$M^{0}_{V} = -(3.141\pm0.100)\log P - 0.826\pm0.119, \sigma=0.24$$ (16)

$$M^{0}_{I} = -(3.408\pm0.095)\log P - 1.325\pm0.114, \sigma=0.23.$$ (17)

These relations are shown in Fig. 11. - The relations are believed to hold down to $\log P = 0.4$ although the calibrators with the shortest periods have $\log P\ga 0.6$. The linear extrapolation seems justified in view of the linearity of the P-C relations in (B-V)⁰ and (V-I)⁰ (Eqs. (3) and (5)) down to $\log P = 0.4$. This could be brought about by P-L relations with variable slope below $\log P=0.6$ only by a concerted change of slope in B, V, and I, which seems contrived.

It is reassuring that the subtractions of Eq. (16) from (15) and (17) from (16) leads to the following P-C relations

$$% (B-V)^0 = (0.384\pm0.150)\log P + 0.354\pm0.179$$ (18)

$$(V-I)^0 = (0.267\pm0.138)\log P + 0.500\pm0.165,$$ (19)

which are the same as in Eqs. (3) and (5) to within the (small) errors. This proves - since the latter two equations are derived without any cognizance of the value of ${\cal R}$ - that the present absorption corrections are at least selfconsistent. This selfconsistency is destroyed if one uses - as some authors have proposed - different values of the coefficient $\alpha$ in Eq. (8) for the different wavebands B, V, and I.

Other systematic errors which might have been introduced by the present reduction procedures are discussed in Sect. 6.3.

Figure 10: The lack of correlation with Galactic longitude for the ratio of absolute magnitude residuals from the adopted P-L relations in Eqs. (15-17) to the corrected ${E(B-V)_{{\rm corr}}}$ color excess values for individual Cepheids in Tables 3 and 4. Closed circles are for Cepheids in Table 3. Open circles are Cepheids from Table 4.

Figure 11: The combined P-L relations in B, V, and I from 25 Cepheids in open clusters (filled symbols) and 28 Cepheids with BBW distances (open symbols). Triangles are not used for the solution (cf. caption to Fig. 8). - The square in the M0V and M0I panels are from the HIPPARCOS calibration (Groenewegen & Oudmaijer 2000). - Upper and lower boundaries of the P-L relations are shown on the assumption that the constant-period lines have slopes of 3.52, 2.52, and 1.94 in B, V, and I, respectively, and that the instability strip has a width of $\pm0\hbox{$.\!\!^{\rm m}$ }13$ in (B-V)0 and $\pm0\hbox{$.\!\!^{\rm m}$ }10$ in (V-I)0 (cf. Fig. 15). The calculations use ${E(B-V)_{{\rm corr}}}$ values, $\alpha =0.44$, and the ${{\cal R}_{B,V,I}}$ values, corrected for intrinsic color, as listed in Col. 11 of Tables 3 and 4.

There is one independent method of checking the zero point of the P-L relation. Groenewegen & Oudmaijer (2000) have used 236 carefully selected Cepheids with HIPPARCOS parallaxes to calibrate a P-L relation in V and I with preselected slope. But their values of $M_V=-3.72\pm0.11$ and $M_I=-4.41\pm0.12$ at $\log P=0.85$ - the median period of their sample - should be quite independent of any adopted slope. This solution is very close to the earlier solution by Feast & Catchpole (1997) based on fewer, but high-weight Cepheids. The quoted magnitudes are made here somewhat fainter for the following reason.The authors have adopted instead of individual color excesses E(B-V) the mean P-C relations in (B-V)⁰ by Laney & Stobie (1995) and (V-I)⁰ by Caldwell & Coulson (1986) which, averaged over all periods, agree sufficiently well with Eqs. (3) and (5). The adopted values of E(B-V) have necessarily considerable scatter, but the systematic errors should be small. However Groenewegen & Oudmaijer (2000) have adopted variable absorption coefficients which amount to ${\cal R}_V=3.3$ and ${\cal R}_I=2.0$ on average. These values appear now to be too high. With ${\cal R}_{V}=3.17$ and ${\cal R}_{I}=1.89$ from Eq. (7) and a median extinction of E(B-V)=0.43 for their sample the magnitudes are overcorrected for absorption by $0\hbox{$.\!\!^{\rm m}$ }06$ on average in V and I. These corrections have been included in the absolute magnitudes quoted above.

The HIPPARCOS calibration is hence brighter than the adopted P-L relations by $0\hbox{$.\!\!^{\rm m}$ }21\pm0.11$ in B and $0\hbox{$.\!\!^{\rm m}$ }18\pm0.12$ in I. If one would average this determination with the calibration through open clusters and BBW distances, giving equal weights, the zero point would shift to brighter magnitudes by $0\hbox{$.\!\!^{\rm m}$ }06$- $0\hbox{$.\!\!^{\rm m}$ }07$. This suggests that the adopted P-L relations are reliable to within $\sim\!0\hbox{$.\!\!^{\rm m}$ }1$.

   
6.2 Metallicity effects on the P-L relation?

Fry & Carney (1997) have measured metallicities of 14 calibrating Cepheids in Table 3, two of which are overtone pulsators; they have been excluded in the following. Eight of the fundamental pulsators have also BBW distances from Gieren et al. (1998). If one plots the magnitude residuals $\Delta M_{B,V,I}$ off the P-L relations in Fig. 11 one finds a barely significant correlation with [Fe/H]. The sense is that metal-poor Cepheids are fainter. This is opposite to all model calculations and to the evidence of the metal-poor LMC Cepheids (cf. Sect. 6.3).

The suspicion then is that metal-poor Cepheids are undercorrected for absorption. This can be if the ${E(B-V)_{{\rm corr}}}$ are still inflicted by a metallicity effect, i.e. the color excesses of metal-poor Galactic Cepheids are too small. This is indeed a constant worry if E(B-V) is determined from the photometry of the Cepheids themselves. If this interpretation is correct, the metal-poor Cepheids must appear to be also redder, which is physically most unlikely. In order to test this, the color residuals $\Delta (B-V)$ and $\Delta (V-I)$ off the P-C relations in Eqs. (3) and (5) are plotted against [Fe/H] for the (only) 12 Cepheids with known [Fe/H] in Fig. 12.

Figure 12: Color residuals $\Delta (B-V)$ of the calibrating Galactic Cepheids with known metallicities in function of [Fe/H]. The red color of the metal-poor Cepheids must be due to systematic errors of the adopted color excesses ${E(B-V)_{{\rm corr}}}$. Triangles stand for Cepheids with variable periods; they are not used for the solution.

The metal-poor Cepheids appear indeed to be redder. Again, the only explanation for this is to assume that the adopted color excesses ${E(B-V)_{{\rm corr}}}$ are too small for metal-poor Cepheids. If the ${E(B-V)_{{\rm corr}}}$ are underestimated by roughly

$$% \Delta E(B-V) = E(B-V)_{\rm true} - E(B-V)_{\rm corr} \approx -0.12 \mbox{[Fe/H]},$$ (20)

then the redness of metal-poor Cepheids is explained in (B-V) and roughly also in (V-I). Moreover, if one multiplies $\Delta E(B-V)$ with the values of ${{\cal R}_{B,V,I}}$ one recovers reasonably well the slopes of the above-mentioned correlation between magnitude residuals and [Fe/H].

It must be added that Eq. (20) does not reflect the full dependence of the color excesses on metallicity. The correction is derived on the assumption that the intrinsic colors of Cepheids were independent of [Fe/H], but actually metal-poor Cepheids are expected to be bluer. The coefficient in Eq. (20) should therefore be larger by a yet undetermined amount.

As a consequence the P-C and P-L relations derived here apply to Galactic Cepheids with the mean metallicity of the calibrators, i.e. a value presumably not far from [Fe/H] =0.

   
6.3 Comparison with previous P-L relations

   
6.3.1 Comparison with previous Galactic relations

In Table 5 previous Galactic P-L relations are compared with the present results. It is obvious that the earlier adopted P-L relations in B, V, and I are too flat. This is no surprise because it had been assumed that the slope in the Galaxy and the average slope in LMC are the same. The steepness of the Galactic slope is accentuated by the exclusion of EV Sct, which has a bright companion, and of the relatively bright overtone pulsators at short periods.

 

 

Table 5: Galactic P-L relations by different authors. The coefficients a and b are given for a P-L relation of the form $M=a(\log P -1)+b$.

Authors	MB		MV		MI
	a	b	a	b	a	b
Kraft (1961)	-2.25	-3.58	-2.54	-4.21	$\cdots$	$\cdots$
Sandage & Tammann (1968)	-2.50	-3.61	-2.76	-4.24	$\cdots$	$\cdots$
Feast & Walker (1987)	$\cdots$	$\cdots$	-2.78	-4.24	$\cdots$	$\cdots$
Madore & Freedman (1991)	$\cdots$	$\cdots$	-2.76	-4.16	-3.06	-4.87
Gieren et al. (1993)	$\cdots$	$\cdots$	-2.99	-4.36	$\cdots$	$\cdots$
Laney & Stobie (1994)	$\cdots$	$\cdots$	-2.87	-4.07	$\cdots$	$\cdots$
Feast & Catchpole (1997)	$\cdots$	$\cdots$	-2.81	-4.24	$\cdots$	$\cdots$
Gieren et al. (1998)	$\cdots$	$\cdots$	-2.77	-4.06	-3.04	-4.77
present paper	-2.76	-3.23	-3.14	-3.97	-3.41	-4.73

Hand in hand with the steep slope here, the new calibration is considerably fainter at $\log P = 1.0$ by up to $0\hbox{$.\!\!^{\rm m}$ }4$ than previous values in Table 5. The difference is only partially due to the absorption corrections which are smaller here than adopted by most authors, because the color excesses E(B-V)by Fernie et al. (1995) had to be reduced here by 5% and the ${{\cal R}_{B,V,I}}$ values appropriate for Cepheids were found to be somewhat smaller than adopted by some authors.

Figure 13: Comparison of the present Galactic P-L relations in B, V, and I with model calculations (see text). BA is Baraffe & Alibert (2001).

The discrepancy in absolute magnitude decreases towards longer periods. At $\log P =1.5$ the M_V magnitudes of all authors agree to within $0\hbox{$.\!\!^{\rm m}$ }12$ (except the very bright value of Gieren et al. 1993). The new M_I magnitude at $\log P =1.5$ is brighter by $0\hbox{$.\!\!^{\rm m}$ }04$ than the one from the widely used P-L relation of Madore & Freedman (1991).

   
6.3.2 Comparison with model calculations

The P-L relations in Eqs. (15-17) are compared in Fig. 13 with the results of model calculations for the case of $\mbox{[Fe/H]}=0$. The observed slopes in B and V lie between the calculated slopes by SBT (based on Geneva models) and Baraffe & Alibert (2001). The agreement of the slopes in I is nearly perfect. The curved P-L relations of Caputo et al. (2000) are not realistic. The reason is probably their reliance on the calculated position of the red edge of the instability strip (Bono et al. 1999), which is sensitive to the treatment of convection.

The zero point at $\log P = 1.0$ of Baraffe & Alibert (2001) is somewhat bright, viz. by $0\hbox{$.\!\!^{\rm m}$ }07$ in B to $0\hbox{$.\!\!^{\rm m}$ }17$ in I. SBT have calculated the luminosities of pulsating models by Chiosi et al. (1992), Schaerer et al. (1993, and references therein), and Saio & Gautschy (1998). The results are similar; the ones from the Schaerer et al. models are taken here as an example. SBT refer to the blue edge of the instability strip. Assuming half-widths of the instability strip of roughly $\Delta M =0\hbox{$.\!\!^{\rm m}$ }4$, $0\hbox{$.\!\!^{\rm m}$ }3$, and $0\hbox{$.\!\!^{\rm m}$ }2$ in B, V, and I, respectively, the calculated luminosities for the middle of the strip have been reduced by the corresponding amounts. They turn out to be brighter than observed; at $\log P = 1.0$ the difference is $0\hbox{$.\!\!^{\rm m}$ }54$ in B and decreases to $0\hbox{$.\!\!^{\rm m}$ }39$ in I. The non-linear P-L relations of Caputo et al. (2000) start out quite bright at $\log P = 0.4$ to become fainter than observed by $0\hbox{$.\!\!^{\rm m}$ }5$- $0\hbox{$.\!\!^{\rm m}$ }9$ at  $\log P =1.5$ depending on the waveband. In view of the very faint luminosities at long periods their upward revision of H₀ ($\ga$$69\;$km s^-1Mpc^-1) is unwarranted.

The conclusion is that it is not yet possible to derive reliable luminosities of Galactic Cepheids from theory over the entire period range. The best agreement is provided by Baraffe & Alibert (2001) whose B, V, I magnitudes at $\log P=1.6$ agree fortuitously well within $0\hbox{$.\!\!^{\rm m}$ }02$ with the observed ones.

   
6.3.3 Comparison with LMC and SMC

The apparent P-L relations of LMC are very well defined because of the excellent B, V, I photometry in the Johnson-Landolt-Cape-Cousins systems (cf. Sandage 1997) of 650 Cepheids in the fundamental mode by Udalski et al. (1999b). These authors have also determined good color excesses E(B-V) from nearby red-clump giants; they are independent of the metallicity of the Cepheids. Since the excesses are relatively small, $0\hbox{$.\!\!^{\rm m}$ }0 < E(B-V) < 0\hbox{$.\!\!^{\rm m}$ }2$, any of their possible errors cannot alter the following conclusions.

To show the difference between the P-L relations of the Galaxy and LMC the 650 LMC Cepheids are plotted in Fig. 14a with the mean Galactic P-L relations from Eqs. (15-17) overplotted. The LMC P-L relations are flatter in all three wave bands than the Galactic ones. This and the color differences are the main conclusion of the paper.

Figure 14a: The position of 650 absorption-corrected fundamental-mode LMC Cepheids from Udalski et al. (1999b) in the P-L plane. The adopted LMC modulus is (m-M)0=18.54. Open symbols are Cepheids excluded by Udalski et al. (1999a). Overplotted are the mean Galactic P-L relations from Eqs. (15-17).

For the comparison of the LMC and Galactic Cepheids in Fig. 14a a Cepheid-independent distance modulus of LMC was adopted. The relevant data are compiled in Table 6. The straight and weighted means of the entries are equal to $(m-M)^0_{\rm LMC}=18.54$. - Table 6 contains also the latest results from eclipsing binaries and red-clump stars. These two methods were formerly suggested to give a significantly lower LMC modulus. The low luminosities in the literature based on statistical parallaxes of Galactic RR Lyr stars are very sensitive to sample selection and unreconcilable with other calibrations; they are given zero weight (cf. Walker 1999; Zaritsky 1999).

 

 

Table 6: The Distance Modulus of LMC independent of the P-L relation of Cepheids.

Authors	$\mu^0$	Method
Van Leeuwen et al. (1997)	$18.54\pm0.18$	HIPPARCOS parallaxes of Miras
Panagia (1999)	$18.58\pm0.05$	Ring around SN 1987A
Walker (1999)	$18.54\pm0.08$	Eclipsing binary, SN 1987A ring, Miras, RR Lyr
Sandage et al. (1999)	$18.56\pm0.10$	RR Lyr
Kovács (2000)	$18.52(\pm0.10)$	Double mode RR Lyr
Sakai et al. (2000)	$18.59\pm0.09$	Tip of RGB
Cioni et al. (2000)	$18.55\pm0.04$	Tip of RGB
Romaniello et al. (2000)	$18.59\pm0.09$	Tip of RGB
Whitelock & Feast (2000)	$18.64\pm0.14$	HIPPARCOS parallaxes of Miras
Groenewegen & Salaris (2001)	$18.42\pm0.07$	Eclipsing binary
Girardi & Salaris (2001)	$18.55\pm0.05$	Red-clump stars
Pietrzynski & Gieren (2002)	$18.47(\pm0.10)$	Tip of RGB
Keller & Wood (2002)	$18.55(\pm0.02)$	Models of bump Cepheids
Adopted	$18.54\pm0.02$	(statistical)

At $\log P = 0.4$ the LMC Cepheids are brighter by $0\hbox{$.\!\!^{\rm m}$ }61$, $0\hbox{$.\!\!^{\rm m}$ }50$, and $0\hbox{$.\!\!^{\rm m}$ }46$ in B, V, and I, respectively, than their Galactic counterparts; their overluminosity decreases towards $\log P = 1.0$. Then above at $\log P \sim 1.4$ Galactic Cepheids are brighter. Of course, the crossing point can be shifted towards shorter periods by increasing the Galactic calibration within the errors ( $\sim\!0\hbox{$.\!\!^{\rm m}$ }1$) or/and by arbitrarily decreasing the LMC distance. But it is impossible to reach agreement between the Galactic and LMC P-L relations, because their slopes are different.

Any attempt to derive an accurate Cepheid distance of LMC by means of a calibrated Galactic P-L relation is therefore highly compromised over the entire period range (see Sects. 8 and 9). The resulting distance will be a function of period in any case, the amplitude in $\Delta(m-M)$ being $\sim$ $0\hbox{$.\!\!^{\rm m}$ }5$ in all three colors, i.e. larger distances at longer periods.

The difference of the P-L relations in different galaxies does not come as a total surprise. Already Laney & Stobie (1994) had convincingly shown that the SMC Cepheids are bluer in (B-V) than those in LMC and in the Galaxy similar to Fig. 6a. This implies that at least the P-L relation in B or/and in V cannot be the same in the three galaxies.

The comparison of the Galactic P-L relations with those of SMC is shown in Fig. 14b on the assumption that  $(m-M)_{\rm SMC}^0=19.00$ (SBT). It is obvious, independent of any distance, that the P-L relations in B, V, and I of SMC are flatter than those of the Galaxy.

Figure 14b: The position of 489 absorption-corrected fundamental-mode SMC Cepheids from Udalski et al. (1999c) in the P-L plane. The adopted SMC modulus is (m-M)0=19.00. Symbols as in Fig. 14a.

   
6.4 Tests for systematic errors

The fist question as to systematic errors concerns the zero points of the adopted color excesses E(B-V). Fernie's own Galactic zero point is confirmed to within a mean difference of  $0\hbox{$.\!\!^{\rm m}$ }012\pm0\hbox{$.\!\!^{\rm m}$ }025$by nine external sources (cf. Table 2). As discussed in Sects. 2.3 and 2.4, the adopted intrinsic colors also agree with those of Laney & Stobie (1994) in (B-V)⁰ to within  $0\hbox{$.\!\!^{\rm m}$ }028$. Hence, the somewhat larger deviation of the present (V-I)⁰ colors from the early work of Caldwell & Coulson (1986) cannot be ascribed to errors in E(B-V). In view of this argument, the Galactic colors are believed to be good to within  $0\hbox{$.\!\!^{\rm m}$ }02{-}0\hbox{$.\!\!^{\rm m}$ }03$. - Also, in a forthcoming paper it will be shown that the P-L relations in B and V of LMC used here agree with those from 99 Cepheids with independent B,V photometry. The latter are taken from Laney & Stobie (1994) and a compilation by Sandage (1988); for 29 of them E(B-V) is available from Caldwell & Coulson (1986), for the remaining ones $E(B-V)=0\hbox{$.\!\!^{\rm m}$ }1$was assumed. The two sets of m_B⁰ and m_V⁰ magnitudes agree to within $0\hbox{$.\!\!^{\rm m}$ }03\pm0\hbox{$.\!\!^{\rm m}$ }06$ and $0\hbox{$.\!\!^{\rm m}$ }04\pm0\hbox{$.\!\!^{\rm m}$ }05$, respectively. This suggests that the E(B-V)s of Udalski et al. are reliable at the $0\hbox{$.\!\!^{\rm m}$ }01$ level (assuming ${\cal R}_{V}=3.17$ as in the Galaxy). Udalski's et al. color excesses for SMC Cepheids are derived in the same way as in LMC and should therefore be subject to equally small errors. The conclusion is that the errors in intrinsic color between the Galaxy, LMC, and SMC are hardly larger than $0\hbox{$.\!\!^{\rm m}$ }03$.

The next question is whether the well determined value of the Galactic extinction-absorption ratio ${{\cal R}_V}$ is also applicable to the Clouds. In view of the moderate color excesses of the Cloud Cepheids any reasonable variation of ${{\cal R}_V}$ remains, however, without consequences for the present conclusions concerning the differences of the P-L relations.

The crucial question, however, is whether the different slopes of the P-L relations of the Galaxy, LMC, and SMC could be an artefact. The consequences of the non-uniqueness of the P-L relation in Figs. 14a and b are so severe that we have made several tests to try to make the differences go away.

The slopes in the P-L relation for LMC and SMC are so well determined, based on so many stars, and the reddening corrections for both Clouds are so small that there is scarcely any doubt that the data for the Clouds in Figs. 14a,b are secure. Therefore, we must study the data and procedures for the Galaxy (Tables 3 and 4), not in LMC or SMC in searching for a possible systematic error in Figs. 11 and 14a,b.

What seems so compelling is the near perfect agreement in the independent results on distances, and therefore absolute magnitudes, between the listings by Feast (1999) and by Gieren et al. (1998). The P-L Eqs. (9-11) from the data by Feast (to be sure, as rediscussed by us for reddenings and ${\cal R}$ values) are nearly identical with Eqs. (12-14) using the rediscussed data based on Gieren et al. The agreement is emphasized by the lack of difference in Fig. 11 between the open and closed circles. Hence, if there is a systematic error in the Galactic data, its effect must be the same between the independent methods used by Feast (cluster main sequence fittings) and Gieren et al. (BBW) even through the methods are so fundamentally different.

We first ask if our new procedures of "correcting" Fernie- system reddenings by a factor of 0.951 (Eq. (2)) and/or our use of the large value of $\alpha$ in Eq. (8) as 0.44 (Buser 1978) rather than what others have used as 0.28 (Schmidt-Kaler 1965), or 0.25 (Olson 1975) could have introduced errors in the Galactic P-L slope.

What at first seemed as a possibility for a systematic error in the slope was that if E(B-V) was a function of $\log P$(larger excesses for longer period Cepheids), and if our adopted E(B-V) values were in error we could produce an effect. The same type of a priori reasoning could also be made on the effect of incorrect $\alpha$ in Eq. (8).

However, there is no correlation between the E(B-V) values in Tables 3 and 4 and the period. Large and small reddenings occur at all periods between $\log P$ of 0.6 and 1.8. Furthermore, the reddenings on the Fernie system, reduced by Eq. (2) and listed in Table 3, are nearly identical (mean difference $0\hbox{$.\!\!^{\rm m}$ }02$) with those used by Feast (1999) that were determined using the early-type stars in the clusters, entirely independently of the Cepheid procedures used for the Fernie-system reddenings. Therefore, the basis for any such a priori argumentation on E(B-V) and $\alpha$ fails.

Nevertheless, we tested directly for the effect of variations in the reddening and $\alpha$ assumptions by making a series of new reductions of the absolute magnitudes in Tables 3 and 4 using a variety of assumptions. Table 7 shows the results of first using our corrected reddenings listed in Tables 3 and 4 but using $\alpha$ values of 0.44, 0.25, and zero. We repeated the calculations using Fernie-system reddenings (not corrected by Eq. (2)) and again with the three values of $\alpha$. The slopes are extremely stable, not changing by nearly enough to eliminate the differences in Figs. 14a,b. The reason is that using ${E(B-V)_{{\rm FS}}}$ instead of  ${E(B-V)_{{\rm corr}}}$ changes the ${\cal R}$ ratios to smaller values, compensating in the absolute magnitudes for the larger ${E(B-V)_{{\rm FS}}}$.

 

 

Table 7: The sensitivity of the P-L slope from the Tables 3 and 4 data to assumptions on reddening and broad-band effects ("Corr'' refers to  ${E(B-V)_{{\rm corr}}}$ from Eq. (2); "FS'' refers to the ${E(B-V)_{{\rm FS}}}$ in the Fernie system).

E(B-V)	$\alpha$	slope	E(B-V)	$\alpha$	slope
(1)	(2)	(3)	(4)	(5)	(6)
		B -2.750			B -2.758
Corr	0.44	V -3.137	FS	0.44	V -3.142
		I -3.408			I -3.410
		B -2.710			B -2.716
Corr	0.25	V -3.096	FS	0.25	V -3.100
		I -3.368			I -3.369
		B -2.657			B -2.661
Corr	0.00	V -3.043	FS	0.00	V -3.045
		I -3.315			I -3.314

It should also be noted that Gieren et al. (1998) themselves derived a steeper slope with their Galactic data ( ${\rm d}M_{V}/{\rm d}\log P = -3.037$; ${\rm d}M_{I}/{\rm d}\log P = -3.329$), very similar to ours, of $-3.141\pm0.100$ and $-3.408\pm0.095$ (Eqs. (16) and (17)), respectively. But they abandoned their own slopes and adopted the less steep LMC slopes of -2.769 in V and -3.041 in I on the assumption that the LMC slopes are universal.

We conclude that if Figs. 14a,b are wrong, then both the Tables 3 and 4 absolute magnitudes are wrong by some systematic error that does not depend on reddening errors or the broad-band color effects corrected by Eq. (8). There would have to be errors in the absolute magnitudes derived independently by cluster fitting and by the BBW method. However, as Gieren et al. (1998) use secure temperatures derived from JHK near infrared colors where the effects of any reddening errors are small (Gieren's et al. E(B-V) reddenings differ from our corrected values in Table 4 by only $0\hbox{$.\!\!^{\rm m}$ }02$ on average) their route via the Barnes-Evans effect also seems secure.

We finally must comment on why Figs. 14a,b were so unexpected in view of the earlier result by one of us (SBT) that the Galactic Cepheids from Feast & Walker (1987) show nearly the same slope as the P-L relation for LMC, and that the equations shown there (coded in their Figs. 10 and 11) differ from Eqs. (15-17) here. There are two reasons. (1) In Tables 3 and 4 we rigorously exclude possible overtone pulsators, whereas they were not excluded in the Feast/Walker comparison. (2) Comparing the Feast/Walker data star-by-star with our Table 3 values derived by the iterated procedure for the corrected reddenings and the absorption-to-reddening ${\cal R}$ values shows that there are six Cepheids with $\log P \le 0.9$ that are brighter in Feast/Walker than in Table 3 by an average of $0\hbox{$.\!\!^{\rm m}$ }12$. These, together with the five overtone pulsators that are also brighter, skewed the least-squares correlation lines in SBT to their less steep values, nearly imitating the LMC slope.

   
7 The instability strip for the Galaxy, LMC, and SMC in the HR diagram

   
7.1 The position of the Galactic instability strip in the short- and longwave color-magnitude diagram

If the P-C relations (Eqs. (3) and (5)) are used to substitute the $\log P$ term in the P-L_V,I relations (Eqs. (16) and (17)) one obtains:

$$% M_{V}^0=(-8.58\pm0.5)(B-V)^0 + 2.27$$ (21)

$$M_{I}^0=(-13.31\pm1.0)(V-I)^0 + 5.29.$$ (22)

These equations define the ridge lines of the instability strip in the short- and long-wave CMDs. They are shown in Fig. 15.

Figure 15: The Galactic instability strip. Symbols are as in Fig. 11. The full lines correspond to Eqs. (21) and (22), respectively. Dashed lines indicate the adopted blue and red edges of the strip. Three outlying Cepheids are identified.

Also shown in Fig. 15 are the Cepheids with open-cluster and BBW distances from Tables 3 and 4. They define a narrow instability strip, i.e. $\pm0\hbox{$.\!\!^{\rm m}$ }13$ in (B-V)⁰ and $\pm0\hbox{$.\!\!^{\rm m}$ }10$ in (V-I)⁰. These values are upper limits considering that the observational errors are in the order of $0\hbox{$.\!\!^{\rm m}$ }2$ in absolute magnitude and at least $0\hbox{$.\!\!^{\rm m}$ }03$ in color.

   
7.2 A comparison of the instability strip position in the Galaxy, LMC, and SMC

The 314 Cepheids in LMC from Udalski et al. (1999b) and the 486 Cepheids in SMC from Udalski et al. (1999c) are shown as black dots in the M_V-(B-V)⁰ respectively (V-I)⁰ plane in Fig. 16. Some additional Cepheids, excluded by Udalski et al. on the basis of their large scatter, are shown as open symbols.

Figure 16: Comparison of the instability strip position in the Galaxy, LMC, and SMC. The dashed line is the ridge line of the instability strip of LMC and SMC from Eqs. (29-32) using the Cepheids adopted by Udalski et al. (1999a). The dotted lines are from all their fundamental-mode Cepheids. The full drawn lines are the Galactic ridge lines from Fig. 15.

To obtain mean relations defined by these Cepheids, i.e. the ridge line of the respective instability strips, we have combined the mean P-C and P-L relations of LMC and SMC.

A linear fit (cf. Sect. 3.2) over the whole period range of the good LMC Cepheids gives

   

$$(B-V)^0 = 0.363\log P + 0.270$$ (23)

$$(V-I)^0 = 0.213\log P + 0.464$$ (24)

$$M^{0}_{V} = -2.776\log P - 1.464,$$ (25)

and for SMC

   

$$(B-V)^0 = 0.361\log P + 0.234$$ (26)

$$(V-I)^0 = 0.278\log P + 0.443$$ (27)

$$M^{0}_{V} = -2.574\log P - 1.502,$$ (28)

where true moduli of $(m-M)^0_{\rm LMC}=18.54$ and $(m-M)^{0}_{\rm SMC}=19.00$ are assumed. Combining Eqs. (23-25) and (26-28) to eliminate $\log P$ yields for the instability strip ridge line equations for LMC

  

$$M^{0}_{V} = (-7.64\pm0.5)(B-V)^0 + 0.60$$ (29)

$$M^{0}_{I} = (-13.96\pm1.0)(V-I)^0 + 4.54,$$ (30)

and for SMC

  

$$M^{0}_{V} = (-7.13\pm0.5)(B-V)^0 + 0.17$$ (31)

$$M^{0}_{I} = (-10.22\pm1.0)(V-I)^0 + 2.59.$$ (32)

These mean relations are shown in Fig. 16 as dashed lines. The error of the slopes is considerable and due to the propagation of the errors of the coefficients in Eqs. (23-28). For comparison, also the ridge lines of the Galactic instability strip from Eqs. (21) and (22) are shown in Fig. 16 as a full drawn line.

In spite of the relatively large slope errors there is considerable evidence that the slopes of the instability strips [in (B-V)⁰ and (V-I)⁰] decrease from the Galaxy through LMC to SMC, i.e. with decreasing metallicity. (The one exception is the LMC slope in the (V-I)⁰ diagram which is insignificantly steeper than that of the Galaxy.) The blueward shift of the LMC and SMC Cepheids as compared to the Galaxy is manifest in all panels of Fig. 16.

If we had included also the Cepheids which Udalski et al. (1999a) have excluded (dotted lines in Fig. 16), the above conclusions would remain unchanged.

We repeat the central point made earlier, if the slope of the P-L relation for Galactic Cepheids were to be the same in some color, say in I (nearly as in Figs. 14a,b), for the Galaxy compared with that in LMC and SMC, it clearly would not be the same in B and V because of the color offsets in Fig. 16.

Figures 14a,b emphasizes the main conclusion of this paper; the P-L relations are different between the three galaxies. Figures 15 and 16 provide the clue to a possible explanation for the evident slope difference in the next section.

   
7.3 Variations in the strip boundaries in temperature translate to variations in the slopes and zero-points of the P-L relations

The differences in the positions of the observed instability strips between the Galaxy, LMC, and SMC in the color offsets at given absolute magnitudes in Fig. 16 contain the reason for the slope differences in the P-L relations in Figs. 14a,b. In the subsections that follow we first show that these differences in the P-L relations in Figs. 14a,b must be due to differences in the effective mean temperature and slopes of the ${L_{\rm bol}}$, $\log T_{\rm e}$ relations in the middle of the strip. We then show in Sect. 7.3.2 that the data in Fig. 16 show just the required slope and zero point differences in the temperatures at given absolute magnitudes. First consider the theoretical expectations.

   
7.3.1 Theoretical P-L relations in ${L_{\rm bol}}$ luminosities

The problem has been discussed in tedious detail by SBT where they investigated the effect of metallicity on the P-L relation as [Fe/H] was varied from +0.3 to -1.3. The method was brute-force straight-forward by adopting equations for the blue and red edges (for the fundamental pulsation mode) in the HR diagram as the edge equations $L(T_{\rm e},Y,Z)$. These edges were then placed in the theoretical HR diagrams $L(T_{\rm e},{\rm mass},Y,Z)$ where evolution tracks for stellar masses from 1 to 25 solar masses had been calculated for different metallicities (Z) and helium (Y) abundances by three independent groups (Geneva, Padua, and Basel).

Where these tracks enter and exit the Cepheid instability strip give mass/luminosity and temperature/luminosity relations for Cepheids. These two relations are all that are needed to enter an adopted pulsation equation, $P(L, T_{\rm e},{\rm mass},Z,Y)$, to obtain a series of P-L relations for different metallicities and helium abundances. These bolometric P-L relations were then changed to P-L relations in B, V, and I passbands by a grid of atmospheric models giving B - V and V - I colors for various $T_{\rm e}$, [Fe/H], $\log g$, and microturbulence velocities (SBT, Table 6). All of this is relevant to the present paper and can be carried over to the present problem of explaining Figs. 14a,b using the data in Fig. 16.

Consider first the pulsation equation. There is a vast literature and many versions, the later equations showing explicit dependences on the metal and helium abundances. Remarkably, most versions yield nearly identical final P-L relations. SBT tested five such equations and compared all predicted P-L relations. For the purposes of illustration in this section it is sufficient to write only one of these, that due early to van Albada & Baker (1973).

Although this equation is devised by van Albada & Baker for RR Lyrae stars, remarkably it predicts the same P-L relation to within $\pm0\hbox{$.\!\!^{\rm m}$ }1$ as the Cepheid equations of Iben & Tuggle (1975, their Eq. (3)), Chiosi et al. (1992, their Eq. (5)), and Saio & Gautschy (1998) for the chemical parameters used by SBT. The reasons for the near identical results of the equations that have a chemical dependence and those that do not are discussed in detail by SBT (their Sect. 2.4) and is of no concern here. (It comes about because of compensating trends if one assumes that Yincreases with increased Z as a result of nucleosynthesis). Our point is that the first order equation of van Albada & Baker (1973) has been shown to be entirely adequate to illustrate what we wish to show in this section.

The pulsation equation of van Albada & Baker is:

$$% \log P = 0.84 \log L - 0.68 \log {\rm Mass} - 3.48 \log T_{\rm e} + {\rm const.}$$ (33)

When we substitute a mass/luminosity relation in the second term, and a temperature/luminosity relation for the instability strip in the third term, we are left with only a period/luminosity equation. This, of course, is the bolometric period-luminosity relation.

We now ask for the slope of the predicted P-L relation, as ${\rm d}M_{\rm bol}/{\rm d}\log P$, in terms of magnitude rather than luminosity.

Let the mass/luminosity relation, derived as described above from the intersection of the evolutionary tracks with the mean of the blue and red edges in the theoretical HR diagram, be:

$$% \log {\rm Mass} = a \log L + b.$$ (34)

Let the temperature/luminosity relation of the ridge line of the instability strip in the HR diagram be:

$$% \log T_{\rm e} = c \log L + d.$$ (35)

Substituting both in Eq. (33), and converting L into magnitudes gives the slope of the P-L relation as

$$% {\rm d}M_{\rm bol}/{\rm d}\log P = -2.5 (0.84-0.68a -3.48c)^{-1}.$$ (36)

Typical values from SBT (their Tables 1-5), are a=0.30 and c=-0.04. Hence, the predicted slope in Eq. (36) is ${\rm d}M_{\rm bol}/{\rm d}\log P = -3.22$.

Because the bolometric correction to convert $M_{\rm bol}$ to M_V is zero to within $0\hbox{$.\!\!^{\rm m}$ }1$ over the temperature range we are dealing with (Table 6 of SBT), this value for the slope is nearly identical of the $M_{V}/\log P$ relation as well. Remarkably, this is the slope within the errors of Eq. (16) for the Galactic Cepheids. We are clearly on the right track.

We next inquire how variations of the constants a and c in Eqs. (34) and (35) affect the slopes in Eq. (36). Because the coefficient c on the temperature is so much stronger than the coefficient a on the mass, it is clear that temperature variations of the effective mid-point of the instability strip will be the principal cause of any slope variations between the Galaxy, LMC, and SMC in Figs. 14a,b. For example, a variation in the coefficient c from -0.04 to -0.07 changes the P-L slope from ${\rm d}M_{V}/{\rm d}\log P=-3.22$ to -2.84, in the direction that Eq. (16) differs from Eqs. (25) and (28) for the SMC. An exact correspondence could be obtained by also changing the value of a that can be found by reading Tables 1-5 of SBT for the mass/luminosity relation for different metallicities.

Hence, the next step is to determine if the color difference between the Galaxy, LMC and SMC in Fig. 16 will yield temperature differences in the slope of the respective effective luminosity/temperature relations of the respective instability strips.

   
7.3.2 Conversion of the color in Fig. 16 to temperature

We now inquire if the color shifts in Fig. 16 relative to the Galaxy of $\Delta(B-V)=0\hbox{$.\!\!^{\rm m}$ }13$ for LMC at M_V=-4 and $\Delta(B-V)=0\hbox{$.\!\!^{\rm m}$ }15$ for SMC also at M_V=-4(comparing Eq. (21) with Eqs. (29) and (31)), and $\Delta(V-I)=0\hbox{$.\!\!^{\rm m}$ }10$ for LMC and $\Delta(V-I)=0\hbox{$.\!\!^{\rm m}$ }06$ for SMC also at M_V,I=-4(comparing Eq. (22) with Eqs. (30) and (32)) can be explained by the metallicity effect alone due to decreased blanketing, or do we require an additional shift in temperature as well (toward hotter temperature for LMC and SMC relative to the Galaxy)?

Assuming [Fe/H] =-0.5 for LMC and -1.0 for SMC we can read the differences in the $T_{\rm e}$ - (B-V) and $T_{\rm e}$ - (V-I) relations at fixed $T_{\rm e}$ for different metallicities from Table 6 of SBT from their model atmosphere grids. Although there is also a $\log g$ and a microturbulence dependence, they are relatively weak.

Reading the tables at $\log g = 1.5$ and a turbulent velocity of $1.7\nobreak\mbox{$\;$ km~s$^{-1}$ }$, the result is that we can account for color shifts of not more than $0\hbox{$.\!\!^{\rm m}$ }04$ in (B-V) for [Fe/H] =-0.5 and $0\hbox{$.\!\!^{\rm m}$ }10$for [Fe/H] =-1.0. The color shift in (V-I) is only $0\hbox{$.\!\!^{\rm m}$ }04$for each of these metallicities. These expected color shifts due to blanketing are less than the observed shifts in Fig. 16 by about a factor of 2. A real temperature shift is required.

With Eqs. (21, 22, 29-32), together with Table 6 of SBT we have the machinery to calculate the effective strip $L(T_{\rm e})$equations for the Galaxy, LMC, and SMC, and thereby to calculate the c slope in Eq. (35), and therefore to determine the expected change of the P-L slope in Eq. (36) due to slope differences in Eq. (35).

Using Table 6 of SBT with $\log g = 1.5$ and turbulence of  $1.7\nobreak\mbox{$\;$ km~s$^{-1}$ }$, and using both the (B-V) and (V-I) data from the Eqs. (21, 22, 29-32), and averaging the results from the (B-V) and (V-I) data separately the results are as follows.

For the Galaxy:

$$% \log T_{\rm e} = -0.048 \log L + 3.901.$$ (37)

For LMC:

$$% \log T_{\rm e} = -0.059 \log L + 3.960.$$ (38)

For SMC:

$$% \log T_{\rm e} = -0.059 \log L + 3.953.$$ (39)

The slope differences are in the direction required by Figs. 14a,b because their effect on the P-L slope in Eq. (34) is similar to what is required by comparing Eq. (16) for the Galaxy with Eq. (25) for LMC and (28) for SMC (slopes in V of -3.14, -2.78, and -2.57 respectively), although the difference in the slopes in Eqs. (37-39) is not yet quite large enough to completely accommodate the observational requirement. However, the data in Fig. 16 with their Eqs. (29-32), although showing the obvious deviation of the slopes of the instability strips in LMC and SMC from the Galaxy, yet the determination of the exact deviation is only approximate because the data have large scatter. We discuss the premier data of a superior but smaller sample in Papers II and III on the LMC and SMC separately.

   
7.3.3 The temperature offset and absolute magnitude offset

What is clear from the excess blueness in LMC and SMC in excess to what is expected from the blanketing effect alone from the low metallicities of LMC and SMC is that there must be a temperature offset toward hotter values in LMC and SMC relative to the Galaxy. The amount at $\log L =3.5 \; (M=-4)$ from Eqs. (37-39) is $\Delta \log T_{\rm e}=0.024$ for LMC and $\Delta \log T_{\rm e}=0.017$ for SMC. These, of course translate into a zero point difference in absolute magnitude (Eq. (34)) of $0\hbox{$.\!\!^{\rm m}$ }20$ at constant P, the LMC and SMC P-L relations being brighter, again in agreement with Figs. 14a,b.

Hence, the data on colors in Fig. 16 are in qualitative agreement with the requirements of steeper slopes and brighter absolute magnitudes in the mid period range for LMC and SMC compared with the Galaxy.

These temperature shifts refer to the mid points in the HR diagram of the distribution of the Cepheids in the three galaxies in the entire instability strip which has an intrinsic width of $\Delta T_{\rm e}=0.080$. Hence, the midpoint average temperature variation of $\Delta T_{\rm e}=0.02$ amounts to only 25% of the intrinsic width. This need not be an astrophysical effect in the atmospheres of the Cepheids, but rather could be due to say the position of the red edge changing as a function of metallicity (Eq. (10) of Chiosi et al. 1992, but it changes in the opposite direction with metallicity than is required here), or variations in the filling factor of the strip with metallicity as suggested by Simon & Young (1997).

We claim nothing definitive in the discussion in this Sect. 7.3 but only that there are many factors that go into the determination of the slopes and zero points of period-luminosity relations for Cepheids. With this deeper investigation of the possibilities to explain the differences in Figs. 14a,b in slope and zero point, we are left with the impression that the last thing we should expect is now that the P-L relations from galaxy-to-galaxy should ever be the same. Our main purpose in this paper is to suggest from Figs. 14a,b that indeed they are not the same in the Galaxy, LMC, and SMC.

   
8 Cepheids as extragalactic distance indicators

The non-uniqueness of the P-L relation makes the application of Cepheids as distance indicators more complex. The different slopes of the P-L relations in the Galaxy and in LMC make it impossible to determine, for instance, the LMC distance from a Galactic calibration of the P-L relation. The situation is even worse for a period-luminosity-color (P-L-C) relation, because the difference of the P-C relations of different galaxies introduces a still wider diversity. (An additional problem of the P-L-C relation is that the slope of the constant-period lines varies with the luminosity (Saio & Gautschy 1998; see also Paper II)).

The apparently hopeless situation is alleviated in part by the fact that it could be shown that at least the dominant reason for the different P-L relations is due to metallicity differences which affects the colors of Cepheids not only by blanketing but may also be the cause of the different temperatures at constant luminosity for LMC and SMC compared with the Galaxy. This leaves, however, the necessity to find independent ways to calibrate the P-L relation in function of metallicity, and/or to determine the temperature of the ridge line of the strip.

The effect of the new P-L relations on previous Cepheid distances is complex. While distances of galaxies with roughly the metallicity of LMC remain so far unchanged (a detailed discussion is deferred to Paper II), the distances of metal-rich galaxies comparable to the Galaxy should now rather be derived from the Galactic P-L relation.

Most available Cepheid distances are based on V and Iobservations with HST. They lead to the apparent distance moduli $\mu_{V}$ and $\mu_{I}$. The true modulus is then given by

$$% \mu_0 = \frac{{\cal R}_V}{{\cal R}_V - {\cal R}_I} \mu_I - \frac{{\cal R}_I}{{\cal R}_V - {\cal R}_I} \mu_V.$$ (40)

The strength of Eq. (40) is that it can be applied to individual Cepheids in the case of variable absorption. With the values of  ${{\cal R}_V}$ and ${{\cal R}_I}$ in Sect. 5.1, appropriate for average Cepheids, the coefficients of $\mu_{I}$ and $\mu_{V}$take the values 2.48 and 1.48. Due to the color dependence of the ${\cal R}$ values (Eq. (8)) the coefficients become 2.38, 1.38 and 2.53, 1.53, respectively, for intrinsicly blue, short-period Cepheids ( $\log P = 0.4$) and red, long-period Cepheids ( $\log P=1.6$). The change of the coefficients has little effect on $\mu_0$ and the coefficients 2.48 and 1.48 are therefore adequate for all periods as long as the absorption $A_{V}\la0.5$. Equation (40) shows that the true modulus $\mu_0$ reacts to any changes of the P-L relation in I as well as in V.

A list of 31 available Cepheid distances, relevant for the calibration of the extragalactic distance scale, is given by Freedman et al. (2001). They have based their Cepheid distances on a revised P-L relation in I which is even flatter than that of Madore & Freedman (1991), and have applied a bulk correction for metallicity. The 25 metal-rich galaxies in their list with a mean metallicity of $\log\mbox{[O/H]}+12=8.91$, i.e. close to the Galaxy, should now be rather determined from the steep Galactic P-L relations in V and I. The resulting corrections depend on the median period of the Cepheids in each galaxy and amounts for the 25 galaxies to a distance increase of $0\hbox{$.\!\!^{\rm m}$ }13$ on average. This reduces their suggested value of H₀=72 to H₀=68, which, however, is still affected by bias effects of their secondary distance indicators.

More relevant for the determination of the large-scale value of H₀ are the Cepheid distances of the nine galaxies which are used to calibrate the luminosity of supernovae of type Ia (cf. Parodi et al. 2000; Saha et al. 2001; Tammann et al. 2002). The distances have been determined with the traditional P-L relations of Madore & Freedman (1991), yet adopting the zero point at $(m-M)_{\rm LMC}=18.56$. Six or seven of the nine galaxies are at least as metal-rich on average as the Galaxy. If their distances are now based on the new P-L relations of Eqs. (16) and (17), the resulting distances are only slightly larger than from the Madore & Freedman P-L relation and an adopted zero point of $(m-M)_{\rm LMC}=18.56$ (Tammann et al. 2002). Thus the value of $H_{0}=57.4\pm2.3$ remains virtually unchanged. The interesting fact is that this value is no longer based on only an adopted distance of LMC, but mainly on the distances of Galactic clusters (with the Pleiades zero point at (m-M)=5.61) and on purely physical BBW distances by Gieren et al. (1998). If the HIPPARCOS calibration of the P-L relations by Groenewegen & Oudmaijer (2000) had been included, H₀ would be decreased by only $\sim$3 percent. A detailed analysis will be given in the summary paper of the HST program for the luminosity calibration of SNe Ia.

The small effect of the P-L relations in Eqs. (16) and (17) on H₀ is due to the coincidence that the steep P-L relations of the Galaxy and the flat P-L relations of LMC cross just about at $\log P=1.4$, i.e. close to the median period of the Cepheids of the calibrating galaxies.

   
9 Conclusions

Classical Cepheids pulsating in the fundamental mode in the Galaxy, LMC, and SMC define different P-C relations in (B-V)⁰ and (V-I)⁰, LMC Cepheids being bluer than Galactic ones in both colors. SMC Cepheids are still bluer in (B-V)⁰, but redder in (V-I)⁰ than those in LMC.

The different P-C relations preclude the possibility of a universal P-L relation in B, V, and/or I. In fact the Galactic P-L relation is quite steep in all three colors as shown by 28 Cepheids with BBW distance of Gieren et al. (1998) and independently by Feast's (1999) 25 Cepheids which are members of open clusters or associations. The corresponding P-L relations in LMC, based on 650 Cepheids with standard B, V, I photometry by Udalski et al. (1999b), have a significantly flatter overall slope, - an effect which is even more pronounced in SMC (Udalski et al. 1999c). The consequence is that the Cepheids in the Clouds are brighter than their Galactic counterparts at short periods (by up to $0\hbox{$.\!\!^{\rm m}$ }5$), but somewhat fainter at long periods.

The requirement that the residuals of the Galactic P-C and P-L relations be independent of the size of the (large) color excesses E(B-V) in Fernie's (1994) system leads to a slight reduction of the published values of E(B-V) and to a calibration of the E(B-V)-absorption ratios of ${\cal R}_{B}=4.17$, ${\cal R}_{V}=3.17$, and ${\cal R}_{I}=1.89$. The values apply to Cepheids of intermediate color. ${{\cal R}_B}$varies from 4.06-4.35 for the bluest and reddest Cepheids, respectively.

As a consequence of the different P-C and P-L relations in the Galaxy and in the Clouds, the ridge line of the instability strip in the M_V - (B-V)⁰ and M_I - (V-I)⁰planes of LMC and SMC is shifted bluewards with respect to the Galaxy. It is shown that these shifts are caused by a metallicity-dependent blanketing effect as well as by intrinsic temperature differences that depend on luminosity. These effects explain at the same time the different slopes of the P-C relations of the three galaxies.

At this point it seems a justified working hypothesis to assume that the observed differences of Cepheids in the three galaxies for $\log P > 1.0$ are principally due to metallicity differences. If so, the Galactic P-L relation should be applied to metal-rich galaxies, and the LMC P-L relation to galaxies with [Fe/H] $\sim -0.5$. A finer grid of metallicities, extending also to lower metallicities, is a desideratum of the future. - However, that metallicity may not be the only parameter causing variations of the slope of the P-L relation follows from the possibly different slopes of LMC Cepheids with $\log P < 1.0$ and $\log P > 1.0$ (see the forthcoming paper II of this series).

The present large-scale value of the Hubble constant, H₀=57from SNe Ia depends on the luminosity calibration of the latter, which is provided by nine SNe Ia having occurred in galaxies whose Cepheid distances have been determined (Saha et al. 2001; Tammann et al. 2002) on the basis of the traditional flat P-L relation of Madore & Freedman (1991). Six or seven of these galaxies are as metal-rich on average as the Galaxy. Their distances should now rather be based on the steep Galactic P-L relation. Coincidentally this decreases H₀ by only a few percent because the Cepheids involved have median periods close to where the Galactic and LMC P-L relations intersect.

However, the principal difference is that the zero point of H₀ depends now only weakly on any adopted distance of LMC (through the SNe Ia in the low-metallicity galaxies NGC 5253 and IC 1613), but mainly on the Galactic P-L relation whose zero point rests on the distances of the Cepheid-bearing Galactic clusters by Feast & Walker (1987) and Feast (1999) and to equal parts on the BBW distances of Gieren et al. (1998), the latter being independent of any adopted distance.

The definitive conclusion is that the notion of a universal slope of the P-L relation cannot be maintained in the presence of metallicity and strip ridge-line temperature variations.

Acknowledgements

G. A. T. and B. R. thank the Swiss National Science Foundation for valuable support. The authors thank Dres. R. Buser, S. Kanbur, C. Ngeow, M. Samland, and A. Udalski for helpful discussions and informations as well as the referee, Dr. M. Feast, for constructive improvements.

References

 
• Baade, W., & Minkowski, R. 1937, ApJ, 86, 123 NASA ADS  
• Baraffe, I., & Alibert, Y. 2001, A&A, 371, 592 (BA) NASA ADS  
• Barnes, T. G., & Evans, D. S. 1976, MNRAS, 174, 489 NASA ADS  
• Bauer, F., Alfonso, C., Albert, J. N., et al. 1999, A&A, 348, 175 NASA ADS  
• Berdnikov, L. N., Dambis, A. K., & Voziakova, O. V. 2000, A&AS, 143, 211 NASA ADS  
• Berdnikov, L. N., Voziakova, O. V., & Ibragimov, M. A. 1995, IBVS, 4141, 1 NASA ADS  
• Bersier, D. 1996, A&A, 308, 514 NASA ADS  
• Bono, G., Caputo, F., Casellani, V., & Marconi, M. 1999, ApJ, 512, 711 NASA ADS  
• Buchler, J. R., Goupil, M. J., & Piciullo, R. 1997, ApJ, 491, L99 NASA ADS  
• Buser, R. 1978, A&A, 62, 411 NASA ADS  
• Caldwell, J. A. R., & Coulson, I. M. 1986, MNRAS, 218, 223 NASA ADS  
• Caputo, F., Marconi, M., & Musella, I. 2000, A&A, 354, 610 NASA ADS  
• Chiosi, C., Wood, P., Bertelli, G., & Bressan, A. 1992, ApJ, 387, 320 NASA ADS  
• Cioni, M.-R. L., van der Marel, R. P., Loup, C., & Habing, H. J. 2000, A&A, 359, 601 NASA ADS  
• Dean, J. F. 1981, MNRAS, 197, 779 NASA ADS  
• Dean, J. F., Warren, P. R., & Cousins, A. W. J. 1978, MNRAS, 183, 569 NASA ADS  
• Eggen, O. J. 1996, AJ, 111, 1313 NASA ADS  
• Egorova, I. A., & Kovtyukh, V. V. 2001, OAP, 14, 140 NASA ADS  
• Evans, N. R., Sasselov, D. D., & Short, C. I. 2002, ApJ, 567, 1121 NASA ADS  
• Feast, M. W. 1991, in Observational Tests of Cosmological Inflation, ed. T. Shanks et al. (Dordrecht: Kluwer), 147  
• Feast, M. W. 1999, PASP, 111, 775 NASA ADS  
• Feast, M. W., & Catchpole, R. M. 1997, MNRAS, 286, 1 NASA ADS  
• Feast, M. W., & Walker, A. R. 1987, ARA&A, 25, 345 NASA ADS  
• Fernie, J. D. 1990, ApJS, 72, 153 NASA ADS  
• Fernie, J. D. 1994, ApJ, 429, 844 NASA ADS  
• Fernie, J. D., Beattie, B., Evans, N. R., & Seager, S. 1995, IBVS, 4148 (http://ddo.astro.utoronto.ca/cepheids.html)  
• Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 NASA ADS  
• Fry, A. M., & Carney, B. W. 1997, AJ, 113, 1073 NASA ADS  
• Gascoigne, S. C. B. 1974, MNRAS, 166, 25  
• Gascoigne, S. C. B., & Kron, G. E. 1965, MNRAS, 130, 333 NASA ADS  
• Gieren, W. P., Barnes, T. G., & Moffett, T. J. 1993, ApJ, 418, 135 NASA ADS  
• Gieren, W. P., Fouqué, P., & Gómez, M. 1998, ApJ, 496, 17 NASA ADS  
• Girardi, L., & Salaris, M. 2001, MNRAS, 323, 109 NASA ADS  
• Groenewegen, M. A. T, & Oudmaijer, R. D. 2000, A&A, 356, 849 NASA ADS  
• Groenewegen, M. A. T., & Salaris, R. D. 2001, A&A, 366, 752 NASA ADS  
• Iben, I., & Tuggle, R. S. 1975, ApJ, 197, 39 NASA ADS  
• Johnson, H. 1966, in Nebulae and Interstellar Matter (Chicago: Univ. Chicago Press), ed. B. M. Middlehurst, & L. H. Aller, Chapter 5  
• Kanbur, S. M., & Ngeow, C. 2002, Poster presented at Stellar Candles for the Extragalactic Distance Scale Conference, Concepcion, Chile  
• Keller, S. C., & Wood, P. R. 2002, ApJ, 578, 144 NASA ADS  
• Kovács, G. 2000, A&A, 363, 1 NASA ADS  
• Kraft, R. P. 1961, ApJ, 134, 616 NASA ADS  
• Laney, C. D., & Stobie, R. S. 1986, MNRAS, 222, 449 NASA ADS  
• Laney, C. D., & Stobie, R. S. 1993, MNRAS, 263, 921 NASA ADS  
• Laney, C. D., & Stobie, R. S. 1994, MNRAS, 266, 441 NASA ADS  
• Laney, C. D., & Stobie, R. S. 1995, MNRAS, 274, 337 NASA ADS  
• Landolt, A. 1983, AJ, 88, 439 NASA ADS  
• Landolt, A. 1992, AJ, 104, 340 NASA ADS  
• Madore, B. F., & Freedman, W. L. 1991, PASP, 103, 933 NASA ADS  
• Makarov, V. V. 2002, AJ, 124, 3299 NASA ADS  
• Moffett, T. J., & Barnes, T. G. 1986, MNRAS, 219, 45P NASA ADS  
• Olson, B. I. 1975, PASP, 87, 349 NASA ADS  
• Panagia, N. 1999, in New Views of the Magellanic Clouds, ed. Y.-H. Chu, N. Suntzeff, J. Hesser, & D. Bohlender, IAU Symp., 190, 549  
• Parodi, B. R., Saha, A., Sandage, A., & Tammann, G. A. 2000, ApJ, 540, 634 NASA ADS  
• Parsons, S. B., & Bell, R. A. 1975, Dudley Obs. Rep., 9, 73 NASA ADS  
• Pel, J. W. 1978, A&A, 62, 75 NASA ADS  
• Pietrzynski, G., & Gieren, W. 2002, AJ, 124, 2633 NASA ADS  
• Pinsonneault, M. H., Stauffer, J., Soderblom, D. R., King, J. R., & Hanson, R. B. 1998, ApJ, 504, 170 NASA ADS  
• Romaniello, M., Salaris, M., Cassisi, S., & Panagia, N. 2000, ApJ, 530, 738 NASA ADS  
• Saha, A., Sandage, A., Tammann, G. A., et al. 2001, ApJ, 562, 314 (Paper XI) NASA ADS  
• Saio, H., & Gautschy, A. 1998, ApJ, 498, 360 NASA ADS  
• Sakai, S., Zaritsky, D., & Kennicutt, R. C. 2000, AJ, 119, 1197 NASA ADS  
• Sandage, A. 1958, ApJ, 127, 513 NASA ADS  
• Sandage, A. 1969, ApJ, 158, 1115 NASA ADS  
• Sandage, A. 1972, QJRAS, 13, 202 NASA ADS  
• Sandage, A. 1988, PASP, 100, 935 NASA ADS  
• Sandage, A. 1997, PASP, 109, 1193 NASA ADS  
• Sandage, A., Bell, R. A., & Tripicco, M. J. 1999, ApJ, 522, 250 (SBT) NASA ADS  
• Sandage, A., & Eggen, O. J. 1959, MNRAS, 119, 278 NASA ADS  
• Sandage, A., Saha, A., Tammann, G. A., Panagia, N., & Macchetto, F. D. 1992, ApJ, 401, L5  
• Sandage, A., & Tammann, G. A. 1968, ApJ, 151, 531 NASA ADS  
• Schaerer, D., Meynet, G., Maeder, A., & Schaller, G. 1993, A&AS, 98, 523 NASA ADS  
• Schlegel, D., Finkbeiner, D., & Davis, M. 1998, ApJ, 500, 525 NASA ADS  
• Schmidt-Kaler, Th. 1965, in Landoldt-Börnstein, New Series, Group VI, Vol. 1, ed. H. H. Voigt (Berlin: Springer), 298  
• Sharpless, S. 1952, ApJ, 116, 251 NASA ADS  
• Sharpless, S. 1963, in Basic Astronomical Data (Chicago: Univ. Chicago Press), ed. K. Aa. Strand, Chapter 12  
• Simon, N. R., & Lee, A. S. 1981, ApJ, 248, 291 NASA ADS  
• Simon, N. R., & Schmidt, E. G. 1976, ApJ, 205, 162 NASA ADS  
• Simon, N. R., & Young, T. S. 1997, MNRAS, 288, 267 NASA ADS  
• Stello, D., & Nissen, P. E. 2001, A&A, 374, 105 NASA ADS  
• Tammann, G. A., & Reindl, B. 2002, Ap&SS., 280, 165 NASA ADS  
• Tammann, G. A., Reindl, B., Thim, F., Saha, A., & Sandage, A. 2002, in A New Era in Cosmology, ed. T. Shanks, & N. Metcalfe, ASP Conf. Ser., 283, in press [astro-ph/0112489]  
• Turner, D. G. 1992, AJ, 104, 1865 NASA ADS  
• Turner, D. G., Billings, G. W., & Berdnikov, L. N. 2001, PASP, 113, 715 NASA ADS  
• Turner, D. G., Leonard, P. J. T., & English, D. A. 1987, AJ, 93, 368 NASA ADS  
• Turner, D. G., Mandushev, G. I., & Forbes, D. 1994, AJ, 107, 1796 NASA ADS  
• Udalski, A., Szymanski, M., Kubiak, M., et al. 1999a, AcA, 49, 201 NASA ADS  
• Udalski, A., Soszynski, I., Szymanski, M., et al. 1999b, AcA, 49, 223 NASA ADS  
• Udalski, A., Soszynski, I., Szymanski, M., et al. 1999c, AcA, 49, 437 NASA ADS  
• Udalski, A., Wyrzykowski, L., Pietrzynski, G., et al. 2001, AcA, 51, 221 NASA ADS  
• Usenko, I. A., Kovtyukh, V. V., Klochkova, V. G., & Panchuk, V. E. 2001, A&A, 376, 885 NASA ADS  
• van Albada, T. S., & Baker, N. 1973, ApJ, 185, 477 NASA ADS  
• Van Leeuwen, F., Feast, M. W., Whitelock, P. A., & Yudin, B. 1997, MNRAS, 287, 955 NASA ADS  
• Walker, A. R. 1987a, South African Astron. Obs. Circ., 11, 131 NASA ADS  
• Walker, A. R. 1987b, MNRAS, 229, 31 NASA ADS  
• Walker, A. 1999, in Post-Hipparcos cosmic candles, ed. A. Heck, & F. Caputo (Dordrecht: Kluwer), 125  
• Wallerstein, G., & Carlson, M. 1960, ApJ, 132, 276 NASA ADS  
• Whitelock, P., & Feast, M. 2000, MNRAS, 319, 759 NASA ADS  
• Wildey, R. L., Burbidge, E. M., Sandage, A. R., & Burbidge, G. R. 1962, ApJ, 135, 94 NASA ADS  
• Yakimova, N. N., Nikolov, N. S., & Ivanov, G. R. 1975, in Variable Stars and Stellar Evolution, ed. V. E. Sherwood, & L. Plaut, IAU Symp., 67, 201  
• Zaritsky, D. 1999, AJ, 118, 2824 NASA ADS