Contents

• Effect of chromospheric activity on the mean colours of late-type stars
• 1 Introduction
• 2 Results
• 3 Discussion
• 4 Conclusions
• References

A&A 404, 631-636 (2003)
DOI: 10.1051/0004-6361:20030494

Effect of chromospheric activity on the mean colours of late-type stars

II. Is (B-V)₀ also affected?

P. J. Amado

Instituto de Astrofísica de Andalucía-CSIC, Camino Bajo de Huétor 24, PO Box 3004, 18080 Granada, Spain

Received 28 October 2002 / Accepted 21 March 2003

Abstract
We confirm the existence of an "excess'' in the mean dereddened (U-B)₀ colour of active single-lined spectroscopic giants over quiescent stars of the same spectral type and find evidence for this "excess'' in (B-V)₀, although at a lower scale, when plotted against (R-I)₀. This result suggests that the use of (B-V)₀ calibrations to determine fundamental parameters or spectral types for late-type active stars should be taken with caution. Since magnetic activity is definitely involved, these and similar calibrations using (U-B)₀ and/or (B-V)₀ should not be used for the study of late-type young clusters' members or late-type pre-main sequence stars without some consideration. Instead, near-infrared colours like (R-I)₀ should be better temperature indicators for these stars.

Key words: stars: activity - stars: fundamental parameters - stars: late-type

1 Introduction

Intrinsic (dereddened) Johnson (U-B)₀ and (B-V)₀ colour indices are extensively used in stellar astrophysics to determine physical classification and parameters of stars and, from there, infer properties of our Galaxy. For example, spectral type, luminosity class and distances can be determined from multicolour photometry. Synthetic colours from theoretical model atmospheres of different spectral types and luminosities can be tested to try to fit the observed colours. Distances are determined from absolute visual magnitudes ($M_{\rm V}$) or from $M_{\rm V}$-colour calibrations. Also, groups of stars, like galactic clusters, serve as tests for probing metallicity distribution and spiral structure of the Galaxy. They provide clues on the dependence of stellar abundance distribution with time (chemical evolution) and position (chemical gradients) within the Galaxy and, therefore, on the correct model for the formation of the galactic disk.

Open cluster metallicity determination methods have made extensive use of ultraviolet (UV) excesses of observed cluster members. In a previous paper, Amado & Byrne (1997) (hereafter Paper I) studied the effect of magnetic activity on the (U-B)₀ colour of cool active dwarf, subgiant and giant stars. They demonstrated that this colour index is affected by activity, in the sense that it is bluer than for an inactive star of the same spectral type (same (B-V)₀ colour). To explain this result, they hypothesized with different causes. They came to the conclusion that the major contribution to this effect, but possibly not the only one, must come from facula-like components on the photosphere of these stars that, due to their hotter temperature, shift the (U-B)₀ colour towards the blue. This effect is seen in the mean colours of active stars, averaged over several observing epochs, which are bluer than those of an inactive star of the same (B-V)₀. However, it is not so easily observed in the light and colour curves from individual campaigns because it depends on the distribution of spots (warm and cool) over the surface of the star. Generally, an active star is redder when at its minimum brightness, in agreement with the hypothesis of cool starspots as the cause of the photometric variations. However, evidences of B-V and, more strongly, U-B colour curves anti-correlated with the V light curve have been provided for very active systems, like UX Ari and HR 1099 (Catalano et al. 1996) and MM Her (Tas et al. 1999) indicating the presence of a distribution of hot spots on the photosphere of the star.

In Paper I, we mentioned that our results might have been influenced by the stars' different metallicity which had not been taken into account. We also explained the trend seen in the (U-B)₀ "excess'' for giant stars as a contrast effect between the faculae and the cooler photosphere. This effect was more evident in the sample of giant stars probably because of the method of selection of the active and inactive samples. Stars classified as "inactive'' dwarfs where the least active stars from their respective bibliographic entries, measured either by H$\alpha$ absorption or upper limits in IUE/EUVE line fluxes (see Paper I for details). Inactive giants do not show activity indicators like filled-in or emission H whereas our inactive dwarfs do. More than half of the stars on the main sequence from spectral type M5 downwards show some evidence of activity compare to less than 10% at spectral types earlier that M3 (Hawley et al. 1999). On the contrary, only giant stars with a high rotation rate present significant signs of activity. With this, we want to stress the fact that the colour-colour locus for the coolest dwarfs could be displaced by the increased number of stars showing activity, making the effect less evident.

In order to check whether this results in (U-B)₀ could also be seen in the widely used (B-V)₀, we studied these two colours by plotting them against (R-I)₀. In the sections below, we show the results we found for active giants belonging to single-lined RS CVn binary systems.

2 Results

Figure 1: Colour-colour diagrams for giant stars. a) (U-B)0 vs. (R-I)0 locus and b) (B-V)0 vs. (R-I)0 locus. Solid circles are active single-lined binary giants and open circles are inactive giants. The solid lines are the loci from Caldwell et al (1993) and from Schmidt-Kaler (1982) and the dashed lines are from Alonso et al. (1999) ( $\rm {[Fe/H]}=0.0$).

In Fig. 1, we plot the mean (U-B)₀ and (B-V)₀ against (R-I)₀ for chromospherically active single-lined spectroscopic binaries with a giant star as the active component. The observed mean colours were obtained from the catalogue of Chromospherically Active Binary Stars (CABS) by Strassmeier et al. (1993) and corrected for interstellar extinction as described in Paper I. Briefly, stars with distances (d) below 100 pc were not corrected for interstellar extinction. Stars with d > 100 pc and $\mid\! b\!\mid\; >20^{\circ}$ were corrected with the expression from Woltjer (1975)

$$\bar{E}_{B-V}=0.06 ~ {\rm cosec}(\mid\! b\!\mid)-0.06$$

and those with d > 100 pc and $\mid\! b\!\mid\; <20^{\circ}$ were corrected with the expression from Van Herck (1965)

$$A_{v}=0.14~(1-{\rm {exp}}~(-10~d~\sin{\mid\! b\!\mid~))}/ \sin{\mid\! b\!\mid}$$

where d is in kpc. The over-plotted solid lines are the colour-colour fits to the giants empirical loci by Caldwell et al. (1993), for ( $R-I)_{0}\leq1.0$, and by Schmidt-Kaler (1982) from ( $R-I)_{0}\sim 1.0$ redwards, and the dashed lines are the intrinsic colour-colour relationships from Alonso et al. (1999) for field and globular cluster giants of $\rm {[Fe/H]}=0.0$.

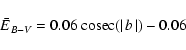
Figure 2 shows the difference between the giants' intrinsic colours linearly interpolated from the empirical loci by using (R-I)₀ for each star and the dereddened (U-B)₀ and (B-V)₀ mean colours. The sample of stars extend over a range in spectral type from G0 (( R-I)₀=0.30) to M6 (( R-I)₀=2.20) although the active giants do not extend over the full range. The active and inactive giants overlap in the range between K0 ((R-I)₀ =0.45) and K4 ((R-I)₀ =0.70).

Figure 2: (U-B)0 (upper panel) and (B-V)0 (lower panel) "anomalies'' versus (R-I)0. Colour differences computed from the loci of Caldwell et al. (1993) and Schmidt-Kaler (1982). Symbols are as in Fig. 1.

There is a positive (towards the blue) trend of increasing colour excesses in both colour indices for stars cooler than ( $R-I)_{0}\sim 0.5$, i.e., spectral type G8, and there seems to be a colour "deficiency'' for stars hotter than G8. These excesses are given in Table 1.

The excess in (U-B)₀ has an average of $0.35\pm0.26$mag. ( $0.00\pm0.11$ for the inactive stars) and the excess in (B-V)₀ is of $0.09\pm0.12$ mag. over quiescent stars of the same spectral type ( $-0.01\pm0.043$). The excess in (U-B)₀, $\delta (U-B)_{0}$, is larger when plotted against (R-I)₀ (see Fig. 2, upper panel) than when plotted against (B-V)₀ (see Fig. 2a in Paper I). This result fits in with the evidence given by the lower panel of Fig. 2 that the (B-V)₀ colour of the most active stars of spectral type later than G8 presents a positive excess towards the blue.

 

 

Table 1: Mean excesses $\bar{\delta}_{(U-B)_{0}}$ and $\bar{\delta}_{(B-V)_{0}}$, with their standard deviations, $\sigma$, for the samples of active and inactive giant stars. In the last three columns we give the maximum value for the excesses and the number of stars included in the statistics.

	$\bar{\delta}_{(U-B)_{0}}$	$\sigma$	$\bar{\delta}_{(B-V)_{0}}$	$\sigma$	$\delta_{(U-B)\rm {max}}$	$\delta_{(B-V)\rm {max}}$	n
active	+0.35	$\pm0.26$	+0.09	$\pm0.12$	+0.98	+0.38	26
inactive	+0.00	$\pm0.11$	-0.01	$\pm0.04$	+0.20	-0.11	29

3 Discussion

In Paper I, we left open the possibility that this UV excess, as we called it there (although a better designation would be Activity Blue Excess), were caused by differences in metallicity among the stars in our sample. Here we will argue against that explanation as being the only reason for the excess seen in both colours.

3.1 Metallicity

Giménez et al. (1991) found that the parameter from the Strömgren photometric system $\delta m_{1} = m_{1}(\rm {Hyades}) - m_{1}(\rm {obs})$, currently used as an indicator of stellar metallicity, was systematically deficient for the active dwarf and subgiant binaries from the CABS catalogue. This deficiency was too large to be explained in terms of metal under-abundance or evolution. In terms of the standard calibration, the observed values of $\delta m_{1}$ would have represented metal deficiencies up to -6dex in [Fe/H] with respect to the solar value, using the metal deficient star calibration by Olsen (1984) for a $\delta m_{1}$ of up to 0.3. Furthermore, they found a distinct linear relation, independent of evolution, between $\delta m_{1}$ and the colour index b-y (similar to the Johnson's B-V) in the sense of the cooler the spectral type the larger the deficiency. That linear relation is similar to the trend found here for giant stars.

Giampapa et al. (1979) compared measurements of the quiet solar photosphere and active solar regions in the uvby system showing that the effect of the active regions was to decrease the "apparent'' metal abundance derived from the m₁ index by about 35%.

Furthermore, from a uvby-$\beta$ photometric study of an X-ray sample of active late-type (F-K) stars, Morale et al. (1996) showed the presence in the sample of a star population with the photometric index c₁ typical of main-sequence stars and a deficiency in m₁ index way too large for the age of the stars in the sample (which are close to the ZAMS). They also noticed that the deviation from the standard solar-metallicity sequence for the stars in their sample had a definite colour dependence. They found that the stars with the most anomalous values of m₁ had also very high values of $f_{\rm {X}}/f_{\rm {V}}$ and X-ray surface fluxes near the "saturation'' limit observed in the most active stars and similar to the flux observed in solar active regions and in other samples of active stars. They concluded, confirming the results by Giménez et al. (1991) that activity affects Strömgren photometry indices even in non-binary systems, at least for stars redder than ( $b-y)\simeq0.450$, corresponding approximately to spectral type G8.

A strong argument confirming that the stars from Morale et al. (1996) were not metal-deficient came from Favata et al. (1997). Based on an equivalent width abundance analysis, they showed that none of the K-type stars in the sample from Morale et al. (1996) revealed any evidence for low metal abundance but, on the contrary, they all had solar or slightly super-solar abundances.

Evidences for metal abundance not being the cause for this UV excess come also from the field of open clusters, in particular from the abundance determination of the cluster NGC 2516 from its X-ray-selected members. Jeffries et al. (1997) explained the ultraviolet excess seen in the (U-B)₀, (B-V)₀ colour-colour diagram of the X-ray-selected F and G member of the cluster as a metal deficiency of [Fe/H] $~ =-0.32\pm0.06$. Later, Jeffries et al. (1998), taking into account the results in Paper I, derived, from photometry and high-resolution spectroscopy, a new value for the metallicity of NGC 2516 of $-0.1 < \rm {[Fe/H]} < 0.0$. In a recent paper, Sung et al. (2002) obtained a photometric abundance for the cluster of [Fe/H] $~=-0.10\pm0.04$ from a comparison with theoretical isochrones and found systematic bluer (U-B)₀ and (B-V)₀ colours for the X-ray bright members.

Figure 3: (U-B)0 (upper panel) and (B-V)0 (lower panel) excess versus (R-I)0. Colour differences computed from the loci of Alonso et al. (1999) ( $\rm {[Fe/H]}=0.0$). Symbols are as in Fig. 1. Two stars with uncertain extinction corrections have been removed from the plot.

On the basis of the evidences mentioned above, we rule out the possibility of metallicity as the main cause for the existence of the colour "excesses'' seen in (U-B)₀ and (B-V)₀. Different metal content in our sample of stars may contribute to the scatter seen in Fig. 2, but not to the net excess, much less up to the extent shown there, nor to the trend followed by the active giants.

3.2 Colour deficiency

 

 

Table 2: Name, spectral type, amplitude of the light curve, photometric and orbital periods and interstellar extinction correction for the stars lying below the "zero excess'' line in Fig. 2.

CABS	HD	Other	Sp.Ty.	$\Delta V$	$P_{\rm {ph}}$	$P_{\rm {orb}}$	E(U-B)	E(B-V)
				(mags.)	(days)	(days)
78	72688	VX Pyx	K0 III	0.04	19.34	45.130	0.184	0.255
85	81410	IL Hya	K1 III	0.45	12.89	12.908	0.090	0.130
86	83442	IN Vel	K2 IIIp	0.30	54.95	52.270	0.360	0.500
165	181809	V4138 Sgr	K1 III	0.35	60.23	13.048	0.110	0.160

More puzzling than the positive excess is the negative excess, or reddening, of the blue colours of the stars of spectral type hotter than G8 over quiescent stars of the same spectral type. This is seen in Fig. 2 as a "dive'' of the hotter stars under the "zero excess'' line. Next, we will try to explain this effect.

3.2.1 Interstellar extinction

Those stars in Fig. 2 below the line of "zero excess'' are the ones that needed the largest interstellar extinction corrections in our sample. One reason which could partly explain why these stars have redder (U-B)₀ and (B-V)₀ colours is that their reddening has been underestimated. In the last two columns of Table 2, we give the extinction values used in Paper I to correct these stars. They have been labelled with their CABS numbers in Fig. 2.

The star CABS 86 is in the direction of the Vela constellation, a very obscured region in the sky with a reddening of $\sim$1 mag/kpc. The distance given for this star in the CABS catalogue is of 500 pc, computed from an absolute visual magnitude $M_{\rm V}$ assumed from the spectral type. This star would need to be $\sim$170 pc further to have the intrinsic (B-V)₀ colour given by Schmidt-Kaler but, even so, it would still be too red in (U-B)₀. The Hipparcos parallax value for this star is $3.50\pm1.19$ (Perryman et al. 1997) which translate to a distance of $d=285.7\pm97.1$ pc, smaller than the one computed from $M_{\rm V}$.

The rest of the giant stars, those above the "zero excess'' line, needed very small interstellar reddening corrections, usually less than $\sim$0.1 mag, therefore we will discuss our results taking into account only these stars with small interstellar extinction correction, graphed in Fig. 3.

 

 

Table 3: Names, spectral types, colour indices at maximum brightness and total amplitudes of the long-term light curves for five stars in Fig. 2 having long-term photometry recorded.

CABS	HD	Other	Sp.Ty.	$(U-B)_{\rm {max}}$	$\Delta(U-B)$	$(B-V)_{\rm {max}}$	$\Delta(B-V)$	( $R-I)_{\rm {max}}$	$\Delta(R-I)$
50	34802	YZ Men	K1 IIIp	0.772	0.050	1.078	0.024	0.549	0.034
55	37824	V1149 Ori	K1 III	0.927	0.040	1.148	0.021	0.552	0.028
72	61245	V344 Pup	K1 III	0.788	0.059	1.035	0.034	0.496	0.024
85	81410	IL Hya	K1 III	0.712	0.056	0.997	0.064	0.512	0.040
123	136905	GX Lib	K1 III	0.705	0.057	1.026	0.037	0.526	0.032

3.2.2 Spectral type misidentification

The stars CABS 78 (VX Pyx) and CABS 85 (IL Hya) are classified in SIMBAD as dwarf stars. The CABS classifications were taken from the paper by Bidelman & MacConnell (1973). More recently, Cutispoto et al. (2001), using the Active Star Colours (ASC) method developed by Cutispoto et al. (1996), which makes use of the results of Paper I to infer spectral classification, have fitted the colours of VX Pyx, assuming binarity, with K0 III + F6 IV components. Weber & Strassmeier (1998), from spectroscopy, determined a spectral class for IL Hya of K0 III/IV and a less well defined F-G0 V/IV and Cutispoto (1998), from the colours of the star and using the ASC method, inferred a K1 III/IV. Collier et al. (1982) classified the star CABS 165 (V4138 Sgr) as a K1IV.

It is worth noting that the star CABS 53 at ( $R-I)_{0}\sim0.9$ lies exactly on the "zero excess'' line. In the ROSAT all-sky survey of active binary coronae, this star gave only upper limits in the count rate. Dempsey et al. (1997) suggested that the locus occupied by weak giants with $F_{\rm {X}}/F_{\rm {bol}}\sim10^{-6}$ on their $\log{F_{\rm {X}}}$against B-V plot might represent "marginal'' active binary systems or systems incorrectly labelled as active binary. That this star belongs to that locus and that it presents a null excess in (U-B)₀ and (B-V)₀, as can be seen in Fig. 2, suggests that it might have been incorrectly designated as an active star.

3.2.3 Empirical colour-colour loci

The fits to the giants' (U-B)₀ and (B-V)₀ versus (R-I)₀ loci were taken from the high-quality photometry of normal Pop. I stars with $R-I\leq1.0$ by Caldwell et al. (1993) and by Schmidt-Kaler (1982) for stars redder than ( $R-I)_{0}\sim 1.0$. We plot these data in Fig. 1. Since the data from Caldwell et al. (1993) were in the Cousins system, they had to be converted to the Johnson system using the transformations by Fernie (1983) and checked using the transformations given by Cousins (1981). The data converted with these two transformations agreed within the errors. However, the inactive stars with ( $R-I)_{0}\leq0.55$ in Fig. 1 also appear to lie below the line. This seems to indicate that there is a small error in the transformation from ( $R-I)_{\rm {c}}$ to ( $R-I)_{\rm {J}}$ which produces, due to the steepness of the loci in this region, a larger shift in the blue colours making the loci to appear bluer in these colours. A shift of the (U-B)₀ locus of -0.03 in (R-I)₀ at ( R-I)₀=0.4 would correct the "deficiency'' for the stars CABS 85 and CABS 165. Another possibility that we have also to bear in mind is that the colour-colour loci have an intrinsic width in (R-I)₀ which, though small, and again due to the steepness, translates to a rather large width in the blue colours.

Based on a large sample of field and globular cluster stars covering spectral types from F0 to K5, Alonso et al. (1999) tabulate intrinsic colours of giant stars derived from their $T_{\rm {eff}}$-colour calibrations in the range $3500~{\rm {K}} \le T_{\rm {eff}} \le 8000~{\rm {K}}$ for various metallicities. Their data for $\rm {[Fe/H]}=0.0$ is shown by the dashed line in Fig. 1. If this loci are used to interpolate our data, we correct the deficiency for the stars CABS 85 and 165.

Although we have tried to correct this negative excess in the sections above, we cannot rule out the possibility that, at least, part of it might be real. However, with the data used in this work, it is not possible to give a physical explanation for this effect, and a better and larger dataset is needed for such an investigation.

3.3 Effect of cool spots on the (R-I)₀ colour index

It may be argued that, the same as these active stars see their blue colours affected by hot surface inhomogeneities, their red colours might be affected by cool spots. A redward shift of the position in (R-I)₀ of active stars in the colour-colour diagrams would produce a relative excess in the blue colours with respect to those of inactive stars. In order to asses in a quantitative way this effect on the (R-I)₀ colour, we have computed some statistics on the amplitudes seen in the (R-I)₀ colour curves from a sample of active stars from Cutispoto (1998). From the amplitudes of those colour curves, mean values of $0.038\pm0.035$, $0.022\pm0.011$ and $0.019\pm0.012$ are obtained in (U-B)₀, (B-V)₀ and (R-I)₀ respectively. This means that a 3$\sigma$ value for the (R-I)₀ corresponds to 0.055 mag. This can be considered as the maximum effect (amplitude) produced in the (R-I)₀ index due to spots. In fact, the maximum observed amplitude in that sample of active star colour curves is shown by the T Tau-type star V1321 Ori with a $\Delta(R-I)=0.052$.

Furthermore, if, instead of using several single epoch colour curves, we consider the long-term variation of some of our active stars (5 star's data kindly provided by G. Cutispoto), the colours at maximum brightness can be considered as lower limits for the unspotted colours (they could even be brighter if there still existed a non-modulating component of the spot distribution on the surface of the star). The amplitude of these long-term colour curves gives us an idea of the maximum effect of spots on the colours of the stars. Those 5 active stars compose a highly homogeneous dataset because of the way they have been observed and reduced. However, for a more accurate study of the maximum effect, longer-term databases, if they exist, should be studied. For those stars, we give their long-term amplitudes (plotted also in Fig. 3 as error bars) and maximum colours in Table 3. It can be seen that the maximum effect on the (R-I)₀ colour is of $\sim$0.040 mags, with a mean value of $0.032\pm0.006$.

If, in Fig. 1, we fit the locus of (B-V)₀ vs. (R-I)₀ for the main sequence data between 0.5<(R-I)₀<0.8 with a straight line we get

(B-V)₀=1.567 (R-I)₀+0.217.

An effect on the (R-I)₀ colour of 0.055 mag translate to an effect in (B-V)₀ of 0.086 mag, not enough to explain the excess in (B-V)₀.

4 Conclusions

A clear example of the problem assessed here is that of the photometric abundance determination of the X-ray-selected members of the cluster NGC 2516. Jeffries et al. (1997) explained the ultraviolet excess as a metal deficiency for the cluster of [Fe/H] $~ =-0.32\pm0.06$. Later, Jeffries et al. (1998) derived, from photometry and high-resolution spectroscopy, a new value of $-0.1 < \rm {[Fe/H]} < 0.0$. Recently, Sung et al. (2002) obtained, from a comparison with theoretical isochrones, a photometric abundance for the cluster of [Fe/H] $~=-0.10\pm0.04$. They found systematic bluer (U-B)₀ and (B-V)₀ colours for the X-ray bright members, in the line of the results found in our present work.

By plotting the extinction corrected (U-B)₀ and (B-V)₀ mean colours of active single-lined spectroscopic binaries against (R-I)₀, we confirm the existence of a positive (towards the blue) trend of increasing colour excess in (U-B)₀, with average $0.35\pm0.26$ mag ( $0.00\pm0.11$ for the inactive stars) and find evidence for this excess in (B-V)₀ ( $0.09\pm0.12$ mag) over quiescent stars of the same spectral type ( $-0.01\pm0.04$). We find that the (U-B)₀ excess is larger when plotted against (R-I)₀ than when plotted against (B-V)₀, fitting in with the idea that this colour is also affected. We rule out metallicity as the sole explanation for this effect, being the presence of a facular component on the photosphere of the star the most probable one (see Paper I).

Therefore, we want to stress the fact that some caution should be exercised when using (B-V)₀ calibrations to determine fundamental parameters or spectral types of active late-type stars. Near-infrared colour indices should be better temperature indicators, being less affected by the excesses seen in the bluer colours. Magnitude-colour and colour-colour diagrams using one or both of these blue colours should also receive some detailed consideration when applied to young clusters and pre-main sequence late-type stars.

Acknowledgements

PJA acknowledges support at the Instituto de Astrofísica de Andalucía-CSIC by an I3P contract (I3P-PC2001-1) funded by the European Social Fund and from the program ESP2001-4528-PE. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We thank the referee, Dr. G. Cutispoto for improving this manuscript with his comments.

References

 
• Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 NASA ADS  
• Amado, P. J., & Byrne, P. B. 1997, A&A, 319, 967 NASA ADS  
• Bidelman, W. P., & MacConnell, D. J. 1973, AJ, 78, 687 NASA ADS  
• Caldwell, J. A. R., Cousins, A. W. J., Ahlers, C. C., van Wamelen, P., & Maritz, E. J. 1993, S. Afr. Astr. Obs. Circ., 15, 1 NASA ADS  
• Catalano, S., Rodonò, M., Frasca, A., & Cutispoto, G. 1996, in Stellar Surface Structure, ed. K. G. Strassmeier, & J. L. Linsky (International Astronomical Union Kluwer academic Publishers Vienna), p. 403  
• Collier, A. C., Haynes, R. F., Slee, O. B., Wright, A. E., & Hillier, D. J. 1982, MNRAS, 200, 869 NASA ADS  
• Cousins, A. W. J. 1981, S. Afr. Astr. Obs. Circ., 1, 4  
• Cutispoto, G., Messina, S., & Rodonò, M. 2001, A&AS, 367, 910  
• Cutispoto, G. 1996, A&AS, 119, 281 NASA ADS  
• Cutispoto, G. 1998, A&AS, 131, 321 NASA ADS  
• Dempsey, R. C., Linsky, J. L., Fleming, T. A., & Schmitt, J. H. M. M. 1997, ApJ, 478, 358 NASA ADS  
• Favata, F., Micela, G., Sciortino, S., & Morale, F. 1997, A&A, 324, 998 NASA ADS  
• Fernie, J. D. 1983, PASP, 95, 782 NASA ADS  
• Giampapa, M. S., Worden, S. P., & Gilliam, L. B. 1979, ApJ, 229, 1143 NASA ADS  
• Giménez, A., Reglero, V., de Castro, E., & Fernández-Figueroa, M. J. 1991, A&A, 248, 563 NASA ADS  
• Hawley, S. L., Reid, I. N., Gizis, J. E., & Byrne, P. B. 1999, in Solar and Stellar Activity: Similarities and Differences, ASP Conf. Ser., 158, 63  
• Jeffries, R. D., Thurston, M. R., & Pye, J. P. 1997, MNRAS, 287, 350 NASA ADS  
• Jeffries, R. D., James, D. J., & Thurston, M. R. 1998, MNRAS, 300, 550 NASA ADS  
• Morale, F., Micela, G., Favata, F., & Sciortino, S. 1996, A&AS, 119, 403 NASA ADS  
• Olsen, E. H. 1984, A&AS, 57, 443 NASA ADS  
• Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 NASA ADS  
• Schmidt-Kaler, T. 1982 in Landolt-Börnstein (Heidelberg: Springer), ed. K. Schaifers, & H. Voigt,  
• Strassmeier, K. G., Hall, D. S., Fekel, F. C., & Scheck, M. 1993, A&AS, 100, 173 NASA ADS  
• Sung, H., Bessell, M. S., Lee, B., & Lee, S. 2002, AJ, 123, 290 NASA ADS  
• Tas , G., Evren, S., & Ibanoglu, C. 1999, A&A, 349, 546 NASA ADS  
• Van Herck, G. 1965, Bull. Astron. Inst. Netherlands, 18, 71 NASA ADS  
• Weber, M., & Strassmeier, K. 1998, A&A, 330, 1029 NASA ADS  
• Woltjer, L. 1975, A&A, 42, 109 NASA ADS