Contents

A&A 404, 365-372 (2003)
DOI: 10.1051/0004-6361:20030474

Spectroscopic orbits of two short-period early-type binaries using two-dimensional cross-correlations[*]

J. F. González 1,2 - E. Lapasset1


1 - Complejo Astronómico El Leoncito (CASLEO), San Juan, Argentina
2 - Observatorio Astronómico de Córdoba (OAC), Argentina

Received 21 February 2003 / Accepted 24 March 2003

Abstract
We apply the two-dimensional cross-correlation technique TODCOR to derive spectroscopic orbits for the two B-type double-lined spectroscopic binaries HD 66066A and HD 315031, previously mentioned as blue straggler candidates of the open clusters NGC 2516 and NGC 6530, respectively. Reliable radial velocities for both components are measured even for orbital phases for which the separation between the spectral lines are about 0.5 times the quadratic sum of the full-width at half-maximum of the lines. Both binaries have circular orbits and the orbital periods are 1.67 and 1.38 days for HD 66066A and HD 315031, respectively. We calculate minimum masses with errors of 3-5% and obtain the projected radii from the line widths. We derive absolute stellar parameters which are consistent with the age and distance of the clusters. Both binary systems are formed by main-sequence stars and it is expected that they will experience mass-transfer between their components before the end of the core H-burning stage. HD 315031 is likely a triple system as suggested by the variation of the center-of-mass velocity.

Key words: techniques: radial velocities - binaries: spectroscopic - stars: individual: HD 66066A, HD 315031 - open clusters and associations: individual: NGC 2516, NGC 6530

1 Introduction

The discovery and orbital analysis of short-period binaries in star clusters, specially those with components having masses close to the turnoff mass, are of interest for the study of the blue straggler phenomenon because they can easily become blue stragglers as consequence of mass-transfer between the components. The spectroscopic studies of the brightest main-sequence binaries in open clusters provide not only a statistical support to the mass-transfer mechanism for the generation of blue stragglers, but also provide information about the physical properties of massive stars in open clusters. In such early-type close binary systems, however, the lines of both components appear often blended because of the rotational broadening, making the radial velocity (RV) measurements rather difficult. Fortunately, the results can be significantly improved by applying an appropriate method for the analysis of composite spectra. In the present paper we use the Two-Dimensional Cross-Correlation (TODCOR) technique developed by Zucker & Mazeh (1994), which allows to derive reliable RVs of double-lined spectra. Essentially, the object spectrum is cross-correlated simultaneously with two template spectra simulating both components. TODCOR has been successfully applied to obtain precise RVs of late-type double-lined spectroscopic binaries (Latham et al. 1996; Metcalfe et al. 1996, among others) and, more recently, for low-rotating early-type binaries (Torres et al. 2000). In the present paper we propose to use TODCOR with the aim of resolving the blended spectral lines of the two fast-rotating components of early-type close-binary systems.

Several close spectroscopic binaries have been discovered as a result of our spectroscopic program on bright main-sequence stars in open clusters (González & Lapasset 2000, 2001, 2002). In this paper we present the orbital analysis of two double-lined spectroscopic binaries (SB2), HD 66066A and HD 315031, belonging to the clusters NGC 2516 and NGC 6530, respectively. Both stars are blue straggler candidates included in Ahumada & Lapasset's (1995) catalogue, although according to recent photometric studies they may be considered as normal main-sequence stars.

HD 66066A ( $\alpha=07^{\rm h}$58$^{\rm m}$22$^{\rm s}$, $\delta=-60\hbox{$^\circ$ }51\hbox{$^\prime$ }28\hbox{$^{\prime\prime}$ }$[J2000.0]) is near the center of the open cluster NGC 2516. It was reported as a double-lined spectroscopic binary by González & Lapasset (2000). In the Color-Magnitude diagram it is located not far from the turnoff point but clearly below it, with a visual magnitude V=7.18 mag (Dachs & Kabus 1989). It is the brightest component of a visual pair with a 5  $.\!\!^{\prime\prime}$5 separation (h4031, Innes 1927). The combined light of this double star reaches 6.77 mag (Dachs & Kabus 1989), locating it close to the blue straggler region. The individual visual magnitudes tabulated in the Tycho Catalogue (ESA 1997) are 7.07 and 7.91 mag, resulting 6.66 mag for the whole system.

HD 315031 ( $\alpha=18^{\rm h}$04$^{\rm m}$28$^{\rm s}$, $\delta=-24\hbox{$^\circ$ }21\hbox{$^\prime$ }43\hbox{$^{\prime\prime}$ }$[J2000.0]) is a 8.3 mag star belonging to the open cluster NGC 6530. It was mentioned as binary by Walker (1957), according to unpublished spectroscopic observations by R. J. Trumpler. Hiltner et al. (1965) classified the spectrum of HD 315031 as B2 IV. No spectroscopic observations of this star have been reported since then. Van den Ancker et al. (1997) suggested the binarity of HD 315031 based on its abnormal position in the Color-Magnitude diagram and its high membership probability deduced from polarimetric observations.

In Sect. 2 we present our spectroscopic observations and describe the method of reduction and RV measurement. In Sect. 3 we calculate the orbital parameters while in Sect. 4 we derive absolute stellar parameters for the stellar components and discuss the physical and evolutionary status of the systems. Finally, the last section summarizes the main results.

2 Observations and radial velocity measurements

We obtained 19 and 28 echelle spectra of HD 66066A and HD 315031 respectively, between 1996 and 2002 at the Complejo Astronómico El Leoncito (CASLEO), San Juan, Argentina. We used the 2.15 m telescope and the echelle spectrograph REOSC, with a spectral resolution of 13 300. Exposure times were typically 1.5 min for HD 66066A and 8 min for HD 315031, reaching a maximum signal-to-noise ratio between 40 and 100. The depths of metallic and He I lines for these stars are of the order of 4-10% of the continuum level, resulting an effective signal-to-noise ratio of about 3-8 for the useful spectral features. As example, Fig. 1a shows two typical rectified spectra of HD 66066A.


  \begin{figure} \par\includegraphics[width=17.65cm,clip]{H4328F1.eps}\end{figure} Figure 1: Observed spectra and cross-correlation function (CCF) for the binary HD 66066A at orbital phases $\phi =0.64$ (left-hand panels) and $\phi =0.20$ (right-hand panels). a) Rectified unfiltered spectra. b) Countour plot of the 2-dim CCF. c) Sections of the 2-dim CCF passing through the maximum. These sections correspond to the right lines in b). d) Classic 1-dim CCF using a low-rotation template.

We estimated the spectral types to be B7 III + B7-8 for the binary HD 66066A, and B0.5 V + B1-2 V for HD 315031. Previous works classified the former as B8.5 III (Dachs 1972), B8.5 IV (Dachs & Kabus 1989), and B8 V (Garrison & Gray 1994), and the latter as B2 IVn (Hiltner et al. 1965). The full-width at half-maximum of the metallic lines are about 90 and 60 km s-1 for the primary and the secondary components of HD 66066A respectively, and 80 and 60 km s-1 in the case of HD 315031.


 

 
Table 1: RV of the binary HD 66066A: heliocentric Julian Date, orbital phase, RV, error and residual observed minus computed.
HJD Phase RVA $\epsilon_A$ RVB $\epsilon_B$ (O-C)A (O-C)B
-2 450 000   km s-1 km s-1 km s-1 km s-1 km s-1 km s-1
463.8009 0.9632 94.1 3.3 -57.2 4.1 -4.5 1.1
468.7480 0.9178 92.6 3.5 -51.6 3.4 1.8 -2.3
553.5168 0.5445 -40.1 4.9 113.4 6.3 4.9 3.5
554.4847 0.1226 75.2 9.5 -37.7 4.7 -4.4 -1.6
554.5076 0.1362 60.6 5.3 -37.0 4.8 -14.4 -6.3
555.5601 0.7648 21.0 6.7 24.7 5.7 -12.2 6.5
556.5543 0.3586 -23.8 4.1 84.5 3.8 -3.3 3.3
556.5797 0.3738 -22.5 3.7 88.2 4.7 3.3 0.9
834.6058 0.4202 -34.4 4.8 100.8 4.1 4.3 -1.8
835.6547 0.0466 101.2 3.3 -58.3 2.6 3.8 -1.4
835.7012 0.0744 97.0 3.7 -49.6 2.3 4.5 1.7
836.6888 0.6642 -14.2 3.2 69.3 2.9 -2.4 -1.6
837.5830 0.1982 50.6 3.0 1.0 2.3 0.6 2.5
837.7841 0.3183 -6.9 3.0 64.1 2.2 -2.3 1.6
838.6205 0.8179 55.8 3.2 -7.2 2.1 -1.3 2.4
839.6813 0.4514 -47.2 3.1 108.6 3.0 -2.7 -0.7
840.6773 0.0463 95.7 4.5 -57.4 3.1 -1.7 -0.5
950.5120 0.6432 -20.5 2.6 83.0 3.7 -0.7 2.6
955.5016 0.6231 -27.1 5.0 82.0 5.2 -0.4 -6.5



 

 
Table 2: Radial velocities of HD 315031.
HJD Phase RVA $\epsilon_A$ RVB $\epsilon_B$ $\Delta RV_A$ $\Delta RV_B$ (O-C)A (O-C)B
-2 450 000 km s-1 km s-1 km s-1 km s-1   km s-1 km s-1 km s-1 km s-1
204.7183 0.0857 66.0 3.2 -60.8 4.9 57.2 -69.7 0.5 6.4
204.8486 0.1803 33.8 3.6 -28.4 6.0 24.9 -37.2 -3.1 0.4
207.8640 0.3695 -34.7 3.4 62.1 5.7 -43.5 53.2 1.5 -7.2
552.8813 0.8475 72.5 8.6 -21.0 9.5 41.1 -52.3 3.2 -1.4
552.9017 0.8623 84.4 6.1 -22.2 11.4 53.0 -53.5 10.2 3.9
553.8515 0.5518 -33.9 5.8 114.6 8.8 -65.2 83.2 -2.7 -0.7
553.8835 0.5750 -25.6 7.0 115.9 9.0 -57.0 84.6 1.8 5.6
554.8741 0.2942 14.1 4.8 38.9 10.8 -17.2 7.5 0.9 -16.8
554.9081 0.3189 2.5 6.4 48.9 9.3 -28.9 17.5 -1.2 -19.7
555.8641 0.0129 97.5 4.9 -58.9 10.5 66.1 -90.3 0.3 -2.0
555.8888 0.0309 101.5 5.6 -55.2 9.3 70.2 -86.5 5.4 0.4
556.8429 0.7235 19.8 3.8 39.8 8.0 -11.6 8.4 -0.6 -6.3
556.8674 0.7413 28.2 7.2 31.0 15.3 -3.2 -0.4 0.4 -5.2
949.8098 0.0123 45.4 4.5 -112.9 10.1 63.7 -94.6 -2.2 -6.3
949.8523 0.0432 46.1 4.6 -109.3 10.3 64.4 -91.0 0.8 -5.7
949.9010 0.0785 40.9 4.7 -93.2 10.8 59.1 -74.9 1.0 3.1
950.8204 0.7460 -16.3 7.2 -18.8 15.3 2.0 -0.5 3.7 -2.7
955.8797 0.4190 -76.7 5.4 66.4 9.0 -58.4 84.7 -0.8 7.3
1626.9075 0.5763 -44.8 2.5 83.5 7.6 -57.8 70.5 0.8 -8.1
2444.8259 0.3742 17.5 2.6 124.9 8.2 -43.5 63.9 3.0 1.6
2444.8421 0.3860 15.9 2.6 130.4 6.7 -45.1 69.4 4.7 2.6
2445.5722 0.9160 118.9 3.1 -22.5 6.8 57.9 -83.5 0.9 -6.9
2445.6609 0.9804 127.6 2.9 -35.7 6.7 66.6 -96.7 1.1 -8.7
2445.7436 0.0405 123.7 2.9 -31.7 7.8 62.7 -92.7 -1.2 -6.9
2447.6697 0.4388 -2.0 2.9 139.0 8.4 -63.0 78.0 -1.8 -4.1
2447.7916 0.5273 -8.0 2.8 145.1 7.9 -69.0 84.1 -4.0 -3.2
2472.5138 0.4753 -30.3 3.0 120.7 7.0 -64.3 86.7 1.0 -0.8
2474.4757 0.8996 87.1 3.5 -39.7 5.2 53.2 -73.6 -0.1 -2.1


The RV measurements were carried out by means of two-dimensional correlations using observed spectra of standard stars as templates. As described in González & Lapasset (2000), we obtained template spectra for each binary component by convolving high signal-to-noise spectra of low-rotating stars of appropriate spectral-type with computed rotational profiles. In a previous step, we derived the projected rotational velocity of the components by comparing binary spectra taken at quadrature phases with the standard spectrum convolved with various rotational profiles. For the templates of both components of the binary HD 66066A we used an observed spectrum of star HR 7287 (B8 III) broadened to $v \sin i=62$ km s-1 and $v \sin i=38$ km s-1for the primary and the secondary components, respectively. In the case of HD 315031, we employed star HR 6787 (B0 V) with a rotational profile of 52 km s-1 for the primary template and HR 6165 (B2 V) with 42 km s-1 for the secondary.

RVs for both components were measured using our own version of TODCOR. Following the algorithms of Zucker & Mazeh (1994), we computed the two-dimensional cross-correlation function (CCF) from the three one-dimensional correlations involving the object and the two templates spectra. Single cross-correlations were calculated by convolving filtered spectra. The radial velocities for the two components were computed by fitting a double parabola to the correlation maximum, and their errors were derived from the asymmetric-noise, the height of the correlation peak and its width. The error computations proposed by Tonry & Davis (1979) for single cross-correlations, were applied to the sections of the CCFs parallel to the axes. In this way for each spectrum we estimated the individual error of the RV of each component.

For these RV determinations we selected spectral regions with the most conspicuous metallic or He I lines. We used the spectral windows 445.8-453.3 nm and 490.0-508.0 nm for HD 66066A, which include several lines of Fe II, Ti II, Mg II, Si II, and He I. For HD 315031, we considered the range 452.0-473.2 nm, dominated mainly by He I, Si III, and O II lines. Firstly, we applied two-dimensional cross-correlations to well resolved spectra with the aim of obtaining the luminosity-ratio of the components. The mean value resulted $0.5\pm0.1$ for HD 66066A and $0.4\pm0.1$ for HD 315031. Then, we fixed this parameter and computed the RVs of the two components for all the spectra. Tables 1 and 2 list the measured RVs.

As example, Fig. 1 shows the CCF of HD 66066A corresponding to two different orbital phases. The left-hand panels correspond to a spectrum taken closer to the quadrature while the right-hand panels are near the conjunction phase. For comparison Fig. 1d shows the classic CCF of the object spectra with the B8 III template. For this correlation we used a lower rotational profile (20 km s-1) in order to improve the resolution of the two components. In spectra where the two set of spectral lines are well resolved (left panels) the difference between the velocities obtained using TODCOR (Figs. 1b and c) and by fitting two Gaussians to the classic CCF (Fig. 1d) are generally of the same order as the measurement errors. Nevertheless, in spectra with strongly blended lines (right-hand panels) the advantage of TODCOR is clear. This technique made possible to compute reliable velocities in spectra with components separated only by 0.47 times the quadratic sum of the full-width at half-maximum of the spectral lines. In such conditions, no results were obtained by the classic method, even when in this case a lower-rotation template was used.

3 Orbital analysis

By means of a least squares fitting of the orbit, we determined the following parameters: P (period), $V_\gamma$ (center-of-mass velocity), $T_{\rm o}$ (time of maximum velocity), KA and KB (amplitudes of RV curves). The individual errors were used to assign weight to the measurements during the orbital fitting. In this first approach we adopted a point-mass model. However both binary systems are close enough for tidal and reflection effects to be important. Consequently, we computed minor corrections to the orbital parameters using one of the last versions (Wilson 1992) of the Wilson & Devinney's (1971) code in order to take into account these proximity effects. The adopted orbital parameters are listed in Tables 3 and 4 and the computed orbits are displayed, along with the observed velocities, in Figs. 2 and 3.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4328F2.eps}\end{figure} Figure 2: RV curves of HD 66066A. Circles and triangles represent the velocities of the primary and secondary, respectively. The continuous lines display the calculated radial velocities.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4328F3.eps}\end{figure} Figure 3: RV curves of HD 315031. Symbols are as in Fig. 2.

The last two columns of Tables 1 and 2 list the differences (O-C) between the observed and computed RVs. The RV residuals do not show any trend with the orbital phase but they clearly depend on the signal-to-noise ratio of the spectra. In the case of HD 66066A, for example, the rms of the residuals is 2.2 km s-1 in high signal-to-noise spectra (S/N > 70) and 5.8 km s-1 in spectra with higher noise level.

The eccentricity results indistinguishable from zero for both binaries, as it is expected as consequence of tidal friction for systems with periods as short as these. In fact, according to Zahn's (1977) theory, the circularization time-scale for these binaries is less than one million years. Consequently, we adopted a fixed value $e\equiv 0$for the computations of the remaining orbital parameters. Moreover, it can be assumed that both components rotate synchronously with the orbital motion, considering that synchronization is reached before circularization. Under this hypothesis, the relative radius of each component is proportional to the rotational broadening of its spectral lines:

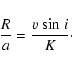
\begin{displaymath}\frac Ra = \frac{v{\rm\ sin}~i}K\cdot \end{displaymath}

In this manner, it is possible to derive the relative radii of the components from purely spectroscopic data. The resulting projected radii are listed in Tables 3 and 4, along with the remaining orbital and spectroscopic parameters.

RVs of HD 315031 showed an unusual behavior (see Table 2). The measurements from different runs are not consistent with a sole value of $V_\gamma$. We interpreted this fact as due to the presence of a third object forming a wide pair with the spectroscopic binary. So, in order to analyze the orbit of the spectroscopic system, we computed one value of $V_\gamma$ for each observing run by fitting a linear relation between RVA and RVB: ${RV}_B=V_\gamma (1+q^{-1})-q^{-1}{RV}_A$, where q is the mass-ratio. Then we calculated the difference between the observed velocities and the parameter $V_\gamma$ of the corresponding run (Cols. 7 and 8 in Table 2) and we used these data for the period searching. During the orbital analysis, the center-of-mass velocity of every observing run was considered a free parameter. Figure 3 shows the resulting RV curves.


  
Table 3: Orbital and spectroscopic parameters of HD 66066A.
\begin{displaymath}\begin{tabular}{lrcl} \hline\hline $P$ (d) & 1.67439 &$\pm$ ... ...B\sin i$ ($R_{\odot}$) &1.3 &$\pm$ &0.3 \\ \hline \end{tabular}\end{displaymath}



  
Table 4: Orbital and spectroscopic parameters of HD 315031.
\begin{displaymath}\begin{tabular}{lrcl} \hline \hline $P$ (d) &1.377436 &$\pm$&... ...n i$ ($R_{\odot}$)& 1.14 &$\pm$& 0.22 \\ \hline \end{tabular}\end{displaymath}


4 Physical parameters and evolutionary status

4.1 HD 66066A

In this section, we intend to estimate absolute values of the masses and radii of the components, and to see how do they compare to normal members of NGC 2516. From RV curves and rotational velocities, we have derived masses and radii of the components except for the factors $\sin ^3 i$ and $\sin i$, respectively. Thus, for each possible value of the orbital inclination, we are able to obtain these stellar parameters in absolute units. Figure 4 shows the Mass-Radius diagram for the possible configurations of the components of the binary HD 66066A. Being the spectroscopic mass-radius relation almost parallel to the zero-age main-sequence some insight of the evolutionary status is provided by the spectroscopic data, even if the orbital inclination is unknown. The secondary component appears to be still close to the zero-age main sequence, while the primary presents a more advanced evolutionary status, allowing a useful comparison with theoretical isochrones.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4328F4.eps}\end{figure} Figure 4: Mass-Radius diagram for the possible configurations of the components of the binary HD 66066A (solar units). For orbital inclinations in the range $i=25~\hbox{$.\!\!^\circ$ }5{-}30~\hbox{$.\!\!^\circ$ }5$ six locations of the primary (squares) and the secondary (triangles) components are plotted. Error bars are shown for the points corresponding to $i=27~\hbox{$.\!\!^\circ$ }5$. The continuous thin curves are theoretical isochrones of Girardi et al. (2000) for solar chemical composition and $\log \tau =8.05$, 8.15 and 8.30. The heavy lines represent the zero-age and terminal-age main-sequences.

From the mass-radius relation of the two components we derived the corresponding ages, temperatures, and absolute magnitudes by interpolating in the grid of stellar models of Girardi et al. (2000). The comparison of these temperature values with the observed spectral-type constraints the possible values of the orbital inclination to a quite narrow range. In fact, only those configurations in the range $i=26~\fdg2{-}28~\hbox{$.\!\!^\circ$ }6$, are compatible with temperatures between 11 200 and 13 600 K, which correspond to spectral-types B6.5-B8.5, according to the Schmidt-Kaler's (1982) calibration. Furthermore, the absolute visual magnitude interpolated in the Girardi's models for the solution corresponding to $i=27~\hbox{$.\!\!^\circ$ }5$ (Mv=-1.07 for the integrated light of the system) results in a distance modulus of 8.43 mag (8.23-8.87 mag for $i =26~\hbox{$.\!\!^\circ$ }2{-}28~\hbox{$.\!\!^\circ$ }6 $) which is in agreement with the photometric cluster distance: V-Mv = 8.53 (Dachs & Kabus 1989); 8.35 (Meynet et al. 1993); 8.12 (Sung et al. 2002). Finally, in the Mass-Radius diagram both components lie close to the isochrone $\log \tau = 8.2$, in coincidence with the accepted cluster age: $\log \tau$ = 8.15 (Meynet et al. 1993); 8.2 (Sung et al. 2002).

All the mentioned observational data let us to adopt the solution corresponding to $i = 27~ \hbox{$.\!\!^\circ$ }5 \pm 0~\hbox{$.\!\!^\circ$ }5$ as the most probable for this system within a high confidence. The uncertainty of  $\pm 0~ \hbox{$.\!\!^\circ$ }5$ is just an estimation of the range of the possible values of the inclination. The resulting stellar parameters are shown in Table 5. This solution is consistent with the spectroscopic parameters, the temperatures derived from spectral types, and the cluster age and distance. In other words, all the available observational information on HD 66066A is consistent with a binary system composed of two normal main-sequence stars, whose evolutionary status corresponds to the age of the cluster.


  
Table 5: Absolute stellar parameters of HD 66066A corresponding to an orbital inclination of $ 27~\fdg5 \pm 0~ \hbox{$.\!\!^\circ$ }5$ .
\begin{displaymath}\begin{tabular}{lrcl} \hline \hline $a$ ($R_{\odot}$) &11.6 &... ...$R_B$ ($R_{\odot}$) &2.7 &$\pm$ &0.6 \\ \hline \end{tabular} \end{displaymath}


Finally, let us make some considerations about the possibility of mass-transfer between the components and with regard to the future evolution of the system. From the spectroscopic mass-ratio q, we computed the equivalent radius of the Roche lobe for the primary star: $R_{\rm c}/a=0.393$. Adopting 11.64 $R_{\odot}$ for the separation between the components, we find a critical volume radius of 4.58 $R_{\odot}$. If the primary exceeded this size, then mass-transfer would take place towards the secondary component through the Lagrangean point L1. The pointed line in Fig. 4 gives the critical radius as function of the primary mass, computed assuming that the total mass and angular momentum are conserved. This curve is well below the terminal-age main-sequence and very close to the present radius of the primary star. Consequently, the overflow of the Roche lobe would be imminent, giving place to a case-A mass-transfer (the mass-transfer occurs during the core H-burning stage). It is not easy to assert if there is any mass-flux at present, however, being the mass-radius relation for the components compatible with normal main-sequence stars, it is probable that no significant amount of mass has been transferred yet. In any case, we can speculate that the secondary component, after accreting mass, will become a blue straggler of the cluster NGC 2516.

4.2 HD 315031

The orbital inclination of this system is probably very low, as can be deduced from a comparison of the orbital parameters with the stellar mass suggested by the spectral type of the primary component (about 12 $M_{\odot}$).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4328F5.eps}\end{figure} Figure 5: Mass-Radius diagram for the possible configurations of thecomponents of the binary HD 315031. For orbital inclinations in the range $i=16~\hbox{$.\!\!^\circ$ }5$- $20~\hbox{$.\!\!^\circ$ }5$ five locations of the primary (squares) andthe secondary (triangles) components are plotted. Error bars are shown for the points corresponding to $i=17~\hbox{$.\!\!^\circ$ }5$. The continuous thin curves are theoretical isochrones of Bertelli et al. (1994) for solar chemical composition and $\log \tau =6.6$ and 7.0. The heavy lines represent the zero-age and terminal-age main-sequences.

In Fig. 5 possible values of masses and radii of the components are shown. The solid line shows isochrones of Bertelli et al. (1994) for $\log \tau =6.6$ and 7.0. The configuration corresponding to an inclination $i=17~\hbox{$.\!\!^\circ$ }5$ is in agreement with the spectral-types and the isochrone of the cluster. The temperature of the components, interpolated from the theoretical models, are TA = 27 000 K and TB = 23 400 K, corresponding approximately to B0-1 V and B1-2 V in the Schmidt-Kaler's (1982) calibration. Adopting this value for the orbital inclination with an error of 0 $~\hbox{$.\!\!^\circ$ }$5, we computed the stellar parameters of Table 6. The total absolute magnitude of the system results Mv = -3.0. This value differs in 1 mag from the absolute magnitude derived from the cluster distance. In fact, using the photometric data of Sung et al. (2000) we obtain Mv = -4.04 for HD 315031.


  
Table 6: Absolute stellar parameters of HD 315031 corresponding to an orbital inclination of $ 17~\fdg5 \pm 0~ \hbox{$.\!\!^\circ$ }5$.
\begin{displaymath}\begin{tabular}{lccc} \hline \hline $a$ ($R_{\odot}$)& 14.1 ... ... $R_B$ ($R_{\odot}$)& 3.8 &$\pm$& 0.7 \\ \hline \end{tabular}\end{displaymath}


The volume radius of the Roche lobe is 5.9 $R_{\odot}$. We estimate that before the system reach the age $\log \tau = 7.0$, the primary star will have filled its critical lobe, giving rise to mass-transfer. This is about one half of the main-sequence life-time for a single star of that mass. Consequently, also this binary will suffer case-A mass-transfer and, in the same way as HD 66066A, it might be considered a blue straggler predecessor.

Finally, we make some considerations with regard to the third component. With the aim of inferring some physical information, we analyzed the temporal variation of the center-of-mass velocity of the spectroscopic binary. We subtracted the computed orbit of the spectroscopic binary from the observed RVs and thus we obtained the center of mass velocity for every spectrum. Then we computed a periodogram with these data founding that several periods are compatible with the observations (35  $.\!\!^{\rm d}$2, 85  $.\!\!^{\rm d}$5, 142$^{\rm d}$, 571$^{\rm d}$, and 964$^{\rm d}$ among others). All of them produce residuals smaller than 6 km s-1 and 10 km s-1 for the RV of the primary and the secondary lines, respectively. The period $P=571^{\rm d}$ gives the smaller residuals, about 3 km s-1 and 6 km s-1, respectively. Even if the period is not unambiguously defined with the present observations, the RV variations are large enough to ensure that the third body is quite massive. For several probable periods we calculated Keplerian orbits and derived the minimum-mass for the third component using the expression:

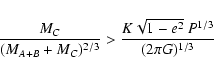
\begin{displaymath}\frac{M_C}{(M_{A+B}+M_C)^{2/3}} > \frac{K \sqrt{1-e^2} \ P^{1/3}}{(2 \pi G)^{1/3}} \end{displaymath}

where $M_{A+B} = 19.9 ~M_{\odot}$ is the total mass of the spectroscopic binary and K, e, and P are the orbital parameters computed for the center-of-mass velocity. We obtained $M_C \geq 5.8~M_{\odot}$ for the shortest period and $M_C \geq 25~M_{\odot}$ for P=571 days. Such massive star should contribute significantly to the total light of the system. This fact could explain in part the above mentioned discrepancy between the absolute magnitude of the system derived from the cluster distance modulus and the estimated value derived from the absolute stellar parameters. However, it should also be expected that the lines of this star appear in the spectrum. The absence of such spectral features in our spectrograms would favour the shortest periods as the most probable. On the other hand, some arguments could be used to understand the negative spectroscopic detection of the third star. We can speculate that, if it rotated fast, its lines could have been hidden by the observational noise and the features of the spectroscopic binary. Alternatively, if this body was also a binary or multiple star, its integrated light would result smaller than that of a single star of the same mass.

5 Summary and conclusions

We have applied the two-dimensional cross-correlation technique TODCOR to obtain spectroscopic orbits of two B-type short-period double-lined spectroscopic binaries. This technique allowed us to measure the RVs of the two components even for orbital phases for which the RV difference between the stars was about 0.5 times the quadratic sum of the full-width at half-maximum of the spectral lines of the components. Typical RV errors range from 2 to 10 km s-1, and the errors of the spectroscopic parameters were about 3-5% for the minimum masses and 1% for the projected orbital semiaxes. Assuming the synchronization of the star rotation with the orbital motion, we obtained the projected radii of the components using the rotational broadening of spectral lines. The combination of all the available observational data, i.e. orbital parameters, projected radii, spectral types, and apparent magnitude, and their comparison with theoretical stellar models, let us to estimate the orbital inclination and thus to derive absolute parameters. We estimated the uncertainties of the absolute masses to be about 6-9% and that of the absolute radii 10-20%. The obtained stellar parameters suggest that those systems are formed by two main-sequence stars whose evolutionary status agrees with the ages of their parent clusters. Although the radius of the primary component of HD 66066A is likely reaching its critical lobe, the mass-radius relation of the components do not evidence that significant mass-transfer has taken place yet.

Both binary systems are close enough to experience mass-transfer before the primary components leave the main-sequence stage. Consequently, the secondary components will increase their masses and will became blue stragglers of their clusters, as the luminosity of the cluster turnoffs diminishes due to stellar evolution. The frequency of this kind of binary stars in clusters is an important clue for evaluating the mass-transfer hypothesis as the origin of blue stragglers. Finally, we mention that both systems are triple. HD 66066A has a visual companion that could be dynamically bounded (Dachs & Kabus 1989). On the other hand, HD 315031 showed variations of the center-of-mass RVs that can be attributed to a third body forming a wide pair with the spectroscopic binary. The high amplitude of these variations suggests a mass of 6-25 $M_{\odot}$for the third component. Additional data will be collected during next observing runs in order to improve the orbital parameters of the wide system.

Acknowledgements
This work was partly supported by CONICET, ANPCYT, Secyt (UNC), and Agencia Córdoba Ciencia of Argentina.

The authors acknowledge use of the CCD and data acquisition system supported under U.S. National Science Foundation grant AST-90-15827 to R. M. Rich.

One of the spectra of HD 315031 was kindly taken by Pablo Mauas.

References


Copyright ESO 2003