Contents

A&A 404, 333-340 (2003)
DOI: 10.1051/0004-6361:20030446

Evaluating GAIA performances on eclipsing binaries

II. Orbits and stellar parameters for V781 Tau, UV Leo and GK Dra

T. Zwitter1 - U. Munari2,3 - P. M. Marrese2,4 - A. Prsa1 - E. F. Milone5 - F. Boschi2 - T. Tomov6 - A. Siviero2


1 - University of Ljubljana, Department of Physics, Jadranska 19, 1000 Ljubljana, Slovenia
2 - Osservatorio Astronomico di Padova, Sede di Asiago, 36012 Asiago (VI), Italy
3 - CISAS, Centro Interdipartimentale Studi ed Attività Spaziali dell'Università di Padova, Italy
4 - Dipartimento di Astronomia dell'Università di Padova, Osservatorio Astrofisico, 36012 Asiago (VI), Italy
5 - Physics and Astronomy Department, University of Calgary, Calgary T2N 1N4, Canada
6 - Centre for Astronomy, Nicholaus Copernicus University, ul. Gagarina 11, 87-100 Torun, Poland

Received 7 February 2003 / Accepted 18 March 2003

Abstract
The orbits and physical parameters of three close, double-lined G0 eclipsing binaries have been derived combining  $H_{\rm P}, V_{\rm T}, B_{\rm T}$ photometry from the Hipparcos/Tycho mission with 8480-8740 Å ground-based spectroscopy. The setup is mimicking the photometric and spectroscopic observations that should be obtained by GAIA. The binaries considered here are all of G0 spectral type, but each with its own complications: V781 Tau is an overcontact system with components of unequal temperature, UV Leo shows occasional surface spots and GK Dra contains a $\delta$ Scuti variable. Such peculiarities will be common among binaries to be discovered by GAIA. We find that the values of masses, radii and temperatures for such stars can be derived with a 1-2% accuracy using the adopted GAIA-like observing mode.

Key words: surveys: GAIA - stars: fundamental parameters - binaries: eclipsing - binaries: spectroscopic

1 Introduction

GAIA is a challenging Cornerstone mission re-approved by ESA last May for a lunch by around 2010. It is aimed to provide micro-arcsec astrometry, 10-band photometry and medium resolution 8480-8740 Å spectroscopy for a huge number of stars, with completeness limits for astrometry and photometry set to V=20mag. Each target star will be measured around a hundred times during the five year mission life-time, in a fashion similar to the highly successful operational mode of Hipparcos. The astrophysical and technical guidelines of the mission are described in the ESA's Concept and Technology Study (ESA SP-2000-4), in the papers by Gilmore et al. (1998) and Perryman et al. (2001), and in the proceedings of conferences devoted to GAIA and edited by Straizys (1999), Bienaymé & Turon (2002), Vansevicius et al. (2002) and Munari (2003).

In Paper I of this series, Munari et al. (2001), we have started to provide reasonable orbits for a number of new eclipsing binaries and to evaluate expected performances of GAIA on eclipsing binaries with an emphasis on the achievable accuracy of derived fundamental stellar parameters like masses and radii. The expected number of eclipsing binaries to be discovered by GAIA is $\sim$ $4 \times 10^5$. Some 105 of these will be characterized as double-lined in GAIA spectral observations. This is a huge number, many orders of magnitude larger than the total of SB2 eclipsing binaries so far investigated from ground-based observations (cf. Andersen 1991; Batten et al. 1989). Perhaps the orbits and stellar parameters could be derived from GAIA observations at a few percent error only for a few percent of them. But this still represents a two-orders of magnitude increase compared to all ground-based observing campaigns during the last century. Data obtained by GAIA should be able to provide reasonable solutions as ground-based follow-up campaigns will be very time consuming. It is therefore of great interest to investigate the expected performances of GAIA on eclipsing binaries. The purpose of this series of papers is to contribute to the fine tuning of the last details in the mission planning as well as to define the strategy to analyze the massive spectroscopic and photometric data flow on eclipsing binaries that is completely unprecedented. In the meantime, this series of papers will focus on eclipsing binaries unknown or poorly studied in the literature so far.

Paper I outlines the framework of the project and adopted methods, and the reader is referred to it (and the references therein) for details. In short, Hipparcos/Tycho photometry is adopted as a fair simulation of typical GAIA photometric data. The satellite spectroscopic data is simulated by devoted ground-based observations obtained with the Asiago 1.82 m + Echelle + CCD, set up to mimic the expected GAIA spectra. Precision of the results of our investigation can be considered as a lower limit to the accuracy obtainable from GAIA at the given source S/N, because (a) GAIA will observe in many more photometric bands than Hipparcos/Tycho and with far higher accuracy even in the narrow bands, thus both increasing light-curve mapping as well as accuracy of information on stellar temperature, limb-darkening and reddening; and (b) GAIA will acquire at least twice as many spectra per star than considered here due to obvious limitations in the telescope access time.

 

 
Table 1: Programme eclipsing binaries. Data from the Hipparcos Catalogue. $H_{\rm P}, B_{\rm T}, V_{\rm T}$ are out-of-eclipse median values.

Name		   Spct.   $H_{\rm P}$   $B_{\rm T}$   $V_{\rm T}$   $\alpha_{J2000}$   $\delta_{J2000}$ parallax         dist $\mu_\alpha$ $\mu_\delta$           
            (h m s)   ($^{\circ}$ ' '') (mas)           (pc) (mas yr-1)   (mas yr-1)    

V781 Tau		 HIP 27562 G0   8.71   9.41   8.74   05 50 13.12   +26 57 43.4   $ 12.31\pm1.35$    $\rm 81^{91}_{73}$   $-0.084 \pm 0.004$   $-0.091 \pm 0.004$

UV Leo		 HIP 52066 G0   9.20   9.78   9.00   10 38 20.77   +14 16 03.7   $10.85 \pm 1.16$    $\rm 91^{103}_{83}$   $-0.007 \pm 0.004$    $0.010 \pm 0.004$

GK Dra		 HIP 82056 G0   8.92   9.19   8.81   16 45 41.19   +68 15 30.9 $3.37 \pm 0.69$    $\rm 297^{373}_{246}$   $-0.013 \pm 0.002$    $0.014 \pm 0.002 $



 

 
Table 2: Number of Hipparcos ($H_{\rm P}$) and Tycho ($B_{\rm T}$, $V_{\rm T}$) photometric data and ground based radial velocity observations, their mean S/N and standard error for the three programme stars. Error for radial velocity is in km s-1.
    Hip   Tyc   RV
    N $\sigma$($H_{\rm P}$)   N $\sigma$($B_{\rm T}$) $\sigma$($V_{\rm T}$)   N S/N $\sigma$( RV)

V781 Tau		   61 0.014   81 0.18 0.15   41 35 8
UV Leo   96 0.015   150 0.21 0.17   29 30 10
GK Dra   124 0.017   179 0.15 0.15   35 45 3


2 Target selection

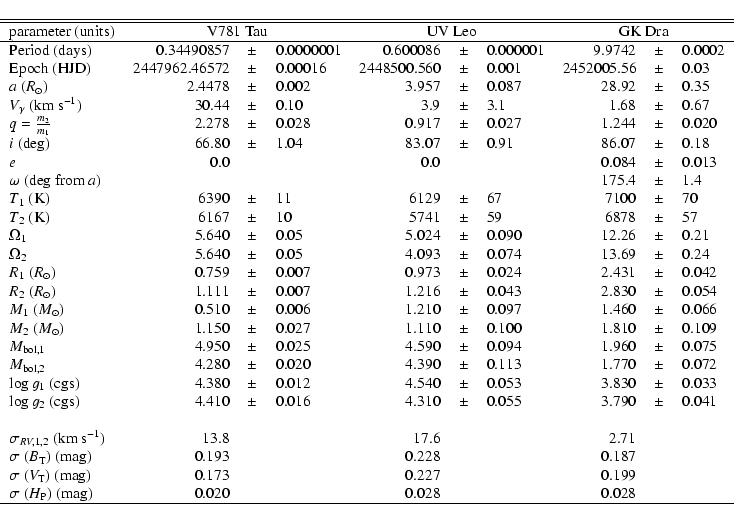
Similar to Paper I we have selected both some brand-new eclipsing binaries (i.e. without a spectroscopic or photometric orbit solution in the literature) as well as binaries with already published orbital solutions (however not in the GAIA spectral range) that can serve as an external comparison. Their basic properties are quoted in Table 1.

V781 Tau. This is a G0 over-contact ($\sim$23%) binary ( $P \sim 0.4$ days) with stars of unequal temperature. It is known to undergo period changes (Donato et al. 2003, in preparation), interpreted by Liu & Yang (2000) as shrinkage of the secondary. A spectrophotometric orbit of moderate quality has been published by Lu (1993).

UV Leo. This is a G0 short period binary (P=0.6 days) showing intrinsic variations caused by cool spots on the secondary component (cf. Mikuz et al. 2002). Orbital parameters have been derived from UBV photometric data by Frederik & Etzel (1996) and from 4430-6800 Å spectroscopic observations by Popper (1997).

GK Dra. This is a newly discovered eclipsing binary, the only existing information in the literature being BV photometric monitoring by Dallaporta et al. (2002). The authors showed that the photometric period listed in the Hipparcos Catalogue ($\sim$17 days) is wrong (the actual one being 9.97 days), and that the secondary star has intrinsic variability of a $\delta-$Sct type.


 

 
Table 3: Journal of radial velocity data. The columns give the spectrum number (as from the Asiago 1.82 m Echelle + CCD log book), the heliocentric JD, and the heliocentric radial velocities (in km s-1) for both components. An asterisk marks the spectra with a too severe blending of the lines for a meaningful measurement of radial velocities of each component. The latter have not been used in modeling of the binaries.

V781 Tau		   UV Leo   GK Dra
# HJD RV1 RV2   # HJD RV1 RV2   # HJD RV1 RV2
30731* 2451153.53313 36.4 36.4   31837 2451209.51624 -151.4 199.7   31848 2451209.60066 -71.9 59.9
30788 2451154.52849 253.0 -66.6   31878 2451210.43364 166.6 -172.8   32100 2451225.52478 74.2 -59.3
30802* 2451154.61290 23.9 23.9   31952 2451216.49289 116.0 -73.3   32775 2451274.54782 80.3 -63.4
30852 2451155.49988 207.5 -15.8   31968* 2451217.46653 18.9 18.9   32817 2451275.52285 76.5 -50.3
30867* 2451155.63872 28.9 28.9   32012 2451221.51594 -156.3 171.3   32869 2451279.53257 -70.8 67.5
30913 2451156.52626 160.1 -61.6   32085 2451225.43269 179.4 -158.2   32960 2451339.41309 -72.3 63.2
31171* 2451165.47882 53.4 53.4   32658 2451269.44151 -110.2 128.3   33115 2451402.34909 27.5 -11.0
31229* 2451166.51393 49.1 49.1   32663 2451269.47415 -149.6 175.1   33978 2451564.59894 76.9 -60.0
31278 2451167.48421 -120.6 88.9   32668 2451269.50678 -164.4 206.5   34153 2451589.57475 -79.3 63.3
31327* 2451169.58493 8.0 08.0   32802 2451275.44879 -121.7 133.1   34182 2451592.56867 50.8 -39.5
31460* 2451197.50043 -0.3 -0.3   32807 2451275.48073 -147.3 183.3   34226 2451593.57209 85.7 -63.9
31462* 2451197.51640 11.8 11.8   33967 2451564.53178 99.9 -98.0   34382 2451621.43916 5.1 5.1
31622 2451201.26374 -176.8 116.1   34228 2451593.60814 -112.1 137.0   34418 2451624.51494 72.6 -54.4
31624 2451201.28454 -152.1 104.3   34410 2451624.41908 159.9 -142.5   34453 2451625.49986 46.8 -33.2
31626* 2451201.30692 8.7 8.7   34413 2451624.46813 150.9 -177.8   34503 2451626.51482 4.5 4.5
31628* 2451201.32782 31.5 31.5   34416 2451624.49141 157.4 -128.5   35762 2451798.51275   5.2
31630* 2451201.34668 46.9 46.9   34443 2451625.42998 -102.6 141.3   36093 2451895.65844 -5.0 -5.0
31632 2451201.36542 173.6 -22.8   34501 2451626.49333 -98.4 153.7   36143 2451896.68512 -34.2 33.4
31634 2451201.38402 228.4 -52.1   36082* 2451895.53608 -31.8 -31.8   36172 2451923.62582 79.5 -56.2
31636 2451201.40272 254.7 -61.8   36084* 2451895.55506 54.9 -54.3   36286 2451924.63312 48.1 -35.8
31638 2451201.42120 265.0 -66.9   36087 2451895.60196 79.4 -91.6   36413 2451951.71656 55.3 -44.3
31640 2451201.44007 239.2 -53.0   36089 2451895.62120 106.4 -106.8   36437 2451952.52896 82.0 -62.2
31642 2451201.45878 191.9 -37.0   36095 2451895.68774 153.0 -152.5   36501 2451954.61109 46.6 -30.0
31644* 2451201.48908 42.4 42.4   36133 2451896.56836 -151.1 148.9   36533 2451955.60739 -3.8 -3.8
31646* 2451201.50783 31.5 31.5   36135 2451896.58704 -169.7 155.1   36558 2451983.57775 74.2 -55.2
31648* 2451201.52638 17.7 17.7   36140 2451896.64222 -134.7 138.5   36811 2452067.40354 -72.7 59.5
31650 2451201.54527 -143.3 99.8   36142 2451896.66113 -136.5 117.1   37930 2452300.54093 44.5 -31.4
31652 2451201.56386 -169.6 120.3   36278 2451924.52603 141.9 -178.4   37955 2452302.58732 77.8 -64.0
31654 2451201.58275 -187.5 128.3   36386 2451951.51048 156.3 -199.1   38392 2452361.47712 82.8 -63.4
31667 2451202.28749 -188.7 119.7             38394 2452361.50350 81.8 -61.8
31682 2451202.46289 265.5 -76.4             38518 2452387.46484 -80.4 69.2
34483 2451626.31285 227.7 -51.6             38536 2452388.48135 -56.8 46.4
34485 2451626.33501 259.7 -65.3             38543 2452389.49614 0.0 0.0
34487 2451626.35703 248.8 -61.0             38561 2452447.46833 -77.9 64.9
37488 2452242.53303 -181.8 121.1             38579 2452448.36282 -53.6 46.9
37497 2452242.70637 271.2 -67.4                    
37601 2452271.35705 184.5 -71.5                    
37627 2452272.38422 207.0 -61.1                    
37680* 2452277.40348 15.7 15.7                    
37821 2452280.46476 -191.9 133.3                    
38165 2452330.49815 -176.4 112.0                    



  
Table 4: Modeling solutions. The uncertainties are formal mean standard errors to the solution. The last four rows give the standard deviation of the observed points from the derived orbital solution.
\begin{displaymath}\begin{tabular}{lrclrclrcl} \hline \hline parameter (units)&\... ... &0.020 & & & 0.028 & & & 0.028 & & \\ \hline \end{tabular} \end{displaymath}



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4294F1.ps} \end{figure} Figure 1: Hipparcos $H_{\rm P}$ and Tycho $V_{\rm T}, B_{\rm T}, (B-V)_{\rm T}$ lightcurves of V781 Tau folded onto the period P = 0.34490857 days. Radial velocity measurements in the GAIA spectral interval from Table 3 are given on the top, with "+'' signs marking blended spectral lines that were not used for modeling. The curves represent the solution given in Table 4.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4294F2.ps} \end{figure} Figure 2: Hipparcos $H_{\rm P}$ and Tycho $V_{\rm T}, B_{\rm T}, (B-V)_{\rm T}$ lightcurves of UV Leo folded onto the period P = 0.600086 days. Radial velocity measurements in the GAIA spectral interval from Table 3 are given on the top, with "+'' signs marking measurements around primary eclipse that were not considered in modeling. The curves represent the solution given in Table 4.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H4294F3.ps} \end{figure} Figure 3: Hipparcos $H_{\rm P}$ and Tycho $V_{\rm T}, B_{\rm T}, (B-V)_{\rm T}$ lightcurves of GK Dra folded onto the period P = 9.9742 days. Radial velocity measurements in the GAIA spectral interval from Table 3 are given on the top. The curves represent the solution given in Table 4.

3 Observations

As explained above we use Hipparcos photometry as a lower limit to the photometric information expected from GAIA. The accuracy of Hipparcos photometry is lower, but the number of observations of each star with only a limited number of points sampling the eclipses is similar. Table 2 gives details on the number of observations of each star and their accuracy.

All spectral observations were obtained in the same mode as in Paper I, i.e. at 0.25 Å/pix dispersion and $\sim$0.50 Å resolution over the 8480-8740 Å wavelength range (therefore a resolving power $R=\lambda/\!\!\bigtriangleup\!\lambda=17~000$).

The spectroscopic observations have been collected with the Echelle + CCD spectrograph on the 1.82 m telescope operated by Osservatorio Astronomico di Padova atop of Mt. Ekar (Asiago). A 2.2 arcsec slit width was adopted to meet the resolution requirement. The detector has been a UV coated Thompson CCD with $1024\times 1024$ square pixels of 19 $\mu$m size. The GAIA spectral range is covered without gaps in a single order by the Asiago Echelle spectrograph. The actual observations however extended over a much larger wavelength interval (4550-9600 Å). Here we will limit the analysis to the GAIA spectral interval; the remaining, much larger wavelength domain will be analyzed elsewhere together with devoted multi-band photometry from ground based observations. The spectra have been extracted and calibrated in a standard fashion using IRAF software packages running on a PC under the Linux operating system. The high stability of the wavelength scale of the Asiago Echelle spectrograph has been discussed in Paper I. The results of radial velocity measurements are given in Table 3.

4 Modeling

We use an upgrade of the setup described in Paper I. The binary modeling code (Wilson 1998) was combined with van Hamme's limb darkening coefficients (van Hamme 1993), a fitting package, a graphical user interface and utilities like reddening corrections to form PHOEBE (Prsa 2003). The package is able to run on any Unix platform. It may constitute the first step toward automated solution-finding routines that will be needed to interpret the vast number of binary systems to be observed by GAIA. All results were independently derived also by the WD98K93 code (Milone et al. 1992) and WD2002 code (Kallrath et al. 1998) that are briefly described in Paper I. We found that the results are in agreement.

The usual approach to binary star modeling is to use only relative photometry obtained in each filter. Depths of eclipses in different filters constrain the ratio of the stellar temperatures, while the absolute temperature scale is tuned by judging the primary star temperature from the system colour.

In our case both stars are of similar brightness and the light curves are quite noisy. This requires some modifications to the usual approach. Hipparcos observed in three filters. The observations obtained in the broad band $H_{\rm P}$ filter have an acceptable accuracy, while those in the Tycho experiment's $B_{\rm T}$ and $V_{\rm T}$ bands are generally very noisy. We use the absolute system colours at quarter phase to fix the absolute temperature scale. The transformation between the Tycho and Johnson systems is the same as in Paper I:

$\displaystyle V_{\rm J} = V_{\rm T} - 0.090 \times (B-V)_{\rm T}$     (1)
$\displaystyle (B-V)_{\rm J} = 0.85 \times (B-V)_{\rm T}.$     (2)

Temperatures of both stars are similar, so the temperatures of the stars, T1, T2 and their radii R1, R2 are connected to the surface-weighted effective temperature of the source at quarter phase T1+2 by the relation:

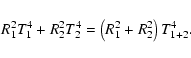\begin{displaymath}R_1^2 T_1^4 + R_2^2 T_2^4 = \left(R_1^2 + R_2^2\right) T_{1+2}^4. \end{displaymath} (3)

First the Tycho colour index at quarter phase of the model fits to the $B_{\rm T}$ and $V_{\rm T}$ light curves was transformed to the Johnson system (Eq. (2)) and the effective temperature T1+2 was determined. Modeling of the better quality $H_{\rm P}$ band observations yielded the temperature ratio and, by use of Eq. (3), also the absolute temperatures of the two stars. The process was reiterated several times to reach a self-consistent solution.

Some colour calibrations proposed recently (Bessell 2000) differ from Eq. (2) and cause effective temperature offsets of $\sim$100 K. We will comment on the changes of the results if these relations were used in the Discussion.

5 Results

Table 4 quotes the derived system parameters together with their formal errors. Table 5 compares the derived distances to the astrometric results from Hipparcos. The data and the curves from the model solutions are plotted in Figs. 1-3.

We note that model fits are generally acceptable. The differences are chiefly due to noise in the data and to some degree due to intrinsic variability of the stars. A limited number of epochs and their long timespan make modeling of transient phenomena such as stellar spots unfeasible. This will generally be also the case with data obtained by GAIA. The results were obtained assuming the stars are co-rotating. Next we discuss in turn the results for each of the objects.

5.1 V781 Tau

V781 Tau is an overcontact binary with different primary and secondary temperatures. Light curve modeling fixes the quarter phase magnitudes ( $\Phi = 0.75$) to $V_{\rm T} = 8.56$ and $B_{\rm T} = 9.16$. This corresponds to the colour index $(B-V)_{\rm T} = 0.60$ or $(B-V)_{\rm J} = 0.51$ (Eq. (2)) which gives T1+2 = 6240 K. This result was used to constrain the temperatures of the two stars through Eq. (3). Note that the magnitudes quoted in the Hipparcos catalogue (Table 1) would give somewhat different colours. However these magnitudes are just a suitable mean of all observations, also the ones close to the photometric eclipses. Therefore it is correct to use the quarter phase light curve fit and not the mean colours.

Spectroscopic observations determine absolute size of the system and individual masses as a function of the system inclination. A detailed reflection treatment was used to compute the photometric curves. The $H_{\rm P}$ light curve constrains relative sizes and temperature ratio of both stars. We found the system is actually filling its Roche lobes up to the L1 point. The stars are of unequal temperature ( $T_1 - T_2 \sim 220$ K). This difference was explained by mass transfer between the stars and the corresponding gravitational energy release (Liu & Yang 2000). A small period decrease ( ${\rm d}P/P = -5.0 \times 10^{-11}$) was also claimed to be an effect of mass transfer. We note that any mass lost from the system through the L2 point would carry away roughly twice the mean value of the specific angular momentum. Mass loss through the L2 point can therefore decrease the total angular momentum of the system, so it may be partially responsible for shortening of the orbital period. The value of the time derivative is too small to be detectable from data used in this study.

Lu (1993) published a spectrophotometric study roughly at the same accuracy level as reported in Table 4. The values of individual parameters are generally consistent, with some differences possibly arising from the simplified software he used for modeling. In particular he adopted lower effective temperatures ( T1,2 = 5950, 5861 K) but with a large error bar of 200 K. Therefore the system in his analysis turns out to be fainter and at a smaller distance (72 pc).

We note that the formal error bars on temperatures as given by the WD98 code can be increased due to systematic effects. True uncertainty can reach 100 K, increasing the uncertainty on the distance (Table 5) to 4.5% or 3.6 pc. Temperatures of both stars may be also influenced by reddening. V 781 Tau lies just $0.2^\circ$ from the galactic plane. One may expect E(B-V) = 0.09, and AV = 0.3 mag (Perry & Johnston 1982). In our calibration the effective temperature T1+2 would raise to 6540 K and the bolometric magnitude of the system would be brighter by 0.33 mag. Note that this brightening almost cancels out with the value of the total extinction. So reddening has little influence on the distance of the system reported in Table 5.

 

 
Table 5: Comparison between the Hipparcos distances and those derived from the parameters of the modeling solution in Table 4. Only formal errors quoted in Table 4 were taken into account. As explained in the text the actual distances may have a bit larger uncertainties.
  Hipparcos this paper
  (pc) (pc)

V781 Tau		 $\rm 81^{91}_{73}$ $ 81~ \pm 1.0$

UV Leo		 $\rm 91^{103}_{83}$ $ 92 \pm 6~~ $

GK Dra		 $\rm 297^{373}_{246}$ $313 \pm 14~~ $


5.2 UV Leo

UV Leo is a close binary with a pronounced spot activity that is expected to be common between G/K type binaries to be observed by GAIA. The spots cause vertical offsets in the brightness of the object on a time-scale of weeks to months (Mikuz et al. 2002). Such intrinsic variability may be contributing to the scatter of $H_{\rm P}$ observations in Fig. 2. Magnetic activity may be also responsible for part of the scatter of the radial velocity curves ( $\sigma_{RV1,2} = 17.6 $ km s-1, Table 4). In fact the Ca II lines from the secondary on JD 2 451 896 show hints of multi-component profiles, typical for spotted stars. This structure, though below the level suitable for detailed analysis in our (and usually also GAIA's) coverage of the Ca II lines, obviously increases the scatter of derived radial velocities.

The fits to the $V_{\rm T}$ and $B_{\rm T}$ curves give a quarter phase colour $(B-V)_{\rm T} = 0.72$, corresponding to $(B-V)_{\rm J} = 0.61$. This is consistent with the colours derived by Popper (1997). For main sequence stars this colour index translates into T1+2 = 5900 K. This constraint was adopted during our spectrophotometric model fitting.

Popper (1997) published a spectrophotometric solution deriving the average masses, radii and temperatures of both stars. Here we derive the parameters also for individual stars. The results are generally consistent.

5.3 GK Dra

Similar to UV Leo, GK Dra also features intrinsic variability of its components. The variability is however not caused by spots but by a likely $\delta$-Sct variability on the secondary star (Dallaporta et al. 2002). This variability has an amplitude of $\sim$0.05 mag, so it is partially responsible for the scatter in the $H_{\rm P}$ curve in Fig. 3. The $V_{\rm T}$ and $B_{\rm T}$ curves are very noisy. Still they provide an average quarter phase colour $(B-V)_{\rm T} = 0.39$, corresponding to $(B-V)_{\rm J} = 0.33$ and effective temperature T1+2 = 7000 K. The photometry to be obtained by GAIA will be of much higher accuracy ( $\sigma \sim 0.001$ mag) than Tycho observations. This will provide for accurate colour information also during eclipses and therefore constrain the temperature of either star.

Hipparcos catalogue lists an orbital period of 16.96 days. Dallaporta et al. (2002) showed by a devoted ground-based observation campaign that the true period is 9.97 days. The error in the Hipparcos results can be traced to the fact that the orbital period had to be derived from only 124 points. The system is detached so only 15 point fell into either eclipse. Spectroscopic information obtained by GAIA will greatly alleviate such problems (see Zwitter 2003 for detailed simulations). This is a consequence of the fact that every radial velocity point contributes to period determination and not only those falling into eclipses as for photometric observations.

6 Discussion

Our analysis used the Tycho to Johnson colour transformation from the Hipparcos catalogue as given in Eqs. (1) and (2). The magnitude measurements themselves were obtained from the Hipparcos and Tycho-1 epoch photometry as available through the CDS. Recently Bessell (2000) published modified calibrations that would make the $(B-V)_{\rm J}$ colours redder by 0.03 to 0.04 mag. The T1+2 temperatures for V781 Tau, UV Leo and GK Dra would be lower for 120 K, 100 K and 160 K, respectively. A modified $V_{\rm J}-V_{\rm T}$ vs. $(B-V)_{\rm T}$ relation would also make their apparent $V_{\rm J}$ magnitudes $\sim$0.01 mag brighter. Such small corrections cannot significantly modify the limb-darkening and other coefficients that depend on the absolute value of the temperature. But they do change the bolometric magnitudes and so distances. In our case the absolute bolometric magnitudes for V781 Tau, UV Leo and GK Dra would be 0.28, 0.19 and 0.46 mag fainter and the derived distances 14, 9 and 23% larger. The issue of absolute colour calibrations of the Tycho passbands does not seem to be a closed one. The new version of the Tycho catalogue (Tycho-2) quotes the old calibration (Eq. (2)) again. We therefore prefer to remain with the same calibration as used in Paper I with the possible modifications clearly spelled out.

7 Conclusions

The paper clearly demonstrates the potential of GAIA to derive accurate orbital solutions even for stars with intrinsic variability or for contact cases. GAIA will observe any object only around a hundred times. This will complicate the determination of orbital period of wide detached systems. Spectroscopic information will be particularly useful to determine the orbital period in such cases and also for a vast majority of binaries which are non-eclipsing. Spectroscopic information can be used also to derive orbital eccentricity as demonstrated by GK Dra.

Absolute scale of the system provided by spectroscopic orbit can be used to derive masses and sizes of the system components at a 1-2% level (Table 4). So these stars can be absolutely placed on an H-R diagram. Exact coevality of both stars in a binary make for a useful study of stellar isochrones. Munari (2003) discusses how additional information, like metallicity, will be obtained from the GAIA data.

The distances derived from orbital solutions compete or are superior to the Hipparcos astrometric measurements. We note that the present analysis may be influenced by uncertain calibrations in the noisy photometry obtained from the Hipparcos Tycho experiment. But for the case of GAIA the errors quoted in Table 5 are realistic, as the stellar temperatures and reddening will be known with high precision from a multi-band photometry. Note also that measurement of distances from orbital solutions, especially for overcontact binaries, is limited only by relative faintness of the objects at large distances. So hot contact binaries will be a useful tool to gauge distance throughout the Galaxy and beyond.

GAIA will be able to detect also intrinsic variability of binary components. Degree of derivable physical information depends on the nature of the variability. Stellar spots will be very common but difficult to describe. These are transient phenomena, so the star will look different on each of the 100 transits during the 5-yr mission lifetime. This can be seen also in our data. Different levels of quarter phase maxima in the V781 Tau light curve (Cereda et al. 1988) were used to claim the presence of polar spots (Lu 1993). But Hipparcos light curves do not reveal such details. Also UV Leo is an object with occasional spots that change the overall system brightness. The fact that we ignored such phenomena but still derived quite accurate orbital solutions in two systems suggests that magnetic phenomena cannot jeopardize the derivation of binary star parameters to some limit of accuracy. Other types of variability, like $\delta$-Sct variability in GK Dra (Dallaporta et al. 2002; Zwitter 2003) maintain its phase, so they will be easily detectable from GAIA data. Orbital period changes, e.g. due to passages of the third body will be quite uncommon and difficult to detect due to a limited mission lifetime.

This work reassures us of the high quality of physical information recoverable from GAIA's observations of eclipsing binaries. In future papers of this series we plan to explore more objects with intrinsic variability as well as some double lined systems with triple components.

Acknowledgements
Generous allocation of observing time with the Asiago telescopes has been vital to the present project. We would like to thank Bob Wilson who continues to provide us with the last versions of the Wilson-Devinney program and for advice on its usage. EFM acknowledges Josef Kallrath's help in further developments of spot analysis with the WD2002 code. The financial support from the Slovenian Ministry for Education, Science and Sports (to TZ and AP), of the NSERC and University of Calgary Research Grants Committee (EFM), and through the Polish KBN Grant No.5 P03D 003 20 (TT) is kindly acknowledged.

References


Copyright ESO 2003