A&A 404, 133-144 (2003)
DOI: 10.1051/0004-6361:20030435
B. W. Sohn1,2 - U. Klein2 - K.-H. Mack2,3,4
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
2 -
Radioastronomisches Institut der Universität Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
3 -
ASTRON/NFRA, Postbus 2, 7990 AA Dwingeloo, The Netherlands
4 -
Istituto di Radioastronomia del CNR, via P. Gobetti 101, 40129 Bologna,
Italy
Received 23 August 2001 / Accepted 17 March 2003
Abstract
A new intuitive tool for the analysis of synchrotron spectra is presented.
The so-called Spectral Curvature Parameter (SCP), when plotted versus
the high-frequency spectral index (
![]() )
of synchrotron
sources, provides crucial parameters on the continuum spectrum of
synchrotron radiation without the more complex modeling of spectral
ageing scenarios.
An important merit of the SCP-
)
of synchrotron
sources, provides crucial parameters on the continuum spectrum of
synchrotron radiation without the more complex modeling of spectral
ageing scenarios.
An important merit of the SCP-![]() diagram, in respect to the conventional
colour-colour diagram (i.e.
diagram, in respect to the conventional
colour-colour diagram (i.e. ![]() -
-![]() diagram), is the enhanced
reliability of extracting multiple injection spectra,
diagram), is the enhanced
reliability of extracting multiple injection spectra,
![]() .
Different from the colour-colour diagram, tracks of different
.
Different from the colour-colour diagram, tracks of different
![]() s,
especially when the synchrotron particles are young, exhibit less overlap and
less smearing in the SCP-
s,
especially when the synchrotron particles are young, exhibit less overlap and
less smearing in the SCP-![]() diagram.
Three giant radio galaxies (GRGs) and a sample of Compact steep spectrum
(CSS) souces, which are particularly suitable for
this kind of analysis, are presented.
GRGs exhibit asymmetries of their injection spectral indices
diagram.
Three giant radio galaxies (GRGs) and a sample of Compact steep spectrum
(CSS) souces, which are particularly suitable for
this kind of analysis, are presented.
GRGs exhibit asymmetries of their injection spectral indices
![]() in the SCP-
in the SCP-
![]() diagram.
The obtained
diagram.
The obtained
![]() s and the trends in the sources are
cross-checke with the literature and show remarkable confidence.
Besides the spectral steepening which is well understood in the
framework of synchrotron ageing models, spectral flattening is prominent in
the radio lobes. The spectral flattening is a clue to efficient
re-acceleration processes in the lobes. This implies that interaction with
the surrounding intergalactic or intra-cluster medium is an important
characteristic of GRGs. In the SW lobe of DA 240, there is a clear sign of CI and KP/JP bifurcation at the source extremity. This indicates a highly
relativistic energy transportation from the core or in situ acceleration
in this typical FR I lobe. Our analysis proves, if exists, KP spectra imply
the existence of strong
s and the trends in the sources are
cross-checke with the literature and show remarkable confidence.
Besides the spectral steepening which is well understood in the
framework of synchrotron ageing models, spectral flattening is prominent in
the radio lobes. The spectral flattening is a clue to efficient
re-acceleration processes in the lobes. This implies that interaction with
the surrounding intergalactic or intra-cluster medium is an important
characteristic of GRGs. In the SW lobe of DA 240, there is a clear sign of CI and KP/JP bifurcation at the source extremity. This indicates a highly
relativistic energy transportation from the core or in situ acceleration
in this typical FR I lobe. Our analysis proves, if exists, KP spectra imply
the existence of strong
![]() field with
field with
![]() .
In the CSS sources, our result confirms the CI model and
.
In the CSS sources, our result confirms the CI model and
![]() .
The synchrotron self-absorption is significant
in the CSS sample.
.
The synchrotron self-absorption is significant
in the CSS sample.
Key words: galaxies: jets - radio continuum: galaxies - methods: data analysis
Spectra of synchrotron sources from the radio to the X-ray regime reflect the energy distribution of relativistic particles, i.e. electrons whose energy distributions obey a power-law. In general, the synchrotron emissivity also follows a power-law (Pacholczyk 1970). While the conventional spectral indices only provide the spectral slope between the two observing frequencies, a multi-frequency data set can also disclose spectral curvatures over a larger frequency range. The significance of the shape of synchrotron spectra has been underlined early on by Kardashev (1962); Pacholczyk (1970); Pacholzcyk (1977); Jaffe & Perola (1973), who were among the first to describe and apply synchrotron loss models to flux densities obtained at several frequencies.
It is obvious that the information on the spectral shape of a source under
the effects of ageing, adiabatic expansion etc. provides an important tool
for understanding source evolution. If the injection of relativistic
particles following a power-law is restricted to a certain region - the
cores and/or hot spots of radio galaxies - and if the observation is
performed with appropriate resolution, one can detect regional variations of
spectral curvature by means of the above-mentioned physical processes.
Since synchrotron and Inverse Compton losses are the main energy dissipation
processes in radio galaxies, in particular at high and intermediate radio
frequencies (>1 GHz), large efforts have been made to explain the
variation of spectral curvatures - often by modeling two-frequency data -
of radio galaxies with the synchrotron ageing theory
(e.g. Alexander & Leahy 1987; Alexander 1987; Klein et al. 1995; Feretti et al. 1998;
Murgia et al. 1999). A proper determination of parameters like the injection
spectral index
![]() (the spectrum of the electron distribution
immediately after acceleration,
(the spectrum of the electron distribution
immediately after acceleration,
![]() ,
,
![]() or the break frequency
or the break frequency
![]() ,
the frequency at which spectral steepening occurs can be obtained with a
spectral ageing analysis (e.g. Carilli et al. 1991; Mack et al. 1998; Murgia et al. 1999).
This requires, however, the fitting of appropriate models with several
parameters, thus high-quality measurements at many fequencies with a good
signal-to-noise ratio are essential.
,
the frequency at which spectral steepening occurs can be obtained with a
spectral ageing analysis (e.g. Carilli et al. 1991; Mack et al. 1998; Murgia et al. 1999).
This requires, however, the fitting of appropriate models with several
parameters, thus high-quality measurements at many fequencies with a good
signal-to-noise ratio are essential.
In order to fit synchrotron and Inverse-Compton losses, three models are
widely used: The continuous injection (CI) model (Pacholczyk 1970)
assumes a mixture of electron populations of various synchrotron ages.
In this model, permanent replenishment of fresh particles is assumed so that
the injection spectral index steepens to its final value of
![]() beyond the break frequency.
The Kardashev-Pacholczyk (KP) model (Kardashev 1962; Pacholczyk 1970)
merely includes a single injection of power-law distributed electrons.
The pitch angles of the electrons are assumed to be constant with time.
The high-frequency slope in this model is
beyond the break frequency.
The Kardashev-Pacholczyk (KP) model (Kardashev 1962; Pacholczyk 1970)
merely includes a single injection of power-law distributed electrons.
The pitch angles of the electrons are assumed to be constant with time.
The high-frequency slope in this model is
![]() .
The Jaffe-Perola (JP) model (Jaffe & Perola 1973) incorporates
- similar to KP - a single injection but permits permanent pitch angle
isotropization. Beyond the break frequency this model leads to an exponential
steepening of the high-frequency spectrum. A sketch of the different tracks
of the various ageing models in the classical
.
The Jaffe-Perola (JP) model (Jaffe & Perola 1973) incorporates
- similar to KP - a single injection but permits permanent pitch angle
isotropization. Beyond the break frequency this model leads to an exponential
steepening of the high-frequency spectrum. A sketch of the different tracks
of the various ageing models in the classical
![]() space can
be found in the work of Carilli et al. (1991, see their Fig. 1).
space can
be found in the work of Carilli et al. (1991, see their Fig. 1).
In many cases the spectral ageing analysis yielded significant results. However, high-resolution multi-frequency studies of two prototypical nearby radio galaxies - 3C 449 (FR I type) by Katz-Stone & Rudnick (1997) and Cygnus A (FR II type) by Carilli et al. (1991), show trends that cannot be explained by the synchrotron ageing theory alone. The first problem is that jets and lobes (3C 449), and hot-spots and lobes (Cygnus A) have different injection spectra. The second problem to be dealt with is that of the microscopic physical conditions. While possible physical conditions such as turbulent magnetic fields and inverse-Compton scattering by cosmic microwave background photons favour the pitch-angle isotropized (JP) model, the observational results appear to support the constant pitch angle (KP) model. This could mean that the nature of the spectral curvature is more complex than expected from the synchrotron ageing theory alone.
Carilli & Barthel (1996) have pointed out the necessity of an appropriate empirical analysis that is not tied to any theoretical model in order to find the real trends in sources. Here we present a new method which can fulfill this requirement. It also aims at a quick determination of the injection spectral index and the best suited model to fit the observed spectrum. It fills the gap between the simple spectral index study and the much more complex spectral ageing analysis. It is also suited to provide first guesses of the parameters to be fit in a spectral ageing analysis, therefore making the fit procedure less susceptible to local minima in the error space.
This method is based on the so-called spectral curvature parameter (SCP).
It is defined as
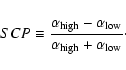
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3106F01.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg62.gif) |
Figure 1:
Schematic SCP-
|
Figure 1 illustrates the schematic tracks of the power-law spectra
undergoing synchrotron ageing. More realistic simulations of SCP-![]() diagram including the Inverse Compton equivalent field of Cosmic Microwave
Background radiation, i.e.
diagram including the Inverse Compton equivalent field of Cosmic Microwave
Background radiation, i.e.
![]() ,
are presented in what follows.
The dash-dotted curved lines represent tracks where the break frequency
has not yet reached the low-frequency regime (i.e. where
,
are presented in what follows.
The dash-dotted curved lines represent tracks where the break frequency
has not yet reached the low-frequency regime (i.e. where
![]() is
determined). The CI, KP and JP models produce different SCP ranges. This makes
it easy to distinguish between the different models in the
SCP-
is
determined). The CI, KP and JP models produce different SCP ranges. This makes
it easy to distinguish between the different models in the
SCP-
![]() plane. Different injection spectral indices also
follow different tracks.
plane. Different injection spectral indices also
follow different tracks.
Since both the CI and the KP model predict a power-law spectrum also beyond
the break frequency, namely the so-called broken power-law (Eilek & Hughes 1991),
we can calculate the maximum SCPs in these cases. For
![]() ,
these are
,
these are
![]() and
and
![]() .
In contrast, the high-frequency part of the JP model has a non-power-law
curvature, viz. an exponential one. Therefore, the tracks of JP spectra
asymptotically approach
.
In contrast, the high-frequency part of the JP model has a non-power-law
curvature, viz. an exponential one. Therefore, the tracks of JP spectra
asymptotically approach
![]() .
In any case,
.
In any case,
![]() is predicted by the JP
model only.
is predicted by the JP
model only.
An advantage of the SCP-![]() diagram with respect to the colour-colour
diagram (Katz-Stone et al. 1993), is seen when the source has multiple
diagram with respect to the colour-colour
diagram (Katz-Stone et al. 1993), is seen when the source has multiple
![]() s. As predicted in the particle ageing theory, the track of
an aged
s. As predicted in the particle ageing theory, the track of
an aged
![]() do not leave immediately the
do not leave immediately the
![]() line (see Fig. 3).
Because of the overlap of the
line (see Fig. 3).
Because of the overlap of the
![]() line and the spread of points parallel to it in the
colour-colourdiagram (hereafter C-C diagram), trends in the source can not be
easily identified. We emphasize that there are model dependent aspects
in the spectral tomography or the classical synchrotron ageing analysis,
(e.g. Alexander & Leahy 1987; Murgia et al. 1999).
line and the spread of points parallel to it in the
colour-colourdiagram (hereafter C-C diagram), trends in the source can not be
easily identified. We emphasize that there are model dependent aspects
in the spectral tomography or the classical synchrotron ageing analysis,
(e.g. Alexander & Leahy 1987; Murgia et al. 1999).
For example, the synchrotron ageing analysis can hardly achieve a
pixel-to-pixel study. The synchrotron ageing analysis is therefore done in a
way with certain subdivided integrated areas. As a property of the
integration, the obtained
![]() is strongly biased by bright
structures in these areas. The spectral tomography aimed at solving this
problem. This technique isolates from an assumed or known
is strongly biased by bright
structures in these areas. The spectral tomography aimed at solving this
problem. This technique isolates from an assumed or known
![]() component a "different'' component. The
component a "different'' component. The
![]() of this "different''
component is not directly obtained in the spectral tomography.
The spectral tomography with multiple
of this "different''
component is not directly obtained in the spectral tomography.
The spectral tomography with multiple
![]() s could be much more
complex than the classical synchrotron ageing analysis (Katz-Stone & Rudnick 1994).
The tool suggested here will extract
s could be much more
complex than the classical synchrotron ageing analysis (Katz-Stone & Rudnick 1994).
The tool suggested here will extract
![]() s without the bias due to bright structures and without
complex tomographical mapping. It can serve as a "precensor'', such as to
select the area of integration in the synchrotron ageing analysis correctly,
thus providing quite reliable physical parameters.
s without the bias due to bright structures and without
complex tomographical mapping. It can serve as a "precensor'', such as to
select the area of integration in the synchrotron ageing analysis correctly,
thus providing quite reliable physical parameters.
The clear bifurcations on the SCP-![]() diagram, between CI and KP/JP and between KP and JP, are further merits of the SCP-
diagram, between CI and KP/JP and between KP and JP, are further merits of the SCP-![]() diagram.
On the other hand, the tracks of the different models beyond the
diagram.
On the other hand, the tracks of the different models beyond the
![]() show overlaps on the C-C diagrams.
show overlaps on the C-C diagrams.
In both cases, i.e. CI and KP, straight vertical lines arise, while in the KP/JP and JP case the original curves are maintained. This fact makes the
selection of the proper ageing model easier than in the C-C diagram. Of course,
under the influence of CMB, this last argument is only true if
![]() is (much) stronger than
is (much) stronger than
![]() .
The weak point of both, the C-C diagram
and the SCP-
.
The weak point of both, the C-C diagram
and the SCP-![]() diagram is the loss of positional information of the
spectra. In order to compensate for this weakness, we present the SCP-
diagram is the loss of positional information of the
spectra. In order to compensate for this weakness, we present the SCP-![]() diagram and the SCP map together. In this way, the position information of
spectra can be restored. Some first results of this exercise will be shown in
the next section.
diagram and the SCP map together. In this way, the position information of
spectra can be restored. Some first results of this exercise will be shown in
the next section.
In this section, we present SCP-![]() diagrams of three Giant Radio
Galaxies (GRGs) and of a sample of Compact Steep Spectrum (CSS) sources. The
integrated spectra have been analyzed by Mack et al. (1998) for GRGs and by
Murgia et al. (1999) for CSS sources with synchrotron ageing models. Error
bars in the diagrams are
diagrams of three Giant Radio
Galaxies (GRGs) and of a sample of Compact Steep Spectrum (CSS) sources. The
integrated spectra have been analyzed by Mack et al. (1998) for GRGs and by
Murgia et al. (1999) for CSS sources with synchrotron ageing models. Error
bars in the diagrams are
![]() and
and
![]() .
These are
estimated as shown below,
.
These are
estimated as shown below,
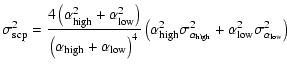 |
|||
These objects are classified by their projected linear sizes. The measurements
used here have been performed by Mack et al. (1997) at frequencies between 326 MHz and 10.6 GHz. We use four frequencies in our analysis, viz. 326 MHz,
610 MHz, 4.8 GHz and 10.6 GHz. We compute
![]() as
as
![]() ,
and
,
and
![]() as
as
![]() .
All maps were convolved to a common resolution of
.
All maps were convolved to a common resolution of
![]() ,
SCP-
,
SCP-![]() diagrams were produced for brightness levels above
diagrams were produced for brightness levels above ![]()
![]() .
In general, the low-frequency spectral indices in the lobes
of all three sources remain relatively constant,
.
In general, the low-frequency spectral indices in the lobes
of all three sources remain relatively constant,
![]() .
This means that neither ageing processes nor synchrotron
self-absorption play an important rôle at low frequencies in the regions
of interest. In what follows, we shall discuss the results for the three GRGs
investigated here in detail. For the best performance, if needed, the cubic
convolution interpolation method with a value of -0.5 is used when regridding
(Park & Schowengerdt 1983). The linear convolution interpolation shows marginal
difference.
.
This means that neither ageing processes nor synchrotron
self-absorption play an important rôle at low frequencies in the regions
of interest. In what follows, we shall discuss the results for the three GRGs
investigated here in detail. For the best performance, if needed, the cubic
convolution interpolation method with a value of -0.5 is used when regridding
(Park & Schowengerdt 1983). The linear convolution interpolation shows marginal
difference.
The radio morphology of DA 240 is symmetric at low frequencies, but becomes increasingly asymmetric towards higher frequencies (Mack et al. 1997). At 326 MHz, DA 240 is seen as a "Fat Double''. The SW fat lobe has disappeared at 10.6 GHz, forming an elongated edge-darkened FR-I-type lobe. On the contrary, the NE lobe maintains its "fat round'' shape up to 10.6 GHz.
A fit to the SCP-![]() diagram yields steep injection spectra,
diagram yields steep injection spectra,
![]() (NE lobe) and
(NE lobe) and ![]() 0.94 (SW lobe). These
unusually steep and asymmetric injection spectra have already been reported by
Mack et al. (1998), viz. 0.76 and 0.97 for the NE and SW lobe respectively.
Those authors used the synchrotron ageing technique. The difference of the
injection spectral indices is relatively large in the NE lobe, since the
region with
0.94 (SW lobe). These
unusually steep and asymmetric injection spectra have already been reported by
Mack et al. (1998), viz. 0.76 and 0.97 for the NE and SW lobe respectively.
Those authors used the synchrotron ageing technique. The difference of the
injection spectral indices is relatively large in the NE lobe, since the
region with
![]() of the NE lobe (Fig. 4) is included
in the integrated synchrotron ageing calculation. Including this
flatter-spectrum region,
of the NE lobe (Fig. 4) is included
in the integrated synchrotron ageing calculation. Including this
flatter-spectrum region,
![]() makes the
synchrotron ageing estimate uncertain. On the whole, our intuitive
rapid estimation shows good agreement with their result.
makes the
synchrotron ageing estimate uncertain. On the whole, our intuitive
rapid estimation shows good agreement with their result.
Besides this asymmetry of the injection spectral indices, the two lobes reveal
quite different trends in the diagram. The synchrotron ageing theory, the CI model and the KP/JP model, well describes the trend in the SW lobe
(Fig. 5). The CI bifurcation is detected.
On the other hand, the majority of the SCP values in the NE lobe are well below zero. This is a clear case of spectral
flattening. The remaining points with
![]() are best fitted by the CI model. In the NE lobe
are best fitted by the CI model. In the NE lobe
![]() commences with 0.5, then increases to 0.8 below
commences with 0.5, then increases to 0.8 below
![]() .
This is indicative of a non-relativistic strong shock as
discussed in the last section. Since there is no clue of KP bifurcation (see
Fig. 1) or outreach of JP spectra on the SCP-
.
This is indicative of a non-relativistic strong shock as
discussed in the last section. Since there is no clue of KP bifurcation (see
Fig. 1) or outreach of JP spectra on the SCP-![]() diagram,
due to the sensitivity limit of the observation, we can not definitely prefer
any model to the others, except for region CI mentioned in
Fig. 5.
Comparing Fig. 4 and Fig. 5,
it is found that the projected position of the CI bifurcation is the
channel of the brightness peak of the SW lobe to the SW extremity.
This possibly indicates that the physical condition of CI model, namely
continuous injected electrons with no significant escape, is yet valid in
this region.
diagram,
due to the sensitivity limit of the observation, we can not definitely prefer
any model to the others, except for region CI mentioned in
Fig. 5.
Comparing Fig. 4 and Fig. 5,
it is found that the projected position of the CI bifurcation is the
channel of the brightness peak of the SW lobe to the SW extremity.
This possibly indicates that the physical condition of CI model, namely
continuous injected electrons with no significant escape, is yet valid in
this region.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3106F04.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg83.gif) |
Figure 4:
SCP map of DA 240.
The contours show the total intensities at 326 MHz (Mack et al. 1997).
Contour levels are 3
|
![\begin{figure}
\includegraphics[width=11.5cm,clip]{H3106F05.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg84.gif) |
Figure 5:
SCP- |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{H3106F07.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg86.gif) |
Figure 7:
SCP map NGC 315.
Contours show the total intensities at 326 MHz Mack et al. (1997). Contour
levels are 3
|
Spectral flattening is present over the whole source. The value
![]() in the NW lobe is consistent with the estimate
of Mack et al. (1998), who obtained
in the NW lobe is consistent with the estimate
of Mack et al. (1998), who obtained
![]() .
On the other hand, we
cannot properly estimate the injection spectral index of the SE lobe, due to
the small number of points with
.
On the other hand, we
cannot properly estimate the injection spectral index of the SE lobe, due to
the small number of points with
![]() and the large uncertainties.
The general trend in the SE lobe
implies a steep injection spectrum,
and the large uncertainties.
The general trend in the SE lobe
implies a steep injection spectrum,
![]() .
The trends in
the two lobes are neither symmetric nor asymmetric, but rather symmetric
w.r.t the minor-axis (Fig. 7). At the southern ends
of the two lobes, the spectral-upturning is striking. After that, towards
the north, a gradual steepening follows.
.
The trends in
the two lobes are neither symmetric nor asymmetric, but rather symmetric
w.r.t the minor-axis (Fig. 7). At the southern ends
of the two lobes, the spectral-upturning is striking. After that, towards
the north, a gradual steepening follows.
The tracks of the NW and the SE lobe are well separated, which implies
different injection indices, although the error is quite large. The reason
for the extremely flat and even upturning curvature in the NW is unclear.
Unresolved background sources or relativistic shocks could be the explanation.
Enßlin et al. (2001) suggest that the relic NW tail of NGC 315 is
re-accelerated by a cosmological shock wave. Our analysis demonstrates that
the particles in both lobes have been re-accelerated. If the re-acceleration
scenario is true, the spectral flattening implies that the energy threshold of
this acceleration and/or
![]() of this region are higher than those
of the injection spectrum. Spectral flattening plus an upturn are independent
from possible missing short-spacing problems inherent to the 610 MHz WSRT data,
since it would be detectable via the Effelsberg single dish multi-frequency
observations at 2.6, 4.8 and 10.6 GHz (Mack et al. 1998) alone. However the
prominence of the points with
of this region are higher than those
of the injection spectrum. Spectral flattening plus an upturn are independent
from possible missing short-spacing problems inherent to the 610 MHz WSRT data,
since it would be detectable via the Effelsberg single dish multi-frequency
observations at 2.6, 4.8 and 10.6 GHz (Mack et al. 1998) alone. However the
prominence of the points with
![]() could be correlated with the angular
size of the 610 MHz data. It can be speculated that this is a viable
explanation for the prominence of
could be correlated with the angular
size of the 610 MHz data. It can be speculated that this is a viable
explanation for the prominence of
![]() in NGC 315, which is by far the
largest source in terms of angular size,
in NGC 315, which is by far the
largest source in terms of angular size,
![]() .
On the other hand,
a value
.
On the other hand,
a value ![]() of our SCP-
of our SCP-![]() diagram is also obtained from
single-dish 4.8 and 10.6 GHz data and shows
diagram is also obtained from
single-dish 4.8 and 10.6 GHz data and shows
![]() .
The spectral flattening in NGC 315 is mainly because of a low
.
The spectral flattening in NGC 315 is mainly because of a low
![]() .
.
This source is the largest known GRG, with
![]() Mpc. It has a typical
FR II morphology. Our value of
Mpc. It has a typical
FR II morphology. Our value of
![]() of 0.7 in the SE lobe
(Fig. 11)
is in the range of the integrated synchrotron ageing estimate of 0.5 to 0.7
by Mack et al. (1998). In the NW lobe, we obtain a steep
of 0.7 in the SE lobe
(Fig. 11)
is in the range of the integrated synchrotron ageing estimate of 0.5 to 0.7
by Mack et al. (1998). In the NW lobe, we obtain a steep
![]() of 1.10. The integrated spectral index from synchrotron ageing theory for this
lobe is 0.7.
of 1.10. The integrated spectral index from synchrotron ageing theory for this
lobe is 0.7.
The spectral flattening shown at the extremity of the SE lobe is due to a
known background source (Mack et al. 1997). In the NW lobe, we find two different values of
![]() ,
without any significant flattening. One
of them is well fitted by a steep spectrum,
,
without any significant flattening. One
of them is well fitted by a steep spectrum,
![]() .
The
trend of these data clearly
shows the synchrotron ageing in the lobe. In the backflow or so-called bridge
region,
.
The
trend of these data clearly
shows the synchrotron ageing in the lobe. In the backflow or so-called bridge
region,
![]() yields the best fit. Such an injection
discrepancy between hot-spots and lobes has been reported for Cygnus A
(Carilli et al. 1991).
The injection spectral indices of the hot spots and lobes of Cygnus A are 0.5
and 0.75, respectively. The difference
yields the best fit. Such an injection
discrepancy between hot-spots and lobes has been reported for Cygnus A
(Carilli et al. 1991).
The injection spectral indices of the hot spots and lobes of Cygnus A are 0.5
and 0.75, respectively. The difference
![]() here
is larger than in Cygnus A. In Cygnus A, the hot-spots have
here
is larger than in Cygnus A. In Cygnus A, the hot-spots have
![]() flatter than their lobes, i.e. their
backflows. 3C 236 has a steeper spectrum (
flatter than their lobes, i.e. their
backflows. 3C 236 has a steeper spectrum (
![]() )
in the advancing
region. An explanation for this
)
in the advancing
region. An explanation for this
![]() discrepancy
(Carilli & Barthel 1996) has not been found so far.
discrepancy
(Carilli & Barthel 1996) has not been found so far.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{H3106F10.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg97.gif) |
Figure 10:
SCP map of 3C 236.
The contours show the total intensities at 326 MHz Mack et al. (1997).
Contour levels are 3
|
![\begin{figure}
\par\includegraphics[width=11cm,clip]{H3106F12.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg99.gif) |
Figure 12: C-C diagram of 3C 236 (see Fig. 6). |
SCP-![]() diagrams can also be used for the analysis of samples of sources
for which only integrated flux densities are given. As an example we present
the application of our method to a sample of 47 Compact Steep Spectrum (CSS) sources. Murgia et al. (1999) who have analyzed the flux densities of a sample
of CSS sources in a profound synchrotron ageing study show that these sources
have moderate spectral steepening, i.e. a difference of
diagrams can also be used for the analysis of samples of sources
for which only integrated flux densities are given. As an example we present
the application of our method to a sample of 47 Compact Steep Spectrum (CSS) sources. Murgia et al. (1999) who have analyzed the flux densities of a sample
of CSS sources in a profound synchrotron ageing study show that these sources
have moderate spectral steepening, i.e. a difference of
![]() between low- and high-frequency spectral indices, which is predicted by the
continuous injection model (CI). We have used this sample to test the SCP performance, which provides an alternative method for a quick analysis of
synchrotron spectra. In essence, four frequencies 408(327) MHz, 1.4 GHz, 4.9(5.0) GHz and 10.7(10.6, 8.1) GHz, were used. When no data were available at
these frequencies, the total intensity at the frequencies given above in the
brackets were taken.
between low- and high-frequency spectral indices, which is predicted by the
continuous injection model (CI). We have used this sample to test the SCP performance, which provides an alternative method for a quick analysis of
synchrotron spectra. In essence, four frequencies 408(327) MHz, 1.4 GHz, 4.9(5.0) GHz and 10.7(10.6, 8.1) GHz, were used. When no data were available at
these frequencies, the total intensity at the frequencies given above in the
brackets were taken.
The points are found in the region where
![]() does not exceed
does not exceed
![]() .
The obtained range of
.
The obtained range of
![]() values is
rather wide. This confirms the results of Murgia et al. (1999). The fact that
values is
rather wide. This confirms the results of Murgia et al. (1999). The fact that
![]() s shows more scatter in the SCP-
s shows more scatter in the SCP-![]() analysis than in
the synchrotron model estimation is due the effect synchrotron self-absorption.
There is a clear trend that the sources with stronger
analysis than in
the synchrotron model estimation is due the effect synchrotron self-absorption.
There is a clear trend that the sources with stronger
![]() and with
smaller projected sizes have flatter
and with
smaller projected sizes have flatter
![]() .
These are the compact
GHz-Peaked Spectrum (GPS) source candidates, since due to their extreme
compactness
.
These are the compact
GHz-Peaked Spectrum (GPS) source candidates, since due to their extreme
compactness
![]() ,
synchrotron self-absorption is liekly to be
effective. The sample does not shows any correlation with redshift. This
implies that the intrinsic magnetic fields proponder by far over the magnetic
field equivalent to the cosmic microwave background.
,
synchrotron self-absorption is liekly to be
effective. The sample does not shows any correlation with redshift. This
implies that the intrinsic magnetic fields proponder by far over the magnetic
field equivalent to the cosmic microwave background.
The above analysis implies that all studied sources have a complex history.
Now we discuss some possibilities. Before attempting any physical
interpretation, we check again whether
![]() could be generated by
the possible missing short-spacing at 610 MHz. If anything, the possible
missing short spacing at 610 MHz will steepen our
could be generated by
the possible missing short-spacing at 610 MHz. If anything, the possible
missing short spacing at 610 MHz will steepen our
![]() ,
which is
already >0. Then,
,
which is
already >0. Then,
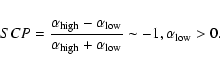
At low frequencies, there are also other physical processes that give rise to
spectral curvature, such as spectral turn-overs by synchrotron self-absorption
in regions of high particle densities, or by a low-energy cut-off in the
particle distribution. In the SCP-
![]() plane
(Fig. 2), the low-frequency turn-over produces
plane
(Fig. 2), the low-frequency turn-over produces
![]() ,
which
cannot be produced by any ageing processes. Strong self-absorption can even
produce
,
which
cannot be produced by any ageing processes. Strong self-absorption can even
produce
![]() and will be important in the central core regions,
if
and will be important in the central core regions,
if
![]() .
Since
.
Since
![]() will
eventually approach - 5/2 in the Rayleigh-Jeans limit, this will be possible.
will
eventually approach - 5/2 in the Rayleigh-Jeans limit, this will be possible.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H3106F13.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg109.gif) |
Figure 13:
SCP- |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H3106F14.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg110.gif) |
Figure 14:
Filled circles are CSS sources with
z < 0.5. Open triangles are CSS sources with
|
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H3106F15.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg115.gif) |
Figure 15:
Filled circles are CSS sources with
|
All three GRGs exhibit spectral flattening in some parts. In particular,
NGC 315 even shows signs of a spectral up-turn at high frequencies, and the
majority of SCP points is under 0. Let us consider the case where the
power-law injection spectrum is already established,
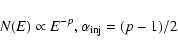
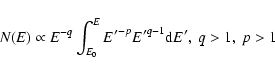
Since GRGs are extraordinary extended, they should have a weak magnetic field
![]()
![]() (Mack et al. 1998) and/or undergo re-acceleration processes
during in their lifetime.
(Mack et al. 1998) and/or undergo re-acceleration processes
during in their lifetime.
Considering the confusion of spectra of different components with different spectral indices the observed high frequency spectral flattening indicates that the flatter spectrum component is younger and secondary, i.e. re-accelerated. Otherwise we would not see the high frequency flattening, if the flatter spectrum component is as old as the steeper spectrum component. Or if the flatter spectrum component is dominant, then we would see only the flatter spectrum component in the radio frequency range and then there would be no spectral flattening.
The magnetic field
![]() and the equivalent field of the cosmic microwave
background,
and the equivalent field of the cosmic microwave
background,
![]() determine the curvature beyond
determine the curvature beyond
![]() .
In some
models (e.g. Eilek & Arendt 1996) magnetic fields produce a power-law spectrum
when they are ordered in a power-law form. However, we restrict our discussion
to the curvature beyond
.
In some
models (e.g. Eilek & Arendt 1996) magnetic fields produce a power-law spectrum
when they are ordered in a power-law form. However, we restrict our discussion
to the curvature beyond
![]() ,
and to a simple homogeneous magnetic field
,
and to a simple homogeneous magnetic field
![]() plus
plus
![]() .
Many radio galaxies as well as GRGs have weak
magnetic fields (Feretti et al. 1998; Mack et al. 1998; Parma et al. 1999), assuming that the
equipartition estimation yields the strength of the magnetic field of the
radiation region,
.
Many radio galaxies as well as GRGs have weak
magnetic fields (Feretti et al. 1998; Mack et al. 1998; Parma et al. 1999), assuming that the
equipartition estimation yields the strength of the magnetic field of the
radiation region,
![]() .
The JP model becomes more appealing
since it allows for pitch angle isotropization on a much shorter time scale than
the radiation lifetime,
.
The JP model becomes more appealing
since it allows for pitch angle isotropization on a much shorter time scale than
the radiation lifetime,
![]() .
However, KP "like''
spectra are observed (e.g. Carilli et al. 1991). In order to explain such KP
spectra, variable
.
However, KP "like''
spectra are observed (e.g. Carilli et al. 1991). In order to explain such KP
spectra, variable
![]() fields were introduced
(Tribble 1993; Eilek et al. 1997).
In Tribble's model, the magnetic field has a Maxwellian distribution, while
in Eilek's model, magnetic fields are filamented, therefore have approximately
two components,
fields were introduced
(Tribble 1993; Eilek et al. 1997).
In Tribble's model, the magnetic field has a Maxwellian distribution, while
in Eilek's model, magnetic fields are filamented, therefore have approximately
two components,
![]() and
and
![]() .
But again, any of these models
requires that some portion of their B fields is stronger than the equivalent
.
But again, any of these models
requires that some portion of their B fields is stronger than the equivalent
![]() to such as to produce the KP-like spectrum.
to such as to produce the KP-like spectrum.
In any case, KP-like spectra are only possible when there is a strong
magnetic field, with respect to
![]() .
Therefore, the existence of KP spectra indicates that synchrotron radiation is the most important energy
loss process in the region considered here. Furthermore, the variation of
.
Therefore, the existence of KP spectra indicates that synchrotron radiation is the most important energy
loss process in the region considered here. Furthermore, the variation of
![]() ,
if any, will cause a broadening of the spectral turn-over at low
frequencies.
,
if any, will cause a broadening of the spectral turn-over at low
frequencies.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H3106F18A.PS}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{H3106F18B.PS}
\end{figure}](/articles/aa/full/2003/22/aah3106/Timg137.gif) |
Figure 18:
Comparison of KP and JP spectra
under
|
We have investigated an alternative and very efficient method for the analysis of synchrotron spectra. We apply it both, to extended sources (like GRGs) and to the integrated flux densities of a sample of CSS sources. For all of them a thorough synchrotron ageing study has been performed which can be used for comparison. The information obtained from the spectral curvatures is manifold. The hot spots and jets possess pure power-law spectra, with particle ageing as expected. The spectral curvatures of the lobes exhibit both, spectral steepening and flattening.
In DA 240, there are CI spectra at the SW extremity, while KP/JP spectra show
up around the bright core of the SW lobe. We cannot find any bifurcation in
the diagram, which serves as the definite distinction between the KP model
and the JP model. More sensitive and/or higher-frequency observations are
needed to reveal the bifurcation between the KP and JP models as shown
between CI and KP/JP in DA 240. If a KP bifurcation is seen, it can be
interpreted as an identification of the existence of a strong
![]() ,
i.e.
,
i.e.
![]() .
As seen in Fig. 18, KP spectra can be identified. Otherwise, the
spectra would look like JP spectra, due to the influence of the isotropic
nature of
.
As seen in Fig. 18, KP spectra can be identified. Otherwise, the
spectra would look like JP spectra, due to the influence of the isotropic
nature of
![]() .
.
The high-frequency spectral indices start at values of around 0.5, which is
indicative of non-relativistic strong shock acceleration. A possible origin of
the shock could be the interaction of radio galaxies with their surrounding IGM/ICM (e.g. Enßlin et al. 2001). Adiabatic expansion, the other
significant energy loss process, does not affect the SCP-![]() diagram.
The results demonstrate that the SCP provides crucial parameters for the continuum
spectrum of synchrotron radiation, without the more complex modeling.
diagram.
The results demonstrate that the SCP provides crucial parameters for the continuum
spectrum of synchrotron radiation, without the more complex modeling.
Three characteristics that we have found in GRGs are not yet explained. The
first is the origin of the asymmetry of the injection spectra of the
radio lobes. Second, the physical explanation of the systematic flattening of
![]() compared to
compared to
![]() is unknown. Third, there is a
critical change of the re-acceleration efficiency showing up in the low- and
high-frequency regime. We will investigate the environments of GRGs to find
the possible reason.
is unknown. Third, there is a
critical change of the re-acceleration efficiency showing up in the low- and
high-frequency regime. We will investigate the environments of GRGs to find
the possible reason.
In conclusion, it can be stated that the SCP-![]() diagram proves to be an
efficient method to derive important properties of synchrotron spectra which
otherwise can be determined only with the much more complex synchrotron
ageing analysis. The SCP-
diagram proves to be an
efficient method to derive important properties of synchrotron spectra which
otherwise can be determined only with the much more complex synchrotron
ageing analysis. The SCP-![]() diagram and SCP map are especially useful
to analyze a large number of sources and a large number of spectral points
in a source. In those cases, the complex spectral analysis will give better
estimation. However, this alternative tool provides fast estimates without
losing accuracy significantly and provides an overview which is important
to understand synchrotron sources. Compared to the C-C diagram,
the SCP-
diagram and SCP map are especially useful
to analyze a large number of sources and a large number of spectral points
in a source. In those cases, the complex spectral analysis will give better
estimation. However, this alternative tool provides fast estimates without
losing accuracy significantly and provides an overview which is important
to understand synchrotron sources. Compared to the C-C diagram,
the SCP-![]() diagram extracts injection spectral indices and possible
synchrotron ageing models in a source more efficiently.
diagram extracts injection spectral indices and possible
synchrotron ageing models in a source more efficiently.
Acknowledgements
BWS is grateful to Heino Falke for discussions of the various shock acceleration conditions. KHM was supported by a Marie-Curie Fellowship. The authors are grateful to the anonymous referee for her/his fruitful comments.