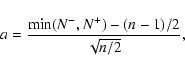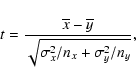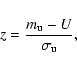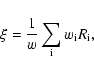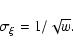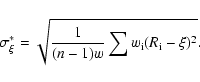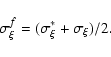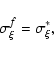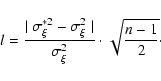A&A 403, 743-748 (2003)
DOI: 10.1051/0004-6361:20030398
The lost sunspot cycle: Reanalysis of sunspot statistics
I. G. Usoskin1 - K. Mursula2 -
G. A. Kovaltsov3
1 - Sodankylä Geophysical Observatory (Oulu unit), 90014
University of Oulu, Finland
2 -
Department of Physical Sciences, 90014 University of Oulu, Finland
3 -
Ioffe Physical-Techical Institute, 194021 St. Petersburg, Russia
Received 28 January 2003 / Accepted 11 March 2003
Abstract
We have recently suggested that one low sunspot cycle was
possibly lost
in 1790s (Usoskin et al. 2001, A&A, 370, L31).
In this paper we present the results of a rigorous statistical analysis
of all available sunspot observations around the suggested
additional cycle minimum in 1792-1793.
First we estimate the uncertainty of a monthly mean sunspot number
reconstructed
from a single daily observation.
Then we compare, using quantitative statistical tests, the average
level of sunspot
activity in 1792-1793 with the average activity during the minimum,
mid-declining and maximum phases of cycles in the well-measured
reference period 1850-1996.
We show that, contrary to the results by Krivova et al. (2002), the level of sunspot activity in 1792-1793 is statistically similar to that
in the minimum phase, and significantly different from that in the
mid-declining
and maximum phases.
Using the estimated uncertainties, we also calculate new, weighted
annual values of
 in
1790-1796 which show a clear minimum in 1792-1793 and a maximum in
1794-1795,
supporting the idea of an additional weak cycle in 1790's.
in
1790-1796 which show a clear minimum in 1792-1793 and a maximum in
1794-1795,
supporting the idea of an additional weak cycle in 1790's.
Key words: Sun: activity - Sun: sunspots - Sun: solar-terrestrial relations
We have recently suggested (Usoskin et al. 2001 - to be denoted here U01) that
one sunspot cycle was likely missed in 1790s.
Recently, a paper (Krivova et al. 2002 - to be denoted K02) has been
published where the authors criticize this idea claiming, e.g.,
that an additional sunspot minimum did not exist in 1792-1793.
Unfortunately, the statistical analysis performed in K02 is not
validated by quantitative tests and even contains several errors.
In this paper we reanalyze the arguments by K02 about the sunspot minimum
in 1792-1793.
We use quantitative statistical tests to show that the approach
suggested by K02 yields, when performed correctly, that the
available record of sunspot observations in 1790s does not exclude
but rather supports the possibility for an additional minimum in 1792-1793.
We also discuss the other, more indirect arguments presented in K02 against
the lost cycle.
In another recent paper (Usoskin et al. 2002a - to be denoted U02) we have
demonstrated that the idea of the lost cycle is supported by two independent
series of auroral observations, and that another solar activity proxy,
the cosmogenic radionuclides (14C and 10Be) do not
exclude the possible existence of the additional cycle.
We would like to note that we analyze here the group sunspot numbers
(GSN, denoted as  ;
see Fig. 1) provided by Hoyt & Schatten
(1998) and not the more traditional Wolf sunspot numbers (WSN), since
the GSN series contains the original (not interpolated) sunspot observations.
In the next section we study the question how a single daily
observation can represent
the monthly mean of sunspot activity.
Section 3 is devoted to a thorough quantitative analysis of sunspot
observations
and their statistics during the period under investigation.
In Sect. 4 we comment on some indirect arguments presented by K02 and
in Sect. 5 we give our main conclusions.
;
see Fig. 1) provided by Hoyt & Schatten
(1998) and not the more traditional Wolf sunspot numbers (WSN), since
the GSN series contains the original (not interpolated) sunspot observations.
In the next section we study the question how a single daily
observation can represent
the monthly mean of sunspot activity.
Section 3 is devoted to a thorough quantitative analysis of sunspot
observations
and their statistics during the period under investigation.
In Sect. 4 we comment on some indirect arguments presented by K02 and
in Sect. 5 we give our main conclusions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4271F1.eps}
\end{figure}](/articles/aa/full/2003/20/aah4271/Timg16.gif) |
Figure 1:
The monthly group sunspot numbers (Hoyt & Schatten 1998)
outside the years 1792-1793 are shown by the dashed curve.
Open dots with error bars depict the estimated monthly means
and their standard errors
in 1792-1793 (Table 1). The solid diamonds present
the estimated weighted annual averages in 1790-1796
(Table 2),
and the grey curve gives the spline fit to them.
Big grey dots denote the times of the two naked-eye sunspot observations
during the depicted interval (Yau & Stephenson 1988).
Vertical solid bars indicate the times of sunspot minima suggested
by U01, while the vertical dotted bar denotes the official minimum
of cycle 4 based on WSN series. |
The observations made in 1792-1793 according to known records (Hoyt & Schatten 1998)
are mainly isolated daily observations by single observers.
There are in total only 20 observations on 16 days during 1792-1793
(see, e.g., Table 2 in U01).
Moreover, the observations were not distributed uniformly over this time,
with 12 of them forming a period of 8 consecutive days in August-September 1793.
The other 8 observations, each on a different day,
are quite randomly spread over the period so that they all fall on
different months.
Moreover, there are no two consecutive months with sunspot observations,
except for August-September 1793.
The K02 paper claims that sunspot numbers in 1792-1793 are typical for
the mid-declining phase of a sunspot cycle and, therefore, exclude the
possibility of an additional minimum at this time.
They assumed implicitly that one isolated daily observation
 adequately
represents the corresponding monthly mean
adequately
represents the corresponding monthly mean
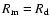 .
However, Hoyt & Schatten (1998) noted that at least 3 or 4 widely
separated days within a month are needed to form a more or less reliable
monthly mean.
Otherwise, they leave it up to the user of the GSN series to take
care of evaluating the usefulness of means of those months that
are less covered.
This advice was apparently not taken into account by K02 in their analysis.
.
However, Hoyt & Schatten (1998) noted that at least 3 or 4 widely
separated days within a month are needed to form a more or less reliable
monthly mean.
Otherwise, they leave it up to the user of the GSN series to take
care of evaluating the usefulness of means of those months that
are less covered.
This advice was apparently not taken into account by K02 in their analysis.
Here we examine the question of a correct way to form monthly means
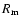 from isolated daily observations
from isolated daily observations
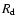 .
In order to do that, we analyzed all daily group sunspot numbers for the
period 1850-1996 when the data are reliable and contain no observational gaps.
We call this data set (more than 53 000 daily values) the reference population,
assuming that the statistical features of sunspot activity were the
same in 1792-1793 and during the reference period.
.
In order to do that, we analyzed all daily group sunspot numbers for the
period 1850-1996 when the data are reliable and contain no observational gaps.
We call this data set (more than 53 000 daily values) the reference population,
assuming that the statistical features of sunspot activity were the
same in 1792-1793 and during the reference period.
First, given one of the isolated daily sunspot values
 observed
in 1792-1793, we selected from the reference data set all the days
with a daily value close to
observed
in 1792-1793, we selected from the reference data set all the days
with a daily value close to
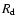 .
Then we collected the actual monthly means
.
Then we collected the actual monthly means
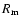 corresponding to
these selected days.
(If more than one appropriate daily value are found within a month, the
corresponding
corresponding to
these selected days.
(If more than one appropriate daily value are found within a month, the
corresponding
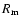 value
is counted as many times).
E.g., the highest daily observation
value
is counted as many times).
E.g., the highest daily observation
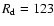 by Huber in May, 1793,
was compared with daily values from the interval [120-130] in the reference data set.
(The widths of the bins for the daily values
were chosen so as to
have sufficient statistics but still remaining within
by Huber in May, 1793,
was compared with daily values from the interval [120-130] in the reference data set.
(The widths of the bins for the daily values
were chosen so as to
have sufficient statistics but still remaining within 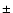 10% of
10% of
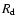 .)
The corresponding 1200 monthly values (for 450 months)
ranged from 52 to 213 with the mean being 115 (see Table 1).
If more than one daily observation was done in a month (as, e.g., in
August and September 1793)
we still can apply the above procedure by looking for the
corresponding set of
.)
The corresponding 1200 monthly values (for 450 months)
ranged from 52 to 213 with the mean being 115 (see Table 1).
If more than one daily observation was done in a month (as, e.g., in
August and September 1793)
we still can apply the above procedure by looking for the
corresponding set of
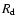 values
within the months of the reference period.
For the consecutive days of zero value in September 1793 we collected
the months
with at least five consecutive spotless days.
values
within the months of the reference period.
For the consecutive days of zero value in September 1793 we collected
the months
with at least five consecutive spotless days.
From the collected monthly values from the reference population
for each month in 1792-1793 with sunspot observations
we calculated the means
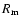 and their errors
and their errors
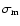 (see Table 1).
These are also shown in Fig. 1 as open dots with error bars.
Figure 2 shows samples of histograms of the collected
(see Table 1).
These are also shown in Fig. 1 as open dots with error bars.
Figure 2 shows samples of histograms of the collected
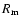 values.
The histogram distributions are apparently not Gaussian but
can be transformed to the Poisson form after scaling the X-axis.
Since a group sunspot number
values.
The histogram distributions are apparently not Gaussian but
can be transformed to the Poisson form after scaling the X-axis.
Since a group sunspot number
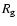 is the
number of sunspot groups G multiplied by a factor of 12.08 (Hoyt & Schatten 1998),
the real statistics behind GSN is the statistics of sunspot
groups (rather than sunspot numbers) which have much smaller values.
Therefore, if
is the
number of sunspot groups G multiplied by a factor of 12.08 (Hoyt & Schatten 1998),
the real statistics behind GSN is the statistics of sunspot
groups (rather than sunspot numbers) which have much smaller values.
Therefore, if
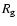 is reduced to G by dividing by a factor k = 12, the
statistics of
is reduced to G by dividing by a factor k = 12, the
statistics of
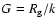 follow the Poisson distribution:
follow the Poisson distribution:
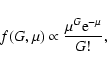 |
(1) |
where G is an integer 0, 1, 2, ... and 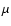 is the mathematical
expectation of the mean.
Values of
is the mathematical
expectation of the mean.
Values of 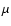 are given in the Col. 6 of Table 1
for all months containing sunspot observations during 1792-1793.
Figure 2 shows the best fit Poisson distributions
after rescaling of G back to
are given in the Col. 6 of Table 1
for all months containing sunspot observations during 1792-1793.
Figure 2 shows the best fit Poisson distributions
after rescaling of G back to
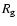 .
Thus, one can reconstruct a reliable monthly mean
.
Thus, one can reconstruct a reliable monthly mean
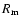 (see
Table 1) even from a single daily observation
(see
Table 1) even from a single daily observation
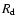 but its uncertainty is an important factor and should be
taken into account.
but its uncertainty is an important factor and should be
taken into account.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4271F2.eps}
\end{figure}](/articles/aa/full/2003/20/aah4271/Timg22.gif) |
Figure 2:
Samples of histogram distributions of monthly
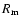 together with
the rescaled best-fit Poisson distribution functions.
The four panels depict the cases of
at least five consecutive zero daily
together with
the rescaled best-fit Poisson distribution functions.
The four panels depict the cases of
at least five consecutive zero daily
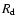 values within one
month (marked as 5*0),
and at least one
values within one
month (marked as 5*0),
and at least one
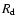 within the interval [20-25], [45-50] or
[90-100], respectively.
within the interval [20-25], [45-50] or
[90-100], respectively. |
It was an interesting idea by K02 to calculate the average sunspot
level for 1792-1793 (denoted as
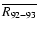 ), i.e.,
the time around the
suggested minimum, and to compare it to the level of some later,
better covered solar cycles.
However, it is not correct to calculate
), i.e.,
the time around the
suggested minimum, and to compare it to the level of some later,
better covered solar cycles.
However, it is not correct to calculate
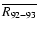 as a
simple arithmetic average of monthly means
as a
simple arithmetic average of monthly means
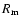 (as done by K02) since
they are of greatly unequal accuracy, as discussed in Sect. 2.
(Calculating the
(as done by K02) since
they are of greatly unequal accuracy, as discussed in Sect. 2.
(Calculating the
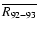 mean from daily values is not
correct either because daily values are not independent in Aug.-Sep. 1793,
as required by the standard averaging methods).
In such a case the
mean from daily values is not
correct either because daily values are not independent in Aug.-Sep. 1793,
as required by the standard averaging methods).
In such a case the
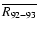 mean must be calculated
as a weighted average.
Details of this standard averaging method are given in Appendix.
The weights
mean must be calculated
as a weighted average.
Details of this standard averaging method are given in Appendix.
The weights
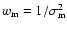 used for the averaging are also given in
Table 1.
Our final estimate of
used for the averaging are also given in
Table 1.
Our final estimate of
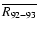 is
is
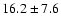 ,
which is less than half of the value 41 given by K02 (no error
estimated there).
We note that
,
which is less than half of the value 41 given by K02 (no error
estimated there).
We note that
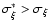 (see Appendix) in this
case and the factor l (Eq. (A.6)) is about 7,
implying that the sample series is inhomogeneous and contains a
large systematic error.
If the suspicious observation by Huber (
(see Appendix) in this
case and the factor l (Eq. (A.6)) is about 7,
implying that the sample series is inhomogeneous and contains a
large systematic error.
If the suspicious observation by Huber (
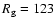 )
is discarded as
suggested by K02 then
)
is discarded as
suggested by K02 then
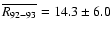 ,
cf.
the value 31 given by K02.
Accordingly, K02 heavily overestimated the average sunspot level in 1792-1793
by using a simple arithmetic average of the monthly values, i.e. taking them
with equal weights.
,
cf.
the value 31 given by K02.
Accordingly, K02 heavily overestimated the average sunspot level in 1792-1793
by using a simple arithmetic average of the monthly values, i.e. taking them
with equal weights.
Using the monthly means and their errors, we also calculated the weighted
annual
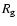 values and their errors for the years 1790-1796 (see
Table 2).
Note that if there are more than 4 independent (i.e., sufficiently
widely distributed) observation days within a month, the mean and
the standard error of
values and their errors for the years 1790-1796 (see
Table 2).
Note that if there are more than 4 independent (i.e., sufficiently
widely distributed) observation days within a month, the mean and
the standard error of
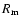 can be calculated directly from
the available daily values
can be calculated directly from
the available daily values
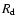 without employing histograms
similar to Fig. 2.
The time profile of the annual
without employing histograms
similar to Fig. 2.
The time profile of the annual
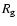 values depicted by diamonds in
Fig. 1
clearly suggests for an additional minimum at the turn of 1792-1793
and a maximum in 1794-1795.
values depicted by diamonds in
Fig. 1
clearly suggests for an additional minimum at the turn of 1792-1793
and a maximum in 1794-1795.
Table 2:
The formal (Hoyt & Schatten 1998) and weighted annual averages of
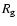 and their errors in 1790's.
and their errors in 1790's.
| year |
formal |
weighted |
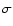 |
| 1790 |
61.5 |
57 |
12.5 |
| 1791 |
43.2 |
39.5 |
5.3 |
| 1792 |
42 |
19.2 |
7.3 |
| 1793 |
41 |
12.4 |
5.3 |
| 1794 |
30.2 |
23.4 |
5.2 |
| 1795 |
15.7 |
18.8 |
3 |
| 1796 |
13.7 |
12.9 |
3.8 |
Following K02, we now estimate in which phase of the solar cycle the
sunspot activity level
is statistically similar to
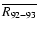 .
We have plotted the obtained
.
We have plotted the obtained
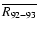 together with the
running 2-year mean of sunspots (grey curve) for the reference
period 1850-1996 in Fig. 3a.
In the same figure, we have also included the running 2-year sunspot
activity level
obtained by the filtering method of K02, i.e., by selecting for each 730-day
interval only those 16 daily
together with the
running 2-year mean of sunspots (grey curve) for the reference
period 1850-1996 in Fig. 3a.
In the same figure, we have also included the running 2-year sunspot
activity level
obtained by the filtering method of K02, i.e., by selecting for each 730-day
interval only those 16 daily
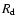 values that are separated in time
in the same way as the observations in 1792-1793.
This filter gives the value
values that are separated in time
in the same way as the observations in 1792-1793.
This filter gives the value
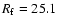 for 1792-1793 (see
Fig. 3).
(Note that the horizontal lines in Fig. 3 of K02 present
the unweighted averages in 1792-93, not the filter values, contrary
to figure caption.)
Figure 3a shows that the obtained value of
for 1792-1793 (see
Fig. 3).
(Note that the horizontal lines in Fig. 3 of K02 present
the unweighted averages in 1792-93, not the filter values, contrary
to figure caption.)
Figure 3a shows that the obtained value of
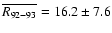 corresponds very well
to the values of
corresponds very well
to the values of
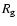 around solar minima rather than to the
mid-declining phase, contrary to K02.
We will test this quantitatively in Sect. 3.3.
around solar minima rather than to the
mid-declining phase, contrary to K02.
We will test this quantitatively in Sect. 3.3.
The most systematic part of sunspot observations in 1792-1793
was from August 30 until September 4, 1793.
No sunspots were observed during this period.
Moreover, there were three independent observers on one day, all reporting
no sunspots (Hoyt & Schatten 1998).
K02 correctly listed some examples when several consecutive
spotless days can be found even in the middle of declining phase of a cycle.
However, noting that this the only period of consecutive observations in
1793, we must calculate how probable it is to find a 6-day spotless period,
taking the period randomly within a year.
Using the reference population, we have calculated this probability P(6*0).
Starting from the first day of each year, we slided the 6-day window
through one year of data with 1-day time step, counting the number N of times when this
window finds only zeroes.
(The last window includes 5 days of the next year).
Then the probability is defined as
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4271F3.eps}
\end{figure}](/articles/aa/full/2003/20/aah4271/Timg33.gif) |
Figure 3:
Top panel: filtered (thin noisy curve) and the 2-year
smoothed (grey curve) group
sunspot numbers.
The thick solid horizontal line and hatched area around it
correspond to the weighted sunspot average in
1792-1793
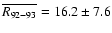 .
The dotted horizontal line denotes the filtered sunspot value .
The dotted horizontal line denotes the filtered sunspot value
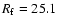 in 1792-1793.
Bottom panel: probability to find a spotless 6-day period within
one year (grey curve P(6*0));
combined probability to find both a spotless 6-day period and a
day with
in 1792-1793.
Bottom panel: probability to find a spotless 6-day period within
one year (grey curve P(6*0));
combined probability to find both a spotless 6-day period and a
day with
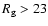 or
or
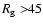 within one year (dotted
within one year (dotted
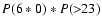 or solid
or solid
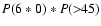 lines, respectively).
lines, respectively). |
The time series of P(6*0) is shown in the lower panel of Fig. 3.
One can see that the probability peaks within a few years around cycle minima
and is zero in all other years.
Note also the low probability to find a spotless 6-day period during
the recent high activity cycles, even around minima.
In addition to this spotless period, daily sunspot values of
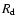 =
15, 24, 48 and 123 were reported in 1793.
We have also calculated the combined probability
P(6*0)*P(>R) to
find a spotless period and at
least one day with
=
15, 24, 48 and 123 were reported in 1793.
We have also calculated the combined probability
P(6*0)*P(>R) to
find a spotless period and at
least one day with
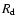 above a given value R at any time of the year.
The probabilities for R=23 and R=45 are also given in the lower
panel of Fig. 3.
The probability is still quite high for
above a given value R at any time of the year.
The probabilities for R=23 and R=45 are also given in the lower
panel of Fig. 3.
The probability is still quite high for
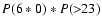 ,
but
decreases greatly for
,
but
decreases greatly for
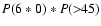 .
However, the combined probability to find a spotless 6-day period
and at least one daily observation with
.
However, the combined probability to find a spotless 6-day period
and at least one daily observation with
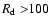 gets non-zero
values only in few years,
with the maximum probability
gets non-zero
values only in few years,
with the maximum probability
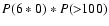 of about 0.0033 in 1955.
Therefore, it is highly improbable to find both a spotless 6-day
period and a day with
of about 0.0033 in 1955.
Therefore, it is highly improbable to find both a spotless 6-day
period and a day with
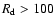 when they are taken randomly within one year.
This inconsistency gives further motivation for the concern about the
correctness of the
very high sunspot value
when they are taken randomly within one year.
This inconsistency gives further motivation for the concern about the
correctness of the
very high sunspot value
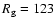 observed by Huber in May 1793.
Let us remind (see U01) that the high
observed by Huber in May 1793.
Let us remind (see U01) that the high
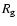 corresponding to this
observation is due to the very large
individual correction factor of Huber (2.564) which is within the 5 largest
factors among the 463 observers whose data were included in the GSN
series (Hoyt & Schatten 1998).
Therefore, the four sunspot groups reported by Huber on 28 May, 1793,
would yield
corresponding to this
observation is due to the very large
individual correction factor of Huber (2.564) which is within the 5 largest
factors among the 463 observers whose data were included in the GSN
series (Hoyt & Schatten 1998).
Therefore, the four sunspot groups reported by Huber on 28 May, 1793,
would yield
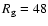 but the large correction factor leads to the
much higher GSN value.
Note also that Hoyt & Schatten (1998) regard observers with individual
correction factors above 2
as poor observers whose observations should be discarded if possible.
but the large correction factor leads to the
much higher GSN value.
Note also that Hoyt & Schatten (1998) regard observers with individual
correction factors above 2
as poor observers whose observations should be discarded if possible.
We now make quantitative tests of the null hypothesis that a small
sample population (sunspot observations during 1792-1793) is
statistically similar to a given reference population.
These tests can be found in most handbooks and textbooks on statistical
analysis (see e.g.,
Hudson 1964; Agekyan 1972; Sachs 1972).
The size of the sample population is too small to analyze the shape
of the distribution function, but we can test the hypothesis of the
equality of means of the two populations.
We considered three reference populations from the reference period
of 1850-1996:
the minimum, maximum and mid-declining phase populations
including all the daily
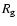 values in 2-year intervals around
sunspot minima, maxima and in the middle of the declining phase, respectively.
We applied three different statistical tests for both the daily observations
(16 daily measurements in the 1792-1793 sample and about 10 000 points
in each of the reference populations) and for the monthly averages
(9 and about 320 points, respectively).
The means and standard deviations
of the reference populations are given in Table 3.
values in 2-year intervals around
sunspot minima, maxima and in the middle of the declining phase, respectively.
We applied three different statistical tests for both the daily observations
(16 daily measurements in the 1792-1793 sample and about 10 000 points
in each of the reference populations) and for the monthly averages
(9 and about 320 points, respectively).
The means and standard deviations
of the reference populations are given in Table 3.
First, we applied the Single-Sample Sign test to the null hypothesis.
To each point of the sample population
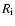 ,
a sign "-" or "+" is
assigned depending on whether
,
a sign "-" or "+" is
assigned depending on whether
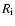 is smaller or greater than the mean value of the reference
population, respectively.
Then the number of "+'' elements N+ and "-'' elements N- is
counted and the value of a is calculated:
is smaller or greater than the mean value of the reference
population, respectively.
Then the number of "+'' elements N+ and "-'' elements N- is
counted and the value of a is calculated:
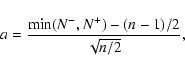 |
(3) |
where n is the size of the sample population.
If the sample population has the same mean as the reference population,
the mathematical expectation of a is zero.
From the value of a the probability
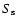 of a false rejection of
the null hypothesis is calculated.
If a is significantly different (at the level of
of a false rejection of
the null hypothesis is calculated.
If a is significantly different (at the level of
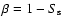 )
from zero then the null hypothesis of
the equality of the two means should be rejected at the significance
level
)
from zero then the null hypothesis of
the equality of the two means should be rejected at the significance
level 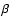 .
Note that the value of
.
Note that the value of
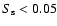 indicates that the two populations
have significantly different means (at the significance level of 0.95).
This test gives a reliable estimate only if the sample size is
significantly larger than 10 elements.
Only the daily data set fulfills this requirement, and the calculated
values of
indicates that the two populations
have significantly different means (at the significance level of 0.95).
This test gives a reliable estimate only if the sample size is
significantly larger than 10 elements.
Only the daily data set fulfills this requirement, and the calculated
values of
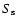 and a are given in Table 3.
and a are given in Table 3.
Next we applied the so-called t-test which computes t value of Student's statistics:
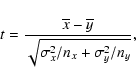 |
(4) |
where
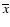 ,
,
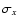 ,
nx and
,
nx and
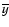 ,
,
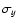 ,
ny are the mean,
standard deviation and the size of the sample and reference
populations, respectively.
We adopted here
,
ny are the mean,
standard deviation and the size of the sample and reference
populations, respectively.
We adopted here
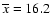 ,
,
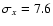 and nx=9 for the monthly
data and
and nx=9 for the monthly
data and
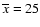 ,
,
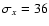 and
nx=16 for the daily data
in 1792-1793.
The values of
and
nx=16 for the daily data
in 1792-1793.
The values of
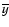 and
and
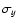 for the reference populations
are given in Table 3.
From the t-statistics, one can compute the significance level
for the reference populations
are given in Table 3.
From the t-statistics, one can compute the significance level
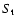 to accept the null hypothesis (or reject it at the level of
to accept the null hypothesis (or reject it at the level of
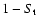 ),
with the values of
),
with the values of
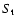 given in Table 3.
given in Table 3.
As a third test we applied the non-parametric
Wilcoxon Rank Sum test which tests the null hypothesis of the relative
unbiasedness of the two populations.
There the z-statistics is computed
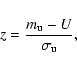 |
(5) |
where U is the rank sum of the sample population x, and
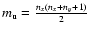 and
and
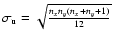 are the
mathematical expectations of the mean and standard deviation of U.
Then, the value of the probability
are the
mathematical expectations of the mean and standard deviation of U.
Then, the value of the probability
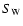 to accept the null
hypothesis is calculated from z.
The results of this test (see Table 3) imply that the
sample population is likely unbiased with respect to the minimum-like
reference population but it is significantly biased with respect to
both the mid-declining and maximum-like reference populations.
to accept the null
hypothesis is calculated from z.
The results of this test (see Table 3) imply that the
sample population is likely unbiased with respect to the minimum-like
reference population but it is significantly biased with respect to
both the mid-declining and maximum-like reference populations.
The results of all the above tests are consistent with each other and suggest
that only the minimum-like reference population may have the same mean as
the 1792-1793 sample, while the hypothesis of the equality of the means
should be rejected for both
the maximum and the declining phase reference populations at a high
significance level.
This result is robust and reliable, being confirmed by three different and
independent statistical tests and for two different time resolutions
(daily vs. monthly).
Note that the first and third tests do not require any statistical estimates
(e.g., mean, error) of the sample population, and are therefore
independent of our analysis of this population presented above.
(Moreover, the third test is even independent of the statistical estimates
of the reference populations).
This implies, contrary to K02, that the sample population of
1792-1793 is statistically
similar to the minimum-like reference
populations and significantly different from both the maximum and
declining phase populations.
Here we comment on some indirect arguments raised by K02 against the
possibility of the new cycle.
Length of the lost cycle.
K02 misinterpreted the dates of cycle extremes suggested in U01.
E.g., when defining the length of the lost cycle (see Table 1 of
K02), they adopted from U01 only the date of the minimum between
cycles 3 and 4
and 4 (called 4* and 4a in K02).
As the date of the next minimum (between cycles 4' (4a) and 5) they
used the "official'' minimum in 1798.3, leading to a very short length for the lost cycle.
However, this official minimum (dotted vertical bar in Fig. 1)
was calculated using the Wolf sunspot series, which is different
from the group sunspot series analyzed here, in U01 and in K02.
Applying the standard 13-month running mean (see, e.g., Gleissberg 1944; Harvey & White 1999)
to the GSN series we found the minimum to be in December 1799 as given in Table 3 in U01.
(The 13-month running mean gives the value of 5.4 in 1798.3 and 3.6 in 1799.9).
This implies that the length of the lost cycle 4
(called 4* and 4a in K02).
As the date of the next minimum (between cycles 4' (4a) and 5) they
used the "official'' minimum in 1798.3, leading to a very short length for the lost cycle.
However, this official minimum (dotted vertical bar in Fig. 1)
was calculated using the Wolf sunspot series, which is different
from the group sunspot series analyzed here, in U01 and in K02.
Applying the standard 13-month running mean (see, e.g., Gleissberg 1944; Harvey & White 1999)
to the GSN series we found the minimum to be in December 1799 as given in Table 3 in U01.
(The 13-month running mean gives the value of 5.4 in 1798.3 and 3.6 in 1799.9).
This implies that the length of the lost cycle 4 is about 7 years
(as suggested in U01, U02), and not 5 years as in Table 1 of K02.
This modifies the whole analysis of cycle lengths as shown in Figs. 7
and 8 in K02.
An appropriate analysis of cycle lengths is given in U02, together
with the analysis of the relation between the cycle amplitude and the length of the
ascending and descending phases of a cycle (the so-called Waldmeier
relations; Waldmeier 1960).
The results presented in U02 imply that the introduction of the new
cycle does not
change significantly the cycle length distribution or the
length-vs-amplitude statistics.
is about 7 years
(as suggested in U01, U02), and not 5 years as in Table 1 of K02.
This modifies the whole analysis of cycle lengths as shown in Figs. 7
and 8 in K02.
An appropriate analysis of cycle lengths is given in U02, together
with the analysis of the relation between the cycle amplitude and the length of the
ascending and descending phases of a cycle (the so-called Waldmeier
relations; Waldmeier 1960).
The results presented in U02 imply that the introduction of the new
cycle does not
change significantly the cycle length distribution or the
length-vs-amplitude statistics.
Naked-eye observations.
As another argument that this time (i.e., 1792-1793) did not
correspond to sunspot minimum", K02 used the fact that a naked-eye sunspot observation was reported
in 1792 (Yau & Stephenson 1988; see also Fig. 1).
However, there is another naked-eye observation in Feb. 1799
(Yau & Stephenson 1988) which was not included in Fig. 1 of K02.
This observation falls between the official and the suggested minimum of
cycle 5, in a period which was well covered by sunspot observations
and when sunspot activity was even lower than the average level in 1792
(see Fig. 1).
Note also that eleven naked-eye sunspot observations are listed in
the same catalogue during the
Maunder minimum when sunspots were extremely sparse.
This implies that, contrary to the suggestion of K02, a naked-eye
sunspot observation in 1792
does not exclude the possibility of an additional sunspot minimum in 1792-1793.
Moreover, as argued by Eddy (1976, 1983), naked-eye observations
alone are not a reliable
indicator of sunspot activity.
Skewness.
Figure 9 and the end of Sect. 5 of K02 discuss skewness which is supposed to be
a quantitative measure of a cycle profile".
This is apparently a lapse since K02 calculated the skewness of the
distribution function of
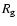 values, not of the cycle shape.
(Note also that the equation defining skewness in K02 has a typo,
missing the power 3).
Also, we would like to note that calculating the skewness of sunspot
number distribution for
the new cycle using only available observations leads to an overestimate
because sunspot numbers from the minimum and
ascending phases are under-represented in the distribution.
If one uses the sunspot activity profile suggested in U01
to fill the gaps in the beginning of the new cycle
(see also Fig. 1), the corresponding skewness will be 0.76, i.e.,
far below the value of 2.7 given in K02.
Accordingly, the value of the skewness of the new cycle is well
within the range
of other cycles and does not form an exceptional outlier as suggested in K02.
values, not of the cycle shape.
(Note also that the equation defining skewness in K02 has a typo,
missing the power 3).
Also, we would like to note that calculating the skewness of sunspot
number distribution for
the new cycle using only available observations leads to an overestimate
because sunspot numbers from the minimum and
ascending phases are under-represented in the distribution.
If one uses the sunspot activity profile suggested in U01
to fill the gaps in the beginning of the new cycle
(see also Fig. 1), the corresponding skewness will be 0.76, i.e.,
far below the value of 2.7 given in K02.
Accordingly, the value of the skewness of the new cycle is well
within the range
of other cycles and does not form an exceptional outlier as suggested in K02.
Cosmogenic radionuclides.
On the basis of a visual analysis of the cosmogenic 10Be and 14C time series, K02 made
the correct conclusion that they do not provide evidence for an
extra cycle in 1790s.
However, in U02 we have analysed by numerical modeling
(using models by Solanki et al. 2000 and Usoskin et al. 2002b) the response of 10Be isotope
concentration to the standard sunspot activity in 1790s and the
new sunspot activity profile including the new cycle.
The results clearly demonstrate that the differences between
the two 10Be response profiles
are significantly below observational errors.
Therefore, the 10Be data are not able to distinguish between the
two alternatives.
Moreover, the radiocarbon 14C isotope is even less sensitive
than 10Be to the fast and rather small changes of solar activity in 1790s
implied by the new cycle.
Therefore, as argued in U02, the cosmogenic radionuclide data can
neither prove nor disprove the existence of the suggested new cycle in 1790s.
Aurorae.
An analysis of auroral observations in 1790's reveals a small but distinct
peak of auroral activity in 1796-1797 (e.g., K02, U02), i.e., a couple of years
after the suggested additional maximum.
Although the existence of this peak which appears in the three independent data
series analyzed in K02 and U02 is beyond doubt, its origin can be questioned.
In U02 this peak was interpreted as the main peak of auroral activity in cycle 4 (4a).
This would be in accordance with the common situation where auroral maxima often occur
a couple of years after the sunspot cycle maximum.
On the other hand, K02 regarded it to be due to the recurrent activity caused by
high speed streams occurring very late in cycle 3
(4a).
This would be in accordance with the common situation where auroral maxima often occur
a couple of years after the sunspot cycle maximum.
On the other hand, K02 regarded it to be due to the recurrent activity caused by
high speed streams occurring very late in cycle 3 (4*).
We note that the recurrent streams usually occur earlier in the cycle and definitely
lead to a much higher peak, which is often higher or of the same order
of magnitude as the main peak.
Rather, the peak in 1796-1797 was only about 10% of the main auroral activity peak of
cycle 3
(4*).
We note that the recurrent streams usually occur earlier in the cycle and definitely
lead to a much higher peak, which is often higher or of the same order
of magnitude as the main peak.
Rather, the peak in 1796-1797 was only about 10% of the main auroral activity peak of
cycle 3 (4*) and occurred just prior to the official minimum of cycle 4.
Therefore, the existence of the new cycle is not contradicted but slightly favored
by the auroral data.
(4*) and occurred just prior to the official minimum of cycle 4.
Therefore, the existence of the new cycle is not contradicted but slightly favored
by the auroral data.
We have performed a careful statistical analysis of the sunspot
observations in 1790s in order to further study the possibility of a
lost cycle at this time (Usoskin et al. 2001).
Using three independent statistical tests, we have shown that the
average level of sunspot activity in 1792-1793 is similar to that
around sunspot cycle minima during the more recent, well observed
years (1850-1996),
but is significantly
different from the activity either in the mid-declining phase or
around sunspot maxima.
This is contrary to the results presented by Krivova et al. (2002)
who, when calculating monthly and yearly sunspot number averages,
did not take into account the extreme sparseness of sunspot
observations and the implied inaccuracy of the calculated monthly and
yearly means.
Our results show that the existence of a new cycle in 1790s does not
contradict with any available sunspot observations or indirect solar proxies
(see also U01, U02).
Moreover, our refined analysis of sunspot activity in 1790s
gives additional evidence for a sunspot minimum in 1792-93,
supporting the existence of a new cycle in 1790's.
Acknowledgements
The financial support by the Academy of Finland
is gratefully acknowledged. GAK was partly supported by the program
Non-stationary Processes in Astronomy" of Russian Academy
of Sciences.
The method of weighted average is a standard approach to analyze a
series of measurements
with unequal accuracy.
Let us assume that the individual data points
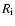 are independent
measurements of the same quantity
are independent
measurements of the same quantity
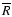 (e.g., the average sunspot number in 1792-1793)
but with individual errors
(e.g., the average sunspot number in 1792-1793)
but with individual errors
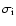 .
The individual weights
.
The individual weights
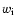 are
inversely proportional to the squared
errors
are
inversely proportional to the squared
errors
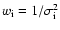 .
The weighted average is then calculated as
.
The weighted average is then calculated as
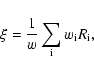 |
(A.1) |
where
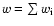 .
The expected mean error of
.
The expected mean error of 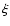 is
is
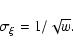 |
(A.2) |
On the other hand, the actual mean error of 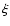 can be calculated from
can be calculated from
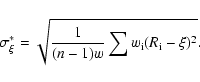 |
(A.3) |
In an ideal case, the values of
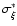 and
and
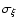 should be equal
but generally they are not since the individual measurements always
contain random errors
and may also contain systematic errors.
If
should be equal
but generally they are not since the individual measurements always
contain random errors
and may also contain systematic errors.
If
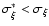 ,
the origin of the difference
between them is random, and their
arithmetic average can be taken as the final estimate of the mean
error of
,
the origin of the difference
between them is random, and their
arithmetic average can be taken as the final estimate of the mean
error of 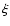 :
:
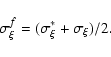 |
(A.4) |
If, however,
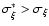 ,
then
,
then
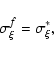 |
(A.5) |
and a factor l should be calculated:
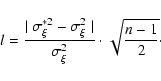 |
(A.6) |
If l<2 then the difference between
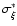 and
and
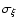 is most likely
of random origin (at the significance level of 0.95),
otherwise a systematic error exists in the measurement series.
is most likely
of random origin (at the significance level of 0.95),
otherwise a systematic error exists in the measurement series.
Finally one can say that the real value of
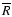 lies within
the interval of
lies within
the interval of
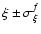 with the confidence level of 0.68.
with the confidence level of 0.68.
-
Agekyan, T. A. 1972, The Basics of Errors Theory for Astronomers
and Physicists
(Moscow: Nauka, in Russian)
-
Eddy, J. A. 1976, Science, 192, 1189
NASA ADS
-
Eddy, J. A. 1983, Sol. Phys., 89, 195
NASA ADS
-
Gleissberg, W. A. 1944, Terr. Magn. Atm. Electr., 49, 243
-
Harvey, K. L., & White, O. R. 1999, J. Geophys. Res., 104, 19 759
-
Hoyt D. V., & K. Schatten 1998, Sol. Phys., 179, 189
NASA ADS
-
Hudson, D. 1964, Statistics: Lectures on Elementary Statistics
and Probability (Geneva)
-
Krivova, N. A., Solanki, S. K., & Beer, J. 2002, A&A, 396, 235
NASA ADS
-
Sachs, L. 1972, Statistische Auswaertungsmethoden
(Berlin: Springer-Verlag)
-
Solanki, S. K., Schüssler, M., & Fligge, M. 2000, Nature, 408, 445
NASA ADS
-
Usoskin, I. G., Mursula, K., & Kovaltsov, G. A. 2001, A&A, 370, L31
NASA ADS
-
Usoskin, I. G., Mursula, K., & Kovaltsov, G. A. 2002a, Geophys. Res.
Lett., 29, 36
-
Usoskin, I. G., Mursula, K., Solanki, S., Schüssler, M., & Kovaltsov,
G. A. 2002b, J. Geophys. Res., 107, 13
-
Waldmeier, M. 1960, The Sunspot Activity in the Years 1610-1960
(Zurich: Zurich Schulthess & Company AG)
-
Yua, K. K., & Stephenson, F. R. 1988, Quat. J. R. Astron. Soc.,
29, 175
NASA ADS
Copyright ESO 2003
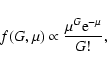
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4271F2.eps}
\end{figure}](/articles/aa/full/2003/20/aah4271/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4271F3.eps}
\end{figure}](/articles/aa/full/2003/20/aah4271/Timg33.gif)