A&A 403, 261-275 (2003)
DOI: 10.1051/0004-6361:20030357
Monte Carlo transition probabilities. II.
L. B. Lucy
Astrophysics Group, Blackett Laboratory, Imperial College
London, Prince Consort Road, London SW7 2AZ, UK
Received 31 January 2003 / Accepted 6 March 2003
Abstract
The macroscopic quantizations of matter into macro-atoms and radiant and
thermal energies into r- and k-energy packets initiated in Paper I is
completed
with the definition of transition probabilities governing energy
flows to and from the thermal pool. The resulting Monte Carlo method is then
applied to the problem of computing the hydrogen spectrum of a type II
supernova. This test problem is used to demonstrate the scheme's consistency
as the number of energy
packets
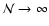 ,
to investigate the accuracy of
Monte Carlo estimators for radiative rates, and to illustrate the convergence
characteristics of the geometry-independent, constrained
,
to investigate the accuracy of
Monte Carlo estimators for radiative rates, and to illustrate the convergence
characteristics of the geometry-independent, constrained 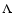 -iteration
method employed to
obtain the NLTE stratifications of temperature and level populations. In
addition, the
method's potential, when combined with analytic ionization and excitation
formulae, for obtaining useful approximate NLTE solutions is
emphasized.
-iteration
method employed to
obtain the NLTE stratifications of temperature and level populations. In
addition, the
method's potential, when combined with analytic ionization and excitation
formulae, for obtaining useful approximate NLTE solutions is
emphasized.
Key words: methods: numerical - radiative transfer - stars: atmospheres
- stars: supernovae: general - line: formation
In an earlier paper (Lucy 2002; Paper I), a technique for imposing the
constraint of
statistical equilibrium on Monte Carlo (MC)
transfer codes was developed. This was achieved by first replacing
the rate-equation representation of statistical equilibrium by
one involving macroscopic energy flows and then quantizing these flows into
indivisible
energy packets. These e-packets - the MC quanta -
contain either radiant
energy (r-packets) or kinetic energy (k-packets) and undergo changes on
interaction with matter in
accordance with certain probabilistic rules. Because these rules are
analogous to
the transition probabilities that govern a real atom's interactions with
photons and electrons (or other colliding species), they can be
interpreted as (MC) transition probabilities that govern a
macro-atom's interactions with r- and k-packets,
with the macro-atom simply
representing the atoms of a particular species in a finite volume element.
In addition to providing its theoretical basis,
Paper I subjected the macro-atom formalism to various numerical tests,
each of which concerned a single point in a stratified atmosphere. In the
first group of tests, the consistency of the scheme was confirmed by
demonstrating that, when used with the exact level
populations, the technique asymptotically reproduces the correct line- and
continuum emissivities. But consistency, though necessary, does not guarantee
that an effective NLTE code can be developed with this technique.
Accordingly, Paper I also tested the sensitivity of the MC emissivities to departures from the exact level populations, since
extreme sensitivity would make it unlikely that the scheme would be
successful in an iterative search for a NLTE solution. Fortunately,
the emissivities were found to be remarkably insensitive to the level
populations, thus suggesting good convergence characteristics.
Given these successes with one-point tests, the next step is
evidently to apply the macro-atom formalism to a stratified medium.
Possible test problems are many and varied since
the technique is quite general: potentially, it applies to
multi-species
plasmas, to multi-dimensional geometries, and to problems with
non-radiative heating. But given the technique's novelty, step-by-step
testing is advisable, starting with the simplest of problems.
Accordingly, this paper treats a 1D medium comprising just one
atomic species and subject only to radiative heating.
Specifically,
the problem is to compute the level populations and kinetic temperature
throughout the outer envelope of a type II supernova, which we take to
be pure hydrogen. In such extended, low density envelopes, substantial
departures from LTE arise due to the strong dilution of continuum
radiation and to the negligible importance of collisional excitations.
The technique's ability to
solve non-trivial NLTE problems is therefore tested. In particular, the
convergence behaviour of
the iterations required to obtain the level populations and the
temperature stratification can be investigated. Moreover, this test serves to
illustrate the structure of NLTE codes using the macro-atom formalism.
In this section, the basic assumptions concerning the structure of the
supernova and the relevant atomic physics are stated. In contrast to previous MC codes for SNe (Lucy 1987; Mazzali & Lucy 1993; Lucy 1999b;
Mazzali 2000), the interest
here is to test technique rather than to construct a code immediately
suitable for
analysing observational data. Accordingly, state-of-the-art modelling
precision with respect to the SN envelope or to the atomic physics and
radiative transfer is of no concern.
In formulating this test problem, we take the computational domain D to be
exterior to the layers where the energy released by radioactive decays is
thermalized. Then, with the further
assumptions that the radiative cooling and recombination time scales are
small compared to the expansion time scale, the principles governing spectrum
formation are statistical and thermal equilibrium in every local co-moving
frame within D.
Because the energy sources are interior to the lower
boundary (r = R) of D, this calculation does not predict the SN's
luminosity L, which is therefore a parameter. For the same
reason, a boundary condition at r = R on
the outwardly-directed radiation field is required. This is taken to be
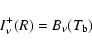 |
(1) |
where 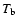 ,
the black-body temperature, remains to be determined.
,
the black-body temperature, remains to be determined.
In Eq. (1) and throughout this paper,  denotes frequency
in the matter frame; frequency in the rest frame will be denoted by
denotes frequency
in the matter frame; frequency in the rest frame will be denoted by 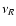 .
Similarly, the energy of an r-packet in the matter and rest
frames will be denoted by
.
Similarly, the energy of an r-packet in the matter and rest
frames will be denoted by
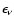 and
and
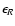 ,
respectively.
,
respectively.
The density distribution at time t after the explosion is obtained
as usual from the assumption of homologous expansion. Thus
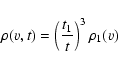 |
(2) |
where v = r/t is the constant velocity of the mass layer that is at radius r1 at time t1, and
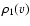 is the density-velocity profile at
elapsed
time t1. The profile adopted is that of Arnett's (1988) explosion
model for SN1987A.
is the density-velocity profile at
elapsed
time t1. The profile adopted is that of Arnett's (1988) explosion
model for SN1987A.
With the further assumption of a pure H composition,
the atomic number density is
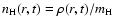 .
.
For the problem thus defined, the basic parameters
are t and L. The test calculation of Sect. 7 is
carried out at t = 9.8 days, and L(t) is required to be
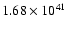 erg s-1, the value determined observationally
for SN 1987A (Suntzeff & Bouchet 1990).
erg s-1, the value determined observationally
for SN 1987A (Suntzeff & Bouchet 1990).
In addition to setting parameters, the location of the lower boundary
must be specified. This is taken to be the layer moving at
v1 = 6500 km s-1, corresponding to
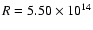 cm.
cm.
The MC calculation is performed for a discretized version of the
SN's envelope. Specifically, the envelope is modelled as 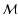 constant-density spherical shells, within each of which the temperature T and the level populations ni are also constant.
constant-density spherical shells, within each of which the temperature T and the level populations ni are also constant.
The independent variable is x = R/r, in terms of which
the shells have constant thickness
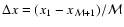 ,
with x1 = 1 and
,
with x1 = 1 and
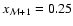 .
The mean radius of the mth shell is
defined to be
.
The mean radius of the mth shell is
defined to be
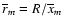 ,
where
,
where
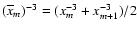 .
The density of the
mth shell is then the value given by Eq. (2) at
.
The density of the
mth shell is then the value given by Eq. (2) at
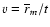 .
.
The model H atom is that used in the one-point consistency test in
Sect. 5.2 of Paper I. Thus there are 15 levels, with level 15 being the H+ continuum  .
The 14 bound levels correspond to
principal quantum numbers i = 1-14 and have consolidated statistical
weights
gi = 2i2.
.
The 14 bound levels correspond to
principal quantum numbers i = 1-14 and have consolidated statistical
weights
gi = 2i2.
Transition probabilities and photoionization cross sections for
hydrogen can of course be computed with arbitrary accuracy. Accordingly,
the oscillator strengths for bound-bound (b-b) transitions are derived from
an accurate look-up table. But the continuous absorption coefficient
is simplified by setting Gaunt factors = 1. Thus, the cross section
for photoionization from level i is
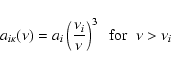 |
(3) |
where ai is the cross section at the ionization threshold frequency 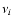 .
.
In the following three sections, a detailed account is given of how the
internal radiation field in the SN's envelope is derived using the macro-atom
formalism of Paper I. This MC calculation is subsequently embedded in an
outer iteration loop (Sect. 6.5) in the search for the NLTE solution.
A random number generator is essential for every MC code.
In this investigation, the routine ran2 from Numerical
Recipes (Press et al. 1992) is used, but with minor changes to convert to
double precision. Independent tests confirm the high quality of sequences of
random numbers created with this routine.
In the rest of this paper, the variable z denotes a random
number sampling a uniform distribution in the interval (0,1) and thus
indicates a call to ran2 in the MC code.
In Paper I, three formulations of the macro-atom
technique were presented. Two concerned alternative treatments of stimulated
emission; and the third, moving media in the Sobolev limit. Here,
in view of the large velocity gradients
in a SN envelope, we treat line formation in the Sobolev
approximation and so follow the formulation presented in Sect. 4.3
of Paper I.
Although accuracy is not of concern in this paper, it is
nevertheless of
interest that Duschinger et al. (1995) find that, in treating the
formation of hydrogen
lines in type II SNe, the Sobolev approximation is as accurate as the
comoving frame method.
Because of the envelope's large optical depth in the Lyman
continuum, an r-packet in that continuum will propagate a negligible
distance before it undergoes a bound-free (b-f) absorption. Accordingly,
a useful economy of computational effort is
obtained by assuming that such packets are
re-absorbed at the point of emission. This
is the familiar "on-the-spot'' approximation commonly used for models of
photoionized nebulae (e.g., Osterbrock 1974). Moreover, as for such models,
this approximation is implemented for the dominant source of
r-packets with
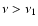 by setting
by setting
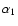 and
and
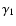 ,
the ground state
recombination and photoionization coefficients, to zero. Of course, Lyman
continuum r-packets can in principle also be emitted by f-f emission and
by recombinations
to excited levels. Such packets if they occur are re-absorbed in situ by
activating a macro-atom to state
,
the ground state
recombination and photoionization coefficients, to zero. Of course, Lyman
continuum r-packets can in principle also be emitted by f-f emission and
by recombinations
to excited levels. Such packets if they occur are re-absorbed in situ by
activating a macro-atom to state 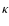 .
.
The above approximation effectively imposes an upper limit
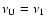 on the MC radiation field. In a second approximation,
a lower limit
on the MC radiation field. In a second approximation,
a lower limit
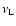 is also imposed. The reason for this is the
is also imposed. The reason for this is the 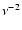 dependence of f-f absorption as
dependence of f-f absorption as
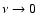 ,
which results in
occasional jumps in estimates of
,
which results in
occasional jumps in estimates of
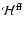 ,
the f-f heating rate, when
an r-packet is
emitted with
,
the f-f heating rate, when
an r-packet is
emitted with
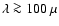 m. The limit
m. The limit
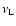 eliminates such
jumps at the price of a slightly biased estimate of
eliminates such
jumps at the price of a slightly biased estimate of
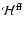 .
.
The chosen lower limit
 ,
the ionization
threshold of the highest bound level i = 14. To ensure that r-packets
are not emitted with
,
the ionization
threshold of the highest bound level i = 14. To ensure that r-packets
are not emitted with
 ,
we set oscillator strengths
fji = 0 if
,
we set oscillator strengths
fji = 0 if
 and also exclude
and also exclude
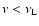 when
sampling the f-f emissivity function.
when
sampling the f-f emissivity function.
Note that, in order to avoid loss of generality, these devices for
imposing frequency limits are ignored in all subsequent formulae.
A further approximation is the neglect in the transfer theory of all
terms of O(v/c) except for the Doppler effect (McCrea & Mitra 1936;
Lucy 1971, 1999b). But apart from time-delay, it is quite
straightforward to include relativistic effects in MC codes
(Mazzali & Lucy 1993).
The NLTE solution must be obtained iteratively and so starting
values are required for the basic variables. For every
iteration except the first, the previous iteration's radiation
field 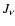 is available, as also are the
corresponding temperatures T and level-populations ni.
For the first iteration, initial guesses are required for
these quantities.
is available, as also are the
corresponding temperatures T and level-populations ni.
For the first iteration, initial guesses are required for
these quantities.
The initial mean intensity of the radiation field
in the Balmer and higher continua is taken to be
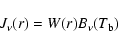 |
(4) |
where the dilution factor
![$W = \frac{1}{2} \left[1-\sqrt{1-x^{2}}\right]$](/articles/aa/full/2003/19/aa3550/img42.gif) .
.
The lower-boundary temperature 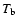 ,
which also determines the
frequency
distribution of r-packets launched into D at r = R - see Eq. (1), is
initiated at
,
which also determines the
frequency
distribution of r-packets launched into D at r = R - see Eq. (1), is
initiated at
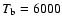 K.
K.
With the radiation field specified, values of T,
ni and 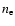 in each shell
could be obtained by
imposing the constraints of statistical and thermal equilibrium as
described in Sect. 6. Instead, the simpler and cruder option is followed of
assuming an
isothermal stratification with T =5000 K and then obtaining the
initial ni and
in each shell
could be obtained by
imposing the constraints of statistical and thermal equilibrium as
described in Sect. 6. Instead, the simpler and cruder option is followed of
assuming an
isothermal stratification with T =5000 K and then obtaining the
initial ni and 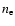 from the Saha and Boltzmann
formulae.
from the Saha and Boltzmann
formulae.
With the current estimates of 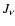 ,
T and ni,
the MC transition probabilities are computed for the
next simulation of the radiation field. Following an e-packet's
capture by a macro-atom, these probabilities determine stochastically the
characteristics of the subsequently-emitted e-packet.
,
T and ni,
the MC transition probabilities are computed for the
next simulation of the radiation field. Following an e-packet's
capture by a macro-atom, these probabilities determine stochastically the
characteristics of the subsequently-emitted e-packet.
The MC transition probabilities defined in Paper I and in this
paper involve ratios of the rates of various radiative and collisional
processes. As in Paper I, the formulae for such rates always refer to unit
volume.
Adopting the notation of Paper I, we define
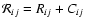 to be the total rate of the
transition
to be the total rate of the
transition
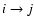 ,
with Rij and Cij denoting
radiative and collisional rates. Also, except where noted,
the summation convention of Paper I is assumed. Thus suffixes
,
with Rij and Cij denoting
radiative and collisional rates. Also, except where noted,
the summation convention of Paper I is assumed. Thus suffixes 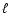 and uindicate summations over all levels <i and all levels >i,
respectively.
and uindicate summations over all levels <i and all levels >i,
respectively.
The probability that a
macro-atom in state i emits an r-packet and thus de-activates is then
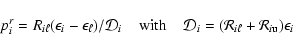 |
(5) |
where
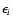 is the excitation energy of
level i.
The corresponding probability for the emission of a k-packet is
is the excitation energy of
level i.
The corresponding probability for the emission of a k-packet is
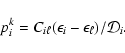 |
(6) |
In addition to the options of emitting an r- or a k-packet,
a macro-atom in state i can spontaneously jump to any other state j. Moreover, such internal transitions occur without the absorption or
emission of an e-packet. The probabilities of internal transitions to
the particular upper or lower states u and 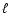 are
are
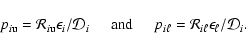 |
(7) |
The above options for leaving state i are complete; consequently,
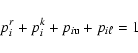 |
(8) |
as may readily be demonstrated.
In order to compute these MC transition probabilities, the rates Rij and Cij must be specified.
The rates of excitation and de-excitation due to collisions
by thermal electrons are
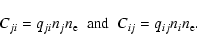 |
(9) |
The rates of collisional ionization and recombination have the same form,
except that the latter, being a three-body process, is 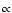
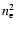 .
.
For excitations, the coefficient qjiis computed with van Regemorter's (1962) approximate formula and the
inverse coefficient qij by detailed balancing. For collisional
ionizations, the coefficient
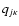 is evaluated with the
approximate formula given by Mihalas (1978, Eq. (5-79)), with the inverse
coefficient
is evaluated with the
approximate formula given by Mihalas (1978, Eq. (5-79)), with the inverse
coefficient
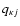 again obtained by detailed balancing.
again obtained by detailed balancing.
The radiative bound-bound (b-b) rates are computed
in the Sobolev approximation as discussed earlier. Thus, with stimulated
emissions treated as negative absorptions,
the radiative rates
between bound level i and a lower level j are
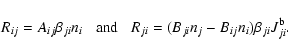 |
(10) |
Here the mean intensity
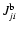 refers to the far blue wing of the
transition
refers to the far blue wing of the
transition
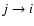 ,
and
,
and
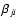 is the Sobolev escape probability,
given by
is the Sobolev escape probability,
given by
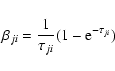 |
(11) |
where 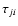 is the transition's Sobolev optical depth. In the
special case of homologous expansion,
is the transition's Sobolev optical depth. In the
special case of homologous expansion,
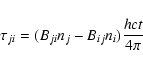 |
(12) |
with t being the elapsed time since the SN exploded.
For the first iteration, he mean intensities
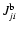 are from Eq. (4). For subsequent iterations, they are evaluated from
the MC radiation field - see Sect. 6.2.
are from Eq. (4). For subsequent iterations, they are evaluated from
the MC radiation field - see Sect. 6.2.
The radiative processes coupling bound levels to the continuum are
photoionizations and radiative recombinations. The rate coefficient for
spontaneous recombinations to level i is (e.g., Mihalas 1978, p. 131)
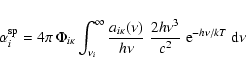 |
(13) |
with
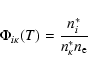 |
(14) |
where an asterisk indicates the level's LTE population at the given Tand  .
The corresponding rate coefficient for stimulated recombinations
.
The corresponding rate coefficient for stimulated recombinations
 is
is
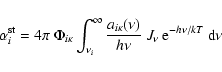 |
(15) |
and that for photoionizations
 is
is
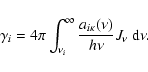 |
(16) |
In terms of the above, the total recombination coefficient for level i is
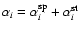 .
.
If we treat stimulated recombinations as negative photoionizations,
the radiative rates coupling i and  are
are
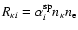 and
and
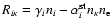 .
This
latter rate may be written as
.
This
latter rate may be written as
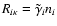 ,
where
the corrected photionization coefficient
,
where
the corrected photionization coefficient
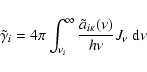 |
(17) |
is expressed in terms an absorption cross section
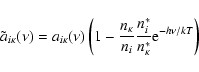 |
(18) |
which incorporates the NLTE correction factor for stimulated emissions.
The rates at which b-f and f-b transitions absorb and emit
radiant energy are needed in the course of the calculation. These can
conveniently be expressed in terms of modified photoionization and
recombination coefficients. Thus the rate at which
photoionizations from level i remove energy from the radiation field
is
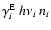 ,
where
,
where
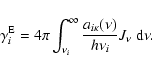 |
(19) |
Comparison with Eq. (16) shows that this modified coefficient
is obtained from the conventional one by changing 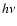 to
to 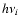 in the integrand's denominator.
in the integrand's denominator.
Similarly, the corresponding rate at which spontaneous
recombinations to level i add energy to the radiation field is
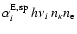 ,
where
,
where
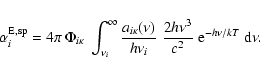 |
(20) |
This modified coefficient
is again obtained from the conventional one (Eq. (13))
by changing 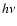 by
by 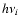 in the integrand's denominator.
in the integrand's denominator.
Following the same procedure, the modified coefficients
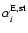 and
and
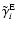 are also defined.
Thus stimulated recombinations to level i emit radiant energy at
the rate
are also defined.
Thus stimulated recombinations to level i emit radiant energy at
the rate
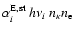 .
But when treated as negative photoionizations, these
stimulated recombinations reduce the rate at which photoionizations
from level i absorb radiant energy to
.
But when treated as negative photoionizations, these
stimulated recombinations reduce the rate at which photoionizations
from level i absorb radiant energy to
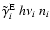 .
.
In terms of the above, the total rate at which recombinations to
level i emit radiant energy is
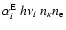 ,
where
,
where
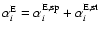 .
.
For the first iteration, the coefficients
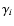 ,
,
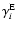 ,
,
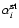 and
and
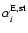 are derived by
numerical integration with
are derived by
numerical integration with 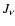 from Eq. (4). For subsequent
iterations, they are evaluated using the MC radiation field - see Sect. 6.2.
In terms of these coefficients, the corrected photionization
coefficient
from Eq. (4). For subsequent
iterations, they are evaluated using the MC radiation field - see Sect. 6.2.
In terms of these coefficients, the corrected photionization
coefficient
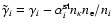 and correspondingly for
and correspondingly for
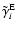
This MC technique directly models the flow of energy through the
domain D by computing
the interaction histories of numerous indivisible e-packets. In
consequence of these interactions, an e-packet is sometimes an
r-packet and at other times a k-packet. Accordingly, in this section,
the probabilistic rules governing the emission and absorption
of both r- and k-packets are developed.
In the absence of non-radiative heating in D, the desired solution
satisfies the constraint of radiative equilibrium in the co-moving frame at
every point in D. This constraint is rigorously incorporated into the
macro-atom formalism
by not allowing active macro-atoms to appear or disappear spontaneously
within D.
This then implies that every e-packet's interaction history both
begins and ends as an r-packet crossing a boundary of D
(Sect. 7.1, Paper I). Accordingly, in the context of a
spherically-symmetrical SN envelope, the creation
of r-packets corresponds to a sampling of
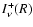 given
by Eq. (1).
given
by Eq. (1).
In the previous SN and stellar wind codes, the initial
energies
 of the packets were equal, independent of frequency.
But now, in order
that the weak radiation field between L
of the packets were equal, independent of frequency.
But now, in order
that the weak radiation field between L and the Lyman limit is well
represented, r-packets are created in equal numbers in equal intervals of
and the Lyman limit is well
represented, r-packets are created in equal numbers in equal intervals of
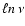 ,
with energies assigned in accordance with
black body emission at
,
with energies assigned in accordance with
black body emission at 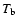 .
.
Despite r-packets no longer having equal initial energies, MC
estimators for integrals of the radiation field can be
cast in familiar form if we take
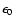 to be the unit
adopted for measuring the energies of the packets.
A convenient choice is defined by the equation
to be the unit
adopted for measuring the energies of the packets.
A convenient choice is defined by the equation
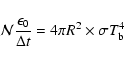 |
(21) |
where 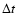 is the
interval simulated by the MC experiment and
is the
interval simulated by the MC experiment and 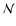 is the
number of r-packets
launched across the lower boundary r = R in time
is the
number of r-packets
launched across the lower boundary r = R in time 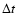 .
.
Now consider an r-packet representing emission by the lower
boundary in the interval
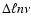 at
at  during time
during time 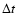 .
Since the flux
transported by
.
Since the flux
transported by
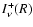 in this interval is
in this interval is
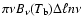 ,
this packet's energy in the
co-moving frame is given by
,
this packet's energy in the
co-moving frame is given by
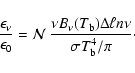 |
(22) |
A total of 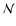 packets with fractional energies given by
Eq. (22) are created
uniformly in
packets with fractional energies given by
Eq. (22) are created
uniformly in
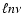 in the frequency interval
in the frequency interval
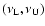 - see Sect. 3.3.
- see Sect. 3.3.
Notice that the values of
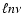 are not obtained by
random sampling. This is the one point in the calculation where
stratified sampling can readily and safely be used to limit MC
noise.
are not obtained by
random sampling. This is the one point in the calculation where
stratified sampling can readily and safely be used to limit MC
noise.
The r-packets must also have their initial direction cosines 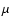 specified. Assuming zero limb-darkening for emission at the lower
boundary - see Eq. (1), we randomly sample this limb-darkening law by
taking
specified. Assuming zero limb-darkening for emission at the lower
boundary - see Eq. (1), we randomly sample this limb-darkening law by
taking
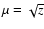 .
The packet's initial rest energy is then
.
The packet's initial rest energy is then
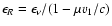 .
.
A macro-atom can be activated by a k-packet or an
r-packet. The MC transition probabilities
defined in Sect. 3.5 are then applied until the macro-atom de-activates.
This occurs
with the emission of a k-packet or an r-packet. If an r-packet is
emitted, the next step is to assign  .
The relevant procedure depends on whether
de-activation occurred from the continuum state or from a discrete state.
.
The relevant procedure depends on whether
de-activation occurred from the continuum state or from a discrete state.
In this case, the emitted r-packet belongs to an emission line
arising from atomic level i. One of these lines must therefore be selected
randomly, with
due weight given to the lines' emissivities.
Since the total emissivity of the lines
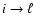 is
is
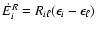 ,
where
the
,
where
the
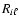 are from Eq. (10),
the selection probability for the line
are from Eq. (10),
the selection probability for the line
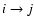 is
is
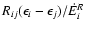 .
.
If the line thus randomly selected is
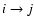 ,
the
,
the  of the emitted r-packet is simply the transition's
rest frequency
of the emitted r-packet is simply the transition's
rest frequency
 .
Note that because we are using the Sobolev approximation in
the narrow-line limit, no sampling of an emission profile is required.
.
Note that because we are using the Sobolev approximation in
the narrow-line limit, no sampling of an emission profile is required.
In this case,
the emitted r-packet's  is obtained by sampling
the energy distributions of the spontaneous recombination continua
(Sect. 4.2.3, Paper I). This can be done by first selecting a continuum and
then selecting a
is obtained by sampling
the energy distributions of the spontaneous recombination continua
(Sect. 4.2.3, Paper I). This can be done by first selecting a continuum and
then selecting a  in that continuum.
in that continuum.
The emissivity due to spontaneous recombinations to level i is
(cf. Eq. (13))
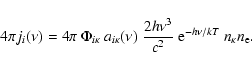 |
(23) |
Substituting for
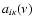 from Eq. (3) and integrating from
from Eq. (3) and integrating from  to
to 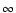 ,
we find that the integrated emissivity of the
,
we find that the integrated emissivity of the
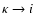 continuum is
continuum is
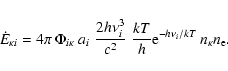 |
(24) |
The selection probability for emission in
the
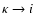 continuum is therefore
continuum is therefore
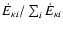 .
.
If the selected continuum is
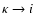 ,
the
next step is to sample its energy distribution. The
emitted r-packet's
,
the
next step is to sample its energy distribution. The
emitted r-packet's  is thus the solution of the equation
is thus the solution of the equation
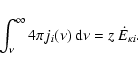 |
(25) |
Substitution from Eqs. (23) and (24) reduces this equation to the simple
formula
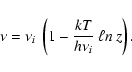 |
(26) |
Note that r-packets emitted by macro-atoms de-activating from
state 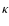 represent only the loss of ionization energy -
see Sect. 5.2 and Fig. 4 in Paper I. But recombination emission also results in
the loss of
thermal energy. This loss is represented by (some of) the
conversions of k-packets into r-packets - see Sect. 4.3.2 below.
represent only the loss of ionization energy -
see Sect. 5.2 and Fig. 4 in Paper I. But recombination emission also results in
the loss of
thermal energy. This loss is represented by (some of) the
conversions of k-packets into r-packets - see Sect. 4.3.2 below.
The MC transition probabilities defined in Paper I model the effect of atomic
levels on the frequency redistribution of absorbed radiant energy.
Another set of probabilities must now be defined to model the corresponding
effect of interactions with the thermal pool. In this formalism,
such interactions are represented by the emission and absorption of
k-packets.
Note that in developing probabilistic rules for k-packets, we
assume that b-f and f-f absorptions as well as collisional de-excitations and
recombinations are all followed by an instantaneous re-adjustment of
the thermal motions to a Maxwell velocity distribution. Accordingly,
when considering the elimination of k-packets, we use rate coefficients
that assume a Maxwell distribution for the thermal electrons.
The interactions creating k-packets correspond to the
mechanisms heating the gas.
Collisional de-excitations and recombinations convert excitation and
ionization energy into heat. These processes are represented in this
formalism as
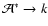 - i.e., by the
emission of a k-packet by an active macro-atom - see Eq. (6).
- i.e., by the
emission of a k-packet by an active macro-atom - see Eq. (6).
A second heating mechanism is the conversion of radiant energy into
heat by f-f absorptions. In this formalism, this corresponds to
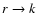 - i.e., to the direct conversion of an r-packet into
a k-packet without the mediation of a macro-atom.
- i.e., to the direct conversion of an r-packet into
a k-packet without the mediation of a macro-atom.
A third heating mechanism is the conversion of radiant energy into
heat by b-f absorptions. For this mechanism, an extended discussion is
necessary since not all absorbed energy appears as heat.
In terms of the modified photoionization coefficient defined in
Sect. 3.6, the rate at which b-f transitions from level iabsorb radiant energy is
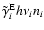 .
But each photoionization raises the ionization energy by
.
But each photoionization raises the ionization energy by
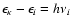 .
Accordingly, from the
total absorbed rate, the amount
.
Accordingly, from the
total absorbed rate, the amount
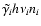 is used in ionizing the atoms, with only the remainder
is used in ionizing the atoms, with only the remainder
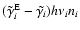 available to heat the gas.
available to heat the gas.
The existence of these two channels might
suggest that an r-packet undergoing a b-f absorption should be split.
But this would lose the advantages of working with indivisible packets
(Paper I, Sect. 1). Instead, therefore, the absorbed energy is assigned
randomly to one or other of the channels. Thus, with probability
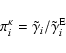 |
(27) |
the r-packet activates a macro-atom to its continuum state 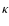 -
i.e.,
-
i.e.,
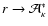 .
Alternatively, with probability
.
Alternatively, with probability
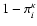 ,
the r-packet converts directly into a k-packet - i.e.,
,
the r-packet converts directly into a k-packet - i.e.,
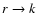 .
In the first case, all of
the r-packet's energy is converted into ionization energy; in the
second, all is contributed to the thermal pool.
.
In the first case, all of
the r-packet's energy is converted into ionization energy; in the
second, all is contributed to the thermal pool.
Summing over all bound states, we find that the probability that a
b-f absorption of an r-packet with frequency  results in the creation
of a k-packet is
results in the creation
of a k-packet is
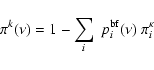 |
(28) |
where
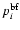 is the probability that the b-f absorption occurred from
level i. Now, since the macroscopic b-f absorption coefficient
is the probability that the b-f absorption occurred from
level i. Now, since the macroscopic b-f absorption coefficient
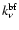 is given by
is given by
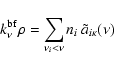 |
(29) |
where the corrected cross section
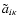 is defined by
Eq. (18), the required probability
is defined by
Eq. (18), the required probability
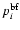 is evidently
is evidently
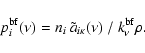 |
(30) |
The probabilities defined in this subsection are 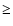 0 if
0 if
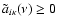 for all
for all  .
From Eq. (18), we see
that this inequality is violated as
.
From Eq. (18), we see
that this inequality is violated as
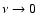 if
if
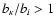 ,
where
bi = ni/ni* is the departure
coefficient for level i. In the numerical tests of Sect. 7, minor violations
of the condition
,
where
bi = ni/ni* is the departure
coefficient for level i. In the numerical tests of Sect. 7, minor violations
of the condition
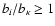 occur for high levels of the model
H atom, and these are probably due to the neglect of the recombinations into
levels i > 14 and therefore of the subsequent cascade contributions to the
included levels. To avoid negative probabilities when this happens, we
set
occur for high levels of the model
H atom, and these are probably due to the neglect of the recombinations into
levels i > 14 and therefore of the subsequent cascade contributions to the
included levels. To avoid negative probabilities when this happens, we
set
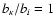 in Eq. (18) if
in Eq. (18) if
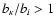 .
.
On the assumption that advection and conduction of thermal energy are
negligible compared with radiative transport (but note the possibilities of
generalization), a k-packet is converted in situ back into
an r-packet, either directly (
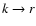 )
or indirectly
(
)
or indirectly
(
 ). The
interactions eliminating k-packets correspond to the mechanisms cooling
the gas, and their selection probabilities are determined by the mechanisms'
cooling rates.
). The
interactions eliminating k-packets correspond to the mechanisms cooling
the gas, and their selection probabilities are determined by the mechanisms'
cooling rates.
Collisional excitations and ionizations convert heat
into excitation and ionization energy. The total cooling rate provided by
this mechanism is
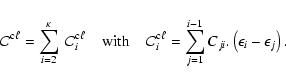 |
(31) |
A second cooling mechanism is the conversion of heat into radiant
energy by f-f emission. The cooling rate in this case
(e.g., Osterbrock 1974, p. 44) is
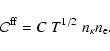 |
(32) |
With the mean Gaunt factor set =1, the coefficient
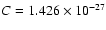 (cgs).
(cgs).
A third cooling mechanism is the conversion of heat into radiant
energy by f-b emission. The rate at which spontaneous recombinations
 convert thermal and ionization energy into radiant energy is
convert thermal and ionization energy into radiant energy is
 - see Sect. 3.6. But
each such recombination releases
- see Sect. 3.6. But
each such recombination releases 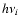 of ionization energy, which is
therefore being radiated at the rate
of ionization energy, which is
therefore being radiated at the rate
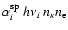 .
Subtracting this from the
previous expression and summing over bound states, we find that the rate
at which heat is radiated by spontaneous f-b
transitions is
.
Subtracting this from the
previous expression and summing over bound states, we find that the rate
at which heat is radiated by spontaneous f-b
transitions is
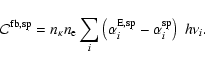 |
(33) |
With cooling rates thus specified, the selection probabilities are
as follows: a k-packet is removed by a f-b transition (
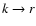 )
with probability
)
with probability
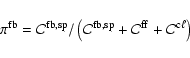 |
(34) |
by a f-f process (
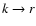 )
with probability
)
with probability
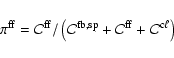 |
(35) |
and by a collisional process with probability
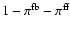 .
In this
last case, the k-packet activates a macro-atom
(
.
In this
last case, the k-packet activates a macro-atom
(
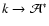 )
and so is not directly
converted into an r-packet.
)
and so is not directly
converted into an r-packet.
Note that the quantity subtracted in Eq. (33), namely the rate
of loss of ionization energy, is represented in this MC procedure by
macro-atoms de-activating from state 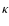 (Sect. 4.2.2). Also
cooling by stimulated recombinations
does not appear in the above formulae because these recombinations, treated
as negative photoionization, are allowed for when creating k-packets
(Sect. 4.3.1).
(Sect. 4.2.2). Also
cooling by stimulated recombinations
does not appear in the above formulae because these recombinations, treated
as negative photoionization, are allowed for when creating k-packets
(Sect. 4.3.1).
The MC model of the radiation field in the SN envelope is built up from the
trajectories of 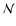 individual r-packets,
starting from their launch into D at r=R and ending with their
exit from D, either by escaping to
individual r-packets,
starting from their launch into D at r=R and ending with their
exit from D, either by escaping to 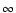 or by re-crossing the lower boundary.
or by re-crossing the lower boundary.
As an r-packet propagates in D, it will typically undergo
numerous geometrical and physical "events''. The geometrical events
are simply crossings of the boundaries of the 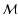 constant-density shells.
But the more important physical events constitute the MC technique's
treatment of the interactions of radiation and matter.
constant-density shells.
But the more important physical events constitute the MC technique's
treatment of the interactions of radiation and matter.
In describing how the packets' trajectories are computed, it suffices
to explain how to find the next event along one packet's trajectory. Thus,
we now
suppose that an r-packet has just undergone event n in its
propagation history and that this occurred in shell m. The task now
is first to find the location and nature
of event n+1 and then to compute the frequency  and direction of
propagation of
the r-packet that emerges from this event.
and direction of
propagation of
the r-packet that emerges from this event.
Immediately following event n, the macroscopic coefficients
of continuum absorption
(
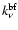 ,
,
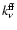 )
and scattering (
)
and scattering (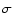 )
must be computed since the r-packet is either in a new shell or has
changed its
)
must be computed since the r-packet is either in a new shell or has
changed its  .
.
The b-f coefficient, corrected for stimulated
emission, is given by Eq. (18), where
the ni are the current estimates of the NLTE level populations in
shell m. The f-f coefficient
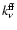 is calculated with the standard formula but with mean Gaunt
factor = 1, in accordance with the corresponding simplification for
Eq. (3).
is calculated with the standard formula but with mean Gaunt
factor = 1, in accordance with the corresponding simplification for
Eq. (3).
If s is distance from event n measured along the packet's
trajectory
and 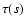 is the corresponding optical depth, then
the pathlength
is the corresponding optical depth, then
the pathlength 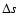 between events n
and n+1 is determined by the equation
between events n
and n+1 is determined by the equation
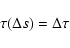 |
(36) |
where the beam's exponential decay with optical depth is randomly sampled
by taking
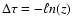 .
.
Continuum and line processes both contribute to 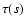 .
The
continuum contibution is approximately
.
The
continuum contibution is approximately
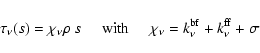 |
(37) |
where  is the packet's frequency immediately following
event n. Notice that the small changes in the extinction coefficient seen
by the packet as its
is the packet's frequency immediately following
event n. Notice that the small changes in the extinction coefficient seen
by the packet as its  decreases along the trajectory between
events n and n+1 are neglected. This is justified since these changes
decreases along the trajectory between
events n and n+1 are neglected. This is justified since these changes
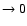 as
as
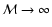 .
.
The contribution of lines to 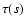 is computed with the Sobolev
approximation in the narrow-line limit, according to which a line with
Sobolev optical depth
is computed with the Sobolev
approximation in the narrow-line limit, according to which a line with
Sobolev optical depth 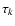 attenuates an incident
beam by the factor e
attenuates an incident
beam by the factor e
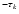 at the point where resonance
occurs.
Thus
at the point where resonance
occurs.
Thus 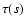 undergoes discontinuous increments
undergoes discontinuous increments 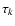 at the points sk where the packet's
frequency
at the points sk where the packet's
frequency 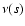 equals one of the rest frequencies
equals one of the rest frequencies 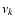 of the b-b
transitions. Accordingly,
of the b-b
transitions. Accordingly,
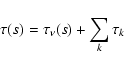 |
(38) |
where the summation extends over all sk in the
interval (0,s). Moreover, at each sk,
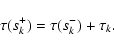 |
(39) |
The above prescription for locating event n+1
applies only if it occurs within shell m. If Eq. (36)
is not satisfied in shell m, event n+1 is geometrical, and
the pathlength 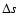 is then simply the distance from event n to the
point where the trajectory crosses into a neighbouring shell.
is then simply the distance from event n to the
point where the trajectory crosses into a neighbouring shell.
If event n+1 occurs within shell m then it is
physical, due to either continuum extinction or a line absorption.
The former is indicated if
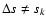 ;
the latter otherwise.
;
the latter otherwise.
If the event is a continuum extinction, we decide between
the three contributing mechanisms
using a single random number: the event is an
electron scattering if
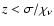 ;
failing this, the event is a
b-f absorption if
;
failing this, the event is a
b-f absorption if
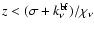 ;
failing this, the
event is a f-f absorption.
;
failing this, the
event is a f-f absorption.
Event n+1 is absorption in line k if
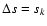 .
But since
.
But since 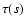 has a discontinuity at sk, this solution
of Eq. (36) is actually recognized by finding that
has a discontinuity at sk, this solution
of Eq. (36) is actually recognized by finding that
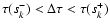 .
.
With the nature of event n+1 determined, the next task is
to assign a frequency to the emitted r-packet.
If event n+1 is geometrical, the r-packet is simply
continuing its existing flight path into the new shell, and so the  at
the beginning of the "new'' trajectory is identical to the
at
the beginning of the "new'' trajectory is identical to the  at the end of
the "previous'' trajectory, namely the value at the boundary crossing.
at the end of
the "previous'' trajectory, namely the value at the boundary crossing.
On the other hand, if event n+1 is physical, the nature of the
event determines the procedure to be followed in assigning  .
.
With electron scatterings treated as coherent in the comoving frame,
the scattered r-packet's  is identical to that of the incident packet.
is identical to that of the incident packet.
If event n+1 is absorption by the transition
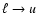 ,
the immediate result is a macro-atom in state u - i.e.
,
the immediate result is a macro-atom in state u - i.e.
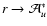 .
The next step therefore is
the repeated application of
the transition probabilities of Sect. 3.5 until the macro-atom
de-activates. This was discussed at length in Paper I and
specifically
illustrated in Sect. 5.5 of that paper with the 15-level H atom used here.
.
The next step therefore is
the repeated application of
the transition probabilities of Sect. 3.5 until the macro-atom
de-activates. This was discussed at length in Paper I and
specifically
illustrated in Sect. 5.5 of that paper with the 15-level H atom used here.
The macro-atom de-activates with the emission of either a k-packet or an r-packet. In the former case, the k-packet is eliminated
in situ as described in Sect. 4.3.2.
If the macro-atom de-activates with the emission of an r-packet,
selection of  depends on whether it was emitted from the continuum state
depends on whether it was emitted from the continuum state 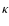 or from one of the bound states
or from one of the bound states
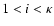 .
These cases were
both discussed in Sect. 4.2, where the selection procedures followed in
assigning
.
These cases were
both discussed in Sect. 4.2, where the selection procedures followed in
assigning  are given.
are given.
If event n+1 was a f-f absorption, the immediate result is a k-packet
which then in situ either converts into an r-packet or excites
a macro-atom.
The conversion
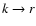 occurs by f-b emission with probability
occurs by f-b emission with probability
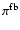 or by f-f emission
with probability
or by f-f emission
with probability
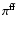 (Sect. 4.3.2). For f-b emission, the selection
of
(Sect. 4.3.2). For f-b emission, the selection
of  for the emergent r-packet is the two step procedure described in
Sect. 4.2.2.
for the emergent r-packet is the two step procedure described in
Sect. 4.2.2.
For f-f emission,  is selected by sampling this mechanism's
emissivity function - i.e., by solving the equation
is selected by sampling this mechanism's
emissivity function - i.e., by solving the equation
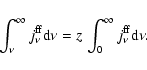 |
(40) |
If the  -dependence of the velocity-averaged Gaunt factor is
neglected,
-dependence of the velocity-averaged Gaunt factor is
neglected,
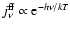 and the solution is
and the solution is
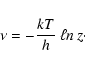 |
(41) |
Besides these two direct
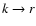 conversions, there is
alternatively the indirect conversion
conversions, there is
alternatively the indirect conversion
 ,
which occurs
with probability
,
which occurs
with probability
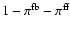 and is due to collisional cooling.
In this case, the macro-atom is activated to state i with probability
and is due to collisional cooling.
In this case, the macro-atom is activated to state i with probability
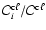 - see Eq. (31). Application of
the MC transition
probabilities as in Sect. 5.4.2 then leads eventually to the emission
of an r-packet.
- see Eq. (31). Application of
the MC transition
probabilities as in Sect. 5.4.2 then leads eventually to the emission
of an r-packet.
If event n+1 is a b-f absorption, the immediate result is either a
k-packet (Sect. 4.3.1) or a
macro-atom in state 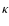 .
The selection probability
is
.
The selection probability
is
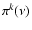 for the former and
for the former and
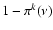 for the latter, where
for the latter, where  is the frequency of the incident r-packet.
is the frequency of the incident r-packet.
If this selection results in a macro-atom in state 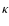 ,
the
MC transition rules are applied as described in Sect. 5.4.2 until an
r-packet is emitted. On the other hand, if the result is a k-packet, it
converts in situ into an r-packet as described in Sect. 5.4.3.
,
the
MC transition rules are applied as described in Sect. 5.4.2 until an
r-packet is emitted. On the other hand, if the result is a k-packet, it
converts in situ into an r-packet as described in Sect. 5.4.3.
Re-emission following a physical event is assumed to occur
isotropically in the matter frame, so the new direction cosine in every
case is
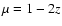 .
For electron scattering, this is an approximation. But isotropic
emission is exact for
thermal processes - i.e., for f-f and f-b emissions. It is also exact for
the Sobolev treatment of b-b emission
in a homologously expanding flow since there is then no
kinematically-preferred direction.
.
For electron scattering, this is an approximation. But isotropic
emission is exact for
thermal processes - i.e., for f-f and f-b emissions. It is also exact for
the Sobolev treatment of b-b emission
in a homologously expanding flow since there is then no
kinematically-preferred direction.
If this technique is applied to a spherically-symmetric stellar wind,
the expansion is no longer homologous and so b-b emission is angle dependent.
Specifically, the pdf to be sampled for the new direction cosine is
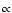
![$I_{\nu_{k}}^{r}(\mu)/\left[\mu^{2} {\rm d}v/{\rm d}r + (1 - \mu^{2}) v/r\right]$](/articles/aa/full/2003/19/aa3550/img184.gif) ,
where
,
where
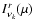 is the intensity in the line's far-red wing
of the radiation emitted by the line (Castor 1970; Lucy 1971).
is the intensity in the line's far-red wing
of the radiation emitted by the line (Castor 1970; Lucy 1971).
If
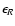 is the packet's
rest energy during its free flight prior to event n+1, then, at the event,
is the packet's
rest energy during its free flight prior to event n+1, then, at the event,
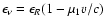 ,
where v is the velocity
at that location and
,
where v is the velocity
at that location and 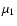 is the incident direction cosine. Now, at every event, the incident
and emergent r-packets have the same energy
is the incident direction cosine. Now, at every event, the incident
and emergent r-packets have the same energy
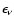 .
Accordingly,
the packet's rest energy along its free flight following event n+1is
.
Accordingly,
the packet's rest energy along its free flight following event n+1is
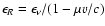 ,
where
,
where 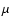 is the
new direction cosine.
is the
new direction cosine.
With the assignment of  and
and 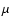 and the updating of
and the updating of
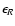 ,
the treatment of event n+1 is complete. The calculation therefore now returns to Sect. 5.1
to initiate the search for event n+2.
,
the treatment of event n+1 is complete. The calculation therefore now returns to Sect. 5.1
to initiate the search for event n+2.
The trajectories of 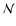 individual r-packets computed as
described in Sect. 5 collectively constitute the MC estimate of the
radiation field in D.
The next challenge is to use it to derive improved values of ni and T for each of the
individual r-packets computed as
described in Sect. 5 collectively constitute the MC estimate of the
radiation field in D.
The next challenge is to use it to derive improved values of ni and T for each of the 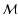 constant-density shells.
constant-density shells.
The MC estimate for the luminosity of the SN is
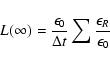 |
(42) |
where the summation is over the r-packets that escape to 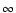 .
.
From this equation, we derive an improved scale factor
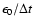 by requiring that
by requiring that 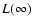 has its specified value
- see Sect. 2.2. The improved value of
has its specified value
- see Sect. 2.2. The improved value of 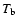 then follows from Eq. (21).
then follows from Eq. (21).
This improved scale factor is used below in computing the radiative
rates needed for the statistical and thermal equilibrium calculations. The
improved 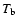 is used to determine
the initial frequency distribution of r-packets (Sect. 4.1)
at the start of the next iteration.
is used to determine
the initial frequency distribution of r-packets (Sect. 4.1)
at the start of the next iteration.
In order to use the MC radiation field to improve the values of ni and T, estimators are needed for the
radiative rate coefficients. Fortunately, efficient estimators can be
constructed with a procedure given in an earlier paper (Lucy 1999a).
In the context now of a moving atmosphere, the energy-density argument
of Lucy (1999a) applied to a local co-moving frame yields the formula
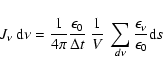 |
(43) |
where the summation is over all trajectory segments ds
in V such that the r-packets' frequencies 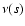 fall in the interval
fall in the interval
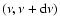 .
This equation is the building
block that allows us to construct the required estimators.
.
This equation is the building
block that allows us to construct the required estimators.
For this problem, V in Eq. (43) is the volume of one of the
spherical shells into which the envelope is discretized (Sect. 3.2). But
the estimators derived in this section are quite general: no particular
geometry or symmetry is assumed.
If we use Eq. (43) to derive an estimator
for the photoionization coefficient given by Eq. (16), the result is
a summation, with the summed quantity being
the integral of
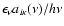 over the pathlength
over the pathlength 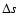 between consecutive events. But since every
pathlength is confined to a single shell,
between consecutive events. But since every
pathlength is confined to a single shell,
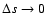 as
as
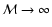 and so
and so 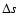 may be treated as a small
quantity.
This then implies that each
may be treated as a small
quantity.
This then implies that each 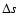 -integral can be approximated by a
one-point quadrature. With this approximation, the estimator for the
photoionization coefficient for level i is
-integral can be approximated by a
one-point quadrature. With this approximation, the estimator for the
photoionization coefficient for level i is
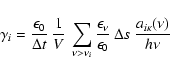 |
(44) |
where  is the packet's frequency at the mid-point of
is the packet's frequency at the mid-point of 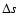 and
the summation is over all r-packets in V with
and
the summation is over all r-packets in V with
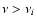 .
.
The efficiency of this estimator derives from not being
restricted to r-packets that actually cause photoionizations.
Thus its precision greatly exceeds that of an estimator based simply on
counting photoionizations in V.
In particular, this estimator returns a non-zero estimate
of
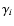 even if no r-packets cause photoionizations from level iin a given
shell, as commonly happens for the higher, less populated levels and in
the outer, less dense shells.
even if no r-packets cause photoionizations from level iin a given
shell, as commonly happens for the higher, less populated levels and in
the outer, less dense shells.
Applying the same procedure now to Eq. (15), we obtain
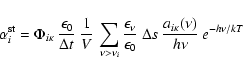 |
(45) |
as the corresponding estimator for the rate coefficient of
stimulated recombinations to level i, with  again evaluated at the
mid-point of
again evaluated at the
mid-point of 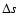 .
This estimator's efficiency
is a consequence of not being limited to r-packets that actually cause
stimulated recombinations.
.
This estimator's efficiency
is a consequence of not being limited to r-packets that actually cause
stimulated recombinations.
The above estimators refer to transitions to and from the continuum.
But statistical equilibrium also depends on the radiative rates
of b-b transitions - see Eq. (10). Thus we require an estimator for
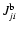 ,
the mean intensity at frequency
,
the mean intensity at frequency
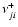 - i.e. in the far blue wing of the transition
- i.e. in the far blue wing of the transition
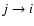 .
This can
also be derived from Eq. (43).
.
This can
also be derived from Eq. (43).
For homologous expansion, there is no kinematically-preferred
direction, and so
the rate at which the frequency 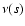 of an r-packet
in free flight decreases with distance s is independent of its direction of
propagation.
To the accuracy of this calculation - see Sect. 3.3, this rate is
of an r-packet
in free flight decreases with distance s is independent of its direction of
propagation.
To the accuracy of this calculation - see Sect. 3.3, this rate is
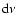 /
/
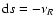 /ct. This equation gives the length ds of the
trajectory segment within which
/ct. This equation gives the length ds of the
trajectory segment within which  is in the interval
is in the interval
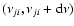 .
Substituting this value of ds into Eq. (43),
we obtain
.
Substituting this value of ds into Eq. (43),
we obtain
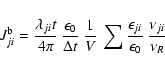 |
(46) |
as an estimator for the mean intensity at
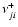 .
In this formula,
.
In this formula,
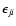 is the packet's energy at
the point where
is the packet's energy at
the point where
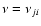 ,
and the
summation is over all r-packets in V that come into resonance with the
transition
,
and the
summation is over all r-packets in V that come into resonance with the
transition
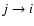 .
.
The efficiency of this estimator
derives from it not being restricted to r-packets that actually undergo
the b-b transition
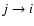 .
Accordingly, a non-zero estimate is
usually returned even when no such transitions occur in V. Evidently, the
estimate is zero only if no r-packets in V happened to come into resonance
during the MC calculation. To avoid such spurious zero estimates for
.
Accordingly, a non-zero estimate is
usually returned even when no such transitions occur in V. Evidently, the
estimate is zero only if no r-packets in V happened to come into resonance
during the MC calculation. To avoid such spurious zero estimates for
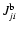 ,
a minimum value of
,
a minimum value of 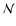 is required (Lucy 1999b).
is required (Lucy 1999b).
The above estimators refer only to the radiative rates that enter the
equations of statistical equilibrium. Further quantities are required by
the equation of thermal equilibrium. These include the coefficients
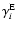 and
and
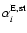 defined in Sect. 3.6. As is
evident from their definitions, estimators for these
quantities are obtained from those derived above for
defined in Sect. 3.6. As is
evident from their definitions, estimators for these
quantities are obtained from those derived above for
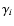 and
and
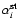 simply by changing
simply by changing 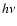 to
to 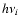 in the factors
in the factors
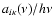 - see Eqs. (44) and (45).
- see Eqs. (44) and (45).
Finally, an estimate is also needed for the heating rate
due to f-f absorptions,
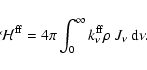 |
(47) |
If we separate out the dependence on level population by writing
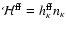 and then
again apply Eq. (43), the estimator for the coefficient is
and then
again apply Eq. (43), the estimator for the coefficient is
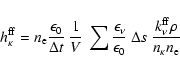 |
(48) |
where the summation is over all pathlengths in V and  is evaluated at their mid-points.
is evaluated at their mid-points.
The summations in the above estimators are accumulated in the course
of the MC simulation and are the only quantities concerning
the internal radiation field that need to be stored. When the trajectories
of all 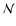 packets have been computed, the scale factor
packets have been computed, the scale factor
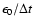 is determined as described in Sect. 6.1 and
then used to convert the summations into the required rate coefficients.
is determined as described in Sect. 6.1 and
then used to convert the summations into the required rate coefficients.
Although the accuracy of these various estimators remains to be
demonstrated, it is clear from their derivation that they are consistent.
In other words, as
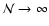 and
and
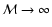 ,
they converge to the quantities being estimated.
,
they converge to the quantities being estimated.
The required solution is in statistical and thermal
equilibrium. Accordingly, following each MC calculation,
the equations representing both of these equilibria are used
simultaneously to derive improved values of ni and T throughout the
envelope. Nevertheless, it is convenient to discuss these equilibria
separately.
The equation of statistical equilibrium for level i can be
written in the form
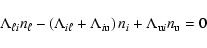 |
(49) |
where
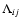 denotes the total rate coefficient for the transition
denotes the total rate coefficient for the transition
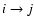 .
Specifically, for transitions between bound levels, we
have (cf. Eqs. (9) and (10)).
.
Specifically, for transitions between bound levels, we
have (cf. Eqs. (9) and (10)).
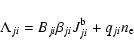 |
(50) |
for excitations
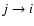 ,
and
,
and
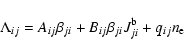 |
(51) |
for de-excitations
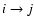 .
In addition, for transitions coupling
bound levels to the continuum, we have
.
In addition, for transitions coupling
bound levels to the continuum, we have
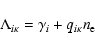 |
(52) |
for ionizations
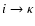 ,
and
,
and
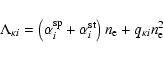 |
(53) |
for recombinations
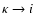 .
.
Equation (49) applies to all levels
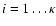 .
But since every
source term is a loss term for another level, the sum of the left hand sides
is zero, which implies that one of the equations is redundant. This leaves
.
But since every
source term is a loss term for another level, the sum of the left hand sides
is zero, which implies that one of the equations is redundant. This leaves
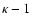 equations in the
equations in the 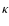 unknown level populations ni. To
make the system determinate, we impose the constraint
unknown level populations ni. To
make the system determinate, we impose the constraint
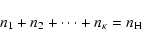 |
(54) |
where 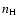 is the known number density of H atoms - see Sect. 2.1.
is the known number density of H atoms - see Sect. 2.1.
The coefficients
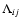 depend on
depend on
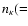
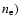 and on the ni of bound levels through
the escape probabilities
and on the ni of bound levels through
the escape probabilities
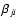 .
Accordingly, the system of equations defined by
Eqs. (49) and (54) is non-linear. But fortunately the system can be solved
iteratively with a
standard package for linear equations. Thus the coefficients are evaluated
with the current estimates of ni and then the system solved for
improved estimates. These are then used to recompute the
.
Accordingly, the system of equations defined by
Eqs. (49) and (54) is non-linear. But fortunately the system can be solved
iteratively with a
standard package for linear equations. Thus the coefficients are evaluated
with the current estimates of ni and then the system solved for
improved estimates. These are then used to recompute the
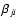 and
hence the
and
hence the
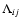 and the process repeated until convergence is
achieved.
and the process repeated until convergence is
achieved.
However, at this point a limitation in the MC approach to NLTE problems becomes apparent. The problem arises for the populations niof closely-spaced levels near the continuum. Monte Carlo sampling errors
in the estimated rates of the processes populating such levels can give rise
to level inversions, and these then prevent convergence of the above back
substitutions. To overcome this, the following stabilizing device is adopted:
for each level j,
the ni of a higher level i is replaced by
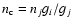 if
if
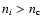 .
.
Because this problem only arises for high levels in the outermost
shells, its impact on
the MC code's prediction of the SN's line- and continuum spectrum from the UV to the mid-IR is totally negligible. Moreover, as expected, the occurrence
of these spurious inversions decreases
as the size of the MC simulation increases. For example,
with
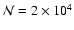 in an envelope stratified into
in an envelope stratified into
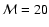 shells, inversions occurred in 13 shells starting at m = 2 and affecting
levels as low as i=6. With
shells, inversions occurred in 13 shells starting at m = 2 and affecting
levels as low as i=6. With 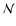 increased to
increased to
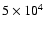 ,
inversions occur in only 5 shells starting at m = 8 and the lowest
affected level is i = 8. With a modest further increase to
,
inversions occur in only 5 shells starting at m = 8 and the lowest
affected level is i = 8. With a modest further increase to
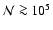 ,
inversions seldom occur. Nevertheless, problems
requiring accurate population ratios for closely-spaced levels are perhaps
best not tackled with MC methods.
,
inversions seldom occur. Nevertheless, problems
requiring accurate population ratios for closely-spaced levels are perhaps
best not tackled with MC methods.
In addition to statistical equilibrium, the required NLTE solution
must also be in thermal equilibrium. This latter equilibrium is simply the
condition that throughout the envelope
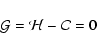 |
(55) |
where 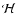 and
and 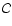 are the total heating and cooling rates,
respectively. Given the physical processes included in this
calculation, we have
are the total heating and cooling rates,
respectively. Given the physical processes included in this
calculation, we have
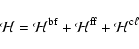 |
(56) |
and
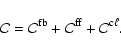 |
(57) |
In terms of the modified photoionization coefficient defined in
Sect. 3.6, the rate at which b-f transitions convert radiant energy into
thermal energy is
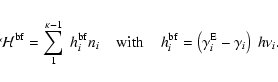 |
(58) |
The corresponding rate at which f-b transitions convert thermal energy
into radiant energy is
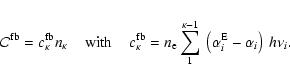 |
(59) |
The heating and cooling rates
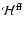 and
and
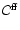 due to f-f processes have previously been
defined in Eqs. (47) and (32). The cooling rate
due to f-f processes have previously been
defined in Eqs. (47) and (32). The cooling rate
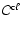 due to
collisional excitations is given by Eq. (33), and the corresponding
heating rate
due to
collisional excitations is given by Eq. (33), and the corresponding
heating rate
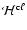 due to de-excitations is
computed similarly.
due to de-excitations is
computed similarly.
When the MC model of the internal radiation field has been computed,
the current values of a shell's level populations and temperature,
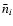 and
and 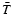 ,
do not in general correspond to thermal
equilibrium - i.e.,
,
do not in general correspond to thermal
equilibrium - i.e.,
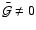 . To eliminate this residual,
we apply corrections
. To eliminate this residual,
we apply corrections
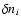 and
and 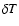 that satisfy the linearized
version of Eq. (55),
that satisfy the linearized
version of Eq. (55),
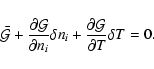 |
(60) |
But a more convenient form of this equation follows from noting that
each level's contribution to the net heating rate can be expressed in terms
of heating (hi) and cooling (ci) coefficients - see Eqs. (48), (58) and (59) -
so that
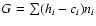 .
With this substitution, Eq. (60)
becomes
.
With this substitution, Eq. (60)
becomes
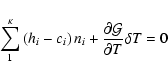 |
(61) |
where
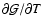 is computed by numerical
differencing, and
is computed by numerical
differencing, and
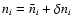 is the improved level population.
is the improved level population.
Equation (61) is one equation in 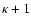 unknowns. But if
we add it to Eqs. (49) and (54), we have
unknowns. But if
we add it to Eqs. (49) and (54), we have
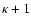 equations in the
equations in the 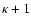 unknowns ni and
unknowns ni and 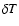 .
This combined system of equations, representing statistical and thermal
equilibrium, is solved
by repeated back substitution as described in
Sect. 6.3. With each back substitution, the coefficients
.
This combined system of equations, representing statistical and thermal
equilibrium, is solved
by repeated back substitution as described in
Sect. 6.3. With each back substitution, the coefficients
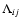 ,
hi, ci and
,
hi, ci and
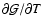 are recomputed because
of their dependences on ni,
are recomputed because
of their dependences on ni, 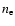 and T.
and T.
This simple iteration technique for finding ni and 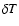 must often start far from the final solution and can
then fail due to large initial corrections.
To avoid such failures, an undercorrection factor
u = 0.8 is applied to the corrections
must often start far from the final solution and can
then fail due to large initial corrections.
To avoid such failures, an undercorrection factor
u = 0.8 is applied to the corrections
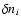 and
and 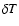 ,
and the temperature change is further limited to
,
and the temperature change is further limited to 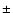
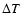 ,
with
,
with
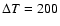 K. Moreover, if
the magnitude of the correction vector
K. Moreover, if
the magnitude of the correction vector
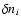 increases from one
iteration to the next, the factor u and the bound
increases from one
iteration to the next, the factor u and the bound 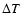 are both
decreased. With these precautions, back-substitution proves
to be a robust technique for solving the equations of statistical and thermal
equilibrium.
are both
decreased. With these precautions, back-substitution proves
to be a robust technique for solving the equations of statistical and thermal
equilibrium.
The iteration technique also fails when sampling errors'
contribution to
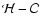 itself implies a large correction
itself implies a large correction 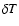 .
The only remedy in this case is to increase
.
The only remedy in this case is to increase 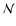 .
.
The iterations are deemed to have converged when
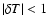 K and
K and
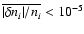 ,
where the averaging
is over levels i=1-5
because of the occasional spurious inversions of high levels (Sect. 6.3).
,
where the averaging
is over levels i=1-5
because of the occasional spurious inversions of high levels (Sect. 6.3).
When the iterations have converged to this accuracy, the typical
residuals for each shell are
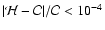 and
similarly for the agreement between the source and sink terms,
and
similarly for the agreement between the source and sink terms,
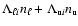 and
and
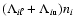 ,
for all levels i in Eq. (49).
However,
when the ni of a high level has been stabilized to avoid a spurious
inversion, the fractional departure from statistical equilibrium rises to
,
for all levels i in Eq. (49).
However,
when the ni of a high level has been stabilized to avoid a spurious
inversion, the fractional departure from statistical equilibrium rises to 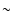 10-3.
10-3.
During the above (inner) iterations to find ni and T,
the pathlength summations of Sect. 6.2 are of necessity held fixed.
In effect, therefore, the matter in each shell is brought
into equilibrium with a fixed radiation field.
Accordingly, if the MC radiation field were now to be recomputed with the
improved ni and T, these summations would change, and so
statistical and thermal equilibrium would again be violated.
Evidently, an outer iterative loop is necessary if
convergence to the NLTE solution is to be achieved.
The scheme adopted for these outer iterations is simply to
repeatedly input the updated ni and T from Sect. 6.4 into the MC calculation of Sect. 5. These outer iterations are continued until the
changes in ni and T from one outer iteration to the next
can be attributed to MC sampling errors.
The novelty of this iterative technique is that, despite
well-documented convergence failures in various earlier applications
(see, e.g., Mihalas 1978), we are relying
on the  -iteration device of repeatedly
bringing matter into statistical and thermal equilibrium with the just-
updated MC radiation field. Indeed, these
-iteration device of repeatedly
bringing matter into statistical and thermal equilibrium with the just-
updated MC radiation field. Indeed, these 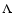 -iterations would also
fail to
converge if the radiation field were obtained by solving the
Equation of Radiative Transfer (RTE).
But in this MC scheme, the radiation field is subject at every iteration
to constraints that other iterative schemes only aim to achieve
asymptotically.
Thus, even while ni and T still depart from their equilibrium values,
the constraint of radiative equilibrium in the matter frame is
obeyed rigorously.
Moreover, the MC transition probabilities approximately
incorporate the constraints that statistical equilibrium imposes on the
frequency redistribution of absorbed radiant energy.
In effect, therefore, the scheme introduces a constrained
-iterations would also
fail to
converge if the radiation field were obtained by solving the
Equation of Radiative Transfer (RTE).
But in this MC scheme, the radiation field is subject at every iteration
to constraints that other iterative schemes only aim to achieve
asymptotically.
Thus, even while ni and T still depart from their equilibrium values,
the constraint of radiative equilibrium in the matter frame is
obeyed rigorously.
Moreover, the MC transition probabilities approximately
incorporate the constraints that statistical equilibrium imposes on the
frequency redistribution of absorbed radiant energy.
In effect, therefore, the scheme introduces a constrained
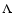 -operator that, for sufficiently large
-operator that, for sufficiently large 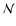 ,
generates at every iteration a radiation field
that is closer to the converged solution than would be the radiation field
generated by the RTE. The convergence of these constrained
,
generates at every iteration a radiation field
that is closer to the converged solution than would be the radiation field
generated by the RTE. The convergence of these constrained
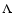 -iterations is illustrated in Sect. 7.2.
-iterations is illustrated in Sect. 7.2.
In Sects. 3-6, a detailed description has been given of how the MC model of the internal radiation field is derived and how it
is used to improve level populations and temperatures throughout
the envelope. But whether such improvements will actually result in
convergence to the NLTE solution remains to be demonstrated.
Crucial to the success or otherwise of this technique is the
accuracy of the estimators developed in Sect. 6.2.
Even with consistent estimators, the technique would have little current
interest if adequate accuracy requires simulations with
impossibly large 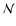 .
On the other hand, if accurate rates are
achievable with feasible values of
.
On the other hand, if accurate rates are
achievable with feasible values of 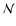 ,
then the coefficients in,
and therefore the solutions of, the equations of statistical and thermal
equilibrium will differ little from those derivable with a standard transfer
calculation.
,
then the coefficients in,
and therefore the solutions of, the equations of statistical and thermal
equilibrium will differ little from those derivable with a standard transfer
calculation.
An obvious accuracy test would be to obtain an accurate solution of a
NLTE problem using a conventional code
and then examine the convergence of MC solutions of the same problem
as 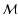 and
and 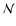 increase.
But a simpler procedure is followed here: the special case of free-streaming
r-packets allows
values of the various coefficients obtained with the MC estimators to
be compared with values obtained by numerical integration.
increase.
But a simpler procedure is followed here: the special case of free-streaming
r-packets allows
values of the various coefficients obtained with the MC estimators to
be compared with values obtained by numerical integration.
The MC code is easily modified so that r-packets
propagate without interaction.
Each packet is then emitted as before from the moving lower
boundary but thereafter conserves its
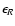 and
and 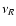 ,
while its
,
while its
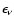 and
and  decrease along the trajectory
because of the differential expansion.
decrease along the trajectory
because of the differential expansion.
A further modification made for this free-streaming test is to
omit stratified sampling of the r-packets' frequencies at the lower
boundary - see Sect. 4.1.
Thus, the 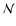 bins in
bins in
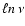 are here randomly not
uniformly sampled. By thus not benefiting from stratified sampling, the
results should be more typical of circumstances where the radiation field
is created within D rather than emitted by an artificial boundary condition.
are here randomly not
uniformly sampled. By thus not benefiting from stratified sampling, the
results should be more typical of circumstances where the radiation field
is created within D rather than emitted by an artificial boundary condition.
At radius r, the conical radiation field modelled
by this free-streaming MC calculation has specific intensity
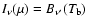 ,
where
,
where 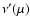 is the frequency at r = R of a photon that
reaches r with frequency
is the frequency at r = R of a photon that
reaches r with frequency  and direction cosine
and direction cosine 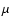 .
From this
expression for
.
From this
expression for 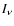 ,
the mean intensity
,
the mean intensity
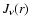 can be computed to
arbitrary accuracy by numerical integration. Such calculations carried out
at fequencies
can be computed to
arbitrary accuracy by numerical integration. Such calculations carried out
at fequencies 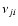 and at the mean radii
and at the mean radii
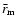 then allow the
estimator
then allow the
estimator
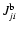 given by
Eq. (46) to be tested. Similarly,
given by
Eq. (46) to be tested. Similarly,
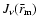 can be computed
for a grid of frequencies and then used to obtain
accurate values for the coefficients
can be computed
for a grid of frequencies and then used to obtain
accurate values for the coefficients
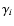 ,
,
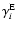 ,
,
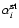 ,
,
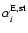 and
and
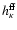 by numerical
integration, thereby testing their MC estimators from Sect. 6.2.
by numerical
integration, thereby testing their MC estimators from Sect. 6.2.
These comparisons, carried out for
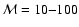 and
and
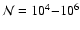 ,
support the assertion of Sect. 6.2 that these
estimators are consistent. Thus numerical experiments indicate that the
errors of the MC estimates
,
support the assertion of Sect. 6.2 that these
estimators are consistent. Thus numerical experiments indicate that the
errors of the MC estimates
 0 as
0 as  and
and
 ,
with no suggestion of
bias. But if
,
with no suggestion of
bias. But if 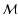 is fixed while
is fixed while
 ,
the estimators' sampling errors
,
the estimators' sampling errors
 0 but biases due to
discretization errors remain. On the other hand, if
0 but biases due to
discretization errors remain. On the other hand, if  is fixed while
is fixed while
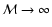 ,
biases
,
biases
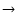 0 but sampling errors
become large, especially for the mean intensities
0 but sampling errors
become large, especially for the mean intensities
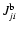 .
.
In addition to confirming the estimators' consistency, this
special case also suggests that acceptable accuracies are indeed achieved
with feasible values of 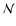 .
For example,
with
.
For example,
with
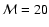 and
and
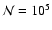 ,
the MC free-streaming
simulation requires only about 3 min computer time and yet gives reasonably
accurate coefficients. Thus, in one such simulation, the means of the
fractional and of the absolute fractional errors of the coefficients
,
the MC free-streaming
simulation requires only about 3 min computer time and yet gives reasonably
accurate coefficients. Thus, in one such simulation, the means of the
fractional and of the absolute fractional errors of the coefficients
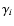 for
for
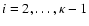 and
and
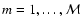 are
are
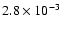 and
and
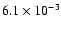 ,
respectively. These
gratifyingly small errors are a consequence of the large number of
r-packets contributing to the summation in Eq. (44) and confirm the
efficiency of estimators constructed from Eq. (43).
,
respectively. These
gratifyingly small errors are a consequence of the large number of
r-packets contributing to the summation in Eq. (44) and confirm the
efficiency of estimators constructed from Eq. (43).
The quantities least accurately estimated are the
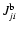 .
Thus, in the above simulation, the mean fractional and absolute fractional
errors of the
.
Thus, in the above simulation, the mean fractional and absolute fractional
errors of the
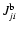 for the Balmer lines in all shells are
for the Balmer lines in all shells are
 and
and
 ,
respectively. In this case,
sampling errors clearly dominate over any systematic bias due to
discretization errors.
This is no suprise since the summation in Eq. (46) includes only those
r-packets that are red-shifted into resonance with the transition
,
respectively. In this case,
sampling errors clearly dominate over any systematic bias due to
discretization errors.
This is no suprise since the summation in Eq. (46) includes only those
r-packets that are red-shifted into resonance with the transition
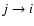 .
Accordingly, even with
.
Accordingly, even with
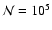 ,
the number
of packets contributing to the summation for a particular
,
the number
of packets contributing to the summation for a particular
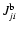 is not large. For example, in the case of the Balmer lines, the
number is
is not large. For example, in the case of the Balmer lines, the
number is  35 at m = 1 rising to
35 at m = 1 rising to  300 at
300 at
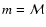 .
.
These relatively large sampling errors for the
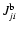 are the main source of error for the coefficients in the
equations of statistical equilibrium.
Of course, for a typical level, there are several source terms, some
not even subject to sampling errors; and so the fractional sampling
error of the total input rate will be correpondingly reduced. Nevertheless,
for a level populated predominately by a single radiative b-b transition,
its niwill directly reflect the sampling error of the relevant
are the main source of error for the coefficients in the
equations of statistical equilibrium.
Of course, for a typical level, there are several source terms, some
not even subject to sampling errors; and so the fractional sampling
error of the total input rate will be correpondingly reduced. Nevertheless,
for a level populated predominately by a single radiative b-b transition,
its niwill directly reflect the sampling error of the relevant
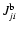 .
But since sampling errors differ from one iteration to
the next, levels suffering this sensitivity will display fluctuating values
of ni and so should not escape notice.
.
But since sampling errors differ from one iteration to
the next, levels suffering this sensitivity will display fluctuating values
of ni and so should not escape notice.
To investigate convergence to the NLTE solution, the values of T and ni throughout the envelope were monitored for 20 outer
iterations in a calculation with
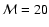 shells and
shells and
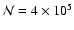 packets. The envelope's parameters are as
specified in Sect. 2.2, and the calculation is initiated as described in
Sect. 3.4. Thus, for the first iteration, the MC transition probabilities
are computed with radiative and collisional rates corresponding to the
initial analytical
model of the radiation field - Eq. (4) - and to the inital guesses for ni and T. For all subsequent iterations,
the MC transition probabilities are computed from the MC radiation field
via the MC estimators of Sect. 6.2, and the ni and T are the
updated values resulting from bringing the matter into statistical and
thermal equilibrium with the MC radiation field.
packets. The envelope's parameters are as
specified in Sect. 2.2, and the calculation is initiated as described in
Sect. 3.4. Thus, for the first iteration, the MC transition probabilities
are computed with radiative and collisional rates corresponding to the
initial analytical
model of the radiation field - Eq. (4) - and to the inital guesses for ni and T. For all subsequent iterations,
the MC transition probabilities are computed from the MC radiation field
via the MC estimators of Sect. 6.2, and the ni and T are the
updated values resulting from bringing the matter into statistical and
thermal equilibrium with the MC radiation field.
Figure 1 shows how the envelope's temperature stratification
evolves from the initial T = 5000 K as the iterations proceed.
The corrections are seen to
be substantial for iterations 1-4 and negligibly
small thereafter. Thus the scheme appears to converge at the fifth iteration,
with the changes introduced at iterations 6-20 presumably being
random fluctuations about the exact NLTE solution. Such fluctuations are
expected because of different sampling errors in successive realisations of
the MC radiation field.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f1.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg280.gif) |
Figure 1:
Convergence of constrained  -iterations. Results of 20
temperature iterations starting from an isothermal stratification with
T = 5000 K are plotted for a simulation with -iterations. Results of 20
temperature iterations starting from an isothermal stratification with
T = 5000 K are plotted for a simulation with
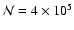 packets. The solution for the conical radiation field is plotted as open
circles. packets. The solution for the conical radiation field is plotted as open
circles. |
To support this claim that the scheme has indeed achieved rapid
convergence
to the close neighbourhood of the exact NLTE solution, a separate
NLTE calculation has been carried out with line formation again treated
in the Sobolev approximation but now with the continuum radiation field
approximated by the free-streaming model described in Sect. 7.1. With the
radiation field thus prescribed, the determination of ni and T at
radius r from the equations of statistical and thermal equilibrium is
a one-point problem. The coefficients in these equations are calculated
with accurate numerical integrations as for the accuracy tests of Sect. 7.1
and then ni and T obtained with the back-substitution iterations of
Sect. 6.4. This one-point calculation has been carried out at several radii,
with the results plotted as open circles in Fig. 1. The agreement with
the MC solutions for iterations 6-20 is excellent.
Given that the scheme has indeed converged and that the remaining
temperature
fluctations are therefore due to sampling errors, the next question is
whether such fluctuations are unacceptably large. Assuming convergence at
iteration 6, we derive an accurate estimate
 of the exact Tfor each shell by averaging over iterations 6-20. The standard deviation
of the fluctuations
of the exact Tfor each shell by averaging over iterations 6-20. The standard deviation
of the fluctuations
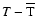 can then be computed for each shell as
well as a consolidated value
can then be computed for each shell as
well as a consolidated value
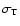 for the entire envelope. For this
simulation with
for the entire envelope. For this
simulation with
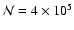 ,
we find that
,
we find that
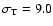 K. Temperature uncertainties of this magnitude are
admittedly large
compared to
the nominal precision - often <0.01 K - achieved by conventional NLTE codes.
But in view of the parametric, geometrical
and kinematic uncertainties associated with specifying the structure of
any celestial object, errors of
K. Temperature uncertainties of this magnitude are
admittedly large
compared to
the nominal precision - often <0.01 K - achieved by conventional NLTE codes.
But in view of the parametric, geometrical
and kinematic uncertainties associated with specifying the structure of
any celestial object, errors of  10 K are completely inconsequential.
10 K are completely inconsequential.
The amplitude of the fluctuations following convergence depend of
course on 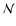 .
Repeating the above simulation with
.
Repeating the above simulation with
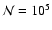 and again averaging over iterations 6-20,
we find that
and again averaging over iterations 6-20,
we find that
 increases to 16.2 K, consistent with the expected
scaling
increases to 16.2 K, consistent with the expected
scaling
 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f2.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg286.gif) |
Figure 2:
Convergence of constrained 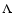 -iterations. Results of 20
level population iterations starting from Saha-Boltzmann populations at
T = 5000 K are plotted for the mass shell m = 10 in a simulation with -iterations. Results of 20
level population iterations starting from Saha-Boltzmann populations at
T = 5000 K are plotted for the mass shell m = 10 in a simulation with
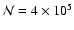 packets. The solution for the conical radiation field is plotted as open
circles. packets. The solution for the conical radiation field is plotted as open
circles. |
The convergence behaviour of the ni for the same 20 iterations
of the above model with
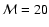 shells and
shells and
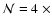 105 packets is shown in Fig. 2 for shell m = 10.
Again we see substantial corrections in the first few iterations followed
by fluctations of moderate amplitude about the scheme's solution in the
limit
105 packets is shown in Fig. 2 for shell m = 10.
Again we see substantial corrections in the first few iterations followed
by fluctations of moderate amplitude about the scheme's solution in the
limit
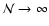 .
.
As for the temperature iterations, the MC solution is compared to
the accurate NLTE solution for the conical radiation field of Sect. 7.1.
The agreement is excellent for low levels and for the continuum (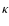 )
but small discrepancies are evident for high levels. This probably reflects
a small difference in the two calculations due to the device used in the
MC calculation to avoid negative probabilities when
)
but small discrepancies are evident for high levels. This probably reflects
a small difference in the two calculations due to the device used in the
MC calculation to avoid negative probabilities when
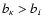 - see Sect. 4.3.1.
- see Sect. 4.3.1.
A further test of the accuracy of the converged ni is presented
in Fig. 3. In this diagram, the variation with radius of the departure
coefficients for several levels are compared to the corresponding values
for the conical radiation field. The agreement is seen to be satisfactory.
The behaviour of the H level populations in this SN envelope are
qualitatively similar to those of the hydrogenic ion He+ in W-R winds
(Hillier 1987). In particular, photoionizations predominantly occur from
level 2, which
behaves like a ground state, becoming overpopulated in the outer layers due
to the dilution of the ionizing continuum shortward of 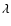 3646 Å and to the trapping of Lyman
3646 Å and to the trapping of Lyman 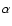 photons.
photons.
Note that, because most H atoms are in the ground state for both the
NLTE and the LTE solutions, the departure coefficient b1 is almost
exactly = 1. Accordingly, the values b2 plotted in Fig. 3 directly
indicate the decoupling of level n = 2 from the ground state.
Given that the macro-atom formalism has now been extended to include
interactions with the thermal pool, it is of interest to test this extension
by repeating the consistency test of level emissivities described for H
in Sect. 5.2 of Paper I.
When the outer iterations have converged, the level populations,
temperature and radiative rates appropriate to statistical and
thermal equilibrium are known for each mass shell. From this
information, the rates at which radiant energy is being converted to other
forms can be computed for each of the processes operating. Specifically,
these are: conversions into excitation energy by b-b absorptions to levels
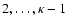 ;
conversion into ionization energy by b-f absorptions;
and conversions into thermal energy by b-f and f-f absorptions. These last
two processes, labelled
;
conversion into ionization energy by b-f absorptions;
and conversions into thermal energy by b-f and f-f absorptions. These last
two processes, labelled 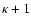 and
and 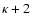 ,
were not included in
Paper I, which treated only statistical equilibrium.
,
were not included in
Paper I, which treated only statistical equilibrium.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f3.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg292.gif) |
Figure 3:
Test of departure coefficients bi. Results obtained at
iteration 20 in Monte Carlo calculation with
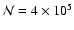 packets are plotted as solid lines for the indicated levels.
The solutions for the conical radiation field are plotted as filled circles (i=2), open circles (i=3) and asterisks (i=10). packets are plotted as solid lines for the indicated levels.
The solutions for the conical radiation field are plotted as filled circles (i=2), open circles (i=3) and asterisks (i=10). |
From these conversion rates, a Monte Carlo test of the MC transition
probabilities is carried out for each mass shell as follows:
N = 106equal energy r-packets are assigned to these absorption
channels in
proportion to the computed conversion rates. Those assigned to processes
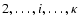 activate a macro-atom to state i, while
those assigned to processes
activate a macro-atom to state i, while
those assigned to processes 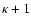 and
and 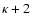 result in the creation
of a k-packet. Application of the MC transition probabilities then
results eventually in the emission of an r-packet as described in Sect. 4.
Moreover, each emitted r-packet belongs to one of the
result in the creation
of a k-packet. Application of the MC transition probabilities then
results eventually in the emission of an r-packet as described in Sect. 4.
Moreover, each emitted r-packet belongs to one of the
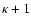 emission processes representing the inverse of the above absorption
processes. Accordingly, when all N packets have been absorbed and
re-emitted, we have experimental values Ni for each of the
emission processes representing the inverse of the above absorption
processes. Accordingly, when all N packets have been absorbed and
re-emitted, we have experimental values Ni for each of the
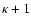 emission processes.
emission processes.
But the rates at which excitation, ionization and thermal energy
is being converted in a given shell into radiant energy can be directly
computed from the
known level populations and temperature - i.e., from the rates of the
various b-b, f-b and f-f processes. Thus, we can predict that N*i of the N packets should have been emitted by process i.
In Paper I, Fig. 4, the agreement of Ni and N*i was
shown graphically. Here, more rigorously, we compute the values of
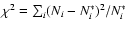 for each mass shell.
Since there are 16 emission channels, we expect the experimental values of
for each mass shell.
Since there are 16 emission channels, we expect the experimental values of 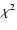 to be distributed as
to be distributed as
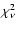 with
with 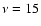 degrees of
freedom. Thus, 50 percent of the values should be <14.34 and
95 percent <25.00
degrees of
freedom. Thus, 50 percent of the values should be <14.34 and
95 percent <25.00
The results obtained after the 20th iteration for the model with
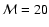 discussed in
Sect. 7.2 are as follows: the 20 values of
discussed in
Sect. 7.2 are as follows: the 20 values of 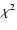 range from 7.87 to 34.22, with 6 < 14.34 and 3 > 25.00.
range from 7.87 to 34.22, with 6 < 14.34 and 3 > 25.00.
The outcome of this test is that the experimental values of 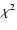 are slightly biased to higher values than predicted by the
are slightly biased to higher values than predicted by the
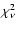 distribution. However, given that the underlying model
has departures from strict statistical and thermal equilibrium because
of its own MC sampling errors, these results are in fact a strong
confirmation that
the extension of the macro-atom formalism to include interactions with the
thermal pool has been carried out correctly.
distribution. However, given that the underlying model
has departures from strict statistical and thermal equilibrium because
of its own MC sampling errors, these results are in fact a strong
confirmation that
the extension of the macro-atom formalism to include interactions with the
thermal pool has been carried out correctly.
As a further test of this conclusion, values of 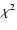 were
computed with the summation restricted to the three channels containing
r-packets emitted by f-b and f-f processes. In this case, the values for
all shells are <7.81, the 95 percent confidence limit for
were
computed with the summation restricted to the three channels containing
r-packets emitted by f-b and f-f processes. In this case, the values for
all shells are <7.81, the 95 percent confidence limit for 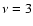 degrees of freedom. This eliminates the possibility that the above upward
bias is due to poor predictions for the continuum channels.
degrees of freedom. This eliminates the possibility that the above upward
bias is due to poor predictions for the continuum channels.
When the outer iteration loop has converged, the r-packets that
escaped to 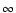 during the last iteration provide a crude estimate of the
SN's emergent spectrum. This is obtained by simply allocating each escaping
packet's rest energy
during the last iteration provide a crude estimate of the
SN's emergent spectrum. This is obtained by simply allocating each escaping
packet's rest energy
 to its appropriate bin in a grid of rest
frequencies. This crude spectrum is shown in Fig. 4 for the above model with
to its appropriate bin in a grid of rest
frequencies. This crude spectrum is shown in Fig. 4 for the above model with
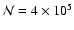 packets. In this figure, luminosity density is
plotted against vacuum wavelength in the optical domain and, despite sampling
errors, the P Cygni line profiles of H
packets. In this figure, luminosity density is
plotted against vacuum wavelength in the optical domain and, despite sampling
errors, the P Cygni line profiles of H and H
and H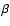 are clearly
seen.
are clearly
seen.
If this MC code were intended for use in interpreting observational
data, the crude MC spectrum shown in Fig. 4 would not be compared with the
observed spectrum. Instead, a far less noisy theoretical spectrum would be
computed by following a procedure described earlier (Lucy 1999b).
Specifically, estimates of line- and continuum source functions can be
derived from the same
MC simulation and used to compute a high quality spectrum from the
formal integral for the emergent intensity as a function of impact parameter.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f4.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg299.gif) |
Figure 4:
Monte Carlo spectrum obtained at
iteration 20 in Monte Carlo calculation with
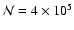 packets. The unit of luminosity density is 1045 erg s-1 cm-1.
The rest wavelengths of H packets. The unit of luminosity density is 1045 erg s-1 cm-1.
The rest wavelengths of H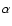 ,
H ,
H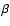 and H
and H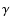 are indicated.
are indicated. |
In Paper I, the radiative and collisional interactions of an atomic species
in statistical equilibrium with its environment was modelled in terms of
macro-atoms being activated and de-activated by the absorption and emission
of e-packets. In this paper, this macroscopic quantization
has been extended to include interactions with the thermal pool
on the assumption of local thermal balance - i.e.,
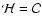 .
(But note that departures from thermal equilibrium due to non-radiative
heating can be incorporated as described in Sect. 7.2 of Paper I.)
.
(But note that departures from thermal equilibrium due to non-radiative
heating can be incorporated as described in Sect. 7.2 of Paper I.)
With this extension, the macro-atom formalism allows
MC transfer codes to obtain NLTE solutions for stratified atmospheres. As a
first test of this, this paper describes a MC code treating the formation
of the H spectrum in a type II SN, with the emphasis being on demonstrating
the consistency of the technique as
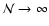 ,
the
accuracy of the estimators of the various radiative rates for feasible
values of
,
the
accuracy of the estimators of the various radiative rates for feasible
values of  ,
and the convergence behaviour of the constrained
,
and the convergence behaviour of the constrained
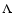 -iteration scheme.
-iteration scheme.
Given that consistency has been demonstrated and that the
geometry-independent  -iteration scheme converges, applications
to problems with arbitrary geometry and to multiple-species plasmas are
now in principle possible. But considering the detail and resolution required
to have impact on a current research topic, such problems will undoubtedly
require a substantial increase in computational resources over those
deployed here
for a 1D envelope of pure H. Even with the efficient estimators
of Sect. 6.2, each cell in the numerical grid must still be traversed by
numerous r-packets if adequate accuracy is to be achieved. This requirement
obviously mandates a huge increase in
-iteration scheme converges, applications
to problems with arbitrary geometry and to multiple-species plasmas are
now in principle possible. But considering the detail and resolution required
to have impact on a current research topic, such problems will undoubtedly
require a substantial increase in computational resources over those
deployed here
for a 1D envelope of pure H. Even with the efficient estimators
of Sect. 6.2, each cell in the numerical grid must still be traversed by
numerous r-packets if adequate accuracy is to be achieved. This requirement
obviously mandates a huge increase in 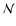 for 2- and 3D problems.
But also in 1D problems for static atmospheres, narrow line widths
will demand large values of
for 2- and 3D problems.
But also in 1D problems for static atmospheres, narrow line widths
will demand large values of 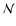 in order to get accurate b-b transition rates.
in order to get accurate b-b transition rates.
A further problem arises if the lower boundary of the
computational domain is at a large optical depth in the continuum. Each
r-packet's interaction history will then comprise numerous events and will
often end with a recrossing of the lower boundary, thus reducing the
number of r-packets traversing the cells in the outer atmosphere.
This requirement for substantial computer resources suggests the
use of a computer with numerous parallel processors. Fortunately,
this MC technique is extremely well suited for such machines, especially those
with large shared memory. A MC transfer calculation can then be equally
divided between the processors, each of which carries its task to
completion with no exchanges of information or packets with other processors.
Following completion, the individual processors'
contributions to the estimator summations are added to obtain the
radiative rates for all cells, which are then equally divided among the
processors to solve the equations of statistical and thermal equilibrium.
These remarks suggest that close to the maximum theoretical efficiency
should be achievable.
The long-term aim in devoloping the macro-atom formalism is
to obtain accurate NLTE solutions for multi-dimensional problems using MC methods. But the technique is likely to be of more immediate use
in obtaining approximate NLTE solutions with precision sufficient
for current research problems. The reasons for optimism in this regard are
that, even without the converged stratifications of temperature and level
populations, the technique rigorously obeys radiative equilibrium and also
provides remarkably accurate emissivites (Paper I, Sect. 6). Thus, for some
problems, adequate accuracy will be achieved by using analytic ionization
and excitation formulae, as in previous stellar wind and SNe codes, but then
computing the radiation field with this MC technique replacing the earlier
techniques that assumed coherent scattering (Abbott & Lucy 1985) or downward
branching (Lucy 1999b). For yet higher accuracy, ionization could be
solved for while retaining an analytic excitation formula. Compared to the
full NLTE problem, this greatly reduces the demand for large  since
estimates of b-b rates are no longer required. Moreover, for each atomic
species, the statistical equilibrium
equations for perhaps thousands of levels are replaced by the ionization
equations for just
since
estimates of b-b rates are no longer required. Moreover, for each atomic
species, the statistical equilibrium
equations for perhaps thousands of levels are replaced by the ionization
equations for just 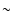 3-5 ions.
Despite this enormous simplification, the anticipated loss of accuracy is
slight in view of the afore-mentioned accurate MC emissivities.
3-5 ions.
Despite this enormous simplification, the anticipated loss of accuracy is
slight in view of the afore-mentioned accurate MC emissivities.
Acknowledgements
I am grateful to S.Sim for a discussion on the potential application of
parallel processors.
-
Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679
NASA ADS
-
Arnett, W. D. 1988, ApJ, 331, 377
NASA ADS
-
Castor, J. I. 1970, MNRAS, 149, 111
NASA ADS
-
Duschinger, M., Puls, J., Branch, D., Hoeflich, P., & Gabler, A. 1995, A&A, 297,
802
NASA ADS
-
Hillier, D. J. 1987, ApJS, 63, 947
NASA ADS
-
Lucy, L. B. 1971, ApJ, 163, 95
NASA ADS
-
Lucy, L. B. 1987, in ESO Workshop on SN 1987A, ed. I. J. Danziger, 417
-
Lucy, L. B. 1999a, A&A, 344, 282
NASA ADS
-
Lucy, L. B. 1999b, A&A, 345, 211
NASA ADS
-
Lucy, L. B. 2002, A&A, 384, 725
NASA ADS
-
Mazzali, P. A., & Lucy, L. B. 1993, A&A, 279, 447
NASA ADS
-
McCrea, W. H., & Mitra, K. K. 1936, Zs.f.Ap., 11, 359
-
Mihalas, D. 1978, Stellar Atmospheres 2nd ed. (San Francisco: W. H. Freeman & Co.)
-
Osterbrock; D. E. 1974, Astrophysics of Gaseous Nebulae (San Francisco: W. H. Freeman & Co.)
-
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical
Recipes (Cambridge: Cambridge Univ. Press)
-
Suntzeff, N. B., & Bouchet, P. 1990, AJ, 99, 650
NASA ADS
-
van Regemorter, H. 1962, ApJ, 136, 906
NASA ADS
Copyright ESO 2003
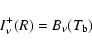
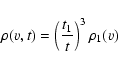
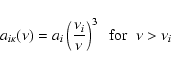
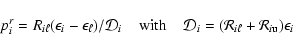
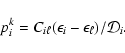
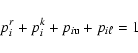
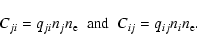
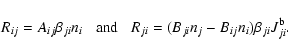
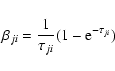
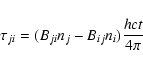
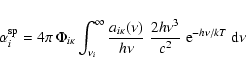
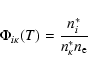
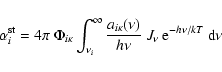
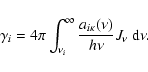
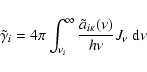
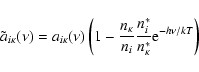
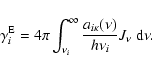
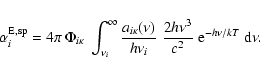
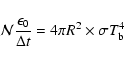
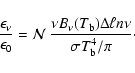
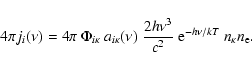
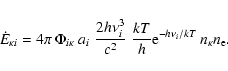
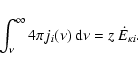
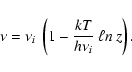
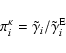
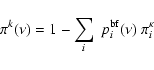
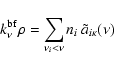
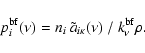
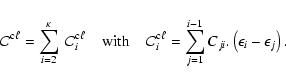
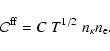
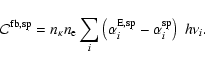
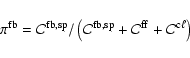
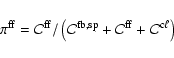
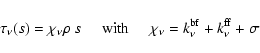
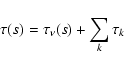
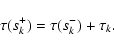
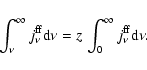
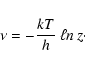
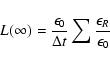
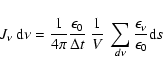
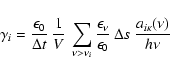
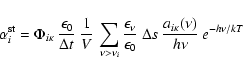
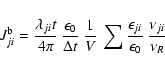
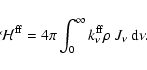
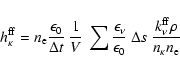
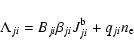
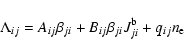
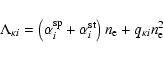
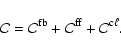
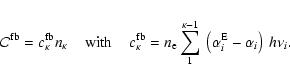
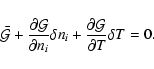
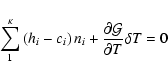
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f1.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg280.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f2.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg286.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f3.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg292.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3550.f4.ps}
\end{figure}](/articles/aa/full/2003/19/aa3550/Timg299.gif)