A&A 403, 303-312 (2003)
DOI: 10.1051/0004-6361:20030356
Numerical constraints on the model of stochastic excitation
of solar-type oscillations
R. Samadi 1,2 -
Å. Nordlund 3 - R. F. Stein 4
- M. J. Goupil 2 - I. Roxburgh 1,2
1 - Astronomy Unit, Queen Mary, University of London, London E14NS, UK
2 -
Observatoire de Paris, LESIA, CNRS UMR 8109, 92195 Meudon, France
3 -
Niels Bohr Institute for Astronomy Physics and Geophysics, Copenhagen, Denmark
4 -
Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan, USA
Received 7 November 2002 / Accepted 7 March 2003
Abstract
Analyses of a 3D simulation of the upper layers of
a solar convective envelope provide
constraints on the physical quantities
which enter the theoretical formulation of a stochastic excitation model
of solar p modes, for instance the convective velocities
and the turbulent kinetic energy spectrum.
These constraints are then used to compute the acoustic excitation rate
for solar p modes, P.
The resulting values are found  5 times larger
than the values resulting from a computation in which
convective velocities and entropy fluctuations are obtained with a 1D solar envelope model
built with the time-dependent, nonlocal Gough (1977) extension
of the mixing length formulation for convection (GMLT).
5 times larger
than the values resulting from a computation in which
convective velocities and entropy fluctuations are obtained with a 1D solar envelope model
built with the time-dependent, nonlocal Gough (1977) extension
of the mixing length formulation for convection (GMLT).
This difference is mainly due to the assumed mean
anisotropy properties of the velocity field in the excitation region. The 3D
simulation suggests much larger horizontal velocities compared to vertical
ones than in the 1D GMLT solar model.
The values of P obtained with the 3D simulation constraints
however are still too small compared
with the values inferred from solar observations.
Improvements in the description of the turbulent kinetic energy
spectrum and its depth dependence
yield further increased theoretical values of P which bring them closer
to the observations. It is also found that the source of excitation
arising from the advection of the turbulent fluctuations of entropy
by the turbulent movements contributes 
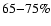 to the excitation
and therefore remains
dominant over the Reynolds stress contribution.
The derived theoretical values of P
obtained with the 3D simulation constraints
remain smaller by a factor
to the excitation
and therefore remains
dominant over the Reynolds stress contribution.
The derived theoretical values of P
obtained with the 3D simulation constraints
remain smaller by a factor  3
compared with the solar observations. This shows that
the stochastic excitation model still needs to be improved.
3
compared with the solar observations. This shows that
the stochastic excitation model still needs to be improved.
Key words: convection - turbulence - stars: oscillations - Sun: oscillations
Solar-type oscillations are believed to be stochastically excited by turbulent
convection in the near-surface layers of the star.
The excitation is caused by turbulent convective motions
which generate acoustic energy which in turn is injected into the p modes
(e.g. Goldreich & Keeley 1977).
Measurements of the acoustic energy injected into solar-like
oscillations are among the goals of future space seismic missions such
as the COROT (Baglin & The Corot Team 1998) and Eddington (Favata et al. 2000) missions.
These seismic data will make it possible to constrain the theory of the
oscillation excitation and damping, to provide valuable information
about the properties of stellar convection, and hence
to severely constrain stellar models.
Models for stochastic excitation of stellar p modes have been
proposed by several authors, (e.g. Goldreich & Keeley 1977; Osaki 1990; Balmforth 1992a; Goldreich et al. 1994; Samadi & Goupil 2001).
These theoretical approaches
yield the acoustic energy injected into solar-like
oscillations.
This offers the advantage of
testing separately several properties entering the excitation mechanism
which are not well understood or modeled.
Such approaches require simplifying assumptions
which need to be validated before they can be used with confidence.
They require an accurate knowledge of the properties of turbulent convection and,
unfortunately, current observations of the
solar granulation cannot provide a
determination of the turbulent spectrum precise enough in the present context
(Rieutord et al. 2000; Nordlund et al. 1997).
On the theoretical side, theoretical models of turbulent convection, such as the mixing-length approaches or multiple size eddies approaches (e.g. Canuto & Mazzitelli 1991; Canuto et al. 1996), provide a too limited description of
the characteristic scale length of the solar turbulent spectrum.
These theoretical formulations of stochastic excitation also involve
scaling parameters which are determined to by the requirement that
the computed values of the oscillation
amplitudes give the best fit to the solar seismic measurements (e.g. Houdek et al. 1999; Samadi et al. 2001, Paper II hereafter).
When the scaling parameters are
so adjusted, constraints and
validation on the turbulent stellar medium
can only come from seismic observations of other stars.
Such accurate data on the excitation rates
for other stars than the Sun are not yet available.
An alternative way is then to consider
results from 3D numerical simulations. They indeed
enable one to compute directly the rate at which p modes
are excited (e.g. this was undertaken for the Sun by Stein & Nordlund 2001).
Such methods are time consuming and do not easily allow
massive computations of the excitation rate for stars
with different temperatures and luminosities.
They can provide quantities which can be implemented
in a formulation for the excitation rate P.
In any case we cannot avoid to use a 1D model for computing accurate
eigenfrequencies for the whole observed frequency range.
The purpose of the present paper is to provide
a better insight into the excitation model
with a semianalytical approach but
using a model of turbulence and values of
the scaling parameters
derived from a 3D simulation of the solar outer layers.
We consider in this work the theoretical formulation of stochastic excitation
by Samadi & Goupil (2001, hereafter Paper I, see also Samadi 2001 for a detailed summary) which includes a detailed treatment of turbulent convection.
This formulation involves two scaling parameters
which are related to the spatial and temporal
characteristics of the turbulence model.
Our final goal is to test the excitation model without adjusting these parameters
and without the use of the mixing-length approach for estimating convective
velocities and entropy fluctuations.
The paper is organized as follows: in Sect. 2
we briefly recall
the adopted formulation for estimating the rate at which
turbulent convection supplies energy to the p modes (excitation rate 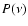 ).
We emphasize some assumptions and approximations
entering this formulation.
).
We emphasize some assumptions and approximations
entering this formulation.
In Sect. 3,
a 3D numerical simulation of the upper part of the solar convection zone
is used in order to determine the time averaged
properties of turbulent convection: this provides
constraints on the ingredients involved in the
theoretical expression of the excitation rate,
such as scaling parameters, velocity anisotropy factor,
the values of convective velocities and entropy fluctuations
and the k (wavenumber) dependence of the kinetic turbulent spectrum.
These constraints are then used in Sect. 4
to compute the excitation rate 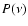 ,
for radial solar p modes.
The results are compared with solar seismic observations as given
in Chaplin et al. (1998) and with a 1D mixing-length model built according
to Gough (1977)'s non-local formulation of the mixing-length theory
(GMLT hereafter).
In Sect. 5 we summarize our results and
discuss some possible origins of the remaining discrepancies
with solar seismic observations and results by Stein & Nordlund (2001).
,
for radial solar p modes.
The results are compared with solar seismic observations as given
in Chaplin et al. (1998) and with a 1D mixing-length model built according
to Gough (1977)'s non-local formulation of the mixing-length theory
(GMLT hereafter).
In Sect. 5 we summarize our results and
discuss some possible origins of the remaining discrepancies
with solar seismic observations and results by Stein & Nordlund (2001).
2 Stochastic excitation
The rate at which turbulent motions of the convective elements supply
energy to acoustic oscillation modes is computed as in
Paper I. For a given mode with eigenfrequency 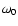 ,
the excitation rate
can be written as (Eqs. (58) and (59) of Paper I):
,
the excitation rate
can be written as (Eqs. (58) and (59) of Paper I):
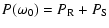 |
|
|
(1) |
where
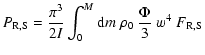 |
|
|
(2) |
where 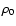 is the mean averaged density,
w is the rms value of the vertical component of the velocity,
is the mean averaged density,
w is the rms value of the vertical component of the velocity,
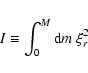 |
(3) |
is the mode inertia,
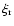 is the
radial component of the fluid displacement adiabatic eigenfunction
is the
radial component of the fluid displacement adiabatic eigenfunction 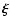 ,
and
,
and  is an anisotropy factor.
Following Gough (1977), we define
is an anisotropy factor.
Following Gough (1977), we define
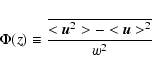 |
(4) |
where 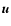 is the velocity field, < . > denotes horizontal average and
is the velocity field, < . > denotes horizontal average and
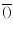 denotes time average.
The mean vertical velocity, w, is defined as:
denotes time average.
The mean vertical velocity, w, is defined as:
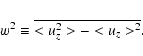 |
(5) |
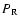 ,
,
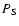 respectively account
for the excitation by the Reynolds stress and for the
excitation resulting from the advection of the entropy fluctuations
by the turbulent velocity field (the so-called entropy source term).
Here the entropy term (
respectively account
for the excitation by the Reynolds stress and for the
excitation resulting from the advection of the entropy fluctuations
by the turbulent velocity field (the so-called entropy source term).
Here the entropy term (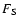 )
is an advective term
which mixes turbulent pressure and entropy fluctuations.
Expressions for
)
is an advective term
which mixes turbulent pressure and entropy fluctuations.
Expressions for 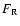 ,
,
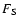 are:
are:
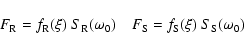 |
(6) |
with
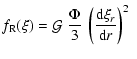 |
|
|
(7) |
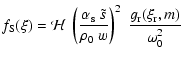 |
|
|
(8) |
where
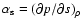 ,
p denotes the pressure and s the entropy,
,
p denotes the pressure and s the entropy,
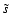 is the rms value of the entropy fluctuations, and
is the rms value of the entropy fluctuations, and
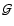 and
and 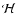 are anisotropy factors.
We assume that injection of acoustic energy
into the modes is isotropic. This assumption
implies
are anisotropy factors.
We assume that injection of acoustic energy
into the modes is isotropic. This assumption
implies
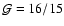 and
and
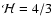 in
Eqs. (7) and (8) above.
Effects of the space averaged anisotropy
in the driving process is investigated
in Sect. 4.1.2.
in
Eqs. (7) and (8) above.
Effects of the space averaged anisotropy
in the driving process is investigated
in Sect. 4.1.2.
The function
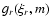 is defined as:
is defined as:
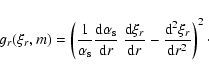 |
(9) |
One can show that the Reynolds contribution - 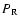 - scales
as
- scales
as
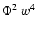 while the source term involving
the entropy fluctuations -
while the source term involving
the entropy fluctuations - 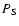 - scales as
- scales as
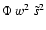 .
.
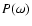 is thus very dependent of the estimated values
of w2,
is thus very dependent of the estimated values
of w2,
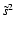 and
and  .
The MLT provides estimates for w but
.
The MLT provides estimates for w but  is a free parameter.
For isotropic turbulence
is a free parameter.
For isotropic turbulence 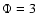 ,
and in Böhm-Vitense (1958, BV-MLT hereafter)
formulation
,
and in Böhm-Vitense (1958, BV-MLT hereafter)
formulation 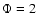 .
In the present paper, unless otherwise stated,
.
In the present paper, unless otherwise stated,
 is given by a simulation of the upper part of the solar
convective zone in Sect. 3.4 below.
is given by a simulation of the upper part of the solar
convective zone in Sect. 3.4 below.
For the driving sources in Eq. (6):
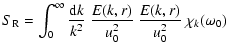 |
|
|
(10) |
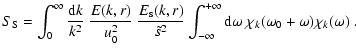 |
|
|
(11) |
E(k) represents the kinetic energy spectrum associated with the
turbulent velocity field and
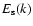 models the spectrum of
the turbulent entropy fluctuations, with k the eddy wavenumber.
The time-dependent part of the turbulent spectrum is described by the
function
models the spectrum of
the turbulent entropy fluctuations, with k the eddy wavenumber.
The time-dependent part of the turbulent spectrum is described by the
function
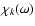 which models the correlation time-scale of an
eddy with wavenumber k.
The quantity
which models the correlation time-scale of an
eddy with wavenumber k.
The quantity
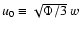 is introduced for convenience (see Eq. (17)),
is introduced for convenience (see Eq. (17)),
The above expression for P is mainly based on the assumption that the medium is
incompressible. In other words,
we adopt the Boussinesq approximation i.e.
assume a homogeneous model for
the turbulence and the excitation mechanism.
We therefore neglect effects of the stratification in the excitation process.
2.2 The turbulence model
Let k0(r) be the wavenumber at which energy
is injected into the turbulent cascade and the energy E(k) is maximum.
k0(r) is related to the mixing-length
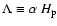 by (Paper I):
by (Paper I):
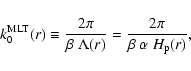 |
(12) |
where 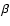 is a parameter of order unity,
is a parameter of order unity, 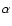 is the mixing-length
parameter and
is the mixing-length
parameter and 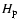 is the pressure scale-height.
This is a natural way to estimate k0 as
is the pressure scale-height.
This is a natural way to estimate k0 as 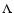 is the characteristic length of the largest convective elements.
is the characteristic length of the largest convective elements.
The Gaussian function is usually assumed for modeling
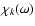 (e.g. Stein 1967; Goldreich & Keeley 1977)
as a consequence of the turbulent nature of the
medium where the stochastic excitation occurs.
The Gaussian function takes the form
(e.g. Stein 1967; Goldreich & Keeley 1977)
as a consequence of the turbulent nature of the
medium where the stochastic excitation occurs.
The Gaussian function takes the form
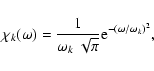 |
(13) |
where 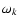 is its linewidth.
is its linewidth.
Let 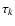 be the characteristic time correlation length of an eddy of wavenumber k.
Equation (13) corresponds in the time domain to a Gaussian function
with linewidth equal to
be the characteristic time correlation length of an eddy of wavenumber k.
Equation (13) corresponds in the time domain to a Gaussian function
with linewidth equal to
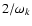 .
Then
.
Then
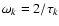 for a Gaussian time spectrum.
for a Gaussian time spectrum.
The energy supply rate P crucially depends on the correlation time-scale
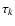 (see Paper II). Following Balmforth (1992a) we define it as:
(see Paper II). Following Balmforth (1992a) we define it as:
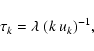 |
(14) |
where uk is the velocity of an eddy with wavenumber k.
The velocity uk is obtained from the kinetic energy spectrum E(k)
(Stein 1967)
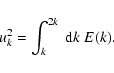 |
(15) |
E(k) is normalised such that:
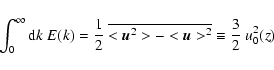 |
(16) |
where u0 is introduced for convenience.
According to Eqs. (4) and (16),
u0 and w are then related to each other by
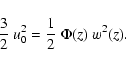 |
(17) |
The parameter 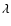 in Eq. (14)
accounts for our lack of precise knowledge of the
time correlation
in Eq. (14)
accounts for our lack of precise knowledge of the
time correlation 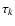 in stellar conditions.
In the present paper, we assume
in stellar conditions.
In the present paper, we assume  while
while 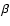 (Eq. (12))
and
(Eq. (12))
and 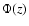 (Eq. (4)) are given by a simulation of the upper part of the solar convective zone
in Sect. 3.4 below.
(Eq. (4)) are given by a simulation of the upper part of the solar convective zone
in Sect. 3.4 below.
In practice, we compute the excitation rate 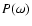 according to Eq. (1). The calculation requires the knowledge of
several quantities which can be obtained either from a 1D model (Paper II)
or at least partly from a 3D simulation.
Comparison of the results using both options yields insights in the excitation
mechanism and its modelling. Hence in the following:
according to Eq. (1). The calculation requires the knowledge of
several quantities which can be obtained either from a 1D model (Paper II)
or at least partly from a 3D simulation.
Comparison of the results using both options yields insights in the excitation
mechanism and its modelling. Hence in the following:
 The velocity, entropy fluctuations, anisotropy and turbulent spectra
E's are obtained from a 3D
simulation as described in the next section.
The velocity, entropy fluctuations, anisotropy and turbulent spectra
E's are obtained from a 3D
simulation as described in the next section.
 The mean density,
The mean density, 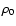 ,
the thermodynamic quantity
,
the thermodynamic quantity
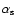 ,
the oscillation properties - eigenfrequencies
and eigenfunctions - are calculated from a
solar envelope equilibrium model and Balmforth (1992b)'s pulsation code.
The envelope model is built with a treatment of convection as prescribed
by the GMLT formulation and
is computed in the manner of
Balmforth (1992b) and Houdek et al. (1999). This solar envelope model
(hereafter GMLT solar model) is identical to the one
considered in Samadi et al. (2002, hereafter Paper III). In particular, it incorporates
turbulent pressure (momentum flux) in the equilibrium model envelope.
The entire envelope is integrated using the equations appropriate to
the nonlocal mixing-length formulation by Gough (1976) and to the Eddington
approximation to radiative transfer (Unno & Spiegel 1966).
The equation of state included a detailed treatment of the ionization of C, N, and O, and a treatment of the ionization of the next seven most abundant elements (Christensen-Dalsgaard 1982), as well as "pressure ionization'' by the method of Eggleton, Faulkner & Flannery (Eggleton et al. 1973).
In this generalization of the mixing-length approach, two additional
parameters, namely a and b, are introduced which control
the spatial coherence of the ensemble of eddies contributing
to the total heat and momentum fluxes (a), and the
degree to which the turbulent fluxes are coupled to the local
stratification (b).
These convection parameters are calibrated to a solar model to obtain the
helioseismically inferred depth of the solar convection zone of 0.287 of
the solar radius (Christensen-Dalsgaard et al. 1991).
The adopted value for the shape factor
,
the oscillation properties - eigenfrequencies
and eigenfunctions - are calculated from a
solar envelope equilibrium model and Balmforth (1992b)'s pulsation code.
The envelope model is built with a treatment of convection as prescribed
by the GMLT formulation and
is computed in the manner of
Balmforth (1992b) and Houdek et al. (1999). This solar envelope model
(hereafter GMLT solar model) is identical to the one
considered in Samadi et al. (2002, hereafter Paper III). In particular, it incorporates
turbulent pressure (momentum flux) in the equilibrium model envelope.
The entire envelope is integrated using the equations appropriate to
the nonlocal mixing-length formulation by Gough (1976) and to the Eddington
approximation to radiative transfer (Unno & Spiegel 1966).
The equation of state included a detailed treatment of the ionization of C, N, and O, and a treatment of the ionization of the next seven most abundant elements (Christensen-Dalsgaard 1982), as well as "pressure ionization'' by the method of Eggleton, Faulkner & Flannery (Eggleton et al. 1973).
In this generalization of the mixing-length approach, two additional
parameters, namely a and b, are introduced which control
the spatial coherence of the ensemble of eddies contributing
to the total heat and momentum fluxes (a), and the
degree to which the turbulent fluxes are coupled to the local
stratification (b).
These convection parameters are calibrated to a solar model to obtain the
helioseismically inferred depth of the solar convection zone of 0.287 of
the solar radius (Christensen-Dalsgaard et al. 1991).
The adopted value for the shape factor
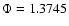 ,
a value which provides the best fit between computed solar damping rates
and measurements by Chaplin et al. (1998) (see Houdek et al. 2001).
The detailed equations describing the equilibrium and pulsation models were
discussed by Balmforth (1992b) and by Houdek (1996).
,
a value which provides the best fit between computed solar damping rates
and measurements by Chaplin et al. (1998) (see Houdek et al. 2001).
The detailed equations describing the equilibrium and pulsation models were
discussed by Balmforth (1992b) and by Houdek (1996).
For implementation in Eqs. (1)-(11),
the quantities from the 3D simulation are interpolated at
the GMLT model mesh points. The grid of
mesh points of the simulated domain is matched
with the GMLT one such
that w in the 3D simulation
has its maximum at the same layer as in the GMLT model.
In the simulation, w peaks  40 km above
the layer at which the mean optical depth
40 km above
the layer at which the mean optical depth 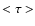 is unity while in the GMLT model,
w peaks
is unity while in the GMLT model,
w peaks  130 km below the photosphere (
130 km below the photosphere (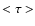 = 2/3).
= 2/3).
3 Constraints from the 3D simulation
We consider a 3D simulation of the upper part of
the solar convective zone obtained with the 3D
numerical code developed at the Niels Bohr Institute for Astronomy,
Physics and Geophysics (Copenhagen, Denmark).
The simulated domain is 3.2 Mm deep and its
surface is 6 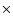 6
6
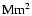 .
The grid of
mesh points is 256
.
The grid of
mesh points is 256 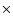 256
256 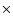 163, the total duration 27 min
and the sampling time 30 s. Physical assumptions are described in Stein & Nordlund (1998).
163, the total duration 27 min
and the sampling time 30 s. Physical assumptions are described in Stein & Nordlund (1998).
Output of the simulation considered here are
the velocity field
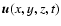 and the entropy
s(x,y,z,t).
They are used to determine the quantities
and the entropy
s(x,y,z,t).
They are used to determine the quantities
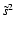 ,
,
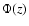 ,
w(z),
,
w(z),
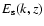 ,
E(k,z)which enter the excitation rate through Eqs. (2), (7), (8), (10), (11).
,
E(k,z)which enter the excitation rate through Eqs. (2), (7), (8), (10), (11).
3.1 Fourier transforms and averaging
We compute the 2D Fourier transform, along horizontal planes,
of the velocity field 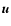 and the entropy s,
at each layer z. This provides
and the entropy s,
at each layer z. This provides
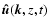 and
and
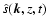 where
where 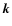 is the
wavenumber along the horizontal plane.
Next we integrate
is the
wavenumber along the horizontal plane.
Next we integrate
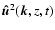 and
and
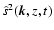 over circles
with radius k at each given layer z.
Finally take a time average of the various
quantities over the time series.
This yields
over circles
with radius k at each given layer z.
Finally take a time average of the various
quantities over the time series.
This yields
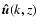 and
and
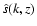 where
where
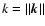 is the wavenumber norm.
is the wavenumber norm.
We define the time averaged kinetic energy spectrum E(k,z) as:
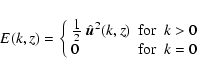 |
(18) |
and the time averaged spectrum of the entropy
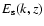 as:
as:
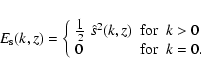 |
(19) |
From Parseval-Plancherel's relation, E(k,z) and
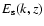 satisfy:
satisfy:
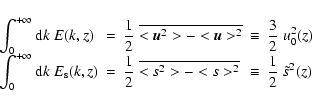 |
(20) |
Hence the definitions of the energy spectra here involve zero mean velocity
and entropy fluctuations.
3.2 Convective velocities and entropy fluctuations
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f1.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg97.gif) |
Figure 1:
The root mean square
of the vertical component of the velocity
(
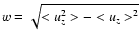 )
in the upper layers of a solar model
is plotted versus depth for the 3D simulation
(solid line) and for the 1D GMLT model
(dashed line). The abscissa is the depth )
in the upper layers of a solar model
is plotted versus depth for the 3D simulation
(solid line) and for the 1D GMLT model
(dashed line). The abscissa is the depth
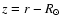 where
where 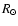 is the radius at the photosphere.
The w maximum corresponds to the top of
the superadiabatic region and is reached at the
depth
is the radius at the photosphere.
The w maximum corresponds to the top of
the superadiabatic region and is reached at the
depth
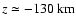 in the GMLT model.
The grid of mesh points of the simulated domain is
adjusted so that the w maxima of the 3D simulation and the GMLT coincide at
the same layer.
in the GMLT model.
The grid of mesh points of the simulated domain is
adjusted so that the w maxima of the 3D simulation and the GMLT coincide at
the same layer. |
Figures 1 and 2 present w(z),
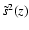 versus depth for the 3D simulation.
For comparison purpose, the plots also
show w and
versus depth for the 3D simulation.
For comparison purpose, the plots also
show w and
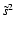 obtained
with the GMLT solar model.
obtained
with the GMLT solar model.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f2.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg99.gif) |
Figure 2:
Same as Fig. 1 for the
mean square of the entropy fluctuations (
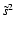 ).
The peak is narrower than for the velocity w because ).
The peak is narrower than for the velocity w because
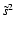 scales approximatively as w4.
scales approximatively as w4. |
The vertical velocity GMLT w is larger at the top of
superadiabatic region but smaller just
beneath compared to values from the simulation.
The GMLT
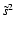 is larger than in
the simulation (
is larger than in
the simulation ( 20%). This explains that
the relative contribution of the entropy source term
to the excitation is overestimated
with the GMLT model
(see Sect. 4.1.1).
Differences between
the GMLT and the simulation are likely to be related to differences in
the convective efficiency: GMLT is less efficient than the 3D simulation.
Indeed as pointed out by Houdek & Gough (2002),
a single eddy approach such as the GMLT results in a larger
peak for the superadiabatic gradient.
20%). This explains that
the relative contribution of the entropy source term
to the excitation is overestimated
with the GMLT model
(see Sect. 4.1.1).
Differences between
the GMLT and the simulation are likely to be related to differences in
the convective efficiency: GMLT is less efficient than the 3D simulation.
Indeed as pointed out by Houdek & Gough (2002),
a single eddy approach such as the GMLT results in a larger
peak for the superadiabatic gradient.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f3.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg100.gif) |
Figure 3:
Same as Fig. 1
for the anisotropy factor  versus z.
versus z. |
3.3 Velocity anisotropy at large scale
As it will be shown in
Sect. 4.1.2,
the value of  plays a crucial role in controlling
the depth of the excitation region and therefore the total
amount of acoustic energy injected into the oscillation modes.
plays a crucial role in controlling
the depth of the excitation region and therefore the total
amount of acoustic energy injected into the oscillation modes.
Figure 3 displays the anisotropy factor
 versus depth z for the 3D simulation.
versus depth z for the 3D simulation.
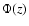 sharply decreases from the value
sharply decreases from the value 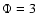 at the top
of the CZ down to
at the top
of the CZ down to 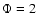 and then
slowly decreases to reach the value
and then
slowly decreases to reach the value
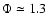 at the bottom of the simulation.
The decrease of
at the bottom of the simulation.
The decrease of 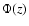 with depth
is explained first by the onset of the convection
and the formation of convective plumes
at
with depth
is explained first by the onset of the convection
and the formation of convective plumes
at 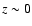 and then by the relative increase
in number of the plumes inward in the simulation.
Indeed, plumes are highly anisotropic structures
whereas turbulent cells are quite isotropic.
The turbulent Mach number increases with z and
reaches its maximum value at the top of the CZ.
Therefore the fluid is more turbulent outward in the atmosphere.
Consequently the number of turbulent isotropic cells increases
with z up to the top of the CZ whereas the number of plumes remains roughly constant. The medium is thus
more isotropic outward than inward.
and then by the relative increase
in number of the plumes inward in the simulation.
Indeed, plumes are highly anisotropic structures
whereas turbulent cells are quite isotropic.
The turbulent Mach number increases with z and
reaches its maximum value at the top of the CZ.
Therefore the fluid is more turbulent outward in the atmosphere.
Consequently the number of turbulent isotropic cells increases
with z up to the top of the CZ whereas the number of plumes remains roughly constant. The medium is thus
more isotropic outward than inward.
In most of the excitation region,
the value of 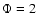 consistent with the BV-MLT
is in better agreement with the values
of
consistent with the BV-MLT
is in better agreement with the values
of 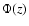 inferred from the simulation
compared to the value
inferred from the simulation
compared to the value
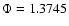 which must be imposed for the GMLT solar model
in order to match the observed solar damping rates.
which must be imposed for the GMLT solar model
in order to match the observed solar damping rates.
3.4 Turbulent kinetic energy spectrum E(k)
Variations of E and 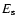 with k at different depths
z are depicted in Fig. 4.
The spectra clearly show two regimes:
at large scale (small values of k), the spectra
increase approximately as k+1 which can
roughly be explained using dimensional analysis.
At small scale (large values of k), the spectra
decrease very rapidly with k.
The Kolmogorov law (k -5/3) is observed only
over a small k-range.
Departures of the computed spectra from a Kolmogorov law
at high values of k can be explained by the finite resolution
of the simulation spatial grid.
with k at different depths
z are depicted in Fig. 4.
The spectra clearly show two regimes:
at large scale (small values of k), the spectra
increase approximately as k+1 which can
roughly be explained using dimensional analysis.
At small scale (large values of k), the spectra
decrease very rapidly with k.
The Kolmogorov law (k -5/3) is observed only
over a small k-range.
Departures of the computed spectra from a Kolmogorov law
at high values of k can be explained by the finite resolution
of the simulation spatial grid.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f4.eps}\par\includegraphics[width=8.8cm,clip]{3271f5.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg103.gif) |
Figure 4:
Turbulent kinetic energy spectra
E (top) and 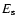 (bottom)
from the simulation are plotted versus k and
for different depths z in the simulation. The straight solid lines
delimitate the slopes k1 and k-5/3 of the EKS spectrum (Eq. (21)). Intersection
of the slopes determines k0E, the scale of maximum energy at each depth z.
(bottom)
from the simulation are plotted versus k and
for different depths z in the simulation. The straight solid lines
delimitate the slopes k1 and k-5/3 of the EKS spectrum (Eq. (21)). Intersection
of the slopes determines k0E, the scale of maximum energy at each depth z. |
The main characteristics of the kinetic spectrum E(k,z) - k dependency -
derived from the 3D simulation are approximatively reproduced
by an analytical expression which was considered by Musielak et al. (1994), namely
the "Extended Kolmogorov Spectrum'' (EKS hereafter)
defined in Musielak et al. (1994) as:
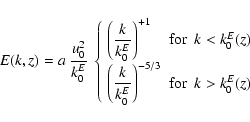 |
(21) |
where a is a normalisation factor which satisfies Eq. (20)
and u0 is defined according to Eq. (20). k0E is the scale
of maximum energy in the energy spectrum.
At each layer, k0E is determined by imposing that the EKS, as defined above,
matches the turbulent spectrum E(k,z) calculated
from the simulation as well as possible.
This then fixes the z dependency
of k0E. A similar procedure is applied
for
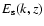 for which we introduce
for which we introduce
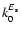 .
All spectra satisfy their respective normalisation
condition as given in Eq. (20).
.
All spectra satisfy their respective normalisation
condition as given in Eq. (20).
For comparison, in Fig. 7, the "Nesis Kolmogorov Spectrum'' (NKS hereafter) determined
from solar observations of Nesis et al. (1993) is also shown.
The NKS scales as k-5 in the energy injection region
for k < k0E and down to
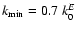 .
This spectrum does not agree with turbulent spectrum E(k,z) calculated from the simulation.
In particular, the NKS underestimates the
velocity of the small size turbulent elements
in the cascade (k>k0) and
overestimates the velocity of the turbulent
with wavenumber
.
This spectrum does not agree with turbulent spectrum E(k,z) calculated from the simulation.
In particular, the NKS underestimates the
velocity of the small size turbulent elements
in the cascade (k>k0) and
overestimates the velocity of the turbulent
with wavenumber
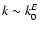 .
As we will show in Sect. 4.2, differences
between the EKS and the NKS have an important impact on
.
As we will show in Sect. 4.2, differences
between the EKS and the NKS have an important impact on 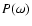 .
.
If we assume that
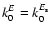 ,
one can show that
,
one can show that 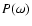 scales as k0-4.
scales as k0-4.
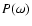 is therefore very dependent on the values
reached by k0(z) in the excitation region.
Variation of k0(z) with depth is thus shown in Fig. 5
for E and
is therefore very dependent on the values
reached by k0(z) in the excitation region.
Variation of k0(z) with depth is thus shown in Fig. 5
for E and 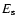 :
:
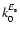 and
and
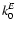 vary slowly within the excitation region.
vary slowly within the excitation region.
For comparison, in Fig. 5 we have also
plotted
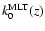 ,
the
MLT value for k0(z) according to
Eq. (12).
The scaling parameter
,
the
MLT value for k0(z) according to
Eq. (12).
The scaling parameter 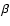 in the definition of
in the definition of
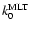 is determined such that
is determined such that
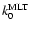 and
and
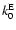 take the same value
at the layer
take the same value
at the layer
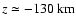 where w reaches
its maximum (and consequently the layer where the excitation is maximum).
The derived value is
where w reaches
its maximum (and consequently the layer where the excitation is maximum).
The derived value is
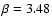 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f6.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg112.gif) |
Figure 5:
The wavenumbers k0E (solid line) and
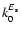 (dashed line)
are plotted versus z (k0E and
(dashed line)
are plotted versus z (k0E and
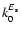 are obtained by
fitting, at each layer, the EKS (Eq. 21)
to the computed spectra E and
are obtained by
fitting, at each layer, the EKS (Eq. 21)
to the computed spectra E and 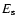 of Fig. 4 resp., see text for details).
The dotted line corresponds to
of Fig. 4 resp., see text for details).
The dotted line corresponds to
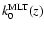 obtained
according to Eq. (12). In computing
obtained
according to Eq. (12). In computing
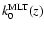 ,
we assume ,
we assume
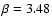 in order for
in order for
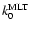 to match
the value reached by
to match
the value reached by
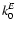 (solid line)
at the layer
(solid line)
at the layer
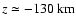 where w reaches
its maximum (
where w reaches
its maximum (
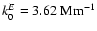 at that layer).
at that layer). |
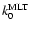 varies slowly with depth below the top of
the superadiabatic region (
varies slowly with depth below the top of
the superadiabatic region (
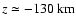 )
but
increases very rapidly above.
Such a behavior is explained by the rapid decrease
with z of the pressure scale height
)
but
increases very rapidly above.
Such a behavior is explained by the rapid decrease
with z of the pressure scale height 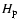 (which enters in the definition of
(which enters in the definition of
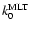 ,
Eq. (12))
in the atmosphere.
,
Eq. (12))
in the atmosphere.
Comparison between
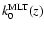 and
k0E(z) shows that the mixing-length
approach does not model satisfactorily the
behavior of
k0E(z) in particular
just above the layer at which w reaches its maximum value.
Consequences in terms of mode excitation
are investigated in Sect. 4.3.
and
k0E(z) shows that the mixing-length
approach does not model satisfactorily the
behavior of
k0E(z) in particular
just above the layer at which w reaches its maximum value.
Consequences in terms of mode excitation
are investigated in Sect. 4.3.
4 Consequences in term of p modes excitation
The acoustic energy supply rate P
injected into the solar oscillations is related to the rms value 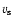 of surface velocity as:
of surface velocity as:
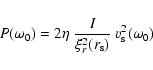 |
(22) |
where 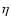 is the mode damping rate and
is the mode damping rate and
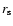 is the radius at which oscillations are measured.
is the radius at which oscillations are measured.
We derive the "observed'' P from Chaplin et al. (1998)'s seismic
data according to Eq. (22) where the mode damping rate, 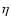 ,
and the mode surface velocity,
,
and the mode surface velocity, 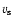 ,
are obtained from Chaplin et al. (1998)'s data. The mode mass
,
are obtained from Chaplin et al. (1998)'s data. The mode mass
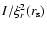 is given by
the GMLT model and we adopt
is given by
the GMLT model and we adopt
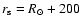 km
consistent with the observations.
km
consistent with the observations.
Theoretical values of P are computed according to Eq. (1).
In Eqs. (10) and (11)
the integrations over k are performed
from
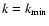 (where
(where
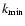 depends
on the adopted turbulent spectra E and
depends
on the adopted turbulent spectra E and 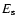 )
to
k=20 k0.
We checked numerically that
contributions to the excitation rate from turbulent elements
with
)
to
k=20 k0.
We checked numerically that
contributions to the excitation rate from turbulent elements
with
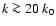 are negligible.
are negligible.
A Gaussian function is assumed for
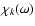 in Eq. (10) and Eq. (11).
in Eq. (10) and Eq. (11).
For the other quantities (w,
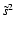 ,
,
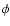 ,
k0, E(k/k0) and
,
k0, E(k/k0) and
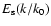 )
involved in the expression for P we investigate several possible assumptions.
)
involved in the expression for P we investigate several possible assumptions.
4.1 Convective velocities and large scale anisotropy
In this section, the excitation rate P (Eq. (1))
is computed with the following assumptions:
- the k-dependency E and 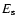 is given by the analytical form
of Eq. (21), also called the EKS.
is given by the analytical form
of Eq. (21), also called the EKS.
-
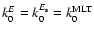 where
where
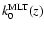 is given in Eq. (12)
with
is given in Eq. (12)
with
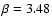 so that
so that
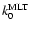 takes the
value reached by
k0E(z) (solid line, Fig. 5)
at the layer
takes the
value reached by
k0E(z) (solid line, Fig. 5)
at the layer
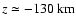 where w reaches its maximum.
where w reaches its maximum.
For the quantities  ,
w and
,
w and
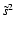 we investigate the effects of using either
the values derived from the 3D simulation (see Sects. 3.2 and 3.3) or calculated
with the GMLT solar model.
we investigate the effects of using either
the values derived from the 3D simulation (see Sects. 3.2 and 3.3) or calculated
with the GMLT solar model.
4.1.1 Convective velocities and entropy fluctuations
The values of w,
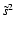 and
and 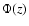 are fixed by the 3D simulation inside the simulation
domain and by the 1D equilibrium model outside this domain.
Either, if we impose zero values
or if we assume quantities from the 1D MLT model,
no sensitivity on the calculation of P is found.
are fixed by the 3D simulation inside the simulation
domain and by the 1D equilibrium model outside this domain.
Either, if we impose zero values
or if we assume quantities from the 1D MLT model,
no sensitivity on the calculation of P is found.
Results are shown in Fig. 6 for P and for
the relative contribution of the Reynolds stress
to the total energy supply rate P. When the excitation rate 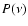 is
computed with quantities derived from the 3D simulation as described in
Sect. 2.3, the resulting
excitation rate at maximum is found too small by a factor
is
computed with quantities derived from the 3D simulation as described in
Sect. 2.3, the resulting
excitation rate at maximum is found too small by a factor  4
compared with the observations.
4
compared with the observations.
Provided the appropriate value for  is given
in the GMLT estimations (see Sect. 4.1.2 below),
no significant difference is found
in the excitation rate when computed with the values of w and
is given
in the GMLT estimations (see Sect. 4.1.2 below),
no significant difference is found
in the excitation rate when computed with the values of w and
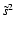 from the simulation
or their respective GMLT estimations.
from the simulation
or their respective GMLT estimations.
The main effect is illustrated in the bottom panel of Fig. 6:
the 3D simulation generates a
larger relative contribution of the Reynolds stress
to P than the GMLT model. This is explained as follows:
within most part of the excitation region - except at the top of
superadiabatic region - the values reached by w are larger
whereas values reached by
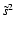 are smaller than their corresponding GMLT estimations.
are smaller than their corresponding GMLT estimations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f7.eps}\par\includegraphics[width=8.8cm,clip]{3271f8.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg127.gif) |
Figure 6:
Top: Rate P at which acoustic energy
is injected into the solar radial modes.
The filled dots represent P computed from Chaplin et al. (1998)'s
solar seismic data according to Eq. (22).
The curves represent theoretical values of
P computed according Eq. (1)
and for different computations of w,
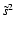 and
and 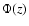 :
Solid line: values of w, :
Solid line: values of w,
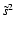 and
and 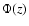 are fixed by the 3D simulation inside the simulated
domain and by the 1D equilibrium model outside this domain.
Dashed line (- - -): same as solid line but
fixing
are fixed by the 3D simulation inside the simulated
domain and by the 1D equilibrium model outside this domain.
Dashed line (- - -): same as solid line but
fixing  to BV's value
to BV's value 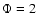 .
Dot dashed line ( .
Dot dashed line (
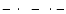 ):values of
w, ):values of
w,
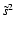 and
and 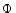 (=1.37)
are fixed by the 1D equilibrium model (GMLT).
Three dots dashed line ( (=1.37)
are fixed by the 1D equilibrium model (GMLT).
Three dots dashed line (
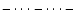 ): same as
the dot dashed line but fixing ): same as
the dot dashed line but fixing  to BV's value
to BV's value 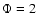 .
Bottom: Same as top panel for the relative
contribution of the Reynolds stress, .
Bottom: Same as top panel for the relative
contribution of the Reynolds stress, 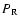 ,
to the total acoustic energy P. ,
to the total acoustic energy P. |
4.1.2 Velocity anisotropy at large scales
The main consequence (in term of p modes excitation) of the
differences between the time averaged properties of the convective region
inferred from the 3D simulation and from the GMLT solar model (Fig. 6)
is due to differences in their respective anisotropy factor
 values (Fig. 3).
values (Fig. 3).
Within most of the excitation region, 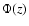 is found
close to
is found
close to  2 and thus larger than the value
2 and thus larger than the value 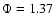 assumed for the 1D equilibrium model
(see Sect. 3.3
and Fig. 3).
Smaller values of
assumed for the 1D equilibrium model
(see Sect. 3.3
and Fig. 3).
Smaller values of  decrease
the rms total convective velocity which results in larger values of
decrease
the rms total convective velocity which results in larger values of
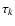 (see Eqs. (14), (15))
and therefore in a smaller depth of excitation
for a given mode frequency (see Paper III for more details).
Smaller values of the rms total convective velocity
also induce smaller values of
E in the integrand of Eq. (1).
Consequently, as it is
illustrated in Fig. 6,
the total amount of acoustic energy injected into the modes
is
(see Eqs. (14), (15))
and therefore in a smaller depth of excitation
for a given mode frequency (see Paper III for more details).
Smaller values of the rms total convective velocity
also induce smaller values of
E in the integrand of Eq. (1).
Consequently, as it is
illustrated in Fig. 6,
the total amount of acoustic energy injected into the modes
is  5 times smaller for the constant
value
5 times smaller for the constant
value 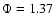 compared to the constant
value
compared to the constant
value 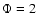 (the relative contribution of the Reynolds stress to P is
found
(the relative contribution of the Reynolds stress to P is
found  2 times larger in the simulation).
2 times larger in the simulation).
The effect of the depth dependency of  on
the mode excitation is small except at high frequency.
This is illustrated in the bottom panel
of Fig. 6 (compare the solid line with the dashed line).
Just above the top of the superadiabatic region
(
on
the mode excitation is small except at high frequency.
This is illustrated in the bottom panel
of Fig. 6 (compare the solid line with the dashed line).
Just above the top of the superadiabatic region
(
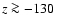 km),
km),
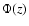 increases rapidly with z
until the value
increases rapidly with z
until the value 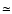 3 (Fig. 3). Most of the
injection of acoustic energy into the high
frequency modes occurs at the top of superadiabatic region.
The high frequency modes are therefore
more sensitive to this rapid increase of
3 (Fig. 3). Most of the
injection of acoustic energy into the high
frequency modes occurs at the top of superadiabatic region.
The high frequency modes are therefore
more sensitive to this rapid increase of 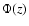 .
As a
consequence, the relative contribution
of the Reynolds stress is larger for the
high frequency modes than it is
when assuming the constant value
.
As a
consequence, the relative contribution
of the Reynolds stress is larger for the
high frequency modes than it is
when assuming the constant value 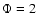 .
.
4.2 Turbulent spectra
In this section we compare
the excitation rate obtained assuming, for the turbulent spectra
(E and 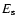 )
either - the EKS spectrum (Eq. (21)) with slopes given by the 3D simulation
as in the previous section - or
assuming the NKS spectrum from solar observations of Nesis et al. (1993)
(see also Paper I).
)
either - the EKS spectrum (Eq. (21)) with slopes given by the 3D simulation
as in the previous section - or
assuming the NKS spectrum from solar observations of Nesis et al. (1993)
(see also Paper I).
As in Sect. 4.1
we compute P
using w,
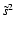 and
and  derived
from the 3D simulation and assuming that
derived
from the 3D simulation and assuming that
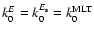 .
The results are plotted in Fig. 8.
.
The results are plotted in Fig. 8.
The NKS overestimates the maximum in P by a
factor  1.5 while the EKS underestimates it by a factor
1.5 while the EKS underestimates it by a factor  4.
This is because most of the kinetic energy in the
NKS is concentrated at
4.
This is because most of the kinetic energy in the
NKS is concentrated at
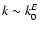 whereas
in the EKS a large part of the energy is concentrated both at large scales (k < k0E)
and at small scales (k > k0E).
whereas
in the EKS a large part of the energy is concentrated both at large scales (k < k0E)
and at small scales (k > k0E).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f9.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg131.gif) |
Figure 7:
The NKS and the EKS
turbulent kinetic energy
spectra are plotted versus the normalized
wavenumber k/k0. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f10.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg132.gif) |
Figure 8:
Acoustic energy supply rate P computed according to Eq. (1) and assuming for E(k) the EKS and the NKS plotted in Fig. 7. Dots represent the energy supply rate injected into the oscillations derived from the solar observations with the help of Eq. (22). |
4.3 Effects due to the stratification of the turbulent spectrum at
large scale
In Sect. 3.4
we showed that the variations of
k0E and
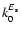 with z deduced from the 3D simulation differ
from the MLT estimation as given by Eq. (12)
(see Fig. 5). Figure 9
presents the consequences
of the z variations of k0E on the oscillation amplitudes (as the variations of k0Eand
with z deduced from the 3D simulation differ
from the MLT estimation as given by Eq. (12)
(see Fig. 5). Figure 9
presents the consequences
of the z variations of k0E on the oscillation amplitudes (as the variations of k0Eand
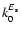 with depth are quite similar we assume for the sake of simplicity that
with depth are quite similar we assume for the sake of simplicity that
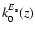 is equal to
k0E(z)).
is equal to
k0E(z)).
The z dependency of k0E causes the maximum of P to be
larger than when assuming
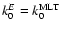 (
( 50% larger). This is due to the fact
that in most part of the excitation region
50% larger). This is due to the fact
that in most part of the excitation region
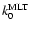 is smaller than k0E and
is smaller than k0E and
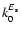 except above the top of the superadiabatic
region (see Fig. 5).
A larger k0E results in a larger linewidth
except above the top of the superadiabatic
region (see Fig. 5).
A larger k0E results in a larger linewidth
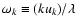 for
for
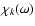 hence in a larger amount of acoustic energy
injected to the mode (see Eq. (13)).
hence in a larger amount of acoustic energy
injected to the mode (see Eq. (13)).
Furthermore, at high frequency, P decreases with 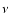 more rapidly than when assuming
more rapidly than when assuming
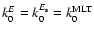 .
Taking into account the actual variation k0E with z instead of assuming
.
Taking into account the actual variation k0E with z instead of assuming
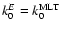 makes then the
makes then the 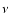 -dependency of P at high frequency closer to that of the observed excitation spectrum. This is because, above the top of the superadiabatic region, k0E decreases with z whereas
-dependency of P at high frequency closer to that of the observed excitation spectrum. This is because, above the top of the superadiabatic region, k0E decreases with z whereas
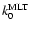 increases with z.
Indeed, the excitation of the high frequency modes occurs predominantly in the upper most part of the top of the superadiabatic
region. As mentionned above the line width of
increases with z.
Indeed, the excitation of the high frequency modes occurs predominantly in the upper most part of the top of the superadiabatic
region. As mentionned above the line width of
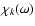 decreases with decreasing k0. Therefore the contribution of the term
decreases with decreasing k0. Therefore the contribution of the term
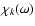 to the excitation of high frequency mode is smaller when assuming the actual variation of k0E with z than when assuming that k0E varies as
to the excitation of high frequency mode is smaller when assuming the actual variation of k0E with z than when assuming that k0E varies as
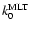 .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3271f11.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg137.gif) |
Figure 9:
Same as Fig. 6.
Solid line: the variation of k0E and
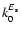 with z are obtained from the simulation (see Fig. 5 and Sect. 3.4).
The dashed line is identical to the solid line of Fig. 6 where
with z are obtained from the simulation (see Fig. 5 and Sect. 3.4).
The dashed line is identical to the solid line of Fig. 6 where
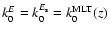 . . |
5 Summary and discussion
An analysis of a 3D simulation of the upper part
of the solar convective zone provides
time averaged constraints upon several physical parameters
which enter the theoretical expression for
the supply rate of energy, P, injected
into the solar p modes. These constraints are:
1) the depth dependency: of u2, the mean square velocity - of
w2, the mean square vertical component of the velocity - of
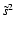 ,
the mean square values of entropy fluctuations.
,
the mean square values of entropy fluctuations.
2) the wavenumber (k) dependency of E and 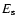 the turbulent kinetic energy spectrum and the turbulent entropy spectrum
respectively.
the turbulent kinetic energy spectrum and the turbulent entropy spectrum
respectively.
3) the depth dependency of the
wavenumbers k0E and
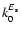 ,
the wavenumbers at which convective energy is maximum and
is injected into the turbulent inertial ranges of
the turbulent kinetic energy spectra E,
,
the wavenumbers at which convective energy is maximum and
is injected into the turbulent inertial ranges of
the turbulent kinetic energy spectra E, 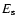 respectively.
respectively.
4) the depth dependency of
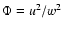 ,
the mean values of the anisotropy.
,
the mean values of the anisotropy.
Differences between w2 - and
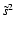 -
and their respective GMLT estimations have only small consequences on
the profile of the excitation rate
-
and their respective GMLT estimations have only small consequences on
the profile of the excitation rate 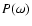 .
However the values reached by w2 and
.
However the values reached by w2 and
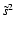 with the 3D simulation
are responsible for an increase of the
relative contribution of the Reynolds stress
to
with the 3D simulation
are responsible for an increase of the
relative contribution of the Reynolds stress
to 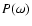 by a factor
by a factor  1.5 at low frequency
1.5 at low frequency
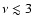 mHz compared to the one
obtained with the GMLT solar model.
This is because the GMLT model
overestimates
mHz compared to the one
obtained with the GMLT solar model.
This is because the GMLT model
overestimates
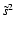 by
by  20% at the top of excitation
region and underestimates w2 within
most part of the excitation region by up to
20% at the top of excitation
region and underestimates w2 within
most part of the excitation region by up to  15%.
15%.
The energy distributions E and 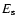 over eddies with
wavenumber k obtained in the simulation
scale approximately as k+1in the domain
over eddies with
wavenumber k obtained in the simulation
scale approximately as k+1in the domain
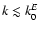 .
They therefore have
approximately the same behavior
as the "Extended Kolmogorov Spectrum''
(EKS) defined in Musielak et al. (1994).
In contrast, their k-dependencies
significantly differ from those assumed
in the Nesis Kolmogorov Spectrum (NKS) which
scales as k-5 below k0E.
The NKS predicts much larger maximum values for P
than does the EKS.
This is because the NKS
concentrates kinetic energy in the vicinity of k0E.
.
They therefore have
approximately the same behavior
as the "Extended Kolmogorov Spectrum''
(EKS) defined in Musielak et al. (1994).
In contrast, their k-dependencies
significantly differ from those assumed
in the Nesis Kolmogorov Spectrum (NKS) which
scales as k-5 below k0E.
The NKS predicts much larger maximum values for P
than does the EKS.
This is because the NKS
concentrates kinetic energy in the vicinity of k0E.
The 3D simulation indicates that
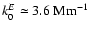 at the top of excitation region.
This corresponds to the horizontal size of the granulation
(
at the top of excitation region.
This corresponds to the horizontal size of the granulation
( 2 Mm). It is worth noting that taking the depth dependency of
k0(z) into account results in a increase
of the maximum of P by as much as
2 Mm). It is worth noting that taking the depth dependency of
k0(z) into account results in a increase
of the maximum of P by as much as  50%
and brings these values even closer to the observations.
On the other hand, only minor differences are seen
on the frequency dependence
of the excitation rates P when
using the depth dependency
of k0(z) from the simulation or
assuming the form
50%
and brings these values even closer to the observations.
On the other hand, only minor differences are seen
on the frequency dependence
of the excitation rates P when
using the depth dependency
of k0(z) from the simulation or
assuming the form
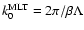 with
with
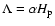 provided that
provided that 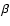 is adjusted in
order for
is adjusted in
order for
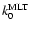 to match the value
reached by k0E at the layer where w reaches its maximum.
to match the value
reached by k0E at the layer where w reaches its maximum.
The excitation rate 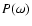 is
very sensitive to the value of
is
very sensitive to the value of  .
In the GMLT formulation,
the quantity
.
In the GMLT formulation,
the quantity  is a parameter which
is adjusted in order to obtain the best fit
between computed solar damping rates and the solar
measurements: the adopted value
is
is a parameter which
is adjusted in order to obtain the best fit
between computed solar damping rates and the solar
measurements: the adopted value
is 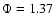 (see Houdek et al. 2001).
On the other hand, the 3D simulation suggests a higher value
within the excitation region (
(see Houdek et al. 2001).
On the other hand, the 3D simulation suggests a higher value
within the excitation region (
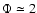 ).
Larger values of
).
Larger values of  result in an increase of the
mode driving by the turbulent motions.
We find that using the value
result in an increase of the
mode driving by the turbulent motions.
We find that using the value 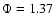 underestimates
underestimates
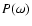 by a factor
by a factor
 5 relatively to
5 relatively to 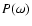 computed with
computed with 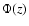 in the excitation region from the 3D simulation.
On the other hand, using the GMLT formulation for the convective velocity
with a value
in the excitation region from the 3D simulation.
On the other hand, using the GMLT formulation for the convective velocity
with a value 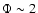 ,
as suggested by the 3D simulation, yields
a power
,
as suggested by the 3D simulation, yields
a power 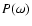 close to
the one obtained by the 3D simulation.
To fix ideas, the maximum amplitude
is
close to
the one obtained by the 3D simulation.
To fix ideas, the maximum amplitude
is  4 cm/s,
4 cm/s,  8 cm/s,
8 cm/s,  10 cm/s
when calculated with GMLT and
10 cm/s
when calculated with GMLT and 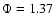 ,
with GMLT and
,
with GMLT and 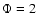 and when using velocities and
and when using velocities and 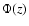 derived from
the 3 D simulation respectively. These figures must be compared to
the observed maximum amplitude
derived from
the 3 D simulation respectively. These figures must be compared to
the observed maximum amplitude  23 cm/s.
23 cm/s.
This shows that the values of
 found for the solar GMLT model when adjusted to the damping rates
is not compatible
with the actual properties of the turbulent medium
in the excitation region.
An improvement could come from a consistent calculation
which would assume a depth dependent
found for the solar GMLT model when adjusted to the damping rates
is not compatible
with the actual properties of the turbulent medium
in the excitation region.
An improvement could come from a consistent calculation
which would assume a depth dependent 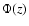 ,
as suggested by the simulations, in both damping rate and
excitation rate computations.
Damping rates are indeed expected to be sensitive to depths deeper than the
excitation rate where smaller values of
,
as suggested by the simulations, in both damping rate and
excitation rate computations.
Damping rates are indeed expected to be sensitive to depths deeper than the
excitation rate where smaller values of  are encountered
and the simulation shows that the velocity anisotropy factor
are encountered
and the simulation shows that the velocity anisotropy factor
 decreases from 2 down to 1.3 from top
of the superadiabatic region to bottom of the simulated
solar region.
decreases from 2 down to 1.3 from top
of the superadiabatic region to bottom of the simulated
solar region.
Without any adjustment of scaling parameters
but using all the constraints inferred from the 3D simulation considered here,
we find a maximum of P much
larger ( 5 times larger)
than the P maximum obtained
using a 1D GMLT solar model when
5 times larger)
than the P maximum obtained
using a 1D GMLT solar model when  is fixed by the observed
damping rates.
It is also found that the so-called
entropy source term, which arises from
the advection of the turbulent fluctuations
of entropy by the turbulent motions,
is still the dominant source of the excitation.
However its contribution to the excitation
is now
is fixed by the observed
damping rates.
It is also found that the so-called
entropy source term, which arises from
the advection of the turbulent fluctuations
of entropy by the turbulent motions,
is still the dominant source of the excitation.
However its contribution to the excitation
is now  65-75%
instead of
65-75%
instead of  95% as found in Paper II.
95% as found in Paper II.
Our computation still underestimates by a factor
 3 the maximum value of P compared with the one derived
from the solar seismic observations by Chaplin et al. (1998).
Moreover the decrease of P with
3 the maximum value of P compared with the one derived
from the solar seismic observations by Chaplin et al. (1998).
Moreover the decrease of P with 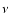 at
high frequency (
at
high frequency (
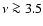 mHz) is
found to be significantly smaller
than the one inferred from
the solar seismic observations,
indicating a deficiency in the
present modelling at high frequency.
mHz) is
found to be significantly smaller
than the one inferred from
the solar seismic observations,
indicating a deficiency in the
present modelling at high frequency.
As a final point, we discuss the model for the
turbulent kinetic energy spectrum:
In Paper II the parameter 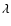 and k0E were adjusted - given a turbulent spectrum E(k) -
so as to obtain the best possible agreement
between computed and measured values of the
maximum solar oscillation amplitude
and its frequency position, as well as the frequency-dependence of the
oscillation amplitudes. Adjustments of these scaling parameters led to
a better agreement between computed values of P and the
seismic observations when using the NKS than the EKS.
However, the present results
from a 3D simulation strongly suggest that the
EKS is a better model for the solar turbulent kinetic energy spectrum.
and k0E were adjusted - given a turbulent spectrum E(k) -
so as to obtain the best possible agreement
between computed and measured values of the
maximum solar oscillation amplitude
and its frequency position, as well as the frequency-dependence of the
oscillation amplitudes. Adjustments of these scaling parameters led to
a better agreement between computed values of P and the
seismic observations when using the NKS than the EKS.
However, the present results
from a 3D simulation strongly suggest that the
EKS is a better model for the solar turbulent kinetic energy spectrum.
The better agreement obtained with NKS than EKS when adjusting the free
parameters is due to the fact that the NKS concentrates
most of the kinetic energy in the vicinity of k0E.
Indeed, the NKS predominantly excites
the modes whose period are close to the
characteristic lifetime of the eddies of wavenumber
k0E, i.e. the modes with frequency close to the
frequency at which P peaks (
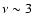 mHz).
As a consequence, the amount of energy going into the
high frequency modes is relatively smaller with the NKS
than it is with the EKS. This explains why the NKS reproduces
better the steep decrease with
mHz).
As a consequence, the amount of energy going into the
high frequency modes is relatively smaller with the NKS
than it is with the EKS. This explains why the NKS reproduces
better the steep decrease with 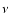 of P
at high frequency and results in a value
for k0E identical to that inferred
from the simulation (
of P
at high frequency and results in a value
for k0E identical to that inferred
from the simulation (
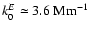 ).
In contrast, whatever the adjustment,
the EKS reproduces neither
the frequency dependence of P at high frequency nor
the value
).
In contrast, whatever the adjustment,
the EKS reproduces neither
the frequency dependence of P at high frequency nor
the value
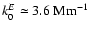 .
Hence assuming that the 3D simulation yields
the proper behavior of the solar
kinetic energy spectrum, well modelled by the EKS,
one is led to conclude that the excitation as given by the present
stochastic excitation model is not efficient enough at
large scales (
.
Hence assuming that the 3D simulation yields
the proper behavior of the solar
kinetic energy spectrum, well modelled by the EKS,
one is led to conclude that the excitation as given by the present
stochastic excitation model is not efficient enough at
large scales (
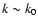 )
and too efficient at small scales (k > k0).
)
and too efficient at small scales (k > k0).
Discrepancies between our calculations and the observed excication rates or the results by Stein & Nordlund (2001) are
likely due to dynamic properties of
turbulence which are not properly taken into account in the excitation model.
Indeed, the dynamic properties of turbulence are modeled by the function 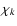 .
All current theoretical calculations of the excitation rates assume a Gaussian function for
.
All current theoretical calculations of the excitation rates assume a Gaussian function for 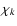 (e.g. Goldreich & Keeley 1977; Balmforth 1992a).
The Gaussian model is likely to be at the origin of the current under-estimate of the rates at which solar p-modes are excited (see forthcoming paper Samadi et al. 2003).
This may also explain the fact that we find that the
entropy source term is dominant over the Reynolds stress
contribution whereas Stein & Nordlund (2001) in their
direct computations found the reverse.
In a recent study based on a frequency analysis of the present simulation we investigate what model can correctly reproduce model
(e.g. Goldreich & Keeley 1977; Balmforth 1992a).
The Gaussian model is likely to be at the origin of the current under-estimate of the rates at which solar p-modes are excited (see forthcoming paper Samadi et al. 2003).
This may also explain the fact that we find that the
entropy source term is dominant over the Reynolds stress
contribution whereas Stein & Nordlund (2001) in their
direct computations found the reverse.
In a recent study based on a frequency analysis of the present simulation we investigate what model can correctly reproduce model 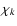 in the frequency range where the acoustic energy injected into the solar p-modes is important (see forthcoming paper Samadi et al. 2003).
in the frequency range where the acoustic energy injected into the solar p-modes is important (see forthcoming paper Samadi et al. 2003).
In the manner of Rosenthal et al. (1999) constraints from 3D simulation can be imposed to the 1D model.
According to the authors, such constraints result in a better agreement between the observed frequencies of the solar p-modes and the eigenfrequencies of the computed adiabatic oscillations.
An improvement in the calculation of the excitation rates at solar-type oscillations could then also come from a more consistent calculation of the eigenmodes which would use such constrained 1D model.
Acknowledgements
We thank H.-G. Ludwig for valuable help in analyzing the simulated data.
We are indebted to G. Houdek for providing us the solar model.
We thank the referee (B. Dintrans) for his meaningful comments.
RS's work has been supported in part by the Particle Physics and
Astronomy Research Council of the UK under grant PPA/G/O/1998/00576.
-
Baglin, A., & The Corot Team. 1998, in New Eyes to See Inside the Sun and Stars, IAU Symp., 185, 301
-
Balmforth, N. J. 1992a, MNRAS, 255, 639
NASA ADS
-
Balmforth, N. J. 1992b, MNRAS, 255, 603
NASA ADS
-
Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108
NASA ADS
-
Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550
NASA ADS
-
Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295
NASA ADS
-
Chaplin, W. J., Elsworth, Y., Isaak, G. R., et al. 1998, MNRAS, 298, L7
NASA ADS
-
Christensen-Dalsgaard, J. 1982, MNRAS, 199, 735
NASA ADS
-
Eggleton, P. P., Faulkner, J., & Flannery, B. P. 1973, A&A, 23, 325
NASA ADS
-
Favata, F., Roxburgh, I., & Christensen-Dalsgaard, J. 2000, in The Third MONS Workshop: Science Preparation and Target Selection, 49
-
Goldreich, P., & Keeley, D. A. 1977, ApJ, 212, 243
NASA ADS
-
Goldreich, P., Murray, N., & Kumar, P. 1994, ApJ, 424, 466
NASA ADS
-
Gough, D. O. 1977, ApJ, 214, 196
NASA ADS
-
Houdek, G. 1996, Ph.D. Thesis, Institut für Astronomie, Wien
-
Houdek, G., Balmforth, N. J., Christensen-Dalsgaard, J., & Gough, D. O. 1999, A&A, 351, 582
NASA ADS
-
Houdek, G., Chaplin, W. J., Appourchaux, T., et al. 2001, MNRAS, 327, 483
NASA ADS
-
Houdek, G., & Gough, D. O. 2002, MNRAS, 336, L65
NASA ADS
-
Musielak, Z. E., Rosner, R., Stein, R. F., & Ulmschneider, P. 1994, ApJ, 423, 474
NASA ADS
-
Nesis, A., Hanslmeier, A., Hammer, R., et al. 1993, A&A, 279, 599
NASA ADS
-
Nordlund, A., Spruit, H. C., Ludwig, H. G., & Trampedach, R. 1997, A&A, 328, 229
NASA ADS
-
Osaki, Y. 1990, in Lecture Notes in Physics: Progress of Seismology of the Sun and Stars, ed. Y. Osaki, & H. Shibahashi (Springer-Verlag), 75
-
Rieutord, M., Roudier, T., Malherbe, J. M., & Rincon, F. 2000, A&A, 357, 1063
NASA ADS
-
Rosenthal, C. S., Christensen-Dalsgaard, J., Nordlund, Å., Stein, R. F., & Trampedach, R. 1999, A&A, 351, 689
NASA ADS
-
Samadi, R. 2001, in SF2A-2001: Semaine de l'Astrophysique Francaise, E148 [astro-ph/0108363]
-
Samadi, R., & Goupil, M. 2001, A&A, 370, 136 (Paper I)
NASA ADS
-
Samadi, R., Goupil, M., & Lebreton, Y. 2001, A&A, 370, 147 (Paper II)
NASA ADS
-
Samadi, R., Houdek, G., Goupil, M.-J., & Lebreton, Y. 2002, A&A, submitted (Paper III)
-
Samadi, R., Nordlund, Å., Stein, R., Goupil, M.-J., & Roxburgh, I. 2003, A&A, in press
-
Stein, R. F. 1967, Sol. Phys., 2, 385
NASA ADS
-
Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914
NASA ADS
-
Stein, R. F., & Nordlund, Å. 2001, ApJ, 546, 585
NASA ADS
-
Unno, W., & Spiegel, E. A. 1966, PASJ, 18, 85
NASA ADS
Copyright ESO 2003
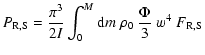
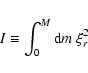
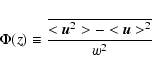
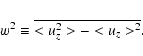
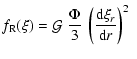
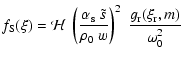
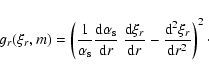
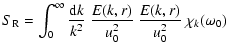
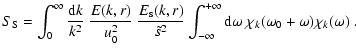
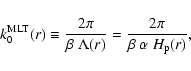
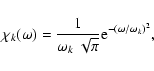
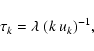
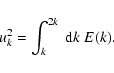
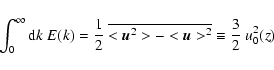
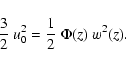
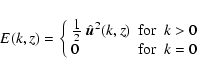
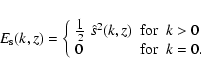
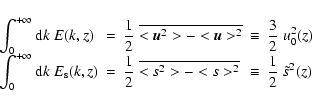
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f1.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f2.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg99.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f3.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f4.eps}\par\includegraphics[width=8.8cm,clip]{3271f5.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg103.gif)
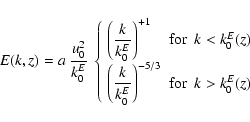
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f6.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg112.gif)
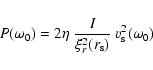
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f7.eps}\par\includegraphics[width=8.8cm,clip]{3271f8.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg127.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f9.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg131.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3271f10.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg132.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3271f11.eps}\end{figure}](/articles/aa/full/2003/19/aa3271/Timg137.gif)