Contents

A&A 403, 329-337 (2003)
DOI: 10.1051/0004-6361:20030355

A rigorous comparison of different planet detection algorithms

B. Tingley

Institut for Fysik og Astronomi (IFA), Aarhus Universitet, Ny Munkegade, Bygning 520, 8000 Aarhus C, Denmark

Received 27 August 2002 / Accepted 7 March 2003

Abstract
The idea of finding extrasolar planets (ESPs) through observations of drops in stellar brightness due to transiting objects has been around for decades. It has only been in the last ten years, however, that any serious attempts to find ESPs became practical. The discovery of a transiting planet around the star HD 209458 (Charbonneau et al. 2000) has led to a veritable explosion of research, because the photometric method is the only way to search a large number of stars for ESPs simultaneously with current technology. To this point, however, there has been limited research into the various techniques used to extract the subtle transit signals from noise, mainly brief summaries in various papers focused on publishing transit-like signatures in observations. The scheduled launches over the next few years of satellites whose primary or secondary science missions will be ESP discovery motivates a review and a comparative study of the various algorithms used to perform the transit identification, to determine rigorously and fairly which one is the most sensitive under which circumstances, to maximize the results of past, current, and future observational campaigns.

Key words: stars: planetary systems - occultations - methods: data analysis

1 Introduction

Struve (1952) was the first to postulate that ESPs could be found in the event that they transited their parent stars, which would dim slightly as the ESP occulted some of the light. This possibility was further explored and developed first by Rosenblatt (1971) and later by Borucki & Summers (1984). Due to technological restraints, the first serious observational attempts were not performed until Doyle et al. (1996), who observed the main-sequence eclipsing binary CM Draconis for the tell-tale photometric dips that would indicate the presence of a planet. This system has several qualities that make it an excellent choice for a planet search, discussed in more detail in Schneider & Doyle (1995). First of all, both members are low-mass main sequence dwarfs, which means that they are physically smaller than a typical field star of comparable apparent magnitude. This leads, in turn, to deeper transits. Additionally, the orbital plane of a planet in a binary system is probably going to be very close to the orbital plane of the stars, increasing the chance that a planet would cause observable transits. (Barbieri et al. 2002). Other projects besides this single, on-going observational campaign began over the next few years, such as STARE (Brown & Charbonneau 2000) and VULCAN (Borucki et al. 2001), which used dedicated small telescopes with large fields of view to observe thousands of stars simultaneously. This area of research became much more active after the discovery of the planet around HD 209458 (Charbonneau et al. 2000) and many projects were initiated in the hopes of witnessing an ESP as it transited its parent star. Among these are several future satellite projects that list ESP searches as either primary or secondary goals (COROT, Eddington, Kepler, and MONS to name a few) and HST observations of 47 Tuc (Gilliland et al. 2000). These observations of 47 Tuc - like all of the recent and ongoing projects - observed a few transit-like events. All of these events, with one exception, proved to be grazing eclipses of binary stars after follow-up observations. This one exception was discovered by the OGLE group, who were ostensibly searching for optical gravitational lenses towards the LMC. They observed 59 transit-like signatures in foreground Milky Way stars, most of which repeated (Udalski et al. 2002). Of these 59, only one so far has proven in the end to be an ESP (Konacki et al. 2003).

Statistics gathered from high-precision spectroscopic searches for ESPs among F, G, K and M field stars suggest that approximately 1% of the observed objects have giant planets with a period of three to six days. If one considers that around 10% of all possible orbital orientations of short-period giant planets would produce observable transits, the expected frequency of detections becomes about one planet per 3000 stars (Borucki et al. 2001), provided the effects of daytime and the three transit requirement are included. If this is so, the paucity of detections from these various searches is slightly puzzling. It is understandable, perhaps, that ESPs in clusters could be influenced by the dense environment there, affecting planet formation and retention - but not all of the observing campaigns have been towards clusters. It is also possible that a statistical prediction of a small number of ESPs could results in no detections. However, the results from the OGLE survey, which has only one confirmed ESP out of 50 000 stars (Konacki et al. 2003), suggest that the expected frequency of detections determined by Borucki et al. is probably too optimistic.

There are, however, other factors that could affect planet detection. For example, a poorly conceived or implemented differential photometric reduction could increase S/N, hiding transits that would otherwise be detectable. Likewise, the algorithms used to pick the transits out of noise can also have a strong influence on the number of detections. In fact, the work of the OGLE group reveals the effect that improvements in detections algorithms can have. In their first report on the transit-like events from their observing campaign, they identified 46 events with an in-house algorithm described only as a "cross-correlation'' (Udalski et al. 2002). Soon afterwards, they published an update (Udalski et al. 2002) listing 59 events - the new ones identified with an improved algorithm, the BLS technique described by Kovács et al. (2002). There are many algorithms, called detectors in signal processing literature, which can extract signals from data. Therefore, it is possible that the seeming scarcity of photometric ESPs could be caused, at least in part, by the detectors used.

With this possibility raised, a review of the different techniques used for transit identification is overdue, as is a comparative analysis to test the various techniques and to determine which is best under which conditions. Considering the current and future projects that plan to search for ESPs using photometry, this is a rather important line of research, one which has not been adequately addressed in the literature to this point, despite a certain amount of debate on the topic. This study, and future studies along this line, could potentially have a large impact on photometric ESP searches, since pushing the high-confidence detection limit down even a fraction could potentially reveal transits that would otherwise remain unidentified, shrouded in noise.

1.1 Transit characteristics

A planetary transit leaves a very specific signature on the light curve of a star. As the planet passes across the disk of its parents star, it occults some of the light. This results in a slight drop in the overall brightness of the system. The details of the resulting light curve can easily be calculated to fairly high precision using a basic limb-darkening law, but it is in fact very well represented by a simple square well. The depth of the well can be as much as one or two percent or more, defined approximately by the ratio of the area of the disk of the ESP and the area of the disk of the parent star. For example, a transit of Jupiter across the Sun would cause a drop in brightness of about 1% - about a hundredth of a magnitude. The width of the well is defined by the duration of the transit, which is generally somewhere between 3 and 6 hours for short period planets. This value depends not only on orbital velocity and radius but also on the impact parameter of the transits, i.e. how close the ESP's path across the disk of its parent star comes to the center of the star.

Planet search campaigns using the photometric technique are far more likely to discover short-period giant planets. Shortening the period produces more transits in a given period of time, as well as increasing the chance that a random orbital orientation will produce an observable transit. This geometrical effect goes as the inverse of the planetary orbital radius, or, using Kepler's third law, the period of the orbit to the $-\frac{2}{3}$. This means that, for example, placing Earth in Mercury's orbit would increase the chance of transit by a factor of 2.5, while moving it to an orbit with a period of 7 days would increase it by a factor of 14. To skew matters even more in the favor of short-period planets, short-period giant planets will in theory be inflated by incident radiation (Guillot et al. 1996). This conclusion is supported by the derived characteristics of both the planet around HD 209468 (Burrows et al. 2000) and OGLE-TR-56 (Konacki et al. 2003). This means that a short-period planet should be larger than an equally-massed planet further from the parent star and will therefore create deeper transits.

2 Transit identification algorithms

A transit identification algorithm is a mathematical tool that examines light curves for the presence of transits. In general, this is done by generating a test statistic (T) for each set of free parameters in some fashion or another. If this test statistic exceeds a certain value determined by the desired level of confidence that the event is not a chance occurrence of noise ($\eta$), then the algorithm decides that there is a transit-like event in the light curve.

Detecting a signal in the presence noise is an old and well-studied problem, with a variety of fundamental techniques (or detectors) contained in the literature. However, the application of these various detectors in the special case of transit identification has not been thoroughly explored. While there have been many papers on planetary transit searches published in the past few years, these have primarily been focused on publishing results. The descriptions of the detectors used therein to isolate transit events have been condensed, neglecting a full description of the nuances that arise in this astronomical context. There are only a few exceptions. Kay (1998) states that a matched filter detector is the best in the case of Gaussian noise (white or colored, if pre-whitened), but this is not necessarily going to be the case in all circumstances, especially considering all of the processing that is required to prepare data for transit searches.

A literature search reveals a wide variety of detectors that can be used to identify transits in light curves. The first paper that attempts to deal with the topic of numerical methods for identifying transits is that of Jenkins et al. (1996). It discusses extensively the use of a matched filter detector in an attempt to identify transits in the particularly complicated case of the eclipsing binary CM Draconis. In their studies, Borucki et al. (2001) and Gilliland et al. (2000) used a slight variation on this same technique. In a further attempt to deal with the intricacies of CM Draconis, Doyle et al. (2000) developed a different detector. It is also labeled a matched filter approach, but it is fundamentally different from those used by other groups. To prevent confusion, this detector will hereafter be distinguished as Deeg's approach. Defaÿ et al. (2001) describes a detector based on Bayesian statistics that not only finds transits, but also determines the best-fit shape of the transit. Kovács et al. (2002) devises a box-fitting algorithm (BLS), which is based on direct least squares fits of step functions to the data. This is the only article that attempted to compare existing detectors. Among the detectors used in their comparison - which mostly included ones that were admittedly not designed for the identification of periodic events with short durations - was the Bayesian detector from Defaÿ et al. (2001), which did not fare favorably. Their article did not, however, include the matched filter approach in the analysis, nor were their comparisons completely rigorous, as they involved only a single simulated light curve.

2.1 The matched filter approach

The matched filter approach is one of the fundamental tools used in signal processing. According to Kay (1998), this is the optimal detector for a known signal with white Gaussian noise (WGN). Its conceptual basis is a calculation of the probability that a set of observations is the result of WGN or the result of an underlying signal Sn plus WGN. The test statistic is formed by taking the ratio of the noise probability and the signal + noise probability, which is known as the likelihood ratio. Taking the natural logarithm of this ratio converts the product of the probabilities into a summation and cancels out the exponentials from the Gaussian probability density functions. After shuttling some constants around, the basic formulation of its test statistic T becomes (see Kay 1998 for a full derivation):

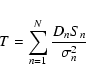\begin{displaymath}T = \sum_{n=1}^{N}\frac{D_{n}S_{n}}{\sigma_{n}^{2}} \end{displaymath} (1)

where D are the observed magnitudes, S is the test signal, $\sigma_{n}$is the S/N for each observation, and N is the number of observations in the light curve. S represents only a single set of test parameters, so in order to search for any transit in the observations, a S must be repeatedly modified so that parameter space can be covered. A test statistic is then generated for each test S, with the highest value of the test statistics corresponding to the most likely set of test parameters.

Implementation of the matched filter approach for transit identification can be significantly more complex than the basic formulation of the matched filter. This becomes readily apparent in the case of CM Draconis. First of all, the binary nature of the system not only affects the light curve with its regular eclipses, but also severely complicates the pattern of transits of any planet which might be present (Jenkins et al. 1996). Secondly, the data are taken at several different telescopes, each with its own CCD camera - or even just two-star photometers in one case - meaning that the quality of the data will vary systematically (Deeg et al. 1998), further muddling time series. Thirdly, all of the good comparison stars in the field were significantly bluer than CM Draconis, which resulted in residual nightly extinction variations (Doyle et al. 2000). Clearly, a simple matched filter approach is not sufficient for this circumstance. Jenkins et al. (1996), cleaned the data to a high degree by subtracting model eclipses. However, this still left the problem with the residual nightly extinction variation, which led the same group to develop another detector.

2.2 Deeg's approach

Deeg's approach is also based on the idea of comparing the data with a series of test signals spanning parameter space. It was specifically designed for the complex circumstances found in a data set of several years of observations of CM Draconis. It differs fundamentally from the matched filter approach described above in that it includes a time-based weighting.

In order to generate their test statistic, Doyle et al. (2000) generated a test signal with transits included (the with-planet test signal). They subtracted this with-planet test signal from the light curve for each individual night of observations and fit a parabola to what remained. Then they fit a parabola to each individual night of observations, which is intended to model the residual nightly extinction variation. These fits are then compared to the original data and the residuals determined. From these residuals, the test statistic is calculated:

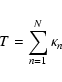\begin{displaymath}T = \sum_{n=1}^{N}\kappa_{n} \end{displaymath} (2)

where

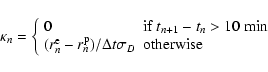
\begin{displaymath}\kappa_{n} = \left\{ \begin{array}{ll} 0 & \mbox{if $t_{n+1}-... ..._{n})/\Delta t\sigma_{D} & \mbox{otherwise} \end{array}\right. \end{displaymath}

with

\begin{displaymath}\Delta t = (t_{n+1}-t_{n}), \end{displaymath}


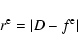
\begin{displaymath}r^{\rm e} = \vert D - f^{\rm e}\vert\end{displaymath}

and

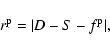
\begin{displaymath}r^{\rm p} = \vert D - S - f^{\rm p}\vert,\end{displaymath}

where $f^{\rm e}$ is the best-fit parabola in the no-planet case, $f^{\rm p}$is the best-fit parabola in the with-planet case, $\sigma_{D}$ is the noise level for the night analyzed, and tn is the time of the observation. The inclusion of time in this detector is unique, effectively weighting each element of the test statistic by the time between consecutive observations. If this $\delta t$ is too long, however, the points are neglected, as these regions of the light curve correspond to "holes'' in the data. According to Doyle et al. (2000), this time-based weighting was necessary to account for the difference in time increments of the observations from different telescopes.

2.3 Bayesian approach

The Bayesian approach described by Defaÿ et al. (2001) is based on a different statistical philosophy than the previously mentioned techniques. In a nutshell, it estimates an unknown parameter through the maximization of a likelihood function, invoking as much prior information as possible in order to improve the estimation.

The primary parameter that Defaÿ et al. fit is the period of the signal to be detected. They assume that the noise was WGN and then represented the signal as an unknown Fourier series. By finding the most likely period of the signal, the coefficients of the Fourier series can then be determined, fitting the actual shape of the transit. The likelihood function that they derive, to be maximized for frequency corresponding to the period of the signal, is

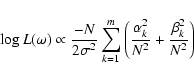\begin{displaymath}\log L(\omega) \propto \frac{-N}{2\sigma^{2}} \sum_{k=1}^{m}... ...ac{\alpha_{k}^{2}}{N^{2}} +\frac{\beta_{k}^{2}}{N^{2}}\right) \end{displaymath} (3)

where

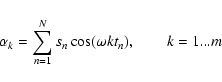\begin{displaymath}\alpha_{k} = \sum_{n=1}^{N}s_{n}\cos(\omega kt_{n}),\qquad k = 1...m \end{displaymath} (4)


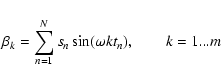\begin{displaymath}\beta_{k} = \sum_{n=1}^{N}s_{n}\sin(\omega kt_{n}),\qquad k = 1...m \end{displaymath} (5)

sn is the nth point in the light curve, tn is its corresponding time, and $\omega$ is the frequency. In theory, $m \rightarrow \infty$ is necessary to fit the transit shape properly. However, the authors truncate the summations of $\alpha_{k}$ and $\beta_{k}$ at m = 7 to reduce the considerable computational load of this approach, claiming that this can be safely done without loss of precision. After the equation has been maximized and the most likely frequency determined, the shape of the transit can be reconstructed:

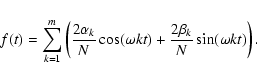\begin{displaymath}f(t) = \sum_{k=1}^{m}\left(\frac{2\alpha _{k}}{N}\cos(\omega kt)+\frac{2\beta _{k}}{N}\sin(\omega kt)\right). \end{displaymath} (6)

It is important to remember that this implementation of the detector works only for data without "holes'', although it could be modified for the case of unevenly sampled data.

2.4 The box-fitting technique

The box-fitting method described by Kovács et al. (2002) is essentially a $\chi^{2}$ fit of a square-well transit model to the observations. Through minimization, they are able to remove the depth of the transit as a free parameter, reducing the computational load. The expression to be minimized for a given n1 and n2 is

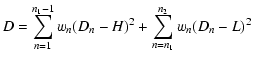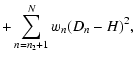$\displaystyle D = \sum_{n=1}^{n_{1}-1}w_{n}(D_{n}-H)^{2}+\sum_{n=n_{1}}^{n_{2}}w_{n}(D_{n}-L)^{2}$$\displaystyle +\sum_{n=n_{2}+1}^{N}w_{n}(D_{n}-H)^{2},$     (7)

where $w_{n} = \sigma_{n}^{-2}[\sum_{m=0}^{N-1}\sigma_{m}^{-2}]^{-1}$ is the normalized weight of each data point, L is the signal during transit (between n=n1 and n=n2), and H is the signal outside the transits. The authors then make the assumption that the average of the D is zero. This allows them to reduce the number of parameters from five (P0, the period of the repeating transit, q, the fractional transit length, L, H, and t0, the epoch of the transit) to four with the substitution of H = -Lq/(1-q). This is accurate provided that q is small. This substitution allows Lto be parameterized as $\frac{s}{r}$ and H as $-\frac{s}{1-r}$, where $s=\sum_{n=n_{1}}^{n_{2}}w_{n}D_{n}$ and $r=\sum_{n=n_{1}}^{n_{2}}w_{n}$. The expression to be minimized then becomes

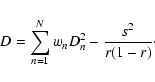\begin{displaymath}D=\sum_{n=1}^{N}w_{n}D_{n}^{2} - \frac{s^{2}}{r(1-r)}\cdot \end{displaymath} (8)

This particular form of the equation is useful. Not only does the first term not depend on n1 and n2, allowing it to be dropped, but neither of the terms include the depth of the transit, creating a test statistic that is now independent of this free parameter:

\begin{displaymath}T = {\rm max}\left\{\left[\frac{s^{2}({n_1},{n_2})}{r({n_1},{n_2})-[1-r({n_1},{n_2})]}\right]\right\}^{\frac{1}{2}}\cdot \end{displaymath} (9)


  \begin{figure} \par\includegraphics[width=12.4cm,clip]{gausscomp.ps} \end{figure} Figure 1: This figure shows the comparison between the distribution of the observations used to generate the virtual light curves (dashed line) and a Gaussian distribution (solid line). Notice the excess where the normalized distance from the center of the distribution is greater than 1.1. Despite the fact that it looks large, it is actually due to just 10 out of the 104 observations.

2.5 Correlation

The correlation is a very basic statistical tool used to measure how well two samples resemble each other. It is not included here as a serious transit identification method, but instead primarily as a point of reference. Since it is not designed for transit identification, it can be used as a benchmark to measure the effectiveness of the statistical philosophies behind the various detectors. The textbook definition of the coefficient of linear correlation is

\begin{displaymath}T = \frac{\sum_{n=0}^{N-1}(D_{n}-\bar{D})(S_{n}-\bar{S})} {[... ...{D})^{2}\sum_{n=0}^{N-1} (S_{n}-\bar{S})^{2}]^{\frac{1}{2}}}, \end{displaymath} (10)

where $\bar{D}$ and $\bar{S}$ are the averages of the light curve and the expected signal, respectively.

2.6 Aigrain's approach

Aigrain & Favata (2002) take the same Bayesian philosophies used by Defaÿ et al. (2001) and extend them to assume square well transits. Ultimately, the mathematical basis proves to be very similar to the matched filter, different primarily in the way that parameter space is explored - the matched filter makes cuts across parameter space, while the Bayesian ultimately integrates over parameter space. While this is interesting in and of itself, the limited number of parameters explored in the simulations performed in this analysis would not be sufficient to examine the effect of this difference. For this reason, no attempt to include this approach in this paper is made.

3 Comparison method

In order to compare the various transit identification techniques, virtual light curves should be generated in as realistic a manner as possible and the most influential parameters must be identified. In addition, a fair method to compare the results of the different techniques must be applied in order to form a definitive conclusion.

Several parameters are needed to characterize the signal caused by a transiting ESP and more to characterize the observations of one. The transit itself can be defined by a few physical parameters: depth, width, time of the first observed transit and period. Including the observations requires more: the S/N of the observations, the rate of the observations and the time coverage of the observations. This proves to be an unwieldy number of parameters to simulate, so the period is fixed at 3 days and the width at 3 hours. Additionally, the time of the first transit is also held constant, as it proved not to make any difference. The depth of the transit and the S/N are combined into one parameter, the normalized depth (d). The period and the time coverage are also combined into one parameter, the number of transits observed ( $N_{\rm tr}$). This leaves only the rate of observations ( $r_{{\rm obs}}$). By varying these last three parameters, parameter space is covered to a sufficient extent for an evaluation of detector performance.

The standard technique to construct synthetic light curves is to use a random number generator that produces WGN for the virtual observations. This is an assumption that does not necessarily represent the properties of the noise in real data. In order to avoid this, the virtual light curves are created by drawing individual observations (as opposed to short sequences of consecutive observations) randomly from a set of more than 104 real observations. This set is derived from observations of NGC 6791 by Bruntt et al. (in preparation), consisting of data from 17 stars, each non-variable, from a small region of the main sequence, and with variances between $4.95\times10^{-5}$ and $6.10\times10^{-5}$. The light curve for each star was $\sigma $-clipped, first to remove extreme outliers and again to remove more intermediate outliers that ultimately reduced the furthest outlier to slightly more than $4\sigma$. After this, each light curve was individually normalized to create the combined set.

It is important to determine how closely this set of observations matches WGN in order to understand how globally applicable the results from this article can be. One way of doing this is to compare its right-tail probabilities with that of the best-fit Gaussian. As the values in the set are already normalized, a direct comparison to the complementary cumulative distribution function ( $\frac{1}{2}-\frac{1}{2}{\rm erf} \left(\frac{x}{\sqrt{2}}\right)$, where ${\rm erf}(x)$ is the error function) is sufficient. As can be seen in Fig. 1, there is an excess far out in the wings of the distribution, which can be explained by approximately 10 outlying observations. This is a very small percentage of the total, meaning that the distribution strongly resembles the Gaussian without being identical, which is typical of real observations.

While the study of individual light curves might be instructive on a case by case basis, a Monte Carlo simulation is truly needed to compare the different detectors reliably. For each set of transit parameters, 104 light curves are generated. The temporal spacing of the simulated observations is allowed to vary up to 10% of the average spacing, with no large gaps representing daytime included - although in principle this would only affect the current implementation of the Bayesian approach.


 

 
Table 1: Probabilities of detection for a false alarm rate of 1% for various transit parameters and detectors. $N_{\rm tr}$ is the number of transit, $r_{{\rm obs}}$ is the rate of observations in observations per hour and d is the depth of the transit in normalized magnitude - effectively the S/N of the observations.
Transit parameters Probability of Detection
$N_{\rm tr}$ $r_{{\rm obs}}$ d BLS Bayesian Correlation Matched Filter Deeg's
3 5 0.10 0.0117 0.0105 0.0110 0.0131 0.0122
3 5 0.25 0.0186 0.0155 0.0341 0.0434 0.0380
3 5 0.50 0.1393 0.0500 0.3920 0.4590 0.3617
3 10 0.10 0.0109 0.0111 0.0160 0.0175 0.0156
3 10 0.25 0.0359 0.0244 0.1105 0.1319 0.0887
3 10 0.50 0.5607 0.1445 0.8454 0.8867 0.8014
6 5 0.10 0.0110 0.0111 0.0158 0.0181 0.0152
6 5 0.25 0.0224 0.0179 0.1148 0.1451 0.1084
6 5 0.50 0.4846 0.1136 0.8574 0.8996 0.8193
6 10 0.10 0.0123 0.0123 0.0251 0.0294 0.0225
6 10 0.25 0.0974 0.0339 0.3882 0.4406 0.3052
6 10 0.50 0.9528 0.4460 0.9986 0.9993 0.9951
10 5 0.10 0.0101 0.0113 0.0202 0.0232 0.0184
10 5 0.25 0.0434 0.0216 0.3006 0.3392 0.2311
10 5 0.50 0.8064 0.3017 0.9911 0.9951 0.9863
10 10 0.10 0.0122 0.0118 0.0391 0.0478 0.0342
10 10 0.25 0.2234 0.0595 0.7325 0.7898 0.6319
10 10 0.50 0.9983 0.8371 1.0000 1.0000 1.0000


In order to compare the transit identification algorithms, each of the randomly generated light curves are copied, then transits are added to the copy. Each of the detectors are then applied to both copies of the light curve, scanning phase space for transits identical to those added on, generating a test statistic for each phase. The peak of these test statistics corresponds to the most likely phase of the transits. In the case of the with-transit light curves, this is usually the inserted transits, depending on the response of the detector to the transits included. For the light curves without transits included, the peak is the strongest false alarm - a false alarm being defined as a chance occurrence of noise that to a greater or lesser extent resembles the sought-after signal. These peaks can then be gathered and the resulting distributions analyzed to determine how well the algorithms identify transits. It should be noted that there are instances when a given detector does not find transits even though they are present. These instances will be increasingly more common as the transit signals become weaker. This means that the with-transit distributions increasingly resemble the without as the transit signals weaken.

There are two standard ways of comparing the performance of detectors. One is through an examination of Receiver Operating Curves (ROCs), which plot the chance of detection against the chance of false alarm. The better the detector is, the higher it lies in this type of diagram. The worst case scenario - simple guessing - is represented by a straight line with unity slope. These diagrams are easily made with a simple calculation from the with-transits and without-transit distributions for individual detectors and sets of transit parameters. Another way to compare detectors is to calculate the probability of detection at a given probability of false alarm. This is done simply by ranking the without-transit distributions, determining the detection thresholds corresponding to the desired false alarm probabilities (FAPs), and calculating the portions of the with-transit distributions that exceeds these values.


 

 
Table 2: This table contains the results from verification simulation, which used the input parameters (3,3,0.5). The first column lists the detectors. The second column lists the probabilities of detection from Table 1 for the same input parameters. The third column liststhe probability of detection based on 106 iterations with a FAP of 1%, while the accompanying errors are the standard deviation calculates from the 100 subsets of 104 iterations in the total sample. The last two columns show the probabilities of detection with false alarm probabilities of 10-3 and 10-4 respectively.
  Probabilities False Alarm Probability
Detector from Table 1 $10^{-2} \pm {\rm err}$ 10-3 10-4
BLS 0.1393 $0.1478 \pm 0.0069$ 0.0519 0.0155
Bayesian 0.0500 $0.0505 \pm 0.0034$ 0.0091 0.0016
Correlation 0.3920 $0.3842 \pm 0.0128$ 0.1786 0.0670
Matched filter 0.4590 $0.4517 \pm 0.0123$ 0.2313 0.0943
Deeg's 0.3617 $0.3804 \pm 0.0114$ 0.1783 0.0713


When using Monte Carlo simulations, more events always yield more reliable results. Unfortunately, some of the algorithms - in particular the Bayesian - are computationally intensive. Despite the use of a dedicated machine with $8\times1.9$ GHz Athlon processors working in parallel, the simulations took several weeks to run in total, despite holding several of the key parameters (period and duration) constant. The FAPs that can be reliably estimated are restricted by the number of events used in the Monte Carlo simulations. Reducing the FAP produces a broader distribution in the results for a fixed number of events, which could blur the distinction between the detectors. To evaluate detector performance, it is necessary to use as low a FAP as possible because the distributions are not identical, meaning that one detector could be better than another at a relatively high FAP but worse at a lower one. A balance between these two needs is required. As 104 events were used for the simulations, a FAP of 1% is suitable, providing a low enough FAP for a good comparison while keeping the distributions narrow enough to evaluate detector performance. In order to ascertain the results of this analysis, a single set of parameters is simulated with 106 events, allowing both for the widths of the distributions to be estimated and for lower false alarm probabilities to be examined. This will help to verify that the relative performance of the different detectors remains more or less constant.


  \begin{figure} \par\includegraphics[width=12cm,clip]{rocs.ps} \end{figure} Figure 2: The plot on the left shows the Receiver Operating Curves for all five detectors used in the simulations for the fixed set of parameters $(N_{\rm tr} = 3, r_{{\rm obs}} = 5, d = 0.5)$. The curved solid line is the matched filter, the long dashed line is the correlation, the dotted line is Deeg's approach, the short dashed line is the BLS and the dot-dashed line is the Bayesian. The straight solid line shows the limit that corresponds to random guessing. The plot on the right shows the same diagram for the matched filter approach and different transit parameters. In the format $(N_{\rm tr}, r_{{\rm obs}},d)$, the curved solid line is (6,5,0.5), the long dashed line is (3,5,0.5), the dotted line is (6,5,0.25), the short dashed line is (3,5,0.25) and the dot-dashed line is (3,5,0.1). The lines from the other sets of input parameters tested would be nearly indiscernibly crowded into the upper left-hand corner of the diagram, as they represent stronger transit signals.


  \begin{figure} \par\includegraphics[width=12.3cm,clip]{Pdstraight.ps} \end{figure} Figure 3: A plot of $\ln(1-(\ln(1-P_{{\rm D}}))$ against $N_{{\rm obs}} \times \sigma ^{2}$, where $P_{{\rm D}}$ is the probability of detection for a false alarm rate of 10-2, $N_{{\rm obs}}$ is the number of observations while the planet is in transit and $\sigma $ is the depth of the transit observed. The values in this plot are taken from the matched filter approach column in Table 1. The point corresponding to (10,10,0.5) is missing because, due to the limited number of events in the simulation, its $P_{{\rm D}}$ equals one and is therefore undefined in the function used. The asterisks show the actual values from Table 1, while the dashed line (with a slope of 0.1668) is the best fit straight line to these values.

4 Results

The simulations were performed and the results are shown in Table 1, which contains the input parameters (the number of transits, the rate of observations, and the depth of the transits) and the probabilities of detection for the different detectors described above. They demonstrate clearly that the matched filter is the superior detector. It is followed unexpectedly by the simple correlation and then Deeg's approach. The BLS and the Bayesian are significantly worse, despite the fact that these are the only two detectors that have had papers in the astronomical literature on them specifically. Table 2 demonstrates that the results in Table 1 are reliable, as the scatter of the distributions derived is less than the difference between the detectors and that the rank of the detectors does not change as the FAP is reduced. A pair of ROCs is given in Fig. 2. The left panel shows the response for different detectors to a single set of input parameters (3,5,0.5) and the right panel shows the response of a single detector (the matched filter approach) to different sets of input parameters.

The response of these different detectors to changes in parameters can also provide insight into their performance. From inspection, or just from a basic understanding of statistics, it seems likely that the significant parameters that govern the detectability of a transit are the number of observations of the planet during transit and the S/N of those observations. The number of observations during transit in these simulations is proportional to the rate of observations and the number of transits observed. The S/N is related to the depth of the transit in the simulations performed, as one can equate changing the depth of the transit to changing the S/N of the observations. These two fundamental parameters are also related in another way, as the S/N is inversely proportional to the square root of the exposure time.

In order to determine if there might be some definable relationship between these fundamental parameters and the probability of detection, an understanding of the latter must be obtained. If the with-transit distribution is Gaussian, then the probability of detection will be equal to the integral of this Gaussian from the point of the chosen false alarm probability to infinity. This has no simple, analytical solution, but it is related to the exponential, which provides a starting point for the empirical investigation. Figure 3 shows a plot of the number of observations during transit times the square of the S/N (depth) versus $\ln(1-(\ln(1-P_{{\rm D}}))$, where $P_{{\rm D}}$ is the probability of detection. While the fit is not perfect, it does strongly suggest that the probability of detection can be well-estimated from fundamental parameters. This is particularly true at moderate to high probabilities, which is the region of interest. Hopefully this will also mean that an estimation like this is possible for the false alarm probability, although that analysis is beyond the scope of the simulations performed here, as it would require several orders of magnitude more iterations.

5 Conclusion

A Monte Carlo simulation using randomly generated light curves drawn from a set of real data to compare the effectiveness of the different planetary transit identification algorithms has been performed. Of the methods tested, which included the matched filter approach, the linear correlation, the Bayesian of Defaÿ et al. (2001), the BLS of Kovács et al. (2002) and modified matched filter detector of Doyle et al. (2000), the matched filter demonstrated the best performance, while the BLS and the Bayesian both performed poorly by comparison.

An important thing to consider before dismissing the BLS and the Bayesian is that both of these detectors searched not only for the best phase but also for the best period, while the other detectors searched only for the best period in these simulations. This extra free parameter could certainly affect the results of the Monte Carlo simulations, even though the period search was strongly limited to a region close to the known period. Additionally, neither one of these techniques has the depth of the transit per se as a free parameter. However, the true advantage of this was not seen in the simulations in this paper, as only the known depth of the transit was searched for. This means that the approaches that had depth as a free parameter (the matched filter, the linear correlation, and Deeg's approach) were not entirely accurately represented, as they would otherwise have required more statistical tests, which would increase the overall level of the false alarms, reducing the detection probability at a FAP of 1%. Perhaps it is not surprising, then, that these three approaches ranked as the three best. As with Aigrain's approach, further analysis covering more parameters might be necessary for a completely accurate comparison.

The BLS, as stated in its description in Sect. 2.4, makes use of a $\chi^{2}$fit. Interestingly, an expectation of the relative performance of a $\chi^{2}$ fit and the matched filter approach can inferred mathematically. They are in fact closely related, the $\chi^{2}$ fit being one type of purely statistical test and the likelihood ratio from which the matched filter is derived being another. It becomes evident when one expands the basic formulation for the $\chi^{2}$

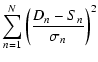                            $\displaystyle \chi^{2}$ = $\displaystyle \sum_{n=1}^{N}\left(\frac{D_{n}-S_{n}}{\sigma_{n}}\right)^{2}$  
  = $\displaystyle \sum_{n=1}^{N}\left[\left(\frac{D_{n}}{\sigma_{n}}\right)^{2}-2\l... ...}S_{n}}{\sigma_{n}}^{2}\right)+\left(\frac{S_{n}}{\sigma_{n}}\right)^{2}\right]$ (11)

and compares it term by term with the matched filter. The last term is strictly defined and can therefore be neglected, as is done in the derivation of the matched filter from the likelihood ratio, where the same term appears. The middle term is actually proportional to the matched filter itself. This means that the only significant difference that remains between the two detectors is the first term. This term has no dependence on the test signal and therefore does not improve the ability of the detector to discern the signal. On average, it will be approximately equal to N, but there will be scatter around this value. This scatter is ultimately an extra noise source. Therefore, the best modification one can make to the $\chi^{2}$ fit is to remove this extra source of noise, leaving it equivalent to the matched filter. This is exactly what Kovács et al. do in the derivation of their test statistic. This means, in effect, the only mathematical difference between the matched filter and the BLS is that the BLS has the depth removed as a free parameter. Further simulations are required to determine if this actually helps, however, as the computational load of the BLS and the matched filter are quite similar, even including depth as a free parameter.

The Bayesian approach exhibits several qualities that could affect its performance, related to the fact that it performs a Fourier fit to the shape of the transit. Defaÿ et al. (2001) state that this is an improvement over the matched filter approaches offered by Jenkins et al. (1996) and Doyle et al. (2000). However, according to Kay (1998), the use of known information to improve the chance of making the proper decision between hypotheses is one of the central ideas of the Bayesian philosophy. As the shape of any planetary transit can be represented very well by square wells of different depths and widths, it would seem that this information could be used to improve the chance of making an identification. Furthermore, this algorithm limits the number of frequencies used to make the fit to m=7, which the authors claim is sufficient. However, when using a multi-frequency Fourier fit, it is crucial to have enough frequencies to fit the ultimate transit shape accurately. Otherwise, signal energy will be lost, hurting the performance of the detector.

Lastly, in addition to the comparison of the detectors, there appears to be something of an empirical relation between the fundamental parameters (the number of observations during transit and the S/N of those observations) and the probability of detection at a fixed false alarm probability. The realization that transit signal energy is defined by the number of observations during transit times the square of the S/N of those observations is an important result itself, one that could be used to expand free parameter space later simulations without drastically increasing computational load.

Acknowledgements
Many thanks go to Jon Jenkins at SETI Institute for the great improvement he coaxed out of this paper with his patience and thorough refereeing. I would like to thank the Danish Natural Sciences Research Council for financial support. And finally I would like to thank Hans Kjeldsen and Jørgen Christiansen-Dalsgaard for all the support they have provided me over the past two years.

References


Copyright ESO 2003