A&A 402, 949-962 (2003)
DOI: 10.1051/0004-6361:20030302
C. Zanni 1,2 - G. Bodo2 - P. Rossi 2 - S. Massaglia1 - A. Durbala 1,2,3 - A. Ferrari 1
1 - Dipartimento di Fisica Generale dell'Università,
Via Pietro Giuria 1, 10125 Torino, Italy
2 -
INAF - Osservatorio Astronomico di Torino, Strada dell'Osservatorio
20, 10025 Pino Torinese, Italy
3 -
Universitatea din Bucuresti, Facultatea de fizica atomica si nucleara,
Bucuresti-Magurele,
PO Box MG-11, Romania, Italy
Received 3 December 2002 / Accepted 21 February 2003
Abstract
X-ray observations of extragalactic radiosources show strong evidences
of interaction between the radio emitting plasma and the X-ray
emitting ambient gas. In this paper we perform a detailed
study
of this interaction by numerical simulations. We study the propagation
of an axisymmetric supersonic jet in an isothermal King atmosphere and
we analyze the evolution of the resulting X-ray properties and their
dependence on the jet physical parameters. We show the existence of
two distinct and observationally subsequent different regimes of interaction,
with strong and weak shocks. In the first case shells of enhanced
X-ray emission are to be expected, while in the second case we expect
deficit of X-ray emission coincident with the cocoon. By a comparison
between analytical models and the results of our numerical
simulations, we discuss the dependence of the transition between these
two regimes on the jet parameters and we find that the mean controlling
quantity results to be the jet kinetic power. We then discuss how
the observed jets can be used to constrain the jet properties.
Key words: X-rays: galaxies: clusters - galaxies: jets - hydrodynamics
X-ray observations of extragalactic radio sources have revealed strong evidences of interaction between the radio emitting plasma and the X-ray emitting gas in the ambient medium. The observation of Cygnus A with the ROSAT HRI (High Resolution Imager) by Carilli et al. (1994) and with the Chandra X-ray Observatory (Smith et al. 2002) showed deficits of X-ray emission in the cluster gas spatially coincident with the radio lobes. Observations of the Perseus cluster by Böhringer et al. (1993), also with ROSAT, and by Fabian et al. (2000) with the Chandra X-ray Observatory showed that the cluster emitting gas was displaced by the radio lobes of the source NGC 1275. A similar behavior has been observed in the Hydra A cluster, hosting the radio source 3C 218, with the Chandra X-ray Observatory by McNamara et al. (2000) (see also Nulsen et al. 2002), and in Abell 2052 that shows regions devoid of X-ray emission coincident with the radio lobes of 3C 217 (Blanton et al. 2001). Other clear examples of the interaction between radio lobes and the surrounding cluster gas are given by A 4059 (Heinz et al. 2002, Chandra) and A 2199 (Owen & Eilek 1998, ROSAT). Disturbances by a radio source are also found in the gas halo of some giant elliptical galaxies such as M 87 (Böhringer et al. 1995, ROSAT) and M 84 (Finoguenov & Jones 2001, Chandra).
On the other hand, theoretical models predict that jets in
radiogalaxies inflate overpressured cocoons that displace and compress
the ambient gas and the effects of such interaction could indeed
expected to be the formation of cavities and shells in the X-ray
emission, as shown by observations. A simple one-dimensional model of
this interaction has been presented by Begelman & Cioffi (1989). More
detailed and realistic models require the use of numerical simulations.
In this context, Clarke et al. (1997) carried out
calculations of the jet propagation in a King atmosphere obtaining
simulated X-ray images to compare with ROSAT data on Cygnus A. They
demonstrated that a deficit in the X-ray brightness is indeed shown in
the simulation results and found agreement between simulations and
observations for moderate Mach number of the jet (![]() ).
A similar scenario is depicted by the numerical simulations of Rizza et al. (2000)
that showed the interaction and disruption of a jet inside a cooling
flow cluster. More recently
Reynolds et al. (2001) have pointed out that cocoons start being strongly
overpressured, but, during their evolution, their pressure decreases,
and they then become essentially in pressure equilibrium with the
ambient or even underpressured. During this evolution, therefore, the
shock driven in the external medium is strong at the beginning and
becomes very weak at the end. Reynolds et al. (2001) call this last phase "sonic
boom''. The need for weak shocks comes from the observations of cool rims
surrounding some of the X-ray cavities (see A 2052, Hydra A, Perseus A) that rule
out the possibility of strong shocks driven by the expanding cocoon.
To explain these observations several analytical (Churazov et al. 2000;
Soker et al. 2002) and numerical (Churazov et al. 2001; Brighenti &
Mathews 2002; Quilis et al. 2001) models of "bubbles'' of hot plasma expanding
subsonically in the ambient medium have been studied. If these bubbles
are buoyant they can also explain the presence of deficits of X-ray
emission far from the radio lobes as observed in Perseus A.
On the other hand, Heinz et al. (1998) and Alexander (2002) have studied self-similar
solutions of simplified analytical models of overpressured cocoons expanding in
a stratified medium in order to explain the observed features.
).
A similar scenario is depicted by the numerical simulations of Rizza et al. (2000)
that showed the interaction and disruption of a jet inside a cooling
flow cluster. More recently
Reynolds et al. (2001) have pointed out that cocoons start being strongly
overpressured, but, during their evolution, their pressure decreases,
and they then become essentially in pressure equilibrium with the
ambient or even underpressured. During this evolution, therefore, the
shock driven in the external medium is strong at the beginning and
becomes very weak at the end. Reynolds et al. (2001) call this last phase "sonic
boom''. The need for weak shocks comes from the observations of cool rims
surrounding some of the X-ray cavities (see A 2052, Hydra A, Perseus A) that rule
out the possibility of strong shocks driven by the expanding cocoon.
To explain these observations several analytical (Churazov et al. 2000;
Soker et al. 2002) and numerical (Churazov et al. 2001; Brighenti &
Mathews 2002; Quilis et al. 2001) models of "bubbles'' of hot plasma expanding
subsonically in the ambient medium have been studied. If these bubbles
are buoyant they can also explain the presence of deficits of X-ray
emission far from the radio lobes as observed in Perseus A.
On the other hand, Heinz et al. (1998) and Alexander (2002) have studied self-similar
solutions of simplified analytical models of overpressured cocoons expanding in
a stratified medium in order to explain the observed features.
In this paper we analyze in detail, by using numerical simulations, the evolution of the X-ray properties of expanding cocoons and their dependence on the jet properties. The jets are characterized by their Mach number and their density ratio with the ambient medium density; the parameter plane is widely covered in order to consider a wide range of jet powers. We confirm the results presented by Reynolds et al. (2001) on the existence of two distinct and observationally different subsequent regimes of interaction, with strong or weak shocks but we are able to determine how and when the transition between these two regimes occurs, depending on the jet parameters. These results, on the other hand, show how the X-ray properties of cocoons could possibly be used as diagnostic for the jet characteristics.
The plan of the paper is the following: in Sect. 2 we describe the model, the basic equations and the initial conditions, in Sect. 3 we discuss the X-ray morphologies resulting from the simulations, in Sect. 4 we discuss the heating of the external material compressed by the expanding cocoon and the consequent changes in the X-ray emission properties, in Sect. 5 we discuss the physics of the cocoon expansion that leads to the interpretation of the different X-ray morphologies and in Sect. 6 we discuss the astrophysical relevance of our results, finally a summary is presented in Sect. 7.
We solve numerically the hydrodynamic equations for a supersonic
jet, in cylindrical (axial) symmetry in the coordinates (r,z)continuously injected into a gravitationally stratified (but not
self-gravitating) medium
The system of Eqs. (1) has been solved
numerically employing a PPM (Piecewise Parabolic Method) hydrocode (Woodward
& Colella 1984).
The integration domain has a size
![]() where
where
![]() ,
where a is
the core radius, defined below, and
has been divided in
,
where a is
the core radius, defined below, and
has been divided in
![]() grid points. The axis of the jet is
along the left boundary of the domain (r=0), where we have imposed
symmetric boundary conditions for
grid points. The axis of the jet is
along the left boundary of the domain (r=0), where we have imposed
symmetric boundary conditions for
![]() and
antisymmetric conditions for vr. Reflective boundary conditions are
also imposed on the boundary of injection of the jet (z=0) outside its
radius in order to reproduce a bipolar flow and to avoid spurious inflow
effects.
Free outflow is set on the
remaining boundaries by imposing a null gradient for each variable (
and
antisymmetric conditions for vr. Reflective boundary conditions are
also imposed on the boundary of injection of the jet (z=0) outside its
radius in order to reproduce a bipolar flow and to avoid spurious inflow
effects.
Free outflow is set on the
remaining boundaries by imposing a null gradient for each variable (
![]() ).
).
The undisturbed ambient medium is assumed stratified in a spherically
symmetric gravitational well, according to a classical isothermal King
model:
![\begin{displaymath}\rho_{\rm ext}(R)=\frac{\rho(0)}{\left[1+(R/a)^2 \right]^{3\beta/2}} \;,
\end{displaymath}](/articles/aa/full/2003/18/aah4150/img37.gif) |
(2) |
A (cylindrical) jet is injected from the bottom
boundary of the integration domain, in pressure balance with the ambient. The
initial jet velocity profile has the form
![\begin{displaymath}v_z(r)=
\frac{\displaystyle v_{\rm j}}{\displaystyle \cosh\left[(20 \ r/a)^m\right]}
\end{displaymath}](/articles/aa/full/2003/18/aah4150/img40.gif) |
(3) |
![\begin{displaymath}\rho(r,z)=
\frac {\displaystyle \rho_{\rm j}-\rho_{\rm ext}(R...
...laystyle \cosh\left[(w \
20 \ r/a)^n\right]}+\rho_{\rm ext}(R)
\end{displaymath}](/articles/aa/full/2003/18/aah4150/img41.gif) |
(4) |
Measuring lengths in units of the core radius a, velocities in units of the
adiabatic sound speed
![]() in the undisturbed external medium and the density in
units of the ambient central density
in the undisturbed external medium and the density in
units of the ambient central density ![]() ,
our main parameters are the
Mach number
,
our main parameters are the
Mach number
![]() and the density ratio
and the density ratio
![]() .
Consistently the unit for the kinetic power is
.
Consistently the unit for the kinetic power is
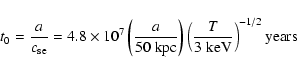 |
(6) |
| M | Lj/Lk |
|
|
| 10 | 0.1 | 102 | 1.38 |
| 60 | 0.001 |
|
1.22 |
| 60 | 0.01 |
|
0.49 |
| 60 | 0.1 |
|
0.15 |
| 120 | 0.001 |
|
0.76 |
| 120 | 0.01 |
|
0.25 |
| 120 | 0.1 |
|
0.07 |
The general structure of the interaction between a low density jet and the ambient medium is well known since the first simulations of Norman et al. (1982) (see also Massaglia et al. 1996 and Krause 2003). The flowing jet matter, slowed down by one or more terminal shocks, inflates a cocoon that compresses and drives shocks in the surrounding external medium. The compressed ambient material forms a shell surrounding the cocoon: the boundary between the shell and the cocoon is marked by a contact discontinuity, while the boundary between the shell and the undisturbed external medium is marked by a shock. We will call "extended cocoon'' the whole region interested in the interaction between the jet and the ambient medium. The "extended cocoon'' is then formed by the cocoon proper and by the surrounding shell. The cocoon, which is formed by the expanded jet material forms a cavity with very low density and high temperature, in which the X-ray emissivity is strongly depressed. On the other hand the external material in the shell has an enhanced emission due to its compression. In addition, depending on the external shock strength this material can be heated and its emission properties can then change.
In principle, we then expect three main features in the X-ray properties of the region of interaction between a jet and the ambient medium:
In Figs. 1-3 we show in the first
two columns simulated X-ray flux distribution
for the seven cases described in Table 1.
The figures are symmetrical with respect to the r and z axes.
The emissivity per frequency unit is computed with a Raymond-Smith
thermal spectrum code (see HEASARC Web Page) from the electron density
and temperature distribution obtained in our calculation.
The emissivity
![]() is then
integrated in the
is then
integrated in the
![]() band. The flux distribution
is calculated integrating the optically thin emissivity along the line of sight
band. The flux distribution
is calculated integrating the optically thin emissivity along the line of sight ![]() that is assumed perpendicular to the jet axis:
that is assumed perpendicular to the jet axis:
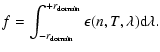 |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{H4150F2.ps}
\end{figure}](/articles/aa/full/2003/18/aah4150/Timg64.gif) |
Figure 2:
Simulated X-ray fluxes,
in logarithmic scale, in the 0.1-4 keV band for the M=60 cases. The rows
refer from top to bottom to the
|
| |
Figure 3:
Simulated X-ray fluxes,
in logarithmic scale, in the 0.1-4 keV band for the M=10, |
These figures show a sequence of morphologies starting from cases in
which a cavity is not present going to cases in which the cavity is
the dominant feature of the image. In particular, we see that for M
= 120 the brightness depression is evident only for the lighter case,
while for the M = 60 cases starts to be present for
![]() during its evolution and is very
evident during the whole evolution for
during its evolution and is very
evident during the whole evolution for
![]() .
For M = 10the cavity is dominant already for
.
For M = 10the cavity is dominant already for ![]() .
.
The presence or absence of the brightness
depression, as discussed by Clarke et al. (1997) depends on the
thickness of the shell. In fact, the line of sight that goes through
the cocoon region with very low emissivity crosses also the shell of enhanced
emissivity, and the observed flux is higher or lower than the undisturbed
profile depending on the interplay between the two effects. If the
shell is narrow, as a consequence of mass conservation, it will have
a high density, the emissivity will be greatly enhanced and will overcome
the decrease in the cocoon giving an observed brightness higher than the
undisturbed profile. Following Clarke et al. (1997), we can write the
ratio of the observed flux to the undisturbed one as
In Fig. 4 we show the
density distribution for the M = 60 cases: each row refers to a
different density ratio (
![]() from top to bottom)
and each column is for different times corresponding to cocoon lengths 1, 1.5, 2 respectively.
We see in fact that the width of the shell
increases going from the high to the low
from top to bottom)
and each column is for different times corresponding to cocoon lengths 1, 1.5, 2 respectively.
We see in fact that the width of the shell
increases going from the high to the low ![]() case. Moreover we can
see that the shell tends to widen and the bow shock becomes weaker
during the evolution of the cocoon, apart from the
case. Moreover we can
see that the shell tends to widen and the bow shock becomes weaker
during the evolution of the cocoon, apart from the ![]() case
in which the relative thickness of the shell remains constant.
Note that the localized feature appearing along the z=0 axis
is due to the assumed reflection boundary conditions and does not affect the
general morphological and dynamical behavior.
case
in which the relative thickness of the shell remains constant.
Note that the localized feature appearing along the z=0 axis
is due to the assumed reflection boundary conditions and does not affect the
general morphological and dynamical behavior.
In order to better quantify the deficit or the enhancement in the X-ray
emission, we have computed integral measures ![]() and
and ![]() of these
quantities defined as
of these
quantities defined as
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4150F5.ps}
\end{figure}](/articles/aa/full/2003/18/aah4150/Timg80.gif) |
Figure 5:
(Upper panels) Plot of the integrated flux deficit as a function
of cocoon length in the 0.1-4 keV band (left) and in the 4-10 keV band
( right) for the M=60 cases.
This quantity is
defined in Eq. (9).
(Lower panels) Plot of the excess emission as a function of cocoon length in the
0.1-4 keV band (left) and in the 4-10 keV band
(right) for the M=60 cases. This quantity is
defined in Eq. (10).
In the four panels the
three lines refer to the |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4150F6.ps}
\end{figure}](/articles/aa/full/2003/18/aah4150/Timg81.gif) |
Figure 6:
Temperature plots
for the M=120 cases (
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4150F7.ps}
\end{figure}](/articles/aa/full/2003/18/aah4150/Timg82.gif) |
Figure 7:
Temperature plots
for the M=60 cases (
|
| |
Figure 8:
Temperature plots
for the M=10, |
As we discussed, the shock driven in the external medium can heat it
and its effects can be more or less evident depending on its
strength. The heating of the shell can change the typical
emission energies, an example of the consequences of this effect has
been shown in the bottom panel of the first column of
Fig. 5 where we have seen that the case
with ![]() seemed to present an anomalous behavior. We can now
compare the first column of Fig. 5 with the second column where we
show the same quantities but in the range 4-10 keV. Looking at the
bottom panels we see that the case
seemed to present an anomalous behavior. We can now
compare the first column of Fig. 5 with the second column where we
show the same quantities but in the range 4-10 keV. Looking at the
bottom panels we see that the case ![]() ,
which in the softer
band presented an excess emission below that of the case
,
which in the softer
band presented an excess emission below that of the case
![]() ,
shows in the harder band an excess emission larger than the other cases.
The gas in the compressed shell becomes in fact hotter as we increase
the value of
,
shows in the harder band an excess emission larger than the other cases.
The gas in the compressed shell becomes in fact hotter as we increase
the value of ![]() and the emission is then shifted towards higher
emission energies. To quantify in more detail this temperature change, we
have plotted in the first row of Figs. 6-8
the quantity
and the emission is then shifted towards higher
emission energies. To quantify in more detail this temperature change, we
have plotted in the first row of Figs. 6-8
the quantity
From the figures we see that, for the cases with ![]() and M=60,120, the
shell temperature is everywhere larger than 8 keV and reaches
temperatures up to 850 keV at the jet head of the M=120 case. The lower density cases,
instead, present an increase in temperature mainly concentrated in the
forward part of the cocoon. This temperature distribution will have
consequences in the shell morphology as seen in different X-ray
bands. In fact, we expect to see emission from the forward part of the
cocoon at high energies, while the backward part is expected to be
more dominant at lower energies.
and M=60,120, the
shell temperature is everywhere larger than 8 keV and reaches
temperatures up to 850 keV at the jet head of the M=120 case. The lower density cases,
instead, present an increase in temperature mainly concentrated in the
forward part of the cocoon. This temperature distribution will have
consequences in the shell morphology as seen in different X-ray
bands. In fact, we expect to see emission from the forward part of the
cocoon at high energies, while the backward part is expected to be
more dominant at lower energies.
The first attempt to build an analytical model for the cocoon dynamics
is due to Begelman & Cioffi (1989) and Cioffi & Blondin (1992). They
consider only the case of strongly overpressured cocoons, for which
they consider only strong shocks driven in the external medium and
they essentially neglect the external pressure. For our purposes, we
have to extend the description to a more general situation, in which
the external shock can be of any strength and the external pressure is
taken into account. We describe in detail the model in the Appendix,
here we give only the resulting behavior of the extended cocoon
radius and cocoon pressure versus time: the cocoon radius is
given by
In a similar way we can also find a solution assuming a spherical symmetry
for the cocoon, that is solving the system of Eqs. (A.6-A.8) taking
![]() .
Taking into account separately the
strongly overpressured (
.
Taking into account separately the
strongly overpressured (
![]() )
and the weakly overpressured
(
)
and the weakly overpressured
(
![]() )
phases we can find two distinct regimes of expansion:
a supersonic one during which the external radius behaves like
)
phases we can find two distinct regimes of expansion:
a supersonic one during which the external radius behaves like
Looking at the geometry and at the detailed structure of the shell and the cocoon, these analytical models are too simplified to describe in detail the radiative properties of the cocoon but still they show clearly how the relative thickness of the shell can increase only in a weakly overpressured regime.
The cocoon expansion in a stratified medium is, of course, much more
complicated, since the external pressure is not constant, and the
development of an analytical model becomes more problematic. However
the above discussion can provide a framework for understanding the
results of numerical simulation.
Looking in more detail at the behavior of the extended cocoon radius,
we observe that, as expected from the discussion of the uniform case,
its expansion velocity decreases faster initially, when the cocoon is
strongly overpressured, and then decreases more slowly, when the shock
becomes weaker. Fitting a power law ![]()
![]() for the
quantities
for the
quantities ![]() ,
,
![]() ,
,
![]() in the initial and
terminal part of the evolution for the cases with M = 60, we get the
exponents
in the initial and
terminal part of the evolution for the cases with M = 60, we get the
exponents ![]() reported in Table 2. We see
that, at later times, the exponents of
reported in Table 2. We see
that, at later times, the exponents of ![]() become systematically larger than those
obtained at the initial times. Moreover we see that the differences
between the two exponents are larger for the lower density cases and
for
become systematically larger than those
obtained at the initial times. Moreover we see that the differences
between the two exponents are larger for the lower density cases and
for ![]() are minimal. In this last case, in fact the cocoon
stays strongly overpressured during the whole evolution.
are minimal. In this last case, in fact the cocoon
stays strongly overpressured during the whole evolution.
|
|
||
|
|
0.85 | 0.85 |
| 0.54 | 0.67 | |
| 0.43 | 0.56 | |
|
|
||
|
|
0.75 | 0.95 |
| 0.56 | 0.71 | |
| 0.45 | 0.53 | |
|
|
||
|
|
0.77 | 0.89 |
| 0.69 | 0.81 | |
| 0.46 | 0.07 |
A similar analysis can be done for the cocoon radius ![]() .
We see that
in the high and intermediate density cases the exponent for
.
We see that
in the high and intermediate density cases the exponent for ![]() also
increases but less than the exponent for
also
increases but less than the exponent for ![]() .
In the low density
case, instead,
.
In the low density
case, instead, ![]() becomes almost constant in time. This behavior
tells us that, when the cocoon is not any more strongly overpressured,
the relative shell thickness start to increase as it happened in the
homogeneous case. The behavior of the relative thickness of the shell
can be in fact derived from Table 2, since it is
related to the ratio
becomes almost constant in time. This behavior
tells us that, when the cocoon is not any more strongly overpressured,
the relative shell thickness start to increase as it happened in the
homogeneous case. The behavior of the relative thickness of the shell
can be in fact derived from Table 2, since it is
related to the ratio
![]() .
We then see that it has in general a
slower increase at the beginning of the evolution, and accelerates in
the following phases. As discussed above, the effects of not being
strongly overpressured are more evident by decreasing the value of
.
We then see that it has in general a
slower increase at the beginning of the evolution, and accelerates in
the following phases. As discussed above, the effects of not being
strongly overpressured are more evident by decreasing the value of ![]() and, in fact, the increase of the relative cocoon width is larger
for smaller
and, in fact, the increase of the relative cocoon width is larger
for smaller ![]() .
If we compare the cocoon widths for equal distances
of jet propagation we have a further effect that amplify the
consequences of the behavior discussed above, namely we have to take
into account that the advance velocity of the head of the jet
decreases when we decrease the value of
.
If we compare the cocoon widths for equal distances
of jet propagation we have a further effect that amplify the
consequences of the behavior discussed above, namely we have to take
into account that the advance velocity of the head of the jet
decreases when we decrease the value of ![]() .
.
In this section we have seen that the transition from a strongly overpressured cocoon to a cocoon which is essentially in pressure equilibrium with the surroundings leads to different properties of the shell of the compressed external material. In Sect. 5.3 we will try to see whether it is possible to determine in a more quantitative way how this transition depends on the jet physical parameters.
From the above discussion we have seen that the average cocoon pressure can be used for interpreting the cocoon dynamics and therefore determining the transition between the strong and weak shock regimes. In the case of uniform external medium, the cocoon pressure, after a decrease proportional to t-1, tends to a constant. In the present case, with a decreasing external pressure, we expect that the cocoon pressure does not tend to a constant but that it will tend to follow the behavior of P*, defined in Eq. (A.7).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4150F10.ps}
\end{figure}](/articles/aa/full/2003/18/aah4150/Timg115.gif) |
Figure 10:
Plot of the pressure vs. cocoon length. The rows refer to the
different Mach numbers while columns to the different |
In Fig. 10 we have plotted the behavior of ![]() (solid curve) and P* (dashed curve) against the cocoon length, where
(solid curve) and P* (dashed curve) against the cocoon length, where ![]() is the
average cocoon pressure and P* is the external pressure averaged
over the cocoon volume. The ratio between the two quantities gives a
measure of the average strength of the shock driven in the external
medium.
Looking at the behavior of the cocoon evolution in the different cases we
have an always strongly overpressured expansion for the cases M=120 and
is the
average cocoon pressure and P* is the external pressure averaged
over the cocoon volume. The ratio between the two quantities gives a
measure of the average strength of the shock driven in the external
medium.
Looking at the behavior of the cocoon evolution in the different cases we
have an always strongly overpressured expansion for the cases M=120 and
![]() and for M=60 and
and for M=60 and ![]() ,
in these three cases the transition length
would be larger than the actual longitudinal size of our domain; two cases showing
a transition from strongly overpressured to weakly overpressured cocoons for M=120,
,
in these three cases the transition length
would be larger than the actual longitudinal size of our domain; two cases showing
a transition from strongly overpressured to weakly overpressured cocoons for M=120, ![]() and
M=60,
and
M=60, ![]() ;
finally we have two cases where the cocoon is
always weakly overpressured,
i.e. for M=60,
;
finally we have two cases where the cocoon is
always weakly overpressured,
i.e. for M=60, ![]() and M=10,
and M=10, ![]() .
This is in agreement with
the discussion on the X-ray flux distributions following Figs. 1-3.
.
This is in agreement with
the discussion on the X-ray flux distributions following Figs. 1-3.
In order to determine the length of the cocoon at which the transition occurs, we look for
a scaling law for the quantity
![]() as a function of the parameters
as a function of the parameters ![]() ,
M and
,
M and ![]() during the initial strongly overpressured phase.
Taking into account only the cases that are stronlgy overpressured at the beginning of the evolution,
we notice that the initial decrease of the average cocoon pressure follows a similar
behavior for all the cases that we have considered:
with a power law fit
during the initial strongly overpressured phase.
Taking into account only the cases that are stronlgy overpressured at the beginning of the evolution,
we notice that the initial decrease of the average cocoon pressure follows a similar
behavior for all the cases that we have considered:
with a power law fit
![]() to the
initial evolution of the different cases we find a mean value
to the
initial evolution of the different cases we find a mean value
![]() with
an uncertainness of 10%.
In Table 3 we show the
values of the quantity
with
an uncertainness of 10%.
In Table 3 we show the
values of the quantity
![]() at the beginning of the evolution,
when the cocoon length is one third the core radius and the cocoon is
typically strongly overpressured (notice that the cases
M=10,
at the beginning of the evolution,
when the cocoon length is one third the core radius and the cocoon is
typically strongly overpressured (notice that the cases
M=10, ![]() and M=60,
and M=60, ![]() make an exception). These values can be
represented, with good approximation by the scaling
make an exception). These values can be
represented, with good approximation by the scaling
![]() .
The general scaling law thus becomes:
.
The general scaling law thus becomes:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4150F11.ps}
\end{figure}](/articles/aa/full/2003/18/aah4150/Timg123.gif) |
Figure 11:
Plot of the values of
|
Of course the transition from a strongly
to a weakly overpressured regime is not sudden, but gradually happens when
![]() becomes of the order of unity. Setting a constant value for
becomes of the order of unity. Setting a constant value for
![]() of this order
in Eq. (19)
we derive the scaling law for transition length
of this order
in Eq. (19)
we derive the scaling law for transition length
![]() (as we have done
for the uniform case, see Eq. (14)).
(as we have done
for the uniform case, see Eq. (14)).
In Sects. 3-5 we have seen that strongly
and weakly overpressured cocoons present different X-ray
morphologies. The former ones will show no deficit of emission
accompanied by a strong
emission from a shell marking the shock, driven by the cocoon
expansion. The material in the shell will be much hotter than the
ambient medium, the shell emission will then be shifted to higher
frequencies and therefore more visible at higher
X-ray energies, especially near the jet head. Weakly
overpressured cocoons will be instead characterized by the presence of a
deficit of emission in the cocoon, while the emission from the shell will be much
less visible than in the previous case; in addition, the material in the shell will be
essentially at the same temperature as the ambient medium and there
will be no change in the emission spectrum. These two regimes depend
on the jet physical parameters and on the age of the cocoon.
High Mach
number jets with high densities will be strongly overpressured for a
longer fraction of their life, decreasing the density and the Mach
number the transition to weakly overpressured cocoon will occur at an
earlier stage. We have found that the scaling of the transition
length from one regime to the other is given to a good approximation by
Eq. (20). Fixing a length of the cocoon, from this
equation we can then obtain a relation between Mach number and density
ratio such as
![]() .
This scaling law has been
represented in Fig. 12 with the dotted, dashed and
dash-dotted lines for cocoon lengths equal to 0.5, 1 and 2 core
radii respectively. The proportionality constant
.
This scaling law has been
represented in Fig. 12 with the dotted, dashed and
dash-dotted lines for cocoon lengths equal to 0.5, 1 and 2 core
radii respectively. The proportionality constant
![]() has been set
to fulfill the transition conditions in the cases where the
transition between the two regimes is observed, i.e.
has been set
to fulfill the transition conditions in the cases where the
transition between the two regimes is observed, i.e.
![]() and
and
![]() .
In the same figure we can
also notice the presence of another line, that individuates a region in
which the jet becomes subsonic with respect to its internal sound
speed.
.
In the same figure we can
also notice the presence of another line, that individuates a region in
which the jet becomes subsonic with respect to its internal sound
speed.
|
M \ |
0.1 | 0.01 | 0.001 |
| 120 | 192.03 | 31.30 | 6.99 |
| 60 | 34.35 | 8.13 | 2.17 |
| 10 | 0.99 |
Since Mach number and density ratio are physically very meaningful
parameters, but cannot be determined for actual jets, it is favorable
to express the scaling relation in terms of the jet kinetic power.
In order to do so, we make use of Eq. (21)
where ![]() is a quantity that depends on the properties of the
environment. From this relation we see that jets with the same
kinetic power have the same transition length
between the two phases. The curves in Fig. 12
separating the strongly and weakly overpressured regimes, which are
given by
is a quantity that depends on the properties of the
environment. From this relation we see that jets with the same
kinetic power have the same transition length
between the two phases. The curves in Fig. 12
separating the strongly and weakly overpressured regimes, which are
given by
![]() ,
will therefore correspond
also to a constant value of
,
will therefore correspond
also to a constant value of
![]() .
These
considerations tell us that the separation between the two regimes is
essentially determined by the jet kinetic power: the transition will
occur at higher values of
.
These
considerations tell us that the separation between the two regimes is
essentially determined by the jet kinetic power: the transition will
occur at higher values of ![]() for high kinetic power jets and at lower
for high kinetic power jets and at lower ![]() for low kinetic power jets.
For instance the dashed curve shown in Fig. 12 representing the separation between the two regimes for
a cocoon length equal to 2 core radii
corresponds to
for low kinetic power jets.
For instance the dashed curve shown in Fig. 12 representing the separation between the two regimes for
a cocoon length equal to 2 core radii
corresponds to
![]() .
The properties of the environment enter in the parameter
.
The properties of the environment enter in the parameter ![]() that fixes
a measure for the jet kinetic power.
For a typical cluster environment with
a central density
that fixes
a measure for the jet kinetic power.
For a typical cluster environment with
a central density
![]() ,
a core radius 100 kpc
and a temperature 3 keV we have
,
a core radius 100 kpc
and a temperature 3 keV we have
![]() and the dividing kinetic power for a cocoon length equal to 1.5 core radii
will be
and the dividing kinetic power for a cocoon length equal to 1.5 core radii
will be
![]() .
It is important to notice that for jets that are slightly
supersonic with respect to their internal sound speed the jet enthalpy flux
becomes comparable to the kinetic one. In these cases our estimates for
the jet kinetic power should be corrected at most by a factor two in order to
obtain an approximation of the total power of the jet.
.
It is important to notice that for jets that are slightly
supersonic with respect to their internal sound speed the jet enthalpy flux
becomes comparable to the kinetic one. In these cases our estimates for
the jet kinetic power should be corrected at most by a factor two in order to
obtain an approximation of the total power of the jet.
Considering the particular case of Cygnus A, its cluster
environment is characterized by a central density
![]() ,
a core radius 35 kpc and a temperature 3.4 keV
(Carilli et al. 1994), giving
,
a core radius 35 kpc and a temperature 3.4 keV
(Carilli et al. 1994), giving
![]() .
The radio lobes of Cygnus A
show an extent of
.
The radio lobes of Cygnus A
show an extent of ![]() 70 kpc, twice the core radius
(
70 kpc, twice the core radius
(
![]() ). For this
length the dividing power is given by
). For this
length the dividing power is given by
![]() ,
as it is possible to see in Fig. 12. Since Cygnus A clearly
shows deficit of X-ray emission and therefore is in a weakly overpressured
regime, these estimates give an upper limit to the kinetic power of its jet
,
as it is possible to see in Fig. 12. Since Cygnus A clearly
shows deficit of X-ray emission and therefore is in a weakly overpressured
regime, these estimates give an upper limit to the kinetic power of its jet
![]()
![]() .
Nevertheless the pressure of the
expanding cocoon must be higher than the ambient one since observations
by Chandra (Smith et al. 2002) show clearly that the shell is slightly
hotter than the surrounding medium. Then the cocoon is still expanding
as a (weak) shock wave more than a sound wave.
.
Nevertheless the pressure of the
expanding cocoon must be higher than the ambient one since observations
by Chandra (Smith et al. 2002) show clearly that the shell is slightly
hotter than the surrounding medium. Then the cocoon is still expanding
as a (weak) shock wave more than a sound wave.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4150F12.ps}
\end{figure}](/articles/aa/full/2003/18/aah4150/Timg141.gif) |
Figure 12:
Representation of the different regimes of the cocoon expansion in the
|
Another well known example of the interaction between a radio source and
the thermal gas of a cluster is the FR I type radio galaxy 3C 84 inside the
Perseus cluster. The cluster core can be modeled with a central electron
density
![]() ,
a core radius
,
a core radius ![]() kpc and a central
temperature
kpc and a central
temperature
![]() keV (Schmidt et al. 2002) yielding
keV (Schmidt et al. 2002) yielding
![]() .
The radio lobes show an average extent of
.
The radio lobes show an average extent of ![]() 22 kpc, giving a dividing power
22 kpc, giving a dividing power
![]() .
These
estimates give an upper limit on the kinetic luminosity of the jet
.
These
estimates give an upper limit on the kinetic luminosity of the jet
![]() .
This upper limit can be lowered
considering that the shell of enhanced emission surrounding the cavities
contains clearly the X-ray coolest gas in the cluster (Fabian et al. 2001).
This fact rules out
the presence of strong shocks driven by the expanding cocoon. In our scheme
this means that the cocoon must be in a weakly overpressured regime in the
first phase of expansion yet as for example in the case M=10,
.
This upper limit can be lowered
considering that the shell of enhanced emission surrounding the cavities
contains clearly the X-ray coolest gas in the cluster (Fabian et al. 2001).
This fact rules out
the presence of strong shocks driven by the expanding cocoon. In our scheme
this means that the cocoon must be in a weakly overpressured regime in the
first phase of expansion yet as for example in the case M=10, ![]() .
As it can be seen in Fig. 8 the average temperature of the shell for this
simulation is equal to the ambient one and in the shell there is also emission from gas cooler
than the ambient one. This cooling is due to the adiabatic expansion
of the shell after being compressed by a weak shock, in a way similar to that
described in the simulations of expanding hot bubbles
by Brighenti & Mathews (2002). Taking this
case (
.
As it can be seen in Fig. 8 the average temperature of the shell for this
simulation is equal to the ambient one and in the shell there is also emission from gas cooler
than the ambient one. This cooling is due to the adiabatic expansion
of the shell after being compressed by a weak shock, in a way similar to that
described in the simulations of expanding hot bubbles
by Brighenti & Mathews (2002). Taking this
case (
![]() )
to determine a limit on the kinetic power of the jet
we obtain
)
to determine a limit on the kinetic power of the jet
we obtain
![]() .
For deriving the total jet power this estimate should be corrected by the enthalpy
term, that for the above values of M and
.
For deriving the total jet power this estimate should be corrected by the enthalpy
term, that for the above values of M and ![]() is approximately equal to the 30% of the kinetic power.
This estimate is similar to the
one by Fabian et al. (2001) who used the analytical bubble model by Churazov et al. (2000) to
determine their limits. This substantial agreement can be understood considering that
the Churazov et al. (2000) model solves exactly Eq. (A.4) with spherical symmetry
assuming that the bubble pressure is equal to the external one.
The limits of Fabian et al. (2001) are then determined requiring
that the bubble has the observed dimensions, that it expands subsonically
and that it is not buoyant. This situation is similar to what we refer to as a weakly
or not overpressured regime.
The great difference between our low power cases
and a hot underdense bubble is the presence of the highly collimated jet that forms
a thermal hot spot and is likely not effective in uplifting
the cooling flow gas as proposed for example by
Soker et al. (2002) to explain the presence of cool gas in the rims around the cavities.
A collimated jet tends to go through the gas of the cluster displacing it aside and
without uplifting it. Once the jet has terminated its active phase is rapidly
destroyed (Reynolds et al. 2002) and the lobes can evolve like
buoyant bubbles (see for example Churazov et al. 2001 or Quilis et al. 2001).
An example similar to Perseus A is the Hydra A cluster containing the powerful FR I radio
source 3C 218. Given the properties of the X-Ray gas (
is approximately equal to the 30% of the kinetic power.
This estimate is similar to the
one by Fabian et al. (2001) who used the analytical bubble model by Churazov et al. (2000) to
determine their limits. This substantial agreement can be understood considering that
the Churazov et al. (2000) model solves exactly Eq. (A.4) with spherical symmetry
assuming that the bubble pressure is equal to the external one.
The limits of Fabian et al. (2001) are then determined requiring
that the bubble has the observed dimensions, that it expands subsonically
and that it is not buoyant. This situation is similar to what we refer to as a weakly
or not overpressured regime.
The great difference between our low power cases
and a hot underdense bubble is the presence of the highly collimated jet that forms
a thermal hot spot and is likely not effective in uplifting
the cooling flow gas as proposed for example by
Soker et al. (2002) to explain the presence of cool gas in the rims around the cavities.
A collimated jet tends to go through the gas of the cluster displacing it aside and
without uplifting it. Once the jet has terminated its active phase is rapidly
destroyed (Reynolds et al. 2002) and the lobes can evolve like
buoyant bubbles (see for example Churazov et al. 2001 or Quilis et al. 2001).
An example similar to Perseus A is the Hydra A cluster containing the powerful FR I radio
source 3C 218. Given the properties of the X-Ray gas (![]() kpc,
kpc,
![]() ,
,
![]() keV, David et al. 2001) and a cocoon length of
keV, David et al. 2001) and a cocoon length of ![]() 49 kpc
we obtain an upper limit on the jet power
49 kpc
we obtain an upper limit on the jet power
![]() .
Since
there is no indication that the gas surrounding the radio lobes is hotter than the ambient
cluster gas this limit can be lowered at least by an order of magnitude.
On the other hand it is possible to find some examples of radio sources inside galaxy clusters
that do not show the presence of X-ray cavities. In our scheme these sources could correspond
to radio lobes still in a strongly overpressured phase. For example the FR II radio source 3C 295
is found inside a cluster whose core is characterized by a radius
.
Since
there is no indication that the gas surrounding the radio lobes is hotter than the ambient
cluster gas this limit can be lowered at least by an order of magnitude.
On the other hand it is possible to find some examples of radio sources inside galaxy clusters
that do not show the presence of X-ray cavities. In our scheme these sources could correspond
to radio lobes still in a strongly overpressured phase. For example the FR II radio source 3C 295
is found inside a cluster whose core is characterized by a radius
![]() kpc, a central
density
kpc, a central
density
![]() and a temperature
and a temperature
![]() keV
(Allen et al. 2001). This cluster does not show any cavity in its X-ray emission.
Given the longitudinal dimension of the radio source
keV
(Allen et al. 2001). This cluster does not show any cavity in its X-ray emission.
Given the longitudinal dimension of the radio source ![]() 17.6 kpc we can estimate
a lower limit of the jet power
17.6 kpc we can estimate
a lower limit of the jet power
![]() .
.
In this paper we performed numerical simulations of axisymmetric supersonic jets propagating in an isothermal background atmosphere. In agreement with the results presented by Reynolds et al. (2001), we find two distinct and subsequent regimes of interaction between the cocoon and the external medium. In the first phase of evolution, the overpressured cocoon drives a strong shock in the ambient medium, forming a thin, hot and compressed shell of shocked material, in the second phase the shock becomes very weak and the shell widens, decreasing its density and temperature. The resulting X-ray morphology in the two phases is different: in the strongly overpressured phase, we expect a shell of enhanced X-ray emission surrounding the radio emitting material, while, in the weak shock phase, we expect a deficit of X-ray emission coincident with the radio lobes. We have studied the dependence of the transition between these two phases on the physical jet parameters, by a wide coverage of the parameter space and by a comparison of the results of numerical simulations with analytical models. We find that the transition length between the two regimes depends essentially only on the jet power scaled over a value dependent on the properties of the ambient medium.
Acknowledgements
The authors acknowledge the italian MIUR for financial support, grant No. 2001-028773. The numerical calculations have been performed at CINECA in Bologna, Italy, thanks to the support of INAF.
As we have discussed, the jet replenishes the cocoon
of matter and energy, therefore the cocoon expands compressing the
ambient medium and if the expansion speed of the cocoon is highly
supersonic, it will drive a strong shock in the external medium.
The first attempts to give an analytic description of theses processes
was done by Begelman & Cioffi (1989) and Cioffi &
Blondin (1992). To describe the energy input by the jet, they write
the following energy equation for the extended cocoon