A&A 402, 1115-1127 (2003)
DOI: 10.1051/0004-6361:20030175
Information entropy in solar atmospheric fields
I. Intensity photospheric structures
G. Consolini1 - F. Berrilli2,1 - A. Florio1,2 - E. Pietropaolo3, 1 -
L. A. Smaldone4
1 - Istituto di Fisica dello Spazio Interplanetario-CNR, 00133 Roma, Italy
2 -
Dipartimento di Fisica, Università di Roma Tor Vergata, 00133 Roma, Italy
3 -
Dipartimento di Fisica, Università di L'Aquila, 67010 L'Aquila, Italy
4 -
Dipartimento di Scienze Fisiche, Università di Napoli Federico II, 80126 Napoli, Italy
Received 30 July 2002 / Accepted 31 January 2003
Abstract
The existence of a quasi-regular pattern in solar photospheric convective fields is an
open question. In
the present work, this problem is quantitatively approached by means of the normalised information
entropy measure H'(r) as introduced by Van Siclen (1997), which reports on the information
content at different scales. Images were acquired at the THEMIS telescope of the European Northern
Observatory by the IPM observing mode, and at the Richard B. Dunn Solar Telescope of the National
Solar Observatory.
The evaluation of H'(r) in the case of photospheric intensity binarized images
shows the presence of maxima which are evidence of different prominent scales in the photospheric pattern.
The relative positions of these maxima defines an ordering scale 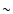 1.6 Mm in both instantaneous
and average images. This is read as the evidence of a spatio-temporal organization in the evolution of
convective pattern. The emergence of an ordering scale is discussed in the framework of pattern formation
in random systems and in connection with the findings of previous works.
1.6 Mm in both instantaneous
and average images. This is read as the evidence of a spatio-temporal organization in the evolution of
convective pattern. The emergence of an ordering scale is discussed in the framework of pattern formation
in random systems and in connection with the findings of previous works.
By averaging images with time,
an increase of the information content characterized by a coherence time of 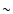 1 h is observed in the
range of scales from 5.0 Mm to 10.0 Mm.
1 h is observed in the
range of scales from 5.0 Mm to 10.0 Mm.
Key words: Sun: photosphere -
Sun: granulation -
methods: statistical
The solar external layers show the effects of several
physical processes occurring at different scales and depths in the Sun. Among these processes a
special role is played by the convection, the main kind of energy transport in the subsurface
layers. In the past, different observational and analytical methods pointed out the existence of
different relevant length scales related to different patterns.
The granulation is the best documented and evident photospheric intensity pattern. It is directly visible
in high resolution broadband intensity or Doppler velocity images (Spruit et al.
1990). This granulation pattern consists of an assembly of convection cells, composed by a central plasma upflow surrounded by a structured network of downflows, where hydrodynamic instabilities,
as recently suggested by numerical simulations, play an important role in the generation of the
granulation pattern (Stein & Nordlund 1998; Rast 1999). These granular cells are
characterized by a typical horizontal extent of
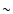 1.4 Mm (Lawrence et al. 1999), and their typical lifetime ranges
from few minutes to
1.4 Mm (Lawrence et al. 1999), and their typical lifetime ranges
from few minutes to 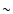 15 min.
However, in spite of these short
lifetimes, a prolonged persistence
of the granulation pattern and/or of related photospheric structures has been reported in several
studies (Baudin et al. 1997; Roudier et al. 1997; Hoekzema et al.
1998; Müller et al. 2001; Getling & Brandt 2002).
In particular, averaging many hours (
15 min.
However, in spite of these short
lifetimes, a prolonged persistence
of the granulation pattern and/or of related photospheric structures has been reported in several
studies (Baudin et al. 1997; Roudier et al. 1997; Hoekzema et al.
1998; Müller et al. 2001; Getling & Brandt 2002).
In particular, averaging many hours (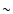
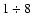 )
of observations, Getling & Brandt (2002)
revealed quasi-regular structures of the photospheric and subphotospheric flows, that suggests the
existence of a previously unknown type of self-organization resembling the so-called target patterns
observed in experiments on Rayleigh-Bénard convection. However, this point of view has been recently
discussed by Rast (2002), who suggested the granulation field to be consistent with a completely
random and changing flow pattern, not-requiring self-organization.
)
of observations, Getling & Brandt (2002)
revealed quasi-regular structures of the photospheric and subphotospheric flows, that suggests the
existence of a previously unknown type of self-organization resembling the so-called target patterns
observed in experiments on Rayleigh-Bénard convection. However, this point of view has been recently
discussed by Rast (2002), who suggested the granulation field to be consistent with a completely
random and changing flow pattern, not-requiring self-organization.
A less evident pattern is associated with mesogranulation, firstly reported
by November et al. (1981) on the basis of the analysis of Doppler velocity fields. The mesogranular
field seems to be characterized by an intermediate range of scales (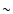
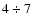 Mm) lying between
granulation and supergranulation ones. As pointed out by Rieutord et al. (2000), although
different approaches have been applied to the study of mesogranulation pattern, the emerging picture is
foggy and controversial. The physical origin of mesogranulation is still an
open question.
Besides the
traditional account of mesogranulation as cellular convection driven by superadiabaticity in the deeper
layer, where neutral helium ionizes, some authors state a subsurface convective nature of mesogranular
pattern (Ploner et al. 2000). Conversely, Rieutord et al. (2000) argued that
mesogranulation is due to a combination of strong positive divergences, induced by highly energetic
granules, and averaging effects of image analysis. Simulations by Cattaneo et al.
(2001) support the idea that mesogranules owe their origin to collective interactions between
the granules. Moreover, Lawrence et al. (1999) underlined the relevance of a turbulent component in
the horizontal flows at the same mesogranular scales.
Mm) lying between
granulation and supergranulation ones. As pointed out by Rieutord et al. (2000), although
different approaches have been applied to the study of mesogranulation pattern, the emerging picture is
foggy and controversial. The physical origin of mesogranulation is still an
open question.
Besides the
traditional account of mesogranulation as cellular convection driven by superadiabaticity in the deeper
layer, where neutral helium ionizes, some authors state a subsurface convective nature of mesogranular
pattern (Ploner et al. 2000). Conversely, Rieutord et al. (2000) argued that
mesogranulation is due to a combination of strong positive divergences, induced by highly energetic
granules, and averaging effects of image analysis. Simulations by Cattaneo et al.
(2001) support the idea that mesogranules owe their origin to collective interactions between
the granules. Moreover, Lawrence et al. (1999) underlined the relevance of a turbulent component in
the horizontal flows at the same mesogranular scales.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H3893F1.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg14.gif) |
Figure 1:
An image made by a regular distribution of randomly oriented U, and including two
structures, the former consisting of U letters uniformly oriented,
the latter of randomly oriented T. of the two structures only one is easily visible
(adapted from Legrenzi 2002). |
The recognition of quasi-regular topologies in natural patterns may be approached qualitatively by
eyes and/or quantitatively by numerical methods. However, the study of natural patterns
requires the definition of non-subjective quantities that may
help to characterize the emergent
regularities. In order to clarify the above concepts let us refer to the pattern reported in
Fig. 1. Although at a first look only one ordered structure is evident, the pattern also
contains a second ordered structure. As a matter of fact, this pattern consists of randomly
oriented U letters plus two square structures made of T letters randomly oriented (top right region) and of
U letters with the same orientation (bottom left region). This example clearly demonstrates that the
classification of patterns by eye may be misleading. Thus, non-subjective methods are required for the
study of natural patterns.
In the present work, we quantitatively investigate the existence, the relevance and the nature of some
scales in the photospheric fields by means of the normalised information entropy as
introduced by Van Siclen (1997), focusing our attention on granulation pattern. Using this new
analytical approach, which is based on Shannon's information theory, we check the possible
existence of a nearly ordered topology of the granular structures in single and time-averaged photospheric
intensity fields. Here, the term "topology'' refers to how the granulation structures are arranged in the photospheric field.
The paper is structured as follows. In Sect. 2 we present a brief mathematical description of the
information entropy approach along with the results of some numerical simulations on ordered and
disordered topologies. Section 3 is completely devoted to the description of the
photospheric observations and of the image reduction and processing. Section 4 will present the results of
the investigation on the topology of the granular structures in both single and time-averaged photospheric
intensity images. A discussion of the results is also given in this section. We conclude the work with
Sect. 5 where the summary and the conclusions of our analysis are reported. Appendix A reports the
results of the information entropy method on some meaningful simulated patterns.
The investigation and the characterization of the solar granulation pattern may benefit by
statistical-mathematical methods introduced in different physical frameworks. In detail, in the field
of matter physics it was clearly shown that the study of the topology and the evolution of correlated
random structures may take advantage of the application of Shannon's information theory (Shannon & Weaver
1959; Beck & Schlögl 1993).
As a matter of fact, morphology and topology information may be extracted by applying the Gibbs-Shannon
entropy concept. For example, Andraud et al. (1994, 1997) introduced an entropic
measure, named configuration entropy, as a descriptor of random morphologies. Such configuration
entropy is a measure of the local fluctuations of some measurable quantity over the random system, defined
as follows.
Let us consider a
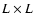 binarized (black and white) image of some physical
observable quantity, and a square sliding cell of side length
l containing a=l2 pixels. If Nk (a) is the number of cells of size a containing kblack pixels, and N is the total number of sliding cells, then we can define a set of relative
frequencies pk (a), as estimators for probabilities, according to the following expression:
binarized (black and white) image of some physical
observable quantity, and a square sliding cell of side length
l containing a=l2 pixels. If Nk (a) is the number of cells of size a containing kblack pixels, and N is the total number of sliding cells, then we can define a set of relative
frequencies pk (a), as estimators for probabilities, according to the following expression:
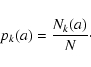 |
(1) |
Henceforth, the configuration entropy H*(a) will follow according to the definition:
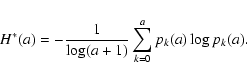 |
(2) |
Such a definition is equivalent to the usual Gibbs-Shannon entropy normalised by the factor
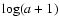 ,
which plays a role similar to the "multiplicative renormalization in the theory of
critical phenomena" (Andraud et al. 1997). When applied to a disordered system, this
entropic measure is able to extract some useful information dealing with the typical length scale at which
inhomogeneities are present and so on.
,
which plays a role similar to the "multiplicative renormalization in the theory of
critical phenomena" (Andraud et al. 1997). When applied to a disordered system, this
entropic measure is able to extract some useful information dealing with the typical length scale at which
inhomogeneities are present and so on.
A more sensitive measure of the morphological complexity in random system was introduced by Van
Siclen (1997). This measure was called information entropy H(l) because of its
ability to extract the average information content at a certain length scale l. Moreover, this
measure is able to keep information on clustering effects, as well as on periodicity or
ordering. According to the information theory, the information content of a system in a
configuration i is directly proportional to
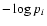 ,
where pi is the a priori probability of finding the system in the ith
configuration. When the information content is averaged over all the possible choices it defines
the information entropy H. Moreover, to make such a measure more sensitive to the structures at
the different scale Van Siclen introduced the normalised information entropy measure
,
where pi is the a priori probability of finding the system in the ith
configuration. When the information content is averaged over all the possible choices it defines
the information entropy H. Moreover, to make such a measure more sensitive to the structures at
the different scale Van Siclen introduced the normalised information entropy measure
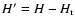 ,
where
,
where 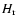 is the expected information entropy for a completely random system and H is the actual
information entropy. Let us briefly resume how to evaluate such a quantity.
is the expected information entropy for a completely random system and H is the actual
information entropy. Let us briefly resume how to evaluate such a quantity.
Consider a two-level image consisting of a collection of N black pixels placed on a square grid
of side length L, and a
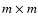 box. Let it be pi the probability of finding exactly
i black pixels of the N in a
box. Let it be pi the probability of finding exactly
i black pixels of the N in a
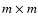 box if the black pixels were perfectly distributed in
the random fashion. Then,
box if the black pixels were perfectly distributed in
the random fashion. Then,
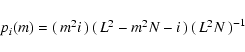 |
(3) |
where i ranges from
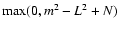 to
to
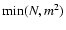 .
From here it follows that the
reference information entropy of a finite, perfectly random, system is
.
From here it follows that the
reference information entropy of a finite, perfectly random, system is
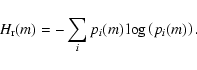 |
(4) |
On the other hand, the information entropy H(m) for the actual configuration is
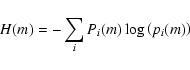 |
(5) |
where Pi(m) is the actual probability of finding i black pixels in any
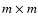 box, and pi(m) is defined according to Eq. (3). Therefore, the normalised
information entropy will be
box, and pi(m) is defined according to Eq. (3). Therefore, the normalised
information entropy will be
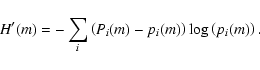 |
(6) |
On the basis of the definition of H'(m) we should expect that for a completely random distribution of a
collection of N black pixels H'(m) = 0 at each length scale m. In Fig. 2 we report the
behaviour of H' averaged on an ensemble of several
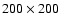 two-level images containing approx.
4000 black pixels pseudorandomly distributed. As expected H'(m) is very close to zero over the entire
analyzed range of scales. The slight deviations from zero should be read as the effect of a sporadic random
aggregation of some black pixels, as well as from finite size effects. We remark that the range of scales
investigated has been limited to half of the linear size of the images (
two-level images containing approx.
4000 black pixels pseudorandomly distributed. As expected H'(m) is very close to zero over the entire
analyzed range of scales. The slight deviations from zero should be read as the effect of a sporadic random
aggregation of some black pixels, as well as from finite size effects. We remark that the range of scales
investigated has been limited to half of the linear size of the images (
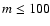 )
to avoid the
artifacts of this analysis at larger scales due to the decreasing significativity of the box statistics (Van Siclen 1997).
)
to avoid the
artifacts of this analysis at larger scales due to the decreasing significativity of the box statistics (Van Siclen 1997).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H3893F2.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg31.gif) |
Figure 2:
H'(m) versus m for a pseudorandom distribution of approx. 4000 black
pixels. H' has been averaged over an ensemble of 100 different configurations. |
Figure 3 shows a
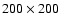 two-level image obtained from a pseudorandom
uniform distribution of the same square structure of linear dimension
two-level image obtained from a pseudorandom
uniform distribution of the same square structure of linear dimension
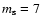 pixels around the sites of a periodic square lattice with a lattice constant
pixels around the sites of a periodic square lattice with a lattice constant
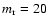 pixels.
pixels.
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{H3893F3.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg32.gif) |
Figure 3:
A pseudorandom uniform distribution of
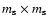 square structures
(with
square structures
(with
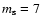 )
around the sites of a square lattice with a lattice constant )
around the sites of a square lattice with a lattice constant
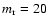 pixels. We remark that each structure is distributed inside the square cell centred on each lattice
site. pixels. We remark that each structure is distributed inside the square cell centred on each lattice
site. |
The results of the H' analysis on the pattern reported in Fig. 3 are shown in
Fig. 4. The behaviour of H' as a function of the sliding box dimension m reveals the
presence of several maxima that, according to Van Siclen (1997), can be read as follows. The
first maximum, which occurs at
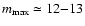 pixels, is related with the lattice constant
pixels, is related with the lattice constant
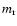 and the structure dimension
and the structure dimension 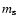 .
The additional maxima reveal the existence of clusters of structures.
.
The additional maxima reveal the existence of clusters of structures.
With reference to Fig. 4, in order to extract information on the preminent clustering scales, and
to provide some insights on the ordered topology, we decompose the H' into a superposition of several
contribution functions, as follows:
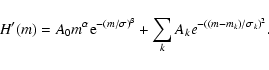 |
(7) |
The first contribution on the right hand refers to the asymmetric first peak, while the
second one is a superposition of Gaussian functions centred at mk. Although the decomposition is not
unique, the suggested one allows to reveal the existing hidden periodicity of the square
lattice. This is particularly evident when the peak positions of the different contributions are plotted
versus the odd numbers (see Fig. 5). As a matter of fact, the following relationship is found:
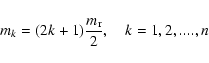 |
(8) |
where 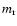 is lattice constant. This is to say that the investigation of maxima positions can
give some information on the existence of a nearly-ordered hidden lattice structure, although we cannot
say anything about the real geometry of the hidden ordering. In passing through, we underline that the
position of the first asymmetric peak (indicated with k=0 in Eq. (8)) has not been considered in
the fitting procedure, being affected by the dimension of the structures and of the empty zones as
discussed by Van Siclen (1997).
is lattice constant. This is to say that the investigation of maxima positions can
give some information on the existence of a nearly-ordered hidden lattice structure, although we cannot
say anything about the real geometry of the hidden ordering. In passing through, we underline that the
position of the first asymmetric peak (indicated with k=0 in Eq. (8)) has not been considered in
the fitting procedure, being affected by the dimension of the structures and of the empty zones as
discussed by Van Siclen (1997).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F4.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg38.gif) |
Figure 4:
The normalised information entropy H' (empty squares) relative to the pattern
reported in Fig. 3. Solid lines refer to the single contributions derived by
fitting H' using Eq. (7) with k=4. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F5.eps} \end{figure}](/articles/aa/full/2003/18/aah3893/Timg39.gif) |
Figure 5:
The peak positions mk derived from the decomposition of H' plotted versus
odd numbers. The solid line is a linear best fit using Eq. (7). The resulting lattice constant is
![$m_{\rm r} = [20.0 \pm 0.2]$](/articles/aa/full/2003/18/aah3893/img4.gif) . . |
Before going on, let us briefly discuss and comment what is different in this kind of analysis with
respect to the more usual techniques based on Fourier and/or wavelet transforms. The main difference among
these methods of analysis is that the normalised information entropy H' analysis, being based on a
probability measure, does not require any preliminary choice of an ad hoc set of functions or
waveforms (sine-cosine waves, plane waves, wavelets, etc.) in order to decompose the field/image under
investigation. Moreover, because the Fourier spectrum is related to the autocorrelation
function over the field, in order to observe strong signatures of periodicities using these
techniques, structures should be all of the same type
(i.e. have the same shape), all
oriented in the same direction, and all located in the
same position inside any elementary cell. When these
conditions are not fulfilled, spurious results may be found in terms of broad-band spectra (i.e. peaks may not be detectable). On the other hand, although wavelet analysis has a greater capability in finding localised
isolated structures and in extracting characteristic scales, when the results are discussed in terms of
spectra, this technique does not differ substantially from the Fourier transform (Lawrence et al. 2001;
Starck et al. 1998). Conversely, the normalised information entropy H' analysis,
looking for regularities by using a probabilistic approach, is less affected by the aforementioned aspects. In
other words, while Fourier analysis looks for periodicities in the field and wavelet analysis looks for
characteristic scales, the normalised information entropy H' analysis is able to extract information on
the presence of statistical regularities in the mutual positions of the structures.
In order to investigate photospheric features we used two datasets
of quiet granulation frames,
at disk center, obtained at the THEMIS telescope of the European
Northern Observatory (Tenerife)
and at the Richard B. Dunn Solar Telescope (DST) of the
National Solar Observatory (Sacramento
Peak).
The THEMIS telescope (Observatorio del Teide, Tenerife) time series consists of broadband (5 nm
FWHM around 557 nm) and monochromatic (2.1 pm FWHM) images and has been acquired on July 1,
1999 (from 7:21 to 8:24 UT) with the IPM observing mode. This mode
uses an Universal Birefringent
Filter followed by a Fabry-Pérot interferometer (Cavallini 1998).
The images were
acquired with a broadband camera and, simultaneously, with a
monochromatic camera at different
spectral points. A more thorough description can be found in Berrilli et al. (2002).
Each spectral series consisted of 19 broadband and 19
monochromatic images. The images were
acquired with two different integration times, 40 ms and 200 ms
for broadband and monochromatic
frames, respectively. The two 12-bit CCD cameras (Berrilli et al. 1997)
are binned to
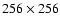 pixels. The Field of View (FoV) is
pixels. The Field of View (FoV) is
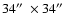 and the final pixel
size, for the binned images, was
and the final pixel
size, for the binned images, was
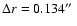 .
Seeing conditions and telescope set-up
limited the spatial resolution to
.
Seeing conditions and telescope set-up
limited the spatial resolution to
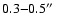 for broad-band images. The time interval between
two successive images and two successive spectral series was 2.5 s and 75 s respectively.
for broad-band images. The time interval between
two successive images and two successive spectral series was 2.5 s and 75 s respectively.
A
sub-array of approx.
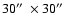 made up the final image series after the
assessment for dark current, flat field, image motion, and tracking loss of the telescope. In
this work we refer to 608 broadband frames that correspond to the conclusive 40-min sequence.
In order to reduce the noise and take into account the instrumental profile, we applied a Wiener
filter (Hunt 1984) to broadband images. We assumed a simple gaussian PSF (FWHM = 0.4
made up the final image series after the
assessment for dark current, flat field, image motion, and tracking loss of the telescope. In
this work we refer to 608 broadband frames that correspond to the conclusive 40-min sequence.
In order to reduce the noise and take into account the instrumental profile, we applied a Wiener
filter (Hunt 1984) to broadband images. We assumed a simple gaussian PSF (FWHM = 0.4
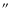 ,
comparable to the spatial resolution of the observations) and a S/N ratio equal to 15, which was
found to represent a good compromise between the level of restoration and the noise
amplification.
,
comparable to the spatial resolution of the observations) and a S/N ratio equal to 15, which was
found to represent a good compromise between the level of restoration and the noise
amplification.
The observations from the DST consist of a sequence of broadband images acquired on October 16,
1996 (from 14:30 UT to about 16:30 UT). Granulation frames were imaged
through an interference
filter at 550 nm, with 10 nm FWHM. The images were
recorded with a Videk 8-bit camera,
1360 1036 pixels, equipped with an
automatic frame selection system. Within an interval
of about 2 s, the best image among 12, i.e. the one with the highest rms value, was
retained and read by the camera. Each of the
images was acquired with an exposure time of 8 ms.
The total interval between successive images was 4.7 s.
A sub-portion of 1024
1036 pixels, equipped with an
automatic frame selection system. Within an interval
of about 2 s, the best image among 12, i.e. the one with the highest rms value, was
retained and read by the camera. Each of the
images was acquired with an exposure time of 8 ms.
The total interval between successive images was 4.7 s.
A sub-portion of 1024 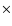 1024 pixels made up the final images. The image scale was set at 0.123 arcsec/pixel (
1024 pixels made up the final images. The image scale was set at 0.123 arcsec/pixel (
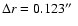 ), for a total field of view of about
), for a total field of view of about
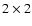 arcmin. Seeing conditions were excellent, and
the use of the DST granulation tracker (Rimmele et al. 1991) allowed a further improvement of
the image stability. For a great part of the sequence, the images are nearly diffraction limited (0.19
arcsec for the DST). After the standard dark current and flat field corrections, a
destretching algorithm was applied to remove the atmospheric distortion in the white light images. More
details can be found in Cauzzi et al. (1998). The final dataset covers a period of 1h 20m
(512 images) with a time resolution of 9.4 s.
arcmin. Seeing conditions were excellent, and
the use of the DST granulation tracker (Rimmele et al. 1991) allowed a further improvement of
the image stability. For a great part of the sequence, the images are nearly diffraction limited (0.19
arcsec for the DST). After the standard dark current and flat field corrections, a
destretching algorithm was applied to remove the atmospheric distortion in the white light images. More
details can be found in Cauzzi et al. (1998). The final dataset covers a period of 1h 20m
(512 images) with a time resolution of 9.4 s.
As shown by e.g., Title et al. (1989), the 5-min oscillations must be removed from the
intensity images before analyzing the granulation pattern. We hence applied a 3-dimensional
Fourier filter in the 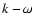 domain that removed all Fourier components with
domain that removed all Fourier components with
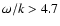 km s-1 and
km s-1 and
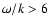 km s-1, for DST and THEMIS observations,
respectively.
km s-1, for DST and THEMIS observations,
respectively.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F6.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg51.gif) |
Figure 6:
The THEMIS average intensity (left panel) and rms (right panel) field as
obtained by the 40 min time-series. The image size is 
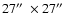 as resulting after
as resulting after 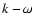 filtering.
filtering. |
In order to investigate the occurrence of a quasi-regular structure and of persistence in the
photospheric intensity fields we have time-averaged the granulation series over the entire
observing periods to recover the mean granulation pattern. In
Figs. 6 and 7 we report the average intensity fields along with the
corresponding rms intensity field as evaluated by the THEMIS and DST observations, respectively. As shown
in several studies (Getling & Brandt 2002; Baudin et al 1997), the resulting averaged
fields are not smeared out, showing, conversely, still persistent granular-like patterns. Moreover, also
the rms fields are also strongly structured, showing the occurrence of localized sites of fluctuations. We
postpone the study of these features to a future work.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F7.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg52.gif) |
Figure 7:
The DST average intensity (left panel) and rms (right panel)
field as obtained by the 90 min time-series. The image size is a portion
of 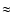
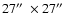 of the original image.
of the original image. |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{H3893F8.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg53.gif) |
Figure 8:
The binarized images of THEMIS (left panel) and DST (right panel) average
intensity field reported in Fig. 6 and 7. Images size is
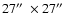 for convenience.
for convenience. |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{H3893F9.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg54.gif) |
Figure 9:
The normalised information entropy H' at different times for the
THEMIS binarized intensity fields. |
On single snapshots and the average images of the intensity fields the compact solar structures have been
extracted using a numerical binarization procedure based on a dynamical thresholding technique as
described in Berrilli et al. (1998, 2002). In more detail, the dynamical threshold
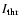 depends on the pixel position and on the statistical properties of a moving box centred
on the selected pixel according to the following expression:
depends on the pixel position and on the statistical properties of a moving box centred
on the selected pixel according to the following expression:
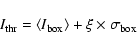 |
(9) |
where the
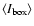 and
and
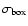 are, respectively, the intensity
average and the fluctuation rms in the moving box, and
are, respectively, the intensity
average and the fluctuation rms in the moving box, and 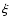 is a parameter. The choice of the moving box
size
is a parameter. The choice of the moving box
size
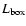 and of the
and of the 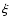 parameter has been accomplished by optimizing the area and the
number of extracted structures in the
parameter has been accomplished by optimizing the area and the
number of extracted structures in the
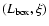 parameter space. The used optimal values
are
parameter space. The used optimal values
are
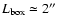 and
and 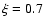 .
Although the used binarization procedure is not
optimized in order to extract the correct shape and dimension of solar granular structures as in
Bovelet & Wiehr (2001), the effects on the normalised information entropy H'(r) results are
negligible as discussed in Appendix A, being limited only to a slight shift of the first peak
position and to the absolute value of H'(r) maxima.
.
Although the used binarization procedure is not
optimized in order to extract the correct shape and dimension of solar granular structures as in
Bovelet & Wiehr (2001), the effects on the normalised information entropy H'(r) results are
negligible as discussed in Appendix A, being limited only to a slight shift of the first peak
position and to the absolute value of H'(r) maxima.
In Fig. 8 we report the binarized image relative to the averaged intensity field of
THEMIS and DST time series. From a comparative look at these binarized images we may note a difference in
the average dimension of the extracted granular structures, as also confirmed by the area coverage of the
structures which is 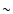 14% and
14% and 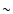 21% for THEMIS and DST images, respectively. We believe that
a possible explanation of the observed difference would be the different time interval
over which the averaging procedure is performed (
21% for THEMIS and DST images, respectively. We believe that
a possible explanation of the observed difference would be the different time interval
over which the averaging procedure is performed (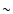 40 mn and
40 mn and 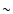 1 h 20 mn
for THEMIS and DST, respectively) which tends to smear the structures.
1 h 20 mn
for THEMIS and DST, respectively) which tends to smear the structures.
In this section we will show and discuss the results of information
entropy analysis on broadband
THEMIS and DST observations. We underline that for THEMIS observations in conjunction with broadband
images we have also collected spectral images by which an analysis similar to the one described in this
work can be applied to velocity fields at different photospheric heights. This will be the object of a
second paper in preparation at the moment.
In passing, we want to remark that in order to
compare the results coming from the two different observational campaigns we have limited our analysis to
the range of scales less than 10 Mm. This scale which corresponds to about half of the linear size
of THEMIS images, has been set in order to have a good statistics as previously discussed in Sect. 2. We
postpone the investigation of larger scales and the topology at these scales to a future work.
The first step of our approach to the possible existence of a topological ordering in the granulation
field is to investigate the behaviour of the normalised information entropy measure in single snapshots of
the granulation field. In order to do this we have selected a subset of 32 images with the highest image
quality among THEMIS observation. Each image is the best one in a subset of 9 images. The subsets have
been chosen to be timely separated by 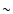 1 min 15 s.
1 min 15 s.
In Fig. 9 we report the normalised information entropy H'(r) for a set of THEMIS binarized
intensity fields at different times. In all the plots the behaviour of H'(r) as a function of the
box-scale r is characterized by a pronounced peak located at the scale 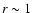 Mm. At larger scales
H'(r) displays a non-monotonous trend with the box-dimension r, showing secondary maxima that
evolve with time. As stated by Van Siclen (1997), H'(r) values larger than
zero are related with clustering effects. Thus, the location of the first peak of H'(r) must be read as
the consequence of the clustering effect of black pixels related to the granules. In other words, this
characteristic scale of
Mm. At larger scales
H'(r) displays a non-monotonous trend with the box-dimension r, showing secondary maxima that
evolve with time. As stated by Van Siclen (1997), H'(r) values larger than
zero are related with clustering effects. Thus, the location of the first peak of H'(r) must be read as
the consequence of the clustering effect of black pixels related to the granules. In other words, this
characteristic scale of 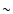 1 Mm represents an indirect measure of the granule typical size.
Furthermore, the presence of secondary maxima is the evidence of clustering effects of granular structures,
i.e. of clusters of granules. Similar results are recovered in the case of DST observations (data not shown here).
1 Mm represents an indirect measure of the granule typical size.
Furthermore, the presence of secondary maxima is the evidence of clustering effects of granular structures,
i.e. of clusters of granules. Similar results are recovered in the case of DST observations (data not shown here).
In order to get information on the possible existence of an average topological ordering (i.e. the
existence of an average temporal-spatial correlation of the granule positions) we have applied to
the H'(r) plots relative to all the selected set of images, the approach described in Sect. 2 to
decompose H'(r) in a superposition of contributions. The decomposition is accomplished by a nonlinear
best fit procedure (Levemberg-Marquardt algorithm) of the H'(r) using Eq. (7) with k=5. The
optimal number n of contribution functions was determined by analysing the trend of the reduced
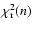 as a function of the number of contributions. Figure 10 shows the behaviour of the
quantity
as a function of the number of contributions. Figure 10 shows the behaviour of the
quantity
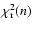 .
Larger numbers of contributions do not, indeed, reduce
.
Larger numbers of contributions do not, indeed, reduce 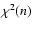 .
Figure 11 shows an example of such a decomposition of H'(r) using Eq. (7) for two
snapshots of THEMIS and DST observations. This decomposition has been applied to all the 32 selected
images and to a subset of DST observations, consisting of 64 images timely separated by an interval of
.
Figure 11 shows an example of such a decomposition of H'(r) using Eq. (7) for two
snapshots of THEMIS and DST observations. This decomposition has been applied to all the 32 selected
images and to a subset of DST observations, consisting of 64 images timely separated by an interval of
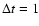 mn 25 s. In Fig. 12 it is shown the behaviour of the peak positions as a
function of time in the case of THEMIS observations (upper panel) and DST ones (lower panel).
mn 25 s. In Fig. 12 it is shown the behaviour of the peak positions as a
function of time in the case of THEMIS observations (upper panel) and DST ones (lower panel).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F10.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg67.gif) |
Figure 10:
The behaviour of the reduced
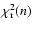 versus the number n of contributions
in the case of THEMIS H'(r) decomposition. The dashed line is an eye guide.
versus the number n of contributions
in the case of THEMIS H'(r) decomposition. The dashed line is an eye guide. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F11.eps}\par\includegraphics[width=8.8cm,clip]{H3893F12.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg68.gif) |
Figure 11:
The decomposition of the normalised information entropy H' for two images in the case
of THEMIS (upper panel) and DST (lower panel), respectively. Solid line is the best fit using
Eq. (7). The dashed lines show the single contributions. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F13.eps}\par\includegraphics[width=8.8cm,clip]{H3893F14.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg69.gif) |
Figure 12:
The behaviour of the position of the contributions of the H'(r) decomposition for
THEMIS (upper panel) and DST (lower panel), respectively. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F15.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg70.gif) |
Figure 13:
The average positions of the peaks of the H'(r) decompositions on single images for
THEMIS (black circles) and DST (empty circles) observations. Error bar represents the standard deviation.
The solid and dashed lines are linear best fits using the expression Eq. (8) of Sect. 2. |
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{H3893F16.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg71.gif) |
Figure 14:
The persistency pattern for the granulation field as evaluated from DST binarized
images. The upper panel shows a 3-d view of this pattern where the multipeaked structure is clearly
evident. The lower panel shows a 2-d view of the same persistence pattern where only the part of the
signal that exceeds the RMS value is shown. |
While the position of the first peak is constant with time, the positions of the other peaks fluctuate
with time. First of all, we remark that these temporal-fluctuations do not show any periodicity
and do not correlate with the quality images as described by the contrast. Moreover, we can identify some
time intervals when the secondary aggregations of the structures are modified in the direction of an
expansion of the overall arrangement of the granules (see for example the time interval from 12 mn
to 20 mn in THEMIS observations). Due to the time duration of this effect we exclude an
atmospheric origin and believe that this is due to the dynamics of the granulation fields.
We name this
behaviour dynamic topological deformation, meaning the occurrence of some plastic
deformations of
the overall topology.
As a matter of fact, if the position of secondary maxima would be fixed in time, we
should think about the presence of a sort of rigid
topology that would not change the shape of H'(r).
Conversely, this result suggests that we are in the case of a deformable topology similar to that of a fluid/amorphous system.
Starting from these results on single images we have evaluated the average positions of the secondary
maxima. Averaging procedure was performed over time by considering only those values of the peak positions
that fall inside the range
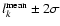 ,
where
,
where
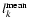 is the mean value evaluated
on all the data set and
is the mean value evaluated
on all the data set and 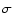 is the standard deviation.
In Fig. 13 we show the average position
is the standard deviation.
In Fig. 13 we show the average position
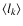 of the secondary peaks as a function
of the odd numbers. A linear relationship is found suggesting the existence of a characteristic scale l0that is the signature of a topological ordering in the mutual positions of the granular structures. When
the dependence of
of the secondary peaks as a function
of the odd numbers. A linear relationship is found suggesting the existence of a characteristic scale l0that is the signature of a topological ordering in the mutual positions of the granular structures. When
the dependence of
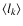 on the odd numbers is fitted using Eq. (8) we found
on the odd numbers is fitted using Eq. (8) we found
![$l_0 =
[1.69 \pm 0.07]$](/articles/aa/full/2003/18/aah3893/img76.gif) Mm and
Mm and
![$l_0 =[1.44 \pm 0.06]$](/articles/aa/full/2003/18/aah3893/img77.gif) Mm for THEMIS and DST, respectively. Let us
say some words on the meaning of this scale. Although this topological ordering scale l0
could be related to the average dimension of the convective cells (see the discussion in the next section),
this characteristic scale plays the same role of the lattice constant, being related with the presence
of a quasi-regular pattern in the intensity field. We remark that, to our knowledge, this result is the first
quantitative evidence of a spatial ordering in the granulation pattern. In passing we anticipate
that similar results have been found analysing velocity fields as observed in C I line at
Mm for THEMIS and DST, respectively. Let us
say some words on the meaning of this scale. Although this topological ordering scale l0
could be related to the average dimension of the convective cells (see the discussion in the next section),
this characteristic scale plays the same role of the lattice constant, being related with the presence
of a quasi-regular pattern in the intensity field. We remark that, to our knowledge, this result is the first
quantitative evidence of a spatial ordering in the granulation pattern. In passing we anticipate
that similar results have been found analysing velocity fields as observed in C I line at
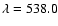 nm, which is representative of the deeper layers in the solar photosphere.
nm, which is representative of the deeper layers in the solar photosphere.
Another relevant aspect that can be investigated is the persistence of such a spatial topological
ordering. As a matter of fact, looking to the granular pattern evolution with time we can immediately
realize that granules tend to be born in the nearby sites of pre-existing granular structure. In order to
visualize this aspect of the granulation pattern evolution we have constructed an image as the sum of DST
images binarized following the procedure described in Sect. 3. Figure 14 shows a 3-d view of the
resulting image (upper panel) along with a 2-d view (lower panel). The existence of a multipeaked
structure of the resulting pattern from this image is a clear evidence of persistence in the granulation
intensity field. We emphasize two aspects related to this persistence in binarized images: i) the
persistent granular-like patterns reported in Figs. 6 and 7 are not due to
particular bright intensity structures; ii) we found more than 30 local regions (zero points in the image) that are never sites of a granule.
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{H3893F17.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg79.gif) |
Figure 15:
The evolution of the normalised information entropy H' by averaging DST images with
time. |
Figure 15 shows the evolution of the normalised information entropy H'(r) as evaluated
by averaging the DST images with time. These plots clearly shows a temporal evolution of the secondary
H'(r) maxima. The observed evolution could be related to the temporal emergence of structures and/or
pattern at scales usually associated with mesogranulation. Since its discovery, the spatial and
temporal characteristics related to mesogranulation have been difficult to determine accurately (Rieutord et al. 2000). Anyway, the typical spatial and temporal scales associated with mesogranulation
range within length scale between 3 Mm and 10 Mm and time scales between 30 min and 6 h. In order to get
some insight on mesogranulation from the normalised information entropy measure analysis we have
investigated the change of the H'(r) with averaging time at three different range of scales reported in
literature: 3.5-4.5 Mm (Lawrence et al. 2001), 4.0-7.0 Mm (Shine et al. 2000),
and
5.0-10.0 Mm (November et al. 1981).
In Fig. 16 we report the evolution of the H'(r) percentage contribution
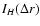 with averaging time
with averaging time 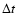 in the three above mentioned ranges of scales, as defined
according to the following expression:
in the three above mentioned ranges of scales, as defined
according to the following expression:
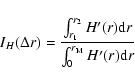 |
(10) |
where r1 and r2 are the extremes of the range of scales, and 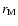 is the maximum length scale
here investigated (
is the maximum length scale
here investigated (
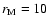 Mm). This figure allows us to trace in time the statistical weight of
the three selected ranges of scales. In detail, the
Mm). This figure allows us to trace in time the statistical weight of
the three selected ranges of scales. In detail, the
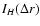 at
5.0-10.0 Mm shows a clear
evolution with averaging time, the information entropy percentage contribution at the other two ranges of
scales is nearly constant. This result suggests the existence of a spatial coherence with a
characteristic time scale of
at
5.0-10.0 Mm shows a clear
evolution with averaging time, the information entropy percentage contribution at the other two ranges of
scales is nearly constant. This result suggests the existence of a spatial coherence with a
characteristic time scale of 
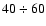 min at scales larger than 5.0 Mm.
min at scales larger than 5.0 Mm.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{H3893F18.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg85.gif) |
Figure 16:
Percetange contribution to the overall information entropy H'(r) in three different
range of scales 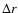 as a function of averaging time
as a function of averaging time 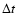 . . |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{H3893F19.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg86.gif) |
Figure 17:
The normalised information entropy H' (empty circles) for the DST binarized average
intensity field. Solid line is the best fit using Eq. (7) with k=6. The dotted lines show the single contributions. Only contributions with maxima inside 10 Mm are shown for convenience. |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{H3893F20.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg87.gif) |
Figure 18:
The peak positions of the H'(r) contributions versus odd numbers for THEMIS (solid
circles) and DST (empty circles) average intensity fileds. The solid and dashed lines are linear fit for THEMIS and DST, respectively. |
Figure 17 shows the H'(r) along with its decomposition for the DST binarized average intensity
field. Similar results have been found in the case of THEMIS average intensity field (data not shown).
We have decomposed the H'(r) in a superposition of contributions following the same procedure applied for
single images. Figure 18 reports the positions lk of the contribution peaks vs. odd numbers for
both DST and THEMIS results. A linear relationship is recovered in both cases, and using Eq. (8) we
can define two characteristic length scales:
![$l_0 = [1.55 \pm 0.03]$](/articles/aa/full/2003/18/aah3893/img88.gif) Mm and
Mm and
![$l_0 = [1.53 \pm 0.05]$](/articles/aa/full/2003/18/aah3893/img89.gif) Mm for
DST and THEMIS, respectively. These values do not meaningfully differ from the topological ordering
scale found on single images, suggesting that topological ordering is an intrinsic feature of the convective pattern as observed by means of intensity fields.
Mm for
DST and THEMIS, respectively. These values do not meaningfully differ from the topological ordering
scale found on single images, suggesting that topological ordering is an intrinsic feature of the convective pattern as observed by means of intensity fields.
In this work, we have tackled the highly debated topic of regular structures in the solar
photosphere (Getling & Brandt 2002; Rast 2002) by means of information theory. In
detail using the normalised information entropy measure, as defined by Van Siclen (1997),
we have quantitatively investigated the existence of a hidden ordering in the topology of the granular structures. Our findings may be summarized as follows:
- 1.
- The normalised information entropy measure H'(r) analysis shows a pronounced peak at
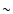 1 Mm both in average and single images. This peak is related to the average
length scale of the granular structures, as obtained by the numerical binarization procedure, and voids among granules.
1 Mm both in average and single images. This peak is related to the average
length scale of the granular structures, as obtained by the numerical binarization procedure, and voids among granules.
- 2.
- Other relevant scales emerge in the H'(r) as secondary maxima. These scales are the
signature of secondary clustering effects due to a non-random distribution of the granular structures.
- 3.
- The decomposition of H'(r) reveals the existence of a hidden ordering topology in both single and
average granular patterns which allows us to define an average topological ordering length scale
![$l_0 =
[1.55 \pm 0.10]$](/articles/aa/full/2003/18/aah3893/img90.gif) Mm. While the
Mm. While the 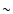 1 Mm scale shows the primary contribution due to granules, the
1 Mm scale shows the primary contribution due to granules, the
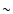 1.55 Mm scale contains positional information of individual cells that recognise their position with
respect to their partners. As a matter of fact, the scale we found
characterizes the system as ordered and
defines a correlation between parts of the system (i.e. photospheric flows) as it occurs in the case of a crystal lattice.
1.55 Mm scale contains positional information of individual cells that recognise their position with
respect to their partners. As a matter of fact, the scale we found
characterizes the system as ordered and
defines a correlation between parts of the system (i.e. photospheric flows) as it occurs in the case of a crystal lattice.
- 4.
- The percentage contribution
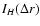 to H'(r) in the range
to H'(r) in the range
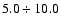 Mm shows
an evolution with averaging time-interval. This result suggests the existence of a spatial coherence with a
characteristic time scale of
Mm shows
an evolution with averaging time-interval. This result suggests the existence of a spatial coherence with a
characteristic time scale of 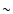
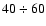 min on typical scales associated with mesogranulation.
min on typical scales associated with mesogranulation.
The picture that emerges from our analysis implies the presence of space-time ordering in the
topology of the solar convection pattern.
The space ordering, present in both single and average images,
suggests the occurrence of time persistence in the origin points for granules. We remark that the observed
persistence is also confirmed by the averaging procedure of the binarized images that eliminate the effects
of particularly bright structures. Moreover, conversely to what stated by Getling
& Brandt (2002) the observed regularity on the granulation pattern is even revealed in single
images. In other words, also the single images reveal the presence of a ordered topology, while the time average images point out the spatial persistence of this ordered topology.
Concerning the emergence of this topological ordering, we believe that the existence of a quasi-regular
pattern might be understood in the framework of a complex system of space-time coupled structures
with a characteristic size. Let us consider two different classes of random phenomena (Pagels
1985): i) the rain falling on a sand beach, ii) the nesting of a seabird colony on a cliff.
In the first phenomenon no regular pattern is observed either instantaneously or with increasing
time due to the lack of a space-time coupling among the falling raindrops and to the total random
nature of the process. This leads to a flat pattern without spatial ordering and time persistence.
Conversely, looking at the nests of a seabird colony we may recognize a sort of ordering and
persistence in the nesting pattern. In this case, the process requires certain constraints on the
minimum distance between two nests (the pecking distance), which is equivalent to the
existence of a spatial correlation length. The emergence of a structured pattern in the nesting phenomenon
is the signature of complexity and self-organization in such a random system consisting of interacting
elementary subsystems.
In the case of solar granulation pattern, we retain that this complex system may be considered to some
extent equivalent to the nesting process, where the role of the average distance between two nests is
played by typical correlation scale between convective matter flows. Here, the self-organization, which
comes out from the inherent spatial symmetry breaking due to the convective process, induces a spatial
ordering. Our analysis reveals the existence of such a spatial ordering characterized by a length scale
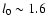 Mm. The emerging picture looks similar to our previous findings on the scaling features of
the velocity fields (Consolini et al. 1999a,1999b).
Mm. The emerging picture looks similar to our previous findings on the scaling features of
the velocity fields (Consolini et al. 1999a,1999b).
In conclusion, our analysis on the topology of the granulation pattern, as extracted using the binarization
procedure on intensity photospheric fields, suggests the existence of a certain amount of regularity in the
solar convection pattern. However, a definitive answer on the existence of a regular convective
pattern requires the investigation of velocity fields that better describe the matter flow topology. We
recall that intensity field, being related to the temperature field (i.e. to the advected scalar
quantity), might give a non-exhaustive view of the underlying convective field. A detailed analysis of the
velocity field pattern topology will be presented in a forthcoming paper.
Acknowledgements
We wish to thank the THEMIS staff for the efficient support in the observations and in
particular we are grateful to C. Briand, G. Ceppatelli and G. Mainella. The authors are
indebted to NSO/SP-DST staff for the telescope time allocation and the invaluable help during the
observations. We would like also to thank T. Straus and G. Cauzzi for providing DST images and
k- filtering. Special thanks to P.N. Brandt and M.P. Rast for useful discussions. This work was
partially supported by the Italian National Research Council (CNR) grant Agenzia2000 CNRC0084C4.
filtering. Special thanks to P.N. Brandt and M.P. Rast for useful discussions. This work was
partially supported by the Italian National Research Council (CNR) grant Agenzia2000 CNRC0084C4.
This work is partially based on observations made with THEMIS-CNRS/INSU-CNR operated on the island of
Tenerife by THEMIS S.L. in the Spanish Observatorio del Teide of the Instituto de Astrofisica de
Canarias.
In this Appendix we present the results of information entropy analysis on some meaningful
simulated periodic and non-periodic patterns. All the patterns here considered are 200 pixels
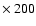 pixels two-level images. In all these cases the evaluation of information entropy measure has been
limited to the range
pixels two-level images. In all these cases the evaluation of information entropy measure has been
limited to the range
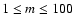 for statistical meaning.
for statistical meaning.
In Fig. A.1 we report two periodic
configurations: a square periodic pattern with a lattice length
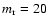 pixels
(left panel), and a
triangular periodic pattern with a lattice length
pixels
(left panel), and a
triangular periodic pattern with a lattice length
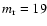 pixels (right panel). In passing we note
that the triangular periodic pattern derives from a hexagonal regular tessellation of the plane where the
structures lie in the centre of hexagons. The behaviour of H'(m) for the two patterns is
shown in Fig. A.2. It is evident how the normalised information entropy H'(m) is able to
capture the periodicity of the lattice. In detail, as argued by Van Siclen (1997) while the
minima reveal the underlying periodicity, as sampled by the squared
pixels (right panel). In passing we note
that the triangular periodic pattern derives from a hexagonal regular tessellation of the plane where the
structures lie in the centre of hexagons. The behaviour of H'(m) for the two patterns is
shown in Fig. A.2. It is evident how the normalised information entropy H'(m) is able to
capture the periodicity of the lattice. In detail, as argued by Van Siclen (1997) while the
minima reveal the underlying periodicity, as sampled by the squared
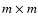 sliding box, the maxima
are also related with the typical length scale of the regions devoid of black pixels. Indeed, in this
analysis a region devoid of black pixels must also be considered as a structure giving a
nonvanishing contribution to the information entropy.
sliding box, the maxima
are also related with the typical length scale of the regions devoid of black pixels. Indeed, in this
analysis a region devoid of black pixels must also be considered as a structure giving a
nonvanishing contribution to the information entropy.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F21.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg97.gif) |
Figure A.1:
Two periodic patterns of structures: a square lattice (left panel) and a
triangular lattice (right panel). |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F22.eps} \includegraphics[width=8.8cm,clip]{H3893F23.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg98.gif) |
Figure A.2:
The normalised information entropy H'(m) of the two patterns reported in
Fig. A.1. Upper and lower panel refer to the square and triangular lattice, respectively. |
In the following we report the results on different types of random patterns in order to clarify how
randomness affects the information entropy measure analysis. In detail, we investigate the case of a random
distribution of structures on a regular pattern, and of a total randomness. We remark that in
order to compare the results coming from these different patterns we have also fixed the number of
structures in each pattern to be exactly 100.
Figure A.3 shows two different pseudorandom distributions on
regular patterns. In the first case
(left panel) we have a regular triangular pattern with structures of random shapes located on the lattice
sites. The second case refers to the same pseudorandom pattern shown in Fig. 3, but where
the structures have random shapes. The lattice constants of the two hidden regular patterns are
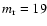 pixels and
pixels and
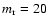 pixels for the triangular and square patterns, respectively. The
results of the analysis of the normalised information entropy measure on the two patterns are reported in
Fig. A.4. We note that the different degree of randomness of the two patterns reflects on the different behaviour of
H'(m): a higher randomness corresponds to a less evidence of the secondary maxima.
pixels for the triangular and square patterns, respectively. The
results of the analysis of the normalised information entropy measure on the two patterns are reported in
Fig. A.4. We note that the different degree of randomness of the two patterns reflects on the different behaviour of
H'(m): a higher randomness corresponds to a less evidence of the secondary maxima.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F24.eps} \end{figure}](/articles/aa/full/2003/18/aah3893/Timg99.gif) |
Figure A.3:
Two periodic patterns of structures: a square lattice (left panel) and a
triangular lattice (right panel). |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F25.eps} \includegraphics[width=8.8cm,clip]{H3893F26.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg100.gif) |
Figure A.4:
The H'(m) behaviour for the two random patterns reported in Fig. A.3. Upper
and lower panels refer to triangular and square lattice. Solid line is the best fit of H' using
Eq. (7). Dashed lines are the single contributions. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F27.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg101.gif) |
Figure A.5:
The trends of the peak positions versus the odd numbers for the two decompositions shown
in Fig. A.4. Empty and solid circles indicate the peak positions for the triangular and square
lattice, respectively. Solid and dashed lines are linear best fits. |
In applying the same procedure discussed in Sect. 2, H'(m) for the above
random patterns has been
decomposed in a superposition of a set of contribution functions. The
decompositions are also shown in
Fig. A.4. The linear relationship between the peak positions of the contributions and the odd
numbers (Fig. A.5) allows us to extract the underlined periodicity of the patterns and to
derive the lattice characteristic lengths:
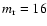 pixels (triangular lattice) and
pixels (triangular lattice) and
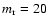 pixels (square lattice). The extracted
pixels (square lattice). The extracted
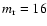 pixels characteristic length for the triangular
lattice exactly corresponds to the lattice constant of
pixels characteristic length for the triangular
lattice exactly corresponds to the lattice constant of
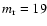 pixels when the triangular pattern is
investigated using a square moving box. As a matter of fact the extracted value results from the projection
of the lattice vector on the orthogonal reference system of the moving box.
pixels when the triangular pattern is
investigated using a square moving box. As a matter of fact the extracted value results from the projection
of the lattice vector on the orthogonal reference system of the moving box.
![\begin{figure}
\par\includegraphics[width=4.4cm,clip]{H3893F28.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg103.gif) |
Figure A.6:
A snapshot of a pseudorandom pattern of non-overlapping structures. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F29.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg104.gif) |
Figure A.7:
H'(m) for the single snapshot reported in Fig. A.6 (solid circles) and the set
of 1000 pseudorandom patterns (empty circles). |
Finally, we have studied the behaviour of H'(m) in the case of a pseudorandom pattern consisting of a set
of random shapes pseudorandomly distributed (see Fig. A.6). The only constraint in the
construction of this image is the requirement that the structures do not overlap each other. That
limits the maximum size of the structures. Moreover, we have also studied the H'(m) averaged on a
set of 1000 pseudorandom patterns generated as described above. Figure A.7 shows
H'(m) for a single snapshot and for a set of 1000 pseudorandom patterns. Both single and average H'(m)monotonously increase to the average scale of the empty zone that is about 19-20 pixels. We
remember that information is also contained in the empty zones. Moreover above this scale H'(m) does not
display any evident secondary maxima as a consequence of the absence of any regularities, showing a
totally flat trend for the average information entropy. The flat behaviour at larger scales reflects the
non-increasing content of information at scales larger than the ones relative to the structures.
-
Andraud, C., Beghdadi, A., & Lafait, J. 1994, Physica A, 207, 208
-
Andraud, C., Beghdadi, A., Haslund, E., et al. 1997, Physica A, 235, 307
NASA ADS
-
Baudin, F., Molowny-Horas, R., & Koutchmy, S. 1997, A&A, 326, 842
NASA ADS
-
Beck, C., & Schlögl, F. 1993, Thermodynamics of chaotic systems (Cambridge, UK: Cambridge
University Press)
-
Berrilli, F., Caccin, B., Cantarano S., et al. 1997, Il Nuovo Cimento, 20, 297
-
Berrilli, F., Florio, A., & Ermolli, I. 1998, Sol. Phys., 180, 29
NASA ADS
-
Berrilli, F., Consolini, G., Pietropaolo, E., et al. 2002, A&A, 381, 253
NASA ADS
-
Bovelet, B., & Wiehr, E. 2001, Sol. Phys., 201, 13
-
Cattaneo, F., Lenz, D., & Weiss, N. 2001, ApJ, 563, L91
NASA ADS
-
Cauzzi, G., Consolini, G., Berrilli, F., et al. 1998, Memorie SAIt, 69, 647
NASA ADS
-
Cavallini, F. 1998, A&A, 128, 589
-
Consolini, G., Carbone, V., Berrilli, F., et al. 1999a, A&A, 344, L33
NASA ADS
-
Consolini, G., Berrilli, F., Pietropaolo, E., et al. 1999b, in Magnetic Fields and Solar Processes, ed. A. Wilson, ESA SP-488, 209
-
Frisch, U. 1995, Turbulence - The Legacy of A.N. Kolmogorov (Cambridge: Cambridge University
Press)
-
Getling, A. V., & Brandt, P. N. 2002, A&A, 382, L5
NASA ADS
-
Hoekzema, N. M., Brandt, P. N., & Rutten, R. J. 1998, A&A, 333, 322
NASA ADS
-
Hunt, B. R. 1984, Image Restoration in Digital Image Processing Techniques (Academic Press, Inc.)
-
Lawrence, J. K., Cadavid, A. C., & Ruzmaikin, A. A. 1999, ApJ, 513, 506
NASA ADS
-
Lawrence, J. K., Cadavid, A. C., & Ruzmaikin, A. A. 2001, Sol. Phys., 202, 27
NASA ADS
-
Legrenzi, P. 2002, Prima lezione di scienze cognitive (Editori Laterza, Bari)
-
Müller, D. A. N., Steiner, O., Schlichenmaier, R., et al. 2001, Sol. Phys., 203, 211
NASA ADS
-
Nordlund, Å., Spruit, H. C., Ludwig, H.-G., et al. 1997, A&A, 328, 229
NASA ADS
-
November, L. J., Toomre, J., Gebbie, K. B., et al. 1981, ApJ, 245, L123
NASA ADS
-
Pagels, H. R. 1985, Perfect Symmetry - The Search of the Beginning of Time (New York: Bantam
Books)
-
Ploner, S. R. O., Solanki, S. K., & Gadun, A. S. 2000, A&A, 356, 1050
NASA ADS
-
Rast, M. P. 1999, in High Resolution Solar Physics: Theory, Observations and Techniques, ed. T. R. Rimmele, K. S. Balasubramaniam, & R. R. Radick, p. 443
-
Rast, M. P. 2002, A&A, 392, L13
NASA ADS
-
Rieutord, M., Roudier, T., Malherbe, et al. 2000, A&A, 357, 1063
NASA ADS
-
Rimmele, Th., von der Luehe, O., Wiborg, P. H., et al. 1991, SPIE, 1542, 186
NASA ADS
-
Roudier, Th., Malherbe, J. M., November, L., et al. 1997, A&A, 320, 605
NASA ADS
-
Shannon, C. E., & Weaver, W. 1959, The mathematical theory of communication (Urbana: University of Illinois)
-
Shine, R. A., Simon, G. W., & Hurlburt, N. E. 2000, Sol. Phys., 193, 313
NASA ADS
-
Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914
NASA ADS
-
Spruit, H. C., Nordlund, Å., & Title, A. M. 1990, ARA&A, 28, 263
NASA ADS
-
Starck, J.-L., Murtagh, F., & Bijaoui, A. 1998, Image Processing and Data Analysis. The Multiscale Approach (Cambridge: Cambridge University Press)
-
Title, A. M., Tarbell, T. D., Topka, S. H., et al. 1989, ApJ, 336, 475
NASA ADS
-
Van Siclen, C. Dew. 1997, Phys. Rev. E, 56, 5211
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H3893F1.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg14.gif)
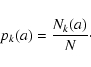
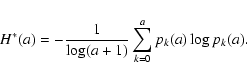
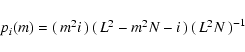
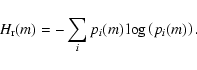
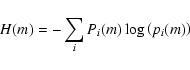
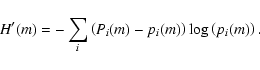
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H3893F2.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg31.gif)
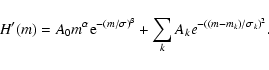
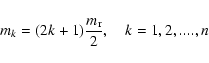
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F4.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg38.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F5.eps} \end{figure}](/articles/aa/full/2003/18/aah3893/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{H3893F9.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg54.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F10.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F11.eps}\par\includegraphics[width=8.8cm,clip]{H3893F12.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg68.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F13.eps}\par\includegraphics[width=8.8cm,clip]{H3893F14.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F15.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{H3893F16.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{H3893F17.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg79.gif)
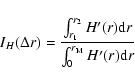
![\begin{figure}
\includegraphics[width=8.8cm,clip]{H3893F18.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg85.gif)
![\begin{figure}
\includegraphics[width=8.8cm,clip]{H3893F19.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg86.gif)
![\begin{figure}
\includegraphics[width=8.8cm,clip]{H3893F20.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F22.eps} \includegraphics[width=8.8cm,clip]{H3893F23.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg98.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F25.eps} \includegraphics[width=8.8cm,clip]{H3893F26.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F27.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=4.4cm,clip]{H3893F28.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg103.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3893F29.eps}\end{figure}](/articles/aa/full/2003/18/aah3893/Timg104.gif)