A&A 402, L35-L38 (2003)
DOI: 10.1051/0004-6361:20030336
M. Olberg1 - U. Frisk2 - A. Lecacheux3 - A. O. H. Olofsson1 - P. Baron3 - P. Bergman1 - G. Florin2 - Å. Hjalmarson1 - B. Larsson4 - D. Murtagh5 - G. Olofsson4 - L. Pagani6 - Aa. Sandqvist4 - D. Teyssier7 - S. A. Torchinsky8 - K. Volk9
1 - Onsala Space Observatory, 439 92 Onsala, Sweden
2 -
Swedish Space Corporation, PO Box 4207, 171 04 Solna, Sweden
3 -
LESIA, Observatoire de Paris, Section de Meudon, 5 place Jules
Janssen, 92195 Meudon Cedex, France
4 -
Stockholm Observatory, SCFAB, Roslagstullsbacken 21, 106 91
Stockholm, Sweden
5 -
Global Environmental Measurements Group, Chalmers University of
Technology, 412 96 Göteborg, Sweden
6 -
LERMA & FRE 2460 du CNRS, Observatoire de Paris, 61 Av. de l'Observatoire,
75140 Paris, France
7 -
SRON, Postbus 800, 9700 AV Groningen, The Netherlands
8 -
Canadian Space Agency, St-Hubert, J3Y 8Y9, Québec, Canada
-
Department of Physics and Astronomy, University of Calgary, Calgary,
ABT 2N 1N4, Canada
Received 2 December 2002 / Accepted 25 January 2003
Abstract
The radiometer on-board the Odin satellite comprises four different
sub-mm receivers covering the 486-581 GHz frequency range and one
fixed frequency 119 GHz receiver. Two auto-correlators and one
acousto-optical spectrometer serve as backends. This article gives an
overview over the processing of the data delivered by these instruments and
discusses calibration issues.
Key words: space vehicles: instruments - submillimeter - techniques: spectroscopic - telescopes
The calibration of radio observations from satellites differs in a number of aspects from that of ground-based observations. On the one hand the main difficulty for radio telescopes on ground, namely to properly account for the attenuation of the signal by the Earth's atmosphere, is no longer an issue. On the other hand the much more indirect operation of a satellite borne telescope has challenges of its own. The thermal and electrical environment of a satellite may cause receiver instabilities, which must be compensated. Whereas ground based systems may have relatively stable gain but changing system temperature due to unstable weather conditions, the Odin satellite shows the opposite behaviour: stable noise figures in spite of cyclic gain variations during one orbit.
Typically, an observing program is uploaded during passages above the
ground station and the processing needs to make sure that the
downloaded telemetry data is compatible with the intended observation.
Also, satellites normally lack the means to compensate in real-time
for Doppler effects introduced by the orbital motion of the satellite
around the Earth (
![]() ). As a consequence
short time integrations are performed, which are subsequently aligned on a
rest frequency scale by the processing software. This leads to high
data volumes with an immediate need for some kind of processing
pipeline. Failing instruments cannot be repaired, and instead the
processing needs to be adapted to new situations.
). As a consequence
short time integrations are performed, which are subsequently aligned on a
rest frequency scale by the processing software. This leads to high
data volumes with an immediate need for some kind of processing
pipeline. Failing instruments cannot be repaired, and instead the
processing needs to be adapted to new situations.
Odin is a sub-mm satellite with a dual mission: astronomy and aeronomy. Odin observing time is split evenly between these two disciplines: the search for mainly water and oxygen emission from astronomical objects (Hjalmarson et al. 2003) and observations of the Earth's atmosphere in order to map, the distribution of molecules relevant in the context of ozone depletion (Murtagh et al. 2002).
The satellite orbits the Earth in a sun-synchronous orbit at an
altitude of ![]()
![]() ,
passing the ground station at
Esrange in northern Sweden about fourteen times a day.
The 1.1 m offset Gregorian telescope has a beam width of
,
passing the ground station at
Esrange in northern Sweden about fourteen times a day.
The 1.1 m offset Gregorian telescope has a beam width of
![]() and
and
![]() at 500 GHz and 119 GHz, respectively. From Jupiter
observations we estimate a main beam efficiency of
at 500 GHz and 119 GHz, respectively. From Jupiter
observations we estimate a main beam efficiency of
![]() .
Pointing accuracy is better than
.
Pointing accuracy is better than
![]() .
.
The satellite is equipped with four sub-mm receivers. Table 1 lists their single sideband (SSB) tuning ranges. In addition a fixed frequency millimeter receiver covering the ground transition of molecular oxygen operates near 119 GHz. Typical single-sideband system temperatures are 3300 K and 600 K for the sub-mm and mm receivers, respectively.
The receivers form two groups, A1+A2 and B1+B2+C, where each group shares a common path through the beam optics. Consequently, in Dicke switching mode one group will receive its signal via the main beam when the other sees the reference signal, and vice versa. This design also implies, that in position switched mode only one group can be used at the same time.
Three spectrometers, one acousto-optical spectrometer and two auto-correlators of hybrid type can be connected to the receivers in a number of ways. In addition, signal combiners allow one correlator to be shared between two sub-mm receivers.
A 3-channel filter bank, slaved to one of the correlators, is used in aeronomy mode to monitor emission in the 119 GHz band in order to derive estimates of atmospheric temperature and pressure.
A block diagram showing the arrangements of receivers and spectrometers is presented in Frisk et al. (2003), who describe other technical aspects of the radiometer. The same diagram also outlines the main features of the beam optics.
| frontend | tuning | backend | band- | channel |
| range | width | spacing | ||
| GHz | MHz | MHz | ||
| 549 A1 | 541-558 | AOS | 1050 | 0.61 |
| 495 A2 | 486-504 | AC1/AC2 | 800 | 1.0 |
| 555 B1 | 547-564 | 400 | 0.5 | |
| 572 B2 | 563-581 | 200 | 0.25 | |
| 119 C | 118.75 | 100 | 0.125 |
The main observing mode is by switching against the cold sky, by means
of a chopper-wheel, between the main beam and an
unfocused sky beam of ![]() FWHM at all wavelengths. Integration times
per phase are between 1 and 10 s. An internal selection mirror
can choose between two possible directions of the sky beam, separated
by
FWHM at all wavelengths. Integration times
per phase are between 1 and 10 s. An internal selection mirror
can choose between two possible directions of the sky beam, separated
by ![]() .
The separation from the main beam amounts to
.
The separation from the main beam amounts to ![]() .
In astronomy mode the sky beam is chosen such that contamination
from solar system objects and the Galactic plane is avoided. In aeronomy, the
beam pointing away from the Earth is used.
.
In astronomy mode the sky beam is chosen such that contamination
from solar system objects and the Galactic plane is avoided. In aeronomy, the
beam pointing away from the Earth is used.
For calibration purposes the selection mirror may also direct the beam towards an internal load at ambient temperature.
Due to a sun constraint Odin's main beam is always within ![]() of the orbital plane, and for about one third of the orbit the
astronomical object will be occulted by the Earth (see
Fig. 1). This leaves about two thirds of the time, or
roughly 60 min per orbit, for target observations. During this
time the Doppler shift due to the satellite's motion will change from -7 km s-1 to +7 km s-1, which subsequently needs to be corrected for
as part of the on-ground data processing.
of the orbital plane, and for about one third of the orbit the
astronomical object will be occulted by the Earth (see
Fig. 1). This leaves about two thirds of the time, or
roughly 60 min per orbit, for target observations. During this
time the Doppler shift due to the satellite's motion will change from -7 km s-1 to +7 km s-1, which subsequently needs to be corrected for
as part of the on-ground data processing.
On entering and leaving the occulted part the telescope beam will pick up a signal from the terrestrial atmosphere, which can be used for accurate frequency calibration.
Figure 2 shows the mean intensity across all channels of one of the spectrometers during the course of one astronomy orbit of Dicke switched observations. Data from different beam directions (main beam, sky beam and internal load) are labelled. The typical gain variation due to a changing thermal environment during one orbit is clearly seen. Main beam data are at a higher level compared to cold sky due to thermal emission from a baffle.
It turns out that the slight imbalance between signal and reference phase introduces instabilities seen as low-level ripple in the spectrometer passbands. This ripple is stable in the IF band, and can be measured towards a blank region of the sky and subsequently be subtracted from target spectra. A figure showing the noise level at 119 GHz as function of time is available in Pagani et al. (2003).
In position switched observations the satellite is moved between target and off position about once per minute, while data readout still occurs every few seconds, to prevent deterioration of the frequency resolution due to Doppler effects. While this avoids the above mentioned ripple, the system is more sensitive to gain variations as switching is not as fast in this mode.
The calibration scheme is based on the assumption that the digital
value ci read out from channel i of a spectrometer and normalised
by division by integration time, is proportional to the observed
signal. The contributions to the signal are expressed as equivalent
Rayleigh-Jeans temperatures:
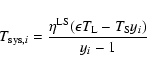 |
(3) |
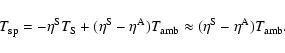 |
(6) |
The processing usually works with data from one orbit at a time, and typically goes through the following sequence:
A general description of correlators and acousto-optical spectrometers used in radio astronomy can be found in Rohlfs & Wilson (2000).
The two correlators on-board were built by the Swedish company Omnisys
and are of hybrid type, using up to
![]() MHz bands. Eight
correlator chips provide 96 lags each. The centre IF of each sub-band
is tuneable within a 500 MHz wide band in 1 MHz steps. The channel spacing
ranges from 125 kHz in 1-band mode to 1 MHz in 8-band
mode. The spectral resolution is twice the channel spacing due to the
applied Hanning smoothing.
MHz bands. Eight
correlator chips provide 96 lags each. The centre IF of each sub-band
is tuneable within a 500 MHz wide band in 1 MHz steps. The channel spacing
ranges from 125 kHz in 1-band mode to 1 MHz in 8-band
mode. The spectral resolution is twice the channel spacing due to the
applied Hanning smoothing.
The 3-level correlation scheme used here is extensively discussed in the
literature;
Kulkarni & Heiles (1980) use a relation known as Price's
theorem to arrive at the relation between the true correlation ![]() and the measured, modified correlation coefficients r at lag
and the measured, modified correlation coefficients r at lag ![]() .
For the case
c+ = -c- = c, where
.
For the case
c+ = -c- = c, where
![]() are
the threshold voltages divided by the standard deviation of the input
noise, this relation can be expressed as:
are
the threshold voltages divided by the standard deviation of the input
noise, this relation can be expressed as:
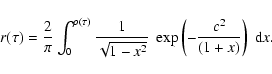 |
(7) |
The AOS was built by a consortium of three French laboratories: LAS (Marseille), CESR (Toulouse) and the Radio Astronomy Department of the Paris-Meudon Observatory (Lecacheux et al. 1998).
The photo detector is a 1754 pixels, linear CCD with 1728 usable frequency channels with a spectral resolution of 1.0 MHz. The CCD video output is read out every 5 ms and digitised over 12 bits, in order to keep the noise statistics of the signal unmodified over a dynamical range greater than 10 dB. A pre-adder delivers the sum of four consecutive readouts to the on-board micro computer, which performs the final double buffer integration in synchronism with the radiometer and antenna pointing information. The on-board micro computer also performs instrument monitoring and manages communication with the Odin system unit.
In order to meet data volume constraints during the aeronomy programme, the AOS offers a number of read-out modes with either a reduced number of bytes per channel, or pre-averaged channel values over a selected part of the spectrum. The default mode used for astronomy observations delivers 1728 32-bit data over the full band. An internal frequency comb generator is switched on, once per orbit, for checking the AOS frequency calibration. The thermal environment of spectrometer is monitored via a number of temperature sensors, whose read-outs are stored within the house-keeping data and as part of the AOS science data.
Raw science and house-keeping data are downloaded at Esrange and transferred to a data archive housed by the Parallel Data Centre (PDC) at the Royal Institute of Technology (KTH) in Stockholm. The PDC in turn notifies the Odin data centre at Onsala Space Observatory about the availability of new radiometer data files. These level 0 files are downloaded and merged with house-keeping data and reconstructed attitude information as outlined above. After proper intensity and frequency calibration they are again uploaded to PDC as level 1 data, where they become available to the scientific teams in the four participating countries. Astronomy level 1 data are stored using binary FITS tables. For the aeronomy data the HDF format was chosen instead.
All software development was carried out on a Linux based system using tools available as open source. A relational database is used for keeping track of data files and processing status. Algorithms for the data retrieval and calibration of the radiometer were developed in the form of a compiled subroutine library. Combined with modern, powerful scripting languages it is possible to quickly build batch procedures and test algorithms; but as well to construct larger programs including graphical user interfaces, database handling and scientific plotting routines.
Acknowledgements
Generous financial support from the Research Councils and Space Agencies in Canada, Finland, France and Sweden is gratefully acknowledged. M. Olberg also acknowledges the work of the many developers of free software, which has contributed much to this project.