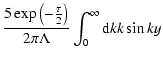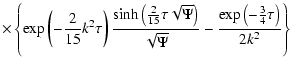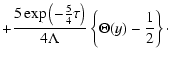A&A 402, 805-817 (2003)
DOI: 10.1051/0004-6361:20030169
Description of non-diffusive solar cosmic ray propagation
in a homogeneous regular magnetic field
Yu. I. Fedorov - B. A. Shakhov
Main Astronomical Observatory National Academy
of Sciences of Ukraine and
Isaac Newton Institute of Chile, Kiev Branch,
03680, Zabolotnoho 27, Kiev, Ukraine
Received 1 August 2002 / Accepted 29 November 2002
Abstract
In the present paper the propagation of energetic charged
particles in a magnetic field with a homogeneous regular component is studied.
On the basis of the Boltzmann equation the analytical expressions for particle
density and anisotropy are derived under instantaneous isotropic injection
of particles into the scattering medium. Starting from the set of
equations for spherical harmonics of the
distribution function the new transport
equation taking into account the second harmonic is carried out. The
solution of this transport equation is reached and comparison with
analytical solutions of the kinetic equation is performed. The telegraph
equations for particle density and flux are derived and their solutions
are analyzed. The transport of energetic particles under multiple small
angle scattering is considered.
Key words: diffusion - radiative transfer - ISM: cosmic rays
The most rigorous treatment of cosmic ray (CR) propagation
in the interplanetary medium and in the Galaxy is based on the kinetic equation
(Earl 1976;
Dorman & Katz 1977; Achatz et al. 1991; Fedorov et al.
1992; Webb et al. 2000). The kinetic equation describes the
transport of energetic particles in the magnetic field, which can be presented
as a superposition
of a mean regular field and magnetic irregularities of various scales.
The regular interplanetary magnetic field has
a spiral configuration and decreases with
heliocentric distance. This spatial variation
of a regular magnetic field causes CR
focusing (Earl 1976; Bazilevskaja & Golynskaja 1989),
and magnetic fluctuations produce the scattering of charged energetic particles
(Dorman & Katz 1977; Toptygin 1985; Achatz et al.
1991; Schlickeiser et al. 1991).
In the present paper we assume a mean magnetic field to be
homogeneous and sufficiently strong, thus the drift approximation is
applicable to the particle motion description. We do not take into
consideration the process of particle cross field diffusion (Dorman et al.
1990; Chuvilgin & Ptuskin 1993; Kirk et al.
1996; Michalek & Ostrowski 1997) and
convection effects in CR, which are due to the interaction of energetic
particles with moving solar wind plasma (Earl 1984; Toptygin
1985; Achatz et al.
1991; Fedorov et al. 1992).
CR scattering on magnetic field irregularities can be treated as
particle interaction with "magnetic clouds'' and can be described by
the Boltzmann collision integral (Gleeson & Axford
1967; Dolginov & Toptygin
1967; Fisk & Axford 1969;
Toptygin 1985). The Boltzmann kinetic equation can be
solved analytically and the exact expression for a Green function can be
obtained, which describes CR distribution after an impulsive injection of
particles with a given velocity direction (Fedorov & Shakhov 1993, 1994).
Kota (1994) has derived an exact formula for particle
density under isotropic,
instantaneous particle release and has also considered CR transport in the case
of anisotropic scattering. Recently, the multiple scattering approach for
the kinetic equation solution was developed (Webb et al. 2000),
which can be succesfully applied to a number of problems
in physical kinetics.
The diffusion approximation, widely used in the theory of CR
transport, proved to be deficient in a number of problems
(Earl 1973;
Toptygin 1985). The telegraph equation description
was applied to the process of
solar CR propagation by many authors (Shishov 1966;
Fisk & Axford 1969; Earl 1973;
Gombosi et al. 1993). Recently, the approximate
methods of the kinetic equation solution, based on the
investigation of a set of equations
for harmonics of the CR distribution function, were developed
(Earl 1994; Zank et al. 1999).
The accuracy of these methods was explored by
comparison with exact analytical solutions of the Boltzmann equation and with
numerical results of Monte Carlo simulations (Earl 1994; Zank et al.
1999).
In the present paper we consider the propagation of energetic particles
under their instantaneous, isotropic injection into scattering medium with a
homogeneous regular magnetic field. Starting from the Boltzmann equation, the
exact analytical expressions for particle density and anisotropy are derived
and approximate formulas valid for late times with respect to the scattering
timescale are obtained (Sect. 2). In Sect. 3 the set of equations for
harmonics of CR distribution function is derived and telegraph equations
for particle density and flux are obtained and solved. The derivation of a
new transport equation taking into account the second harmonic of the
distribution function is carried out and the solution of this equation is
given in Sect. 4. The approximate expressions valid for late times are
considered and results of calculations are compared to the exact analytical
solutions of the Boltzmann equation.
The CR transport governed by the Fokker-Planck
equation is studied in Sect. 5. The derivation of a new transport
equation describing multiple small angle scattering is carried out. In
Sect. 6 the modified telegraph equations, corresponding to Boltzmann and
Fokker-Planck equations, are obtained and solutions of these equations are
analyzed.
In Sect. 7 the transport equation, taking into
consideration anisotropic particle scattering on magnetic irregularities and
solar cosmic ray (SCR)
focusing in the interplanetary magnetic field, is derived. The solutions
of the obtained equations are applied to the analysis of the solar proton
event of July 14, 2000.
Let us start from the kinetic equation describing charged particle
propagation in the interplanetary magnetic field (Toptygin 1985;
Fedorov & Shakhov 1994; Kota 1994)
 |
(1) |
where
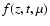 is CR distribution function,
is CR distribution function,
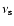 is a collision
frequency, describing interaction of particles with magnetic irregularities
("magnetic clouds''), and
is a collision
frequency, describing interaction of particles with magnetic irregularities
("magnetic clouds''), and  is a particle pitch angle cosine. The
instantaneous isotropic source of particles is included in the right hand side
of Eq. (1). It is supposed that the CR distribution function depends
only on coordinate z along a uniform regular magnetic field.
is a particle pitch angle cosine. The
instantaneous isotropic source of particles is included in the right hand side
of Eq. (1). It is supposed that the CR distribution function depends
only on coordinate z along a uniform regular magnetic field.
After introduction of dimensionless variables
(where
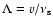 is the particle mean free path) the kinetic
Eq. (1) can be rewritten in the form
is the particle mean free path) the kinetic
Eq. (1) can be rewritten in the form
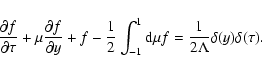 |
(2) |
It is known that the exact solution of kinetic Eq. (2) can be separated
into those particles which have not experienced scattering, and scattered
ones (Fedorov & Shakhov 1993; Kota 1994;
Fedorov et al. 1995; Webb et al. 2000).
The unscattered distribution function, associated with kinetic
Eq. (2), has the form
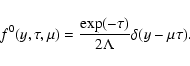 |
(3) |
According to this equation the unscattered particles with pitch angle  in time
in time  are located in a position
are located in a position
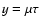 .
.
The solution of kinetic Eq. (2) can be reached by using a Laplace
transform in dimensionless time  and a Fourier transform in
dimensionless spatial coordinate y (Fedorov & Shakhov 1993;
Fedorov et al. 1995).
The CR distribution function can be presented
as an expansion into Legendre polynomials
and a Fourier transform in
dimensionless spatial coordinate y (Fedorov & Shakhov 1993;
Fedorov et al. 1995).
The CR distribution function can be presented
as an expansion into Legendre polynomials
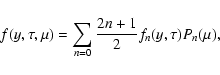 |
(4) |
where quantities
 |
(5) |
represent harmonics of the particle distribution
function. In the present paper
we shall deal only with particle density f0 and particle flux f
1 as functions of time and position.
The density of unscattered particles can be obtained by integration
of distribution function (3) over 
 |
(6) |
where
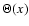 is the Heaviside step function. According to (6) the
unscattered particles are extended in the region
is the Heaviside step function. According to (6) the
unscattered particles are extended in the region
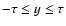 and the number of these particles decays exponentially with time after
injection. Multiplying formula (3) by
and the number of these particles decays exponentially with time after
injection. Multiplying formula (3) by  and integrating over
and integrating over  we
obtain the following expression for the first
harmonic of the unscattered distribution function
we
obtain the following expression for the first
harmonic of the unscattered distribution function
 |
(7) |
The scattered particle density can be written as (Kota 1994)
where
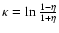 ;
;
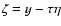 .
Note
that the derivation of this formula is presented in Appendix A.
.
Note
that the derivation of this formula is presented in Appendix A.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f1.eps}
\end{figure}](/articles/aa/full/2003/18/aa1765/Timg27.gif) |
Figure 1:
The dependence of density on the spatial coordinate y(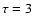 ), curve 1 - kinetic equation solution,
curve 2 - diffusion approximation, curve 3 - telegraph equation solution,
curve 4 - solution of transport Eq. (27),
dashed curve - unscattered particles,
dotted curve - scattered particles. ), curve 1 - kinetic equation solution,
curve 2 - diffusion approximation, curve 3 - telegraph equation solution,
curve 4 - solution of transport Eq. (27),
dashed curve - unscattered particles,
dotted curve - scattered particles. |
The spatial distribution of particles for 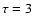 is shown in
Fig. 1, where the dashed curve corresponds to unscattered particles (6),
the dotted curve accounts for scattered particles (8), and the curve 1
gives the density of all particles. One can see that the density of
unscattered particles is uniform in the region
is shown in
Fig. 1, where the dashed curve corresponds to unscattered particles (6),
the dotted curve accounts for scattered particles (8), and the curve 1
gives the density of all particles. One can see that the density of
unscattered particles is uniform in the region 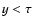 and
the scattered particle density decreases with y. It is worth noting that
the density equals zero for
and
the scattered particle density decreases with y. It is worth noting that
the density equals zero for 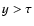 in accordance with the
finite value of particle velocity.
in accordance with the
finite value of particle velocity.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f2.eps}
\end{figure}](/articles/aa/full/2003/18/aa1765/Timg30.gif) |
Figure 2:
The temporal dependence of density in y=2 position,
curve 1 - kinetic equation solution,
curve 2 - diffusion approximation, curve 3 - telegraph equation solution,
curve 4 - solution of transport Eq. (27),
dashed curve - unscattered particles,
dotted curve - scattered particles. |
The temporal profile of particle density at position y=2 is
demonstrated in Fig. 2. One can see that the number of unscattered particles
(presented by dashed curve ) at 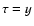 increases drastically from zero
to a finite value, and at
increases drastically from zero
to a finite value, and at 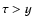 the unscattered particle
density decays exponentially. The density of scattered particles at
the unscattered particle
density decays exponentially. The density of scattered particles at 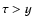 increases continuously from zero at
increases continuously from zero at 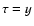 ,
and after a
couple of scattering times the scattered particles dominate the distribution
of all particles, presented in Fig. 2 by curve 1.
,
and after a
couple of scattering times the scattered particles dominate the distribution
of all particles, presented in Fig. 2 by curve 1.
Let us consider the particle distribution at late times, when the
time after injection is much longer than the mean time between collisions (
 ). In this case one can neglect the unscattered particle density (6) and the second term in expression (8), which is small because of the
exponential multiplier. Thus under condition
). In this case one can neglect the unscattered particle density (6) and the second term in expression (8), which is small because of the
exponential multiplier. Thus under condition
 we can obtain from
Eq. (8) the following approximate formula (the derivation of this
expression is done in Appendix A)
we can obtain from
Eq. (8) the following approximate formula (the derivation of this
expression is done in Appendix A)
 |
(9) |
Note that the well known solution of the diffusion equation can be
obtained from (9) by retaining only the first term in brackets. The
diffusion density is shown in Figs. 1, 2 by curve 2; one can see from these
figures that the kinetic equation solution (curve 1) approaches the diffusion
density with increasing time after particle injection.
The derivation of an expression for the first harmonic of the
distribution function from kinetic Eq. (2) can be done in a similar
manner and is presented in Appendix A. The first harmonic of the scattered
distribution function has the form
The anisotropy of CR distribution is defined by the formula
 |
(11) |
and can be calculated starting from equations for f1 (7), (10) and from
Eqs. (6), (8) for
particle density. At late times after particle release the
expression (10) can be simplified and the approximate formula for the first
harmonic can be obtained (Appendix A). Starting with expressions (A.13) and
(9) we can write the formula for anisotropy valid under condition

 |
(12) |
The anisotropy value in the diffusion approximation can be obtained
from Eq. (12) by neglecting the two last terms in the brackets. Figure 3
illustrates the time evolution of particle anisotropy (11) for y=2; in this
figure curve 1 corresponds to the anisotropy value calculated according
expressions (6)-(8), (10), derived from kinetic equation, and curve 2 shows 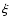 in the diffusion approximation. It is instructive to note that the
first arriving particles (
in the diffusion approximation. It is instructive to note that the
first arriving particles (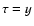 )
offer the maximal anisotropy value
)
offer the maximal anisotropy value 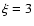 .
One can see from Figs. 1-3 that the diffusion approximation is applicable
only for late times after injection, and the anisotropy calculated on the
basis of the kinetic equation at all times exceeds the corresponding diffusion
value.
.
One can see from Figs. 1-3 that the diffusion approximation is applicable
only for late times after injection, and the anisotropy calculated on the
basis of the kinetic equation at all times exceeds the corresponding diffusion
value.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f3.eps}
\par\end{figure}](/articles/aa/full/2003/18/aa1765/Timg44.gif) |
Figure 3:
The temporal dependence of anisotropy 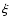 in y=2 position,
curve 1 - kinetic equation solution,
curve 2 - diffusion approximation, curve 3 - telegraph equation solution,
curve 4 - solution of new transport equation.
in y=2 position,
curve 1 - kinetic equation solution,
curve 2 - diffusion approximation, curve 3 - telegraph equation solution,
curve 4 - solution of new transport equation. |
The set of equations for harmonics of CR distribution function can be
obtained by multiplying the kinetic equation by
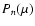 and by integrating the
result from
and by integrating the
result from 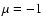 to
to 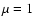 (Earl 1994; Zank et al. 1999).
If we multiply Eq. (2) by 1,
(Earl 1994; Zank et al. 1999).
If we multiply Eq. (2) by 1,  and
and
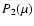 respectively and
integrate over
respectively and
integrate over  we obtain the following set of equations
we obtain the following set of equations
 |
(13) |
 |
(14) |
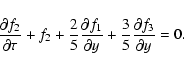 |
(15) |
We can obtain the diffusion approximation if we neglect the first
term in (14) assuming that the time evolution of particle distribution
occurs sufficiently slowly so that
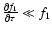 ,
, although neglecting the
second harmonic in comparison to f0 .
In this case the particle flux is proportional to the density gradient
although neglecting the
second harmonic in comparison to f0 .
In this case the particle flux is proportional to the density gradient
 |
(16) |
and Eq. (13) takes the form
 |
(17) |
The solution of the diffusion equation is well known
 |
(18) |
and is presented by curve 2 in Figs. 1, 2. The particle anisotropy 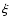 (11)
in the diffusion approximation is given by formula
(11)
in the diffusion approximation is given by formula
 |
(19) |
Curve 2 in Fig. 3 illustrates the evolution of the diffusion anisotropy (19),
which decays inversely proportional to time.
If we neglect the second harmonic in Eq. (14) but
retain the time derivative of f1 we obtain the well-known telegraph
equation (Shishov 1966; Fisk & Axford 1969; Earl 1973;
Dorman et al. 1983; Gombosi et al. 1993)
 |
(20) |
The solution of telegraph Eq. (20) is presented in Appendix B and has
the following form
 |
|
|
(21) |
where
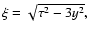 and In(x) stands for the modified
Bessel function of the nth order.
and In(x) stands for the modified
Bessel function of the nth order.
The solution of the telegraph Eq. (21) is illustrated in Figs. 1, 2 by
curve 3. It is worth mentioning that in these figures we do not present the
singular part of the solution (21), which is proportional to 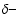 function. One can see from formula (21) and from Fig. 1 (curve 3) that in
this approximation at time
function. One can see from formula (21) and from Fig. 1 (curve 3) that in
this approximation at time  the particles are located only in
region
the particles are located only in
region
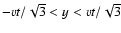 and this region expands with
time with characteristic velocity
and this region expands with
time with characteristic velocity
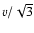 .
It is instructive to note
that the telegraph equation approximation corresponds to the speed of
disturbances propagation
.
It is instructive to note
that the telegraph equation approximation corresponds to the speed of
disturbances propagation
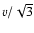 (Shishov 1966;
Fisk et al. 1969;
Gombosi et al. 1993). This value of signal speed as well as the pulses,
propagating on the forward fronts of particle distribution, result from
higher harmonics neglected in the derivation of the telegraph Eq. (20). One
can see from Fig. 2, where the particle density (21) is displayed as a
function of time
(Shishov 1966;
Fisk et al. 1969;
Gombosi et al. 1993). This value of signal speed as well as the pulses,
propagating on the forward fronts of particle distribution, result from
higher harmonics neglected in the derivation of the telegraph Eq. (20). One
can see from Fig. 2, where the particle density (21) is displayed as a
function of time  ,
that the particles appear in y-position
impulsively at
,
that the particles appear in y-position
impulsively at
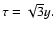 It is instructive to note that the
description based on the commonly used telegraph Eq. (20) does not
improve the accuracy of density and anisotropy calculations in comparison
with the diffusion approximation, in contrast to the modified telegraph equation
derived by Gombosi et al. (1993).
It is instructive to note that the
description based on the commonly used telegraph Eq. (20) does not
improve the accuracy of density and anisotropy calculations in comparison
with the diffusion approximation, in contrast to the modified telegraph equation
derived by Gombosi et al. (1993).
At late times, after particles have undergone many scatters, one can
obtain from (21) the following approximate formula (see Appendix B)
 |
(22) |
Note that expression (22) differs from formula (9), based on the kinetic
equation.
Neglecting the second harmonic of distribution function in the set of
Eqs. (13), (14) one can obtain the telegraph equation for particle flux
 |
(23) |
The solution of this equation, which can be derived
quite similarly to the solution of the telegraph Eq. (20), has the form
 |
|
|
(24) |
The anisotropy of particle distribution 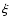 (11),
calculated from (21), (24), is shown in Fig. 3 (curve 3). Note that this
value of anisotropy is fairly close to the value of
(11),
calculated from (21), (24), is shown in Fig. 3 (curve 3). Note that this
value of anisotropy is fairly close to the value of 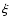 in the diffusion
approximation (19) if
in the diffusion
approximation (19) if
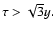 At late times (
At late times (
 )
one
can derive from (22), (24) the following formula
)
one
can derive from (22), (24) the following formula
 |
(25) |
which is different from expression (12), obtained from the kinetic
equation.
In order to derive the CR transport equation, including the second
harmonic of distribution function, we neglect the first and the last terms
in Eq. (15). Thus we suppose that the distribution function evolves
quite slowly with time, so
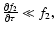 and that the third harmonic is small in comparison with the first one. In
this approximation the second harmonic is proportional to the gradient of f1:
and that the third harmonic is small in comparison with the first one. In
this approximation the second harmonic is proportional to the gradient of f1:
 |
(26) |
Substituting (26) in (14) with using Eq. (13) yields the
following transport equation
 |
|
|
(27) |
The solution of (27) can be obtained by performing Laplace and Fourier
transform methods (Appendix C), and this solution can be written in the form
 |
|
|
(28) |
with
 |
(29) |
The relationship (28) is illustrated in Figs. 1, 2 by curve 4. One can see
from Fig. 2 that obtained expression (28) approximates the kinetic equation
solution (7), (8) (curve 1) fairly well under condition 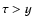 ,
but the
density (28) differs from zero in the region
,
but the
density (28) differs from zero in the region 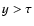 .
The
nonzero value of f0 in this region is caused by using approximate
formula (26) instead of Eq. (15).
.
The
nonzero value of f0 in this region is caused by using approximate
formula (26) instead of Eq. (15).
Let us consider particle distribution (28) long after injection.
Under condition
 the integrand in (28) has a sharp maximum at
k=0, so it can be expanded into series near k=0 (see Appendix A). Then
integrating the obtained expression (A.11) over k we obtain formula (9). It is
interesting to note that at late times the same relationship (9) follows
both from the solution of new transport Eq. (28) and from the kinetic
equation solution (8). Thus a new transport Eq. (27) describes particle
propagation with good accuracy if the time after injection exceeds both a
mean scattering time and the time of unscattered particle propagation from
the source (
the integrand in (28) has a sharp maximum at
k=0, so it can be expanded into series near k=0 (see Appendix A). Then
integrating the obtained expression (A.11) over k we obtain formula (9). It is
interesting to note that at late times the same relationship (9) follows
both from the solution of new transport Eq. (28) and from the kinetic
equation solution (8). Thus a new transport Eq. (27) describes particle
propagation with good accuracy if the time after injection exceeds both a
mean scattering time and the time of unscattered particle propagation from
the source (
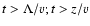 ).
).
Starting from the set of Eqs. (13), (14), (26) one can obtain the
following equation for particle flux
 |
|
|
(30) |
Note that the only difference between equation for f0 (27)
and transport Eq. (30) consists of a source term. So, we can obtain the
solution of (30) in the same manner as expression (28) (see Appendix C), and
this solution has the form
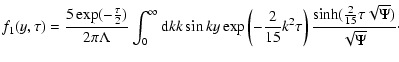 |
|
|
(31) |
The curve 4 in Fig. 3 shows particle anisotropy (11),
calculated on the basis of (28), (31), as a function of time in the case y=2.
The anisotropy of the first arriving particles in this approximation appears
to be smaller than the corresponding value  obtained from the kinetic
equation (curve 1). One can see from Fig. 3 that the accuracy of the
anisotropy calculation given by relationships (28), (31) (curve 4) is higher
than the accuracy of
obtained from the kinetic
equation (curve 1). One can see from Fig. 3 that the accuracy of the
anisotropy calculation given by relationships (28), (31) (curve 4) is higher
than the accuracy of 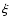 in the diffusion approximation or in the
telegraph equation description (curve 2 and curve 3, correspondingly). At
late times after particle release expression (31) simplifies to (A.12), from
which one can obtain formula (12), derived from the kinetic equation solution.
in the diffusion approximation or in the
telegraph equation description (curve 2 and curve 3, correspondingly). At
late times after particle release expression (31) simplifies to (A.12), from
which one can obtain formula (12), derived from the kinetic equation solution.
Now we consider the kinetic equation, describing multiple
scattering of particles on magnetic irregularities (Earl 1976; Toptygin
1985; Achatz et al. 1991)
 |
(32) |
where
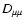 represents the diffusion coefficient in
angular space. Under isotropic scattering, the diffusion coefficient is given
by (Earl 1976; Schlickeiser et al. 1991)
represents the diffusion coefficient in
angular space. Under isotropic scattering, the diffusion coefficient is given
by (Earl 1976; Schlickeiser et al. 1991)
 |
(33) |
where 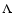 is the particle mean free path.
is the particle mean free path.
Using the dimensionless variables the Fokker-Planck Eq. (32) can be
rewritten as
 |
(34) |
The set of equations for harmonics of distribution
function can be obtained by multiplying Eq. (34) by
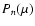 and
by integrating the result over
and
by integrating the result over  .
The first two equations are given by
formulas (13), (14), and the third equation of the set has the form
.
The first two equations are given by
formulas (13), (14), and the third equation of the set has the form
 |
(35) |
This equation differs from (15) only by the coefficient at the
second harmonic. Equations (13) and (14) can be obtained both from
Boltzmann equation and from Fokker-Planck equation. Thus, if we neglect the
second harmonic in (14) we can obtain the same diffusion Eq. (17) or
telegraph Eq. (20) from kinetic Eqs. (2) and (34).
In order to derive the transport equation, including the second
spherical harmonic, we suppose that the second harmonic varies sufficiently
slowly with time and we neglect the third harmonic in (35). The Eq. (35)
can then be written as
 |
(36) |
So in this approximation the second harmonic is proportional to
the gradient of f1. It is worth mentioning that a multiplier in the
right hand side of (36) is 3 times less than in the analogous expression (26).
From the set of Eqs. (13), (14), (36) one can obtain the following
transport equation
 |
|
|
(37) |
This equation differs from the analogous Eq. (27) only by the
coefficient at the mixed derivative.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f4.eps}
\end{figure}](/articles/aa/full/2003/18/aa1765/Timg87.gif) |
Figure 4:
The temporal dependence of particle density in y=1 position,
curve 1 - solution of transport Eq. (27),
curve 2 - solution of transport Eq. (37),
dashed curve - diffusion approximation. |
Thus, the solution of (37) can be
obtained quite similar to the solution of (27) (which is derived in
Appendix C), and can be written as
 |
|
|
(38) |
with
 |
(39) |
As in relationship (28), the integration interval in (38) should be
divided into three parts. If k<k1 or k>k2the integrand is defined as in formula (38), but in the case
k1<k<k2it is necessary to replace in (38) the functions 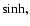
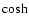 by
by 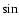 ,
,
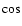 ,
and to change the sign of
,
and to change the sign of 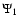 (39) (see Appendix
C). The quantities k1, k2 are defined by relations:
(39) (see Appendix
C). The quantities k1, k2 are defined by relations:
 |
(40) |
The expression (38) can be rewritten in the form
Note that from Eq. (41) the occurrence of a singularity in
y=0 is evident.
One can show that at late times the expression for particle density
(41) simplifies to
 |
(42) |
Formula (42) is different from expression (9), resulting from
kinetic Eq. (2), which corresponds to CR scattering on "magnetic
clouds'' (hard sphere scattering). In Fig. 4 particle density versus
dimensionless time in y=1 position is shown. The dashed curve corresponds
to the diffusion approximation (18), the curve 1 illustrates solution (28) of
the transport Eq. (27), and the curve 2 presents formula (38), describing
the solution of Eq. (37). It is interesting to note that multiple small
angle scattering is characterized by sharper maximum and earlier phase of
maximal intensity in comparison with the case of hard sphere scattering
(Fig. 4).
Starting from the set of Eqs. (13), (14), (36) one can obtain the
following equation for the first harmonic of the distribution function
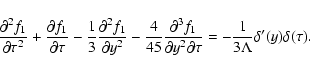 |
(43) |
Equation (43) differs from the analogous Eq. (30), derived from
kinetic Eq. (2), only by the coefficient at the mixed derivative, and
the solution of (43) can be written in the form
 |
|
|
(44) |
We can rewrite expression (44) as following
It is obvious from this formula that the impulsive variation of f1 occurs at y=0 (see also relationship (C.7)).
The calculations show that the anisotropy (11), obtained by
using formulas (38), (44), is somewhat higher than the corresponding value
calculated in accordance with expressions (28), (31). Thus under the same
value of particle mean free path the higher anisotropy value and more
pronounced maximum of temporal intensity profile is typical in the case of
small angle scattering in comparison with hard sphere scattering (Fig. 4). It
is instructive to note that in this approximation the anisotropy of first
arriving particles  takes the value somewhat below the maximal
level of
takes the value somewhat below the maximal
level of  ,
obtained from the kinetic equation.
,
obtained from the kinetic equation.
At late times after particle injection from Eqs. (42), (44)
we obtain the approximate formula
 |
(46) |
which is different from expression (12) obtained from kinetic
Eq. (2).
The new transport equations derived in this paper are associated with
modified telegraph equations obtained by Gombosi et al. (1993). It is
interesting to emphasize that the same diffusion Eq. (17) and telegraph
Eq. (20) follow from the Boltzmann Eq. (2) as well as from the
Fokker-Planck Eq. (34) if the corresponding mean free path values
coincide. However, the transport Eqs. (27) and (37) associated with
kinetic Eqs. (2) and (34) are different from one another. It was
demonstrated by Gombosi et al. (1993)
that more rigorous derivation leads to
the form of the telegraph equation that is different from (20).Thus in the case
of large angle scattering the signal speed in modified telegraph equation
equals
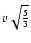 in contrast to the
in contrast to the
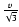 value of
disturbances propagation speed in Eq. (20). Under small angle
scattering one can obtain the modified telegraph equation with the
characteristic propagation speed of
value of
disturbances propagation speed in Eq. (20). Under small angle
scattering one can obtain the modified telegraph equation with the
characteristic propagation speed of
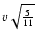 ,
which is below
the particle velocity value (Gombosi et al. 1993).
Let us transform the transport Eq. (27) in the telegraph equation
form. In order to replace a mixed derivative in (27) one can use the
diffusion equation. Differentiating (17) we can obtain the approximate
relation for the mixed derivative which appears to be proportional to the second
order time derivative of particle density. Substituting the obtained
expression into transport Eq. (27) yields
,
which is below
the particle velocity value (Gombosi et al. 1993).
Let us transform the transport Eq. (27) in the telegraph equation
form. In order to replace a mixed derivative in (27) one can use the
diffusion equation. Differentiating (17) we can obtain the approximate
relation for the mixed derivative which appears to be proportional to the second
order time derivative of particle density. Substituting the obtained
expression into transport Eq. (27) yields
 |
|
|
(47) |
Hence starting from transport Eq. (27) we reach the modified
telegraph Eq. (47), derived in the paper of Gombosi et al. (1993).
The solution of the modified telegraph Eq. (47), which can be
obtained quite similarly to the solution of (20)
(Appendix B), is given by
with
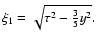 It is
interesting to note that starting from (48) one can obtain expression (9)
corresponding to the exact solution of the kinetic equation
in the case
It is
interesting to note that starting from (48) one can obtain expression (9)
corresponding to the exact solution of the kinetic equation
in the case
 Eq. (20) has another asymptotic (22).
Eq. (20) has another asymptotic (22).
Quite similarly we can use the diffusion approximation relations and
equation for the first harmonic (30) to derive the following modified
telegraph equation for f1
 |
(49) |
The solution of this equation can be written in the form
It is instructive to note that for large values of  from (48), (50) we can reach an approximate formula for anisotropy (12). Thus
for late times we obtain the same relationship (12) from the exact kinetic
equation solution, from the new transport equation and from the modified telegraph
equation.
from (48), (50) we can reach an approximate formula for anisotropy (12). Thus
for late times we obtain the same relationship (12) from the exact kinetic
equation solution, from the new transport equation and from the modified telegraph
equation.
Let us derive the modified telegraph equation corresponding to the
Fokker-Planck Eq. (34). In this case from the transport Eq. (37) one
can obtain
 |
|
|
(51) |
This equation differs from (47) by the coefficient at the second
order time derivative. As a result, the telegraph Eq. (51) is
characterized by the signal propagation speed
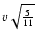 ,
which
issmaller than the particle velocity. The solution of Eq. (51) can be
written as
,
which
issmaller than the particle velocity. The solution of Eq. (51) can be
written as
with
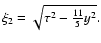 It is instructive to note that in the limit
It is instructive to note that in the limit
 from (52) follows
the approximate formula for particle density (42), which was derived from
solution (38) of transport Eq. (37).
from (52) follows
the approximate formula for particle density (42), which was derived from
solution (38) of transport Eq. (37).
From Eq. (43) one can obtain the following equation for f1
 |
|
|
(53) |
which differs from the analogous Eq. (49) only by the
coefficient at the second order time derivative and as a consequence
incorporates another value of the signal speed. The solution of Eq. (53) has
the form
Note that under condition
 from (52), (54) there follows an
approximate formula for particle anisotropy (46), derived from expressions (41), (44).
from (52), (54) there follows an
approximate formula for particle anisotropy (46), derived from expressions (41), (44).
It is well known that energetic particle scattering in the
interplanetary medium is anisotropic (Denskat et al. 1982;
Toptygin 1985; Dröge et al. 1993).
In the present section we shall
derive the CR transport equation taking into account the anisotropic
scattering of particles by magnetic irregularities and CR focusing in the
diverging interplanetary magnetic field. Energetic particle scattering in
the interplanetary medium is caused by magnetic fluctuations, whose
frequency spectrum has approximately a power law shape with the spectral index
q varying from 1.5 to 1.9 (Denskat et al. 1982;
Toptygin 1985; Dröge et al. 1993).
The intensity of scattering is characterized by the particle mean
free path  , which is associated with a diffusion
coefficient in angular space
, which is associated with a diffusion
coefficient in angular space
 by a known relation
(Hasselmann & Wibberenz 1968;
Beeck & Wibberenz 1986; Dröge 2000)
by a known relation
(Hasselmann & Wibberenz 1968;
Beeck & Wibberenz 1986; Dröge 2000)
 |
(55) |
The diffusion coefficient
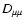 can be
calculated starting from the known spectrum of magnetic field irregularities
(Jokipii 1966; Hasselmann & Wibberenz 1968;
Schlickeiser 1989).
For a power spectrum with a spectral
index
can be
calculated starting from the known spectrum of magnetic field irregularities
(Jokipii 1966; Hasselmann & Wibberenz 1968;
Schlickeiser 1989).
For a power spectrum with a spectral
index 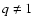 the scattering is anisotropic, and the diffusion
coefficient can be written in a form
(Jokipii 1966; Schlickeiser 1989)
the scattering is anisotropic, and the diffusion
coefficient can be written in a form
(Jokipii 1966; Schlickeiser 1989)
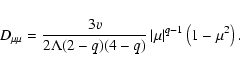 |
(56) |
Note that under condition q =1 isotropic scattering occurs and
in this case the quantity
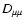 is described by the
formula (33).
is described by the
formula (33).
Energetic particles propagating in the interplanetary medium
are focused by the magnetic field owing to decreasing of the field magnitude
with heliocentric distance
(Earl 1976; Toptygin 1985;
Beeck & Wibberenz 1986).
We shall consider this effect in the approximation of the radial
regular magnetic field. In this case the focusing length is equal to
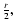 where r is a heliographic coordinate, and the kinetic
equation, describing CR propagation, takes the form
where r is a heliographic coordinate, and the kinetic
equation, describing CR propagation, takes the form
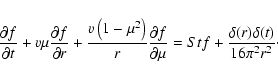 |
(57) |
The instantaneous source of particles is included in the
right hand side of Eq. (57), and a collision integral Stfrepresents CR scattering by magnetic irregularities. By neglecting a
transfer of magnetic irregularities by the solar wind plasma and an inverse
action of CR on the interplanetary magnetic field, the collision integral can
be written as
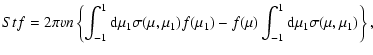 |
|
|
(58) |
where n is the scattering center density, and
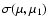 stands for the scattering cross-section.
stands for the scattering cross-section.
In the following we shall assume the scattering to be
anisotropic and represent the scattering section as an expansion restricted
to the second order Legendre polynomial (Case & Zweifel 1967)
 |
(59) |
Note that the isotropic scattering is associated with 
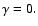 The scattering is linearly anisotropic if
The scattering is linearly anisotropic if 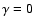 ,
and parameter
,
and parameter 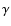 characterizes the
contribution of quadratic anisotropic scattering
(Case & Zweifel 1967).
It is instructive to emphasize that the magnitudes of
characterizes the
contribution of quadratic anisotropic scattering
(Case & Zweifel 1967).
It is instructive to emphasize that the magnitudes of 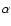 and
and 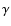 cannot be arbitrary, as the scattering section (59)
should acquire only positive values.
cannot be arbitrary, as the scattering section (59)
should acquire only positive values.
Let us define a collision frequency as
 |
(60) |
and introduce the dimensionless variables
 |
(61) |
where
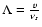 is the
particle mean free path. Then the kinetic Eqs. (57), (58) can be
rewritten in the form
is the
particle mean free path. Then the kinetic Eqs. (57), (58) can be
rewritten in the form
 |
|
|
(62) |
where the relationship
 |
(63) |
defines the harmonics of the CR distribution function.
Multiplying Eq. (62) accordingly by 1,  and
and
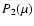 and integrating over
and integrating over  from -1 to 1, one can obtain a set of equations for distribution function harmonics
from -1 to 1, one can obtain a set of equations for distribution function harmonics
 |
(64) |
 |
(65) |
 |
(66) |
Neglecting quantities f2 and
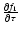 in (65) one can derive from (64), (65) the
diffusion equation. It should be noted that the derived equation is
associated with a diffusion coefficient which differs from the corresponding
value under isotropic scattering by the
in (65) one can derive from (64), (65) the
diffusion equation. It should be noted that the derived equation is
associated with a diffusion coefficient which differs from the corresponding
value under isotropic scattering by the
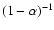 multiplier.
multiplier.
We neglect in (66) the third harmonic and the time
derivative, and we can obtain the approximate relationship for the second
harmonic of the CR distribution function
 |
(67) |
Using (67), from Eqs. (64), (65), we get the following transport
equation
The solution of Eq. (68) can be reached by integral
transformations (Appendix C) and has the following form
with
![$\displaystyle \Gamma (k)=k^{4}-\frac{15}{4}(1-\gamma )(3+2\alpha -5\gamma )k^{2}+\left[
\frac{15}{4}(1-\alpha )(1-\gamma )\right] ^{2}.$](/articles/aa/full/2003/18/aa1765/img166.gif) |
|
|
(70) |
It can be shown (Appendix A) that long after injection (i.e. at
large values of dimensionless time  )
the expression (69)
simplifies essentially
)
the expression (69)
simplifies essentially
![$\displaystyle f_{0}(y,\tau )=\frac{\left[ 3(1-\alpha )\right] ^{\frac{3}{2}}\ex...
... )\tau }
+3\frac{(\alpha -\gamma )\rho ^{2}}{(1-\gamma )\tau ^{2}}\right\}\cdot$](/articles/aa/full/2003/18/aa1765/img167.gif) |
|
|
(71) |
It should be noted that the solution of the diffusion equation
follows from (71) by neglecting two last terms in brackets. It is obvious from
(71) that the linearly anisotropic scattering results in a mean free path
modification, thus the multiplier
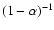 appears in the
mean free path expression in comparison with the isotropic scattering case.
The calculations demonstrate that solution (69) of the transport Eq. (68) corresponds to the later onset of CR intensity enhancement and to
the sharper maximum of a temporal intensity profile compared to the
solution of the diffusion equation.
The value of the maximum intensity enhancement
and the sharpness of time intensity profile rises with increasing of
appears in the
mean free path expression in comparison with the isotropic scattering case.
The calculations demonstrate that solution (69) of the transport Eq. (68) corresponds to the later onset of CR intensity enhancement and to
the sharper maximum of a temporal intensity profile compared to the
solution of the diffusion equation.
The value of the maximum intensity enhancement
and the sharpness of time intensity profile rises with increasing of 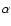 ,
describing the contribution of linearly
anisotropic scattering. The increase of quadratic anisotropic scattering
(represented by
,
describing the contribution of linearly
anisotropic scattering. The increase of quadratic anisotropic scattering
(represented by 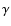 )
leads to a more smoothly varying temporal
intensity profile and to a decrease of maximum value of the SCR enhancement.
)
leads to a more smoothly varying temporal
intensity profile and to a decrease of maximum value of the SCR enhancement.
In order to illustrate the temporal profile of SCR
enhancement, described by the relationship (69), we have made some calculations
concerning the solar proton event of July 14, 2000. This SCR flare was most
powerful in the current cycle of solar activity until April, 2001
(Belov et al. 2001).
The anisotropy data of relativistic protons, obtained on a world-wide
network of neutron monitors, indicate the impulsive nature of this event
(Belov et al. 2001; Pchelkin et al. 2001;
Bieber et al. 2002), that allows us
to use the solution of the transport equation associated with an instantaneous
particle injection. We shall consider 10.20 UT as the moment of energetic
particle release from the Sun of July 14, 2000; this time is associated with
the start of radiowave, X-ray and 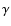 -ray emission (Belov
et al. 2001; Pchelkin et al. 2001;
Bieber et al. 2002). It should be emphasized that
the arrival of the first relativistic protons was registered
on Earth at 10.30 UT which does not contradict a particle injection
near the Sun at 10.20 UT.
-ray emission (Belov
et al. 2001; Pchelkin et al. 2001;
Bieber et al. 2002). It should be emphasized that
the arrival of the first relativistic protons was registered
on Earth at 10.30 UT which does not contradict a particle injection
near the Sun at 10.20 UT.
In Fig. 5 the 1-min data of the neutron monitor Sanae are
shown; this CR station detected one of the most considerable enhancements
the neutron monitors network in a given event (maximum intensity enhancement
according to 1-min data amounts to 53 percent relative to the galactic CR
background). The time in minutes is given in Fig. 5 after the injection
moment at 10.20. It is instructive to note the complex shape of the
experimental curve on the rising phase of CR intensity, starting around the
20th minute and lasting about 20 min. Possible reasons for this
effect could be inhomogeneous local propagation conditions of energetic
particles or fluctuations of the interplanetary magnetic field orientation. The
dotted curve in Fig. 5 corresponds to the diffusion equation solution, the
dashed curve represents the solution (69) of the transport Eq. (68)
under isotropic scattering, and the solid curve introduces the case of
linearly anisotropic scattering (
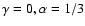 ). In all
cases the mean free path was selected from a condition of coincidence of the
calculated CR maximum with the moment of maximal intensity detected on the
neutron monitor Sanae (33 min after 10.20 UT of July 14, 2000). The mean
free path
). In all
cases the mean free path was selected from a condition of coincidence of the
calculated CR maximum with the moment of maximal intensity detected on the
neutron monitor Sanae (33 min after 10.20 UT of July 14, 2000). The mean
free path
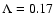 AU corresponds to isotropic scattering,
and
AU corresponds to isotropic scattering,
and
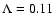 AU is associated with the linearly anisotropic
scattering according to a decrease in
AU is associated with the linearly anisotropic
scattering according to a decrease in 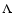 with increase of
scattering anisotropy.
with increase of
scattering anisotropy.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f5.eps}
\end{figure}](/articles/aa/full/2003/18/aa1765/Timg171.gif) |
Figure 5:
The temporal profile of solar particle event of July 14, 2000, as
recorded by the neutron monitor Sanae and calculated enhancements of CR
intensity. Time is in minutes after energetic particle injection near
the Sun (the SCR release was supposed to occur at 10.20 UT). The dotted
curve corresponds to the diffusion approximation, the dashed curve
illustrates the solution (69) under isotropic scattering, and the solid line
is associated with (69) in the case of linearly anisotropic scattering (
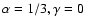 ). ). |
The event of July 14, 2000 is characterized by sufficiently
intensive scattering, so the mean free path is small in comparison to the
distance to the particle source. Because of this the relationship (69) (the
dashed and solid curves in Fig. 5) differ markedly from the solution of the
diffusive equation (dotted curve) only during about the first 15 min after
the first particle arrival. The temporary profiles of SCR intensity,
calculated according to (69) (solid and dashed curves in Fig. 5) are
different from one another for a still shorter period of time. Note that the
calculation in the case of anisotropic scattering (solid curve in Fig. 5)
better approximates the early phase of CR intensity enhancement compared to
the isotropic scattering (dashed curve in Fig. 5).
In the present paper the propagation of charged energetic particles
in homogeneous regular magnetic field under isotropic scattering on magnetic
irregularities is considered. The exact analytical solutions of the Boltzmann
equation for particle density and anisotropy are derived and these solutions
are compared with results obtained with various approximate methods (such as
diffusion approximation, telegraph equation description and the new transport
equation approach). It is shown that
the obtained expressions (9), (12) (valid for late
times) in a zero order approximation with respect to
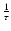 coincide with the diffusion and telegraph equation descriptions. It is worth
noting that in the first order approximation relative to
coincide with the diffusion and telegraph equation descriptions. It is worth
noting that in the first order approximation relative to
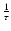 the
results obtained from the kinetic equation
and from the telegraph equation approach
differ from one another.
the
results obtained from the kinetic equation
and from the telegraph equation approach
differ from one another.
The new CR transport equations taking into account the second
harmonic of the distribution function are derived and solutions of these
equations are presented. The calculations show that density and anisotropy
values obtained from the new transport equation fit the exact solutions of
the Boltzmann equation much better than corresponding expressions derived with
diffusion approximation or with the telegraph equation approach. At late times
the solutions of the new transport equations satisfy the relationships (9), (12),
obtained from kinetic equation solutions. It is instructive to note that
solutions of the new transport Eqs. (28), (31) describe particle
distribution with good accuracy but not shortly after injection
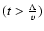 for reasonably short distances from the particle source
(z<vt), it is not close to the boundaries of the region filled by particles.
for reasonably short distances from the particle source
(z<vt), it is not close to the boundaries of the region filled by particles.
The CR propagation also can be studied on the basis of the Fokker-Planck
equation, describing the process of multiple small angle scattering. The
diffusion and telegraph equations, derived from the Fokker-Planck equation, are
the same as from the Boltzmann equation, provided the mean free path values
coincide. However, the new transport Eq. (37), derived from the
Fokker-Planck equation, is different from the corresponding Eq. (27).
Calculations show that in the case of multiple small angle scattering the
temporal profile of particle density exhibit a sharper maximum and anisotropy
takes higher values in comparison with corresponding quantities, obtained on
the basis of the Boltzmann equation.
Starting from kinetic Eqs. (1) and (32), modified telegraph
equations for particle density and anisotropy are obtained and solutions of
these equations are presented. Derived Eqs. (47), (51) correspond to
different speeds of disturbance propagation in accordance with conclusions
of Gombosi et al. (1993).
It is interesting to note that at late times the
results for particle density and anisotropy obtained from new transport
equations and derived from modified telegraph equations coincide in the
first order approximation with respect to the small parameter
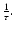
The new transport equation derived in this paper allows us to describe the
spatial-temporal particle distribution with good accuracy if the time after
injection is not small in comparison with the inverse scattering frequency.
It is instructive to note that this description proves to be more correct
than the diffusion and telegraph equation approximations. This approach can
be successfully applied to problems more complicated than the process of CR
propagation in homogeneous regular magnetic fields under isotropic scattering
of particles, considered in this paper.
On the basis of a kinetic equation taking into account
magnetic focusing of energetic charged particles and the anisotropic nature
of CR scattering on magnetic irregularities, a new transport equation is
derived. The regular magnetic field was supposed to be radial, and the particle
scattering cross-section on "magnetic clouds'' was described by
relationship (59) (Case & Zweifel 1967).
The solution of this equation is
applied to the analysis of Sanae neutron monitor data for the solar proton event
of July 14, 2000. It is shown that for this event the case of linearly
anisotropic scattering better approximates the initial phase of SCR
enhancement than the isotropic scattering approach.
In this appendix we shall consider briefly the derivation
of expressions for particle density f0 and for the first harmonic of
the distribution function f1 starting from the kinetic equation. We shall
deduce also the approximate formulas (9), (12) which are valid for late times
after particle injection.
Let us introduce a new function according to the following equation
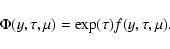 |
(A.1) |
By performing a Fourier transform of the spatial variable y and
a Laplace transform of the temporal variable 
 |
(A2) |
we can derive from kinetic Eq. (2) the following formula for
the Fourier-Laplace transform of the distribution function
 |
(A.3) |
The first term in formula (A.3) corresponds to unscattered
particles, whose distribution function can be obtained by performing the
inverse Laplace and Fourier transformations. In order to derive the
Fourier-Laplace transform of scattered particle density we integrate the
second term in (A.3) over 
 |
(A.4) |
The expression for a Fourier-Laplace transform of the first
harmonic of the scattered distribution function can be obtained by multiplying
the second term in (A.3) by  and by integrating over
and by integrating over  from -1 to 1
from -1 to 1
 |
(A.5) |
Following from our previous papers (Fedorov & Shakhov 1994;
Fedorov et al. 1995) we perform first an inverse Laplace transformation.
The function of the complex variable 
 |
(A.6) |
has two branch points
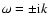 (Sidorov et al. 1982),
therefore to define unique branches of the analytic functions (A.4), (A.5) it is
necessary to make a branch cut in the complex
(Sidorov et al. 1982),
therefore to define unique branches of the analytic functions (A.4), (A.5) it is
necessary to make a branch cut in the complex 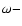 plane along the
imaginary axis from
plane along the
imaginary axis from 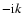 to
to 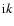 .
The equation
.
The equation
 |
(A.7) |
has a unique root
 |
(A.8) |
if the condition
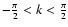 is
satisfied. In the opposite case
is
satisfied. In the opposite case
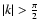 the
Eq. (A.7) has no solution. Therefore, functions (A.4), (A.5) of the complex
variable
the
Eq. (A.7) has no solution. Therefore, functions (A.4), (A.5) of the complex
variable  have two branch points
have two branch points
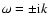 and the pole of
the first order
and the pole of
the first order
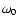 (A.8). The inverse Laplace transform leads to
the following expressions:
(A.8). The inverse Laplace transform leads to
the following expressions:
with
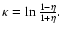 The first term in formulas (A.9), (A.10) is due to the calculation of the pole in
the point
The first term in formulas (A.9), (A.10) is due to the calculation of the pole in
the point
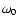 (A.8) and the condition of this singularity existence
is manifested as the difference of the Heaviside step functions. The second
term in (A.9), (A.10) arises as a result of integration along the edges of the
branch line on the imaginary axis. Performing the inverse Fourier
transformation we obtain expressions (8) and (10), describing two first
harmonics of the scattered distribution function.
(A.8) and the condition of this singularity existence
is manifested as the difference of the Heaviside step functions. The second
term in (A.9), (A.10) arises as a result of integration along the edges of the
branch line on the imaginary axis. Performing the inverse Fourier
transformation we obtain expressions (8) and (10), describing two first
harmonics of the scattered distribution function.
Let us now consider the approximate formulas valid long after
injection when particles have undergone many scatters and the distribution
function becomes close to isotropic. In this case we can neglect the second
term in the formula for scattered density (8), which is proportional to the
exponentially small multiplier. If the time after particle release is much
more than the scattering time, the number of unscattered particles (7) is also
negligible. The integrand in the first term in (8) has a sharp maximum in the
neighborhood of k=0. Thus, expanding the integrand in a series near k=0 and
extending the integration to the infinity yields
Then we can integrate (A.11) using known relationships (Prudnikov
et al. 1981) and obtain expression (9)
for the particle density, which is valid
under the condition
 .
.
From relationship (10), describing the first harmonic of scattered
particle distribution, one can obtain the expression valid for late times
After integration (Prudnikov et al. 1981) we derive the following
expression
 |
(A.11) |
Taking into account the minority of quantities
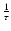 and
and
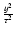 from Eqs. (A.13), (9) one can obtain a formula
for particle anisotropy (12).
from Eqs. (A.13), (9) one can obtain a formula
for particle anisotropy (12).
We present the derivation of solution (21) of the telegraph Eq. (20). If we introduce a new function
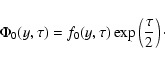 |
(B.1) |
Equation (20) takes the form
 |
|
|
(B.2) |
From (B.2) using (A.2) one can reach the following formula for the
Fourier-Laplace transform of function 
 |
(B.3) |
Performing an inverse Fourier transformation we obtain
 |
(B.4) |
In order to perform an inverse Laplace transformation one can
use the following relationship (Sidorov et al. 1982)
 |
|
|
(B.5) |
Thus one can obtain the expression
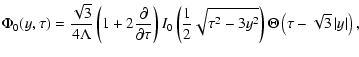 |
|
|
(B.6) |
which is followed by formula (21) for particle density.
It is worth noting that expression (22) valid under condition
 can be obtained from (21) by applying an asymptotic expression of a
modified Bessel function, which is valid for large values of x(Abramowitz & Stegun 1964)
can be obtained from (21) by applying an asymptotic expression of a
modified Bessel function, which is valid for large values of x(Abramowitz & Stegun 1964)
 |
(B.7) |
In this section we present the derivation of solution (28) of the transport Eq. (27). Let us introduce the function  according to (B.1). Performing the Fourier-Laplace transformation of Eq. (27) one can obtain the following formula
according to (B.1). Performing the Fourier-Laplace transformation of Eq. (27) one can obtain the following formula
 |
|
|
(C.1) |
with  defined by (29).
defined by (29).
Let us perform first an inverse Laplace transformation. The function
of the complex variable  (C.1) has two poles, so by calculating
the residual values we can obtain the relationship
(C.1) has two poles, so by calculating
the residual values we can obtain the relationship
 |
|
|
(C.2) |
Performing an inverse Fourier transformation of (C.2) we derive
expression (28) for particle density.
Note that the function  (29) becomes negative
for
k1<k<k2, where
(29) becomes negative
for
k1<k<k2, where
 |
(C.3) |
Thus, the interval of integration in (28) splits into three
parts, with the integrand as in (28) under integration from 0
to k1 and from k2 to the infinity, while if
k1<k<k2 it is
necessary in (28) to replace sinh(x) and cosh(x) by sin(x) and cos(x)
respectively. Consequently, we can rewrite (28) as
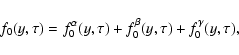 |
(C.4) |
with
and
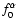 ,
,
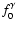 differ from (28) only by
the limits of integration.
differ from (28) only by
the limits of integration.
One can show that for large values of k the integrand in (28) approaches
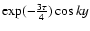 .
Let us rewrite
expression (28) in the form
.
Let us rewrite
expression (28) in the form
Note that from (C.6) the singularity occurrence in y=0 is
evident. The integrand in (C.6) decays with increasing k proportional to
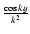 ,
so the integral in (C.6) converges quite well (in
contrast with expression (C.5)). The singularity occurrence in (C.6) is due to the
approximation used in the transport equation derivation, i.e. results
from replacement of (15) by the approximate formula (26).
,
so the integral in (C.6) converges quite well (in
contrast with expression (C.5)). The singularity occurrence in (C.6) is due to the
approximation used in the transport equation derivation, i.e. results
from replacement of (15) by the approximate formula (26).
Quite similarly one can show that the integrand in Eq. (31), describing the first harmonic of the particle distribution,
approaches at large kto
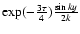 .
Thus, the
relationship (31) can be rewritten as
.
Thus, the
relationship (31) can be rewritten as
From (C.7) the jump of f1 in the y=0 position is evident. Note
that the magnitude of this jump decays exponentially with time. The
occurrence of such a discontinuity in f1 at the origin is typical only
of a given approximation. In fact the quantity f1 (7), (10) derived from
the kinetic equation approaches zero continuously when y tends to 0.
- Abramowitz, M., & Stegun, I. A. 1964,
Handbook of mathematical functions
(New York: Dover), 832
- Achatz, U., Steinacker, J., & Schlickeiser, R. 1991,
A&A, 250, 266
NASA ADS
- Bazilevskaya, G. A., & Golynskaya, R. M. 1989,
Geomagn. Aeronomy, 29, 204
-
Beeck, J., & Wibberenz, G. 1986, ApJ, 311, 437
NASA ADS
-
Belov, A. V., Bieber, J. W., Eroshenko, E. A., et al. 2001,
Proc. 27th Intern. Cosmic Ray Conf. (Hamburg), 3, 3446
-
Bieber, J. W., Dröge, W., Evenson, P. A., et al. 2002, ApJ, 567, 622
NASA ADS
-
Case, K. M., & Zweifel, P. F. 1967, Linear transport theory
(Reading: Addison-Wesley Publ. Comp.)
- Chuvilgin, L. G., & Ptuskin, V. S. 1993,
A&A, 279, 278
NASA ADS
-
Denskat, K. U., & Neubauer, F. M. 1982, JGR, 87, 2215
NASA ADS
- Dolginov, A. Z., & Toptygin, I. N. 1967,
Geomagn. Aeronomy, 7, 967
- Dorman, L. I., & Katz, M. E. 1977,
Space Sci. Rev., 20, 529
NASA ADS
- Dorman, L. I., Katz, M. E.,
& Stehlik, M. 1990,
Bull. Astron. Inst. Czecosl., 41, 312
- Dorman, L. I., Katz, M. E.,
Fedorov, Yu. I., & Shakhov, B. A. 1983,
Proc. 18th Intern. Cosmic Ray Conf. (Bangalore), 10, 63
-
Dröge, W., Achatz, U., Wanner, W., Schlickeiser, R., &
Wibberenz, G. 1993, ApJ, 407, L95
NASA ADS
-
Dröge, W. 2000, ApJ, 537, 1073
NASA ADS
- Earl, J. A. 1973, ApJ, 180, 227
NASA ADS
- Earl, J. A. 1976, ApJ, 205, 900
NASA ADS
- Earl, J. A. 1984, ApJ, 278, 825
NASA ADS
- Earl, J. A. 1994, ApJ, 425, 331
NASA ADS
- Fedorov, Yu. I., Katz, M. E., Kichatinov, L. L.,
& Stehlik, M. 1992, A&A, 260, 499
NASA ADS
- Fedorov, Yu. I., & Shakhov, B. A. 1993,
Proc. 23rd Intern. Cosmic Ray Conf. (Calgary), 3, 215
- Fedorov, Yu. I., & Shakhov, B. A. 1994,
Geomagn. Aeronomy, 34, 19
- Fedorov, Yu. I., Shakhov, B. A.,
& Stehlik, M. 1995, A&A, 302, 623
NASA ADS
- Fisk, L. A., & Axford, W. I. 1969,
Sol. Phys., 7, 486
NASA ADS
- Gleeson, L. J., & Axford, W. I. 1967,
ApJ, 149, L115
NASA ADS
- Gombosi, T. J., Jokipii, J. R.,
Kota, J., Lorencz, K., & Williams, L. L. 1993, ApJ, 403, 377
NASA ADS
-
Hasselmann, K., & Wibberenz, G. 1968, Z. Geophys., 34, 353
-
Jokipii, J. R. 1966, ApJ, 146, 480
NASA ADS
- Kirk, J. G., Duffy, P., & Gallant, Y. A. 1996,
A&A, 314, 1010
NASA ADS
- Kota, J. 1994, ApJ, 427, 1035
NASA ADS
- Michalek, G., & Ostrowski, M. 1997,
A&A, 326, 793
NASA ADS
-
Pchelkin, V. V., Vashenyuk, E. V., & Gvozdevsky, B. B. 2001,
Proc. 27th Intern. Cosmic Ray Conf. (Hamburg), 3, 3379
- Prudnikov, A. P., Brychkov, Yu. A.,
& Marichev, O. I. 1981, Integrals and series (Moscow: Nauka), 800
-
Schlickeiser, R. 1989, ApJ, 336, 243
NASA ADS
- Schlickeiser, R., Dung, R.,
& Jackel, U. 1991, A&A, 242, L5
NASA ADS
- Shishov, V. I. 1966,
Geomagn. Aeronomy, 6, 223
- Sidorov, Yu. V., Fedoryuk, M. V.,
& Shabunin, M. I. 1982, The lectures on the theory of
complexe variable functions (Moscow: Nauka), 488
- Toptygin, I. N. 1985,
Cosmic rays in interplanetary magnetic fields
(Dordrecht: Reidel), 302
- Webb, G. M., Pantazopoulou, M., & Zank, G. P. 2000,
J. Phys. A. Math. Gen., 33, 3137
NASA ADS
- Zank, G. P., Lu, J. Y., Rice, W. K. M.,
& Webb, G. M. 1999,
Proc. 26th Intern. Cosmic Ray Conf. (Salt Lake City), 6, 312
Copyright ESO 2003


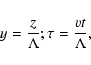
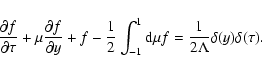
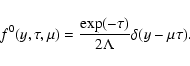
![]() and a Fourier transform in
dimensionless spatial coordinate y (Fedorov & Shakhov 1993;
Fedorov et al. 1995).
The CR distribution function can be presented
as an expansion into Legendre polynomials
and a Fourier transform in
dimensionless spatial coordinate y (Fedorov & Shakhov 1993;
Fedorov et al. 1995).
The CR distribution function can be presented
as an expansion into Legendre polynomials
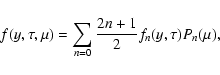

![]()


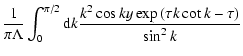
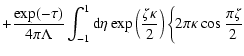
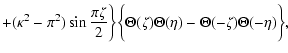
![]() is shown in
Fig. 1, where the dashed curve corresponds to unscattered particles (6),
the dotted curve accounts for scattered particles (8), and the curve 1
gives the density of all particles. One can see that the density of
unscattered particles is uniform in the region
is shown in
Fig. 1, where the dashed curve corresponds to unscattered particles (6),
the dotted curve accounts for scattered particles (8), and the curve 1
gives the density of all particles. One can see that the density of
unscattered particles is uniform in the region ![]() and
the scattered particle density decreases with y. It is worth noting that
the density equals zero for
and
the scattered particle density decreases with y. It is worth noting that
the density equals zero for ![]() in accordance with the
finite value of particle velocity.
in accordance with the
finite value of particle velocity.
![]() increases drastically from zero
to a finite value, and at
increases drastically from zero
to a finite value, and at ![]() the unscattered particle
density decays exponentially. The density of scattered particles at
the unscattered particle
density decays exponentially. The density of scattered particles at ![]() increases continuously from zero at
increases continuously from zero at ![]() ,
and after a
couple of scattering times the scattered particles dominate the distribution
of all particles, presented in Fig. 2 by curve 1.
,
and after a
couple of scattering times the scattered particles dominate the distribution
of all particles, presented in Fig. 2 by curve 1.
![]() ). In this case one can neglect the unscattered particle density (6) and the second term in expression (8), which is small because of the
exponential multiplier. Thus under condition
). In this case one can neglect the unscattered particle density (6) and the second term in expression (8), which is small because of the
exponential multiplier. Thus under condition
![]() we can obtain from
Eq. (8) the following approximate formula (the derivation of this
expression is done in Appendix A)
we can obtain from
Eq. (8) the following approximate formula (the derivation of this
expression is done in Appendix A)

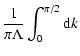
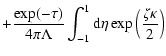
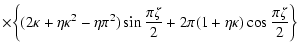


![]() and by integrating the
result from
and by integrating the
result from ![]() to
to ![]() (Earl 1994; Zank et al. 1999).
If we multiply Eq. (2) by 1,
(Earl 1994; Zank et al. 1999).
If we multiply Eq. (2) by 1, ![]() and
and
![]() respectively and
integrate over
respectively and
integrate over ![]() we obtain the following set of equations
we obtain the following set of equations


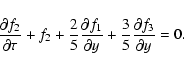






![]() function. One can see from formula (21) and from Fig. 1 (curve 3) that in
this approximation at time
function. One can see from formula (21) and from Fig. 1 (curve 3) that in
this approximation at time ![]() the particles are located only in
region
the particles are located only in
region
![]() and this region expands with
time with characteristic velocity
and this region expands with
time with characteristic velocity
![]() .
It is instructive to note
that the telegraph equation approximation corresponds to the speed of
disturbances propagation
.
It is instructive to note
that the telegraph equation approximation corresponds to the speed of
disturbances propagation
![]() (Shishov 1966;
Fisk et al. 1969;
Gombosi et al. 1993). This value of signal speed as well as the pulses,
propagating on the forward fronts of particle distribution, result from
higher harmonics neglected in the derivation of the telegraph Eq. (20). One
can see from Fig. 2, where the particle density (21) is displayed as a
function of time
(Shishov 1966;
Fisk et al. 1969;
Gombosi et al. 1993). This value of signal speed as well as the pulses,
propagating on the forward fronts of particle distribution, result from
higher harmonics neglected in the derivation of the telegraph Eq. (20). One
can see from Fig. 2, where the particle density (21) is displayed as a
function of time ![]() ,
that the particles appear in y-position
impulsively at
,
that the particles appear in y-position
impulsively at
![]() It is instructive to note that the
description based on the commonly used telegraph Eq. (20) does not
improve the accuracy of density and anisotropy calculations in comparison
with the diffusion approximation, in contrast to the modified telegraph equation
derived by Gombosi et al. (1993).
It is instructive to note that the
description based on the commonly used telegraph Eq. (20) does not
improve the accuracy of density and anisotropy calculations in comparison
with the diffusion approximation, in contrast to the modified telegraph equation
derived by Gombosi et al. (1993).




![]() and that the third harmonic is small in comparison with the first one. In
this approximation the second harmonic is proportional to the gradient of f1:
and that the third harmonic is small in comparison with the first one. In
this approximation the second harmonic is proportional to the gradient of f1:




![]() the integrand in (28) has a sharp maximum at
k=0, so it can be expanded into series near k=0 (see Appendix A). Then
integrating the obtained expression (A.11) over k we obtain formula (9). It is
interesting to note that at late times the same relationship (9) follows
both from the solution of new transport Eq. (28) and from the kinetic
equation solution (8). Thus a new transport Eq. (27) describes particle
propagation with good accuracy if the time after injection exceeds both a
mean scattering time and the time of unscattered particle propagation from
the source (
the integrand in (28) has a sharp maximum at
k=0, so it can be expanded into series near k=0 (see Appendix A). Then
integrating the obtained expression (A.11) over k we obtain formula (9). It is
interesting to note that at late times the same relationship (9) follows
both from the solution of new transport Eq. (28) and from the kinetic
equation solution (8). Thus a new transport Eq. (27) describes particle
propagation with good accuracy if the time after injection exceeds both a
mean scattering time and the time of unscattered particle propagation from
the source (
![]() ).
).

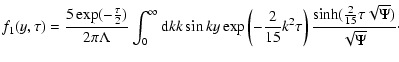






![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{f4.eps}
\end{figure}](/articles/aa/full/2003/18/aa1765/Timg87.gif)



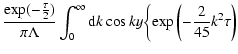
![$\displaystyle \times\biggl[\left(k^{2}+\frac{45}{4}\right)
\frac{\sinh \left(\f...
...{\sqrt{\Psi _{1}}}+
\cosh \left(\frac{2}{45}\tau \sqrt{\Psi _{1}}\right)\biggr]$](/articles/aa/full/2003/18/aa1765/img98.gif)
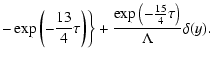

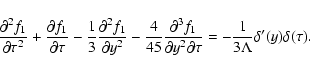

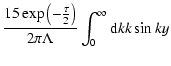
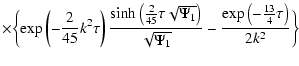
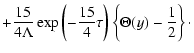
![]() takes the value somewhat below the maximal
level of
takes the value somewhat below the maximal
level of ![]() ,
obtained from the kinetic equation.
,
obtained from the kinetic equation.
![]() in contrast to the
in contrast to the
![]() value of
disturbances propagation speed in Eq. (20). Under small angle
scattering one can obtain the modified telegraph equation with the
characteristic propagation speed of
value of
disturbances propagation speed in Eq. (20). Under small angle
scattering one can obtain the modified telegraph equation with the
characteristic propagation speed of
![]() ,
which is below
the particle velocity value (Gombosi et al. 1993).
Let us transform the transport Eq. (27) in the telegraph equation
form. In order to replace a mixed derivative in (27) one can use the
diffusion equation. Differentiating (17) we can obtain the approximate
relation for the mixed derivative which appears to be proportional to the second
order time derivative of particle density. Substituting the obtained
expression into transport Eq. (27) yields
,
which is below
the particle velocity value (Gombosi et al. 1993).
Let us transform the transport Eq. (27) in the telegraph equation
form. In order to replace a mixed derivative in (27) one can use the
diffusion equation. Differentiating (17) we can obtain the approximate
relation for the mixed derivative which appears to be proportional to the second
order time derivative of particle density. Substituting the obtained
expression into transport Eq. (27) yields
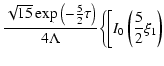
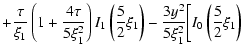
![$\displaystyle +I_{2}\left(\frac{5}{2}\xi_{1}\right)\bigg]\bigg]
\Theta\left (\tau -\sqrt{\frac{3}{5}}\left\vert y\right\vert \right)$](/articles/aa/full/2003/18/aa1765/img115.gif)
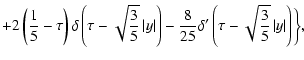

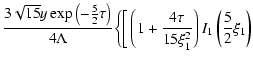
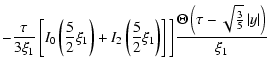
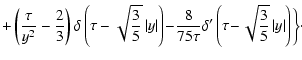

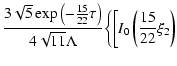
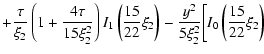
![$\displaystyle +I_{2}\left(\frac{15}{22}\xi_{2}\right)\bigg] \bigg]
\Theta \left(\tau -\sqrt{\frac{11}{5}}\left\vert y\right\vert \right)$](/articles/aa/full/2003/18/aa1765/img125.gif)
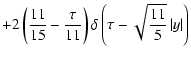
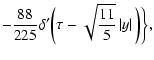

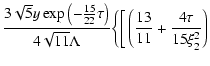
![$\displaystyle \times I_{1}\left(\frac{15}{22}\xi _{2}\right)
-\frac{\tau }{11\x...
...c{15}{22}\xi _{2}\right)+
I_{2}\left(\frac{15}{22}\xi _{2}\right)\right] \bigg]$](/articles/aa/full/2003/18/aa1765/img131.gif)
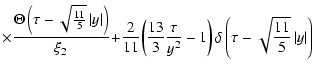
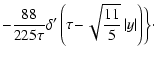
![]() , which is associated with a diffusion
coefficient in angular space
, which is associated with a diffusion
coefficient in angular space
![]() by a known relation
(Hasselmann & Wibberenz 1968;
Beeck & Wibberenz 1986; Dröge 2000)
by a known relation
(Hasselmann & Wibberenz 1968;
Beeck & Wibberenz 1986; Dröge 2000)

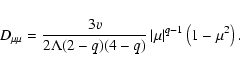
![]() where r is a heliographic coordinate, and the kinetic
equation, describing CR propagation, takes the form
where r is a heliographic coordinate, and the kinetic
equation, describing CR propagation, takes the form
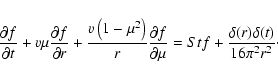
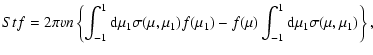



![]() and
and
![]() and integrating over
and integrating over ![]() from -1 to 1, one can obtain a set of equations for distribution function harmonics
from -1 to 1, one can obtain a set of equations for distribution function harmonics




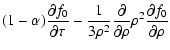
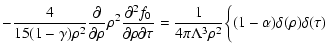
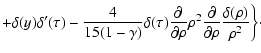
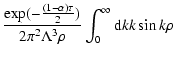
![$\displaystyle \times\exp \left(-\frac{2}{15(1-\gamma )}k^{2}\tau \right)
\biggl\{\left[ k^{2}+\frac{15}{4}(1-\alpha )(1-\gamma )\right]$](/articles/aa/full/2003/18/aa1765/img163.gif)
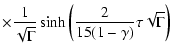
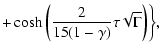
![$\displaystyle \Gamma (k)=k^{4}-\frac{15}{4}(1-\gamma )(3+2\alpha -5\gamma )k^{2}+\left[
\frac{15}{4}(1-\alpha )(1-\gamma )\right] ^{2}.$](/articles/aa/full/2003/18/aa1765/img166.gif)
![$\displaystyle f_{0}(y,\tau )=\frac{\left[ 3(1-\alpha )\right] ^{\frac{3}{2}}\ex...
... )\tau }
+3\frac{(\alpha -\gamma )\rho ^{2}}{(1-\gamma )\tau ^{2}}\right\}\cdot$](/articles/aa/full/2003/18/aa1765/img167.gif)
![]() -ray emission (Belov
et al. 2001; Pchelkin et al. 2001;
Bieber et al. 2002). It should be emphasized that
the arrival of the first relativistic protons was registered
on Earth at 10.30 UT which does not contradict a particle injection
near the Sun at 10.20 UT.
-ray emission (Belov
et al. 2001; Pchelkin et al. 2001;
Bieber et al. 2002). It should be emphasized that
the arrival of the first relativistic protons was registered
on Earth at 10.30 UT which does not contradict a particle injection
near the Sun at 10.20 UT.
![]() ). In all
cases the mean free path was selected from a condition of coincidence of the
calculated CR maximum with the moment of maximal intensity detected on the
neutron monitor Sanae (33 min after 10.20 UT of July 14, 2000). The mean
free path
). In all
cases the mean free path was selected from a condition of coincidence of the
calculated CR maximum with the moment of maximal intensity detected on the
neutron monitor Sanae (33 min after 10.20 UT of July 14, 2000). The mean
free path
![]() AU corresponds to isotropic scattering,
and
AU corresponds to isotropic scattering,
and
![]() AU is associated with the linearly anisotropic
scattering according to a decrease in
AU is associated with the linearly anisotropic
scattering according to a decrease in ![]() with increase of
scattering anisotropy.
with increase of
scattering anisotropy.
![]() coincide with the diffusion and telegraph equation descriptions. It is worth
noting that in the first order approximation relative to
coincide with the diffusion and telegraph equation descriptions. It is worth
noting that in the first order approximation relative to
![]() the
results obtained from the kinetic equation
and from the telegraph equation approach
differ from one another.
the
results obtained from the kinetic equation
and from the telegraph equation approach
differ from one another.
![]() for reasonably short distances from the particle source
(z<vt), it is not close to the boundaries of the region filled by particles.
for reasonably short distances from the particle source
(z<vt), it is not close to the boundaries of the region filled by particles.
![]()






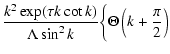
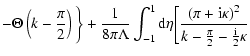
![$\displaystyle -\frac{(\pi -{\rm i}\kappa )^{2}}{
k+\frac{\pi }{2}-\frac{{\rm i}}{2}\kappa }\biggr]\exp ({\rm i}k\tau \eta ),$](/articles/aa/full/2003/18/aa1765/img194.gif)
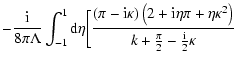
![$\displaystyle +\frac{(\pi +{\rm i}\kappa )(2-{\rm i}\eta \pi +\eta \kappa ^{2})}{
k-\frac{\pi }{2}-\frac{\rm i}{2}\kappa }\biggr]\exp ({\rm i}k\tau \eta ),$](/articles/aa/full/2003/18/aa1765/img199.gif)
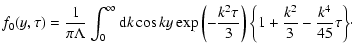
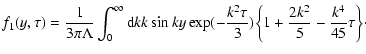

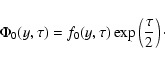




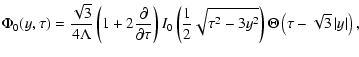
![]() can be obtained from (21) by applying an asymptotic expression of a
modified Bessel function, which is valid for large values of x(Abramowitz & Stegun 1964)
can be obtained from (21) by applying an asymptotic expression of a
modified Bessel function, which is valid for large values of x(Abramowitz & Stegun 1964)

![]() according to (B.1). Performing the Fourier-Laplace transformation of Eq. (27) one can obtain the following formula
according to (B.1). Performing the Fourier-Laplace transformation of Eq. (27) one can obtain the following formula

![]() (C.1) has two poles, so by calculating
the residual values we can obtain the relationship
(C.1) has two poles, so by calculating
the residual values we can obtain the relationship

![]() (29) becomes negative
for
k1<k<k2, where
(29) becomes negative
for
k1<k<k2, where

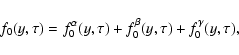
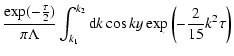
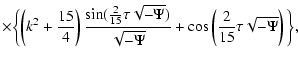
![]() .
Let us rewrite
expression (28) in the form
.
Let us rewrite
expression (28) in the form
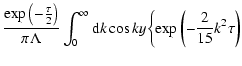
![$\displaystyle \times\biggl[ \left(k^{2}+\frac{15}{4}\right)\frac{\sinh \left(\f...
...\right)}
{\sqrt{\Psi }}+\cosh\left (\frac{2}{15}\tau \sqrt{\Psi }\right)\biggr]$](/articles/aa/full/2003/18/aa1765/img226.gif)
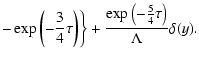
![]() .
Thus, the
relationship (31) can be rewritten as
.
Thus, the
relationship (31) can be rewritten as