Synthetic magnitudes of MR Vel resulted in J = 13.05, J-H = 0.76 and H-K = 0.53, with probable uncertainties of 0.1 mag. When using a colour excess of E(B-V) = 1.94 (Matsumoto & Mennickent 2000), we find unreddened colours of J-H = 0.15and H-K = 0.17, comparable to those observed in the SSS QR And (RX J0019.8+2156, Fender & Burnell 1996). Our finding likely indicates the presence of absorbing circumstellar material or a late-type companion. To our knowledge, these are the first infrared magnitudes and colours obtained for MR Vel ever. Therefore, it would be interesting to compare these magnitudes with future data in order to search for variability.
The combined spectrum reveals a steep blue continuum and
weak emission lines (Fig. 1). A straight-line
fit to the continuum in this region
results in a slope of
![]() ergs s-1 cm-2 Å-1/
ergs s-1 cm-2 Å-1/![]() m, which is incompatible
with a power law.
After a close inspection of the normalized spectrum
(Fig. 2), we identified lines of
neutral hydrogen (Paschen and Bracket), single ionized helium
and highly ionized oxygen.
These lines are listed in Table 1 along with
relevant spectroscopic data. No evidence of a transient
emission-line jet like those observed in H
m, which is incompatible
with a power law.
After a close inspection of the normalized spectrum
(Fig. 2), we identified lines of
neutral hydrogen (Paschen and Bracket), single ionized helium
and highly ionized oxygen.
These lines are listed in Table 1 along with
relevant spectroscopic data. No evidence of a transient
emission-line jet like those observed in H![]() by
Motch (1998) was detected. No photospheric absorptions,
such as CO bands, are observed in the spectra.
One interesting feature is the
P-Cygni profile observed in the
Paschen
by
Motch (1998) was detected. No photospheric absorptions,
such as CO bands, are observed in the spectra.
One interesting feature is the
P-Cygni profile observed in the
Paschen ![]() and Bracket
and Bracket ![]() lines (Fig. 3). The velocities found in the corresponding blueshifted
absorption wings, relative to the
emission maximum, reach up to -3000 (-1500) km s-1,
being the absorption minimum at -755 (-680) km s-1, for Paschen
lines (Fig. 3). The velocities found in the corresponding blueshifted
absorption wings, relative to the
emission maximum, reach up to -3000 (-1500) km s-1,
being the absorption minimum at -755 (-680) km s-1, for Paschen ![]() (Brackett
(Brackett ![]() ). After inspection of the data, we realized
that the difference between the maximum absorption velocity
of these lines are real, and they
cannot be due to an error in the continuum normalization.
). After inspection of the data, we realized
that the difference between the maximum absorption velocity
of these lines are real, and they
cannot be due to an error in the continuum normalization.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{rxj0925.eps} \end{figure}](/articles/aa/full/2003/16/aah4086/Timg14.gif) |
Figure 1: Flux calibrated spectrum of MR Vel. The vertical scale has been normalized to 2.03E-15 erg cm-2 s-1 Å-1. |
![\begin{figure}
\par\includegraphics[height=9cm,width=16.7cm,clip]{combined.eps} \end{figure}](/articles/aa/full/2003/16/aah4086/Timg15.gif) |
Figure 2: From up to down, J-band, K-band and H-band continuum normalized spectra for MR Vel. Emission lines are labeled. |
In the picture of the steady nuclear-burning white dwarf model,
the mass accretion rate is limited in the narrow region
around
![]()
![]() .
Since the critical accretion rate of the white dwarf
(
.
Since the critical accretion rate of the white dwarf
(
![]() )
is
)
is
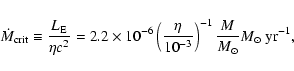 |
(1) |
| Line | Intensity | EW (Å) | FWHM (km s-1) |
O II 11334-38 |
2.2 | -2 | N/A |
| He II 11628-77 | 2.3 | -2 | N/A |
| O VI 12617 | 2.0 | N/A | N/A |
| O III 12692 | 2.2 | N/A | N/A |
| Pa |
2.4 | -5 | 367 |
Br |
1.7 | -3 | 555 |
| Br |
1.6 | -2 | 627 |
| Br |
1.5 | -2 | 560 |
| He II 16926 | 1.5 | -1 | 540 |
| Br |
1.5 | -4 | 440 |
O I 19463 |
1.3 | -9 | 564 |
| He II 19548 | 1.2 | -3 | 520 |
| Br |
1.0 | -9 | 473 |
| He II 21891 | 0.9 | -4 | 740 |
| He II 23480 | 0.7 | N/A | N/A |
A model of an accretion disk with a supercritical accretion rate was originally proposed by Abramowicz et al. (1988), as an optically thick and geometrically thick disk (e.g., Kato et al. 1998 for a review). Abramowicz et al. (1988) called the model a slim disk because of its medium thickness between a thin disk and a thick one. We refer it as a supercritical accretion disk, based on a physical viewpoint of the supercritical accretion rate.
The standard model for SSS indicates that we should consider a nearly
critical accretion in SSS systems instead of the standard
accretion disk (Shakura & Sunyaev 1973).
It is also expected that a very luminous white dwarf in
SSS strongly irradiates the accretion disk and eventually the companion
(e.g. Popham & Di Stefano
1996; Schandl et al. 1997; Meyer-Hofmeister et al. 1997;
Matsumoto & Fukue 1998; Meyer-Hofmeister et al. 1998).
These effects in SSS were investigated by Fukue
& Matsumoto (2001).
In this work, we have calculated the spectral energy distribution
(SED) for MR Vel, including the supercritical
accretion disk and the irradiation effect, and have compared
it with the observed spectrum in the range of optical-IR region
after dereddening with
E(B-V)= 1.94 (i.e. AV ![]() 5.9, Matsumoto & Mennickent 2000).
The concept and formulation of the numerical model are
described in Fukue & Matsumoto (2001), and we basically
conform the manner in calculations to Fukue & Matsumoto (2001)
in this paper.
5.9, Matsumoto & Mennickent 2000).
The concept and formulation of the numerical model are
described in Fukue & Matsumoto (2001), and we basically
conform the manner in calculations to Fukue & Matsumoto (2001)
in this paper.
The inferred intrinsic X-ray luminosity highly depends on the
model-atmosphere and gravity used in the fitting process,
but in any case, X-ray observations
and theoretical models have suggested that the white dwarf should be
extremely massive (Shimura 2000; Ebisawa et al. 2001),
although recent NLTE models of hot white dwarf atmospheres fail to
represent the complex X-ray spectrum (Motch et al. 2002).
In the following, as a working hypothesis, we assume
a blackbody SED for the central source associated with a
![]() white dwarf.
This means that we choose the WD
luminosity matching thecore-mass-luminosity relationship derived by
Iben & Tutukov (1996) for cold WDs accreting hydrogen:
white dwarf.
This means that we choose the WD
luminosity matching thecore-mass-luminosity relationship derived by
Iben & Tutukov (1996) for cold WDs accreting hydrogen:
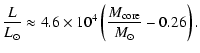 |
(2) |
An extremely small opening angle of the supercritical accretion
disk (![]() )
corresponds to a thin standard accretion disk.
According to Hanamoto et al. (2001),
)
corresponds to a thin standard accretion disk.
According to Hanamoto et al. (2001), ![]() is required to be
more than 0.3
is required to be
more than 0.3![]() for a mass-accretion rate of
for a mass-accretion rate of
![]() expected for SSS.
On the other hand, larger
expected for SSS.
On the other hand, larger ![]() brings no significant
increase of the luminosity in Rayleigh-Jeans tail of the SED.
This can constrain upper and lower limits for the distance.
brings no significant
increase of the luminosity in Rayleigh-Jeans tail of the SED.
This can constrain upper and lower limits for the distance.
For an inclination angle in the range from 45![]() to
65
to
65![]() ,
we
found that
the calculated SED based on the supercritical model described above
suggests a distance to the source between 2 and 4 kpc for a wide
range of
,
we
found that
the calculated SED based on the supercritical model described above
suggests a distance to the source between 2 and 4 kpc for a wide
range of
![]() (0.3-5).
Even in the unlikely case of
(0.3-5).
Even in the unlikely case of
![]() ,
the distance
is constrained to
,
the distance
is constrained to
![]() 5-6 kpc. A representative fitting is shown in
Fig. 4,
which is calculated for a case of
5-6 kpc. A representative fitting is shown in
Fig. 4,
which is calculated for a case of
![]() (corresponding to
(corresponding to
![]() ,
,
![]() ,
T= 7200 K)
and
,
T= 7200 K)
and
![]() .
Besides the approximations and assumptions
of our disk models, the differences between observed and theoretical
spectra
can be explained by a small error in
the dereddening and/or the
flux calibration for the optical NTT data, by
photometric orbital variability or by the use of
non-simultaneous optical-infrared data.
From the above considerations we conclude that the
distance for the source probably lies between 2 and 5 kpc.
.
Besides the approximations and assumptions
of our disk models, the differences between observed and theoretical
spectra
can be explained by a small error in
the dereddening and/or the
flux calibration for the optical NTT data, by
photometric orbital variability or by the use of
non-simultaneous optical-infrared data.
From the above considerations we conclude that the
distance for the source probably lies between 2 and 5 kpc.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{model.EPS} \end{figure}](/articles/aa/full/2003/16/aah4086/Timg38.gif) |
Figure 4:
A representative SED model of MR Vel
calculated for the
supercritical accretion case with an inclination angle of
|
Copyright ESO 2003