A&A 401, 419-428 (2003)
DOI: 10.1051/0004-6361:20030144
D. Korcáková1,2 - J. Kubát2
1 - Ústav teoretické fyziky a astrofyziky PrF MU,
Kotlárská 2, CZ-611 37 Brno, Czech Republic
2 -
Astronomický ústav, Akademie ved Ceské
republiky, CZ-251 65 Ondrejov, Czech Republic
Received 21 May 2002 / Accepted 17 January 2003
Abstract
We describe the solution of the one-dimensional radiative transfer
equation using the discontinuous finite element method.
Tests of this method prove its reliability for static media.
The static solution is then applied to the solution of the transfer
equation in a moving medium using a method which
we call here the Local
Lorentz Transformation (LLT) method.
This new method is applicable also to
non-monotonic velocity fields.
Direct solution of the radiative transfer equation in the moving medium
using the discontinuous finite element method is also presented
for cases both with and without inclusion of the effect of aberration.
All three techniques are compared and they give comparable results.
Key words: radiative transfer - methods: numerical
The solution of the equation of radiative transfer belongs to the most important problems in astrophysics. There are many methods and computer codes for static media, but there are also many problems that do not allow ignoring of the motion of a medium, like studying atmospheres of hot stars with fast stellar winds in O stars or Wolf-Rayet stars, expanding nebulae, novae, supernovae, extragalactic radio sources, and fast changes in solar prominences. Consequently, the problem of the transfer of radiation is more complicated. The reasons for this are the coefficients of emissivity and opacity, which in the case of differential motion are angle dependent.
For continuum radiation we can simply use the static equation of radiative transfer, since the opacity and emissivity coefficients change only a little within the region of the Doppler frequency shift. However, this is not true for lines. Changes of the opacity caused by the Doppler shift may be large, and we have to take it into consideration. Generally, there are two basic classes of methods for its solution, namely the solution in the observer frame (usually a frame connected with the center of a star) and the solution in the comoving frame, which is the frame connected with (usually outflowing) material. A basic review and discussion of the applicability of both classes of methods can be found in Mihalas & Kunasz (1986).
Solution of the radiative transfer equation in the comoving frame is a commonly used possibility. It takes advantage of the fact that the opacity and emissivity coefficients are not affected by motion and may be treated as in the static case (i.e., if they are isotropic for the static case then they are isotropic also in a local reference frame in a moving atmosphere). However, the transfer equation becomes more complicated due to an additional term containing the frequency derivative of the intensity. This term describes the Doppler shift of radiation. The comoving-frame transfer equation is usually solved using Feautrier variables, which introduce additional restrictions to monotonic velocity fields (see Mihalas et al. 1975,1976a,1976b,1976c; Mihalas & Kunasz 1978). Feautrier variables have also been used by Hillier (1987). In addition, Feautrier variables are not usable for the solution of the relativistic transfer equation, where characteristic rays are not symmetric (Mihalas 1980) and use of short-characteristics is more appropriate (Hauschildt 1992).
Another effect, which is usually neglected, is the effect of aberration.
The importance of aberration was discussed by Mihalas et al.
(1976b); they concluded that for stellar winds (where
![]() )
the aberration and advection effects may be safely
ignored.
This was in principle confirmed by Hauschildt et al. (1995) who
found the aberration and advection effects for novae to be negligible.
On the other hand, Hauschildt et al. (1991) showed that for
)
the aberration and advection effects may be safely
ignored.
This was in principle confirmed by Hauschildt et al. (1995) who
found the aberration and advection effects for novae to be negligible.
On the other hand, Hauschildt et al. (1991) showed that for
![]() ,
omission of aberration leads to errors larger than 50% and Baron et al. (1996) found non-negligible effects of
advection for velocities larger than
,
omission of aberration leads to errors larger than 50% and Baron et al. (1996) found non-negligible effects of
advection for velocities larger than ![]()
![]() .
Another study of the effects of aberration and advection was performed
by Peraiah (1987, 1991a), who found significant differences
in the mean intensity and flux for maximum velocities between
.
Another study of the effects of aberration and advection was performed
by Peraiah (1987, 1991a), who found significant differences
in the mean intensity and flux for maximum velocities between
![]() and
and
![]() both for planar and spherical geometry.
He also obtained changes in spectral lines (Peraiah 1991a),
but it is not clear what the real effect of aberration is.
both for planar and spherical geometry.
He also obtained changes in spectral lines (Peraiah 1991a),
but it is not clear what the real effect of aberration is.
In the first part of this paper we discuss briefly the one-dimensional equation of radiative transfer, which we will use in the subsequent parts. Here we use the slightly overlooked method of discontinuous finite elements, which has been introduced into astronomy by Castor et al. (1992), and Dykema et al. (1996). The solution of the static radiative transfer equation using this method is described in Sect. 3. In Sect. 4 we describe two new methods of solution of the one-dimensional equation of radiative transfer in moving media in a comoving frame based on the discontinuous finite elements method. The solution of the radiative transfer equation where the effect of aberration is not neglected is presented as well. In the last part we discuss the advantages and disadvantages of the method of discontinuous finite elements in these cases.
If the velocity of the medium is not very high with respect
to the observer
frame, we can neglect aberration, because the influence of the Doppler
effect is much stronger.
In this case, Eq. (3) reduces to (see Mihalas
1978, Eq. (14.99))
In the past, several classes of methods for the solution of the radiative transfer equation have been used. Possibly the most successful class of methods that have been used in a number of NLTE model atmosphere codes (e.g. Mihalas et al. 1975; Werner 1986; Hubeny 1988; Kubát 1994, 2002) is the solution of the transfer equation as a differential equation using the Feautrier (1964) method. Another class of methods is based on an integral method (see, e.g., Kalkofen 1974; Avrett & Loeser 1984).
In this paper, we deal with the in astrophysical radiative transfer slightly overlooked method of discontinuous finite elements (DFE). This method was originally developed for a study of neutron transfer by Goldin (1964). It is very similar to the finite element method, which has been used very often in various calculations in physics in the last few decades (see, e.g., Rektorys 1980). It was at first used for a solution of the radiative transfer equation by Castor et al. (1992). Further improvements and generalization of this method to more spatial dimensions were published by Dykema et al. (1996). Recently, a finite element method was used by Richling et al. (2001) for the solution of the monochromatic static radiative transfer equation in three dimensions.
The discontinuous finite element method is a generalization of the finite element method (see, e.g., Rektorys 1980). This method is based on the Galerkin method. To understand the discontinuous finite element method, we first describe briefly the Galerkin method.
Let us take a differential equation
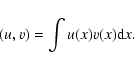 |
(8) |
Appropriate base functions for the finite element method may be
found, e.g., according to Rektorys (1980).
We section the region, where we seek the solution u, to cells.
We consider the base function to be nonzero only in a single cell.
We choose the base functions to be as simple as possible, e.g.,
polynomials or splines.
Let us assume that the subspace in a particular cell is L-dimensional,
i.e. we have L nonzero base functions wl (
![]() )
there
(
L=K/number of cells).
Then we solve the following system of algebraic equations for every
cell,
)
there
(
L=K/number of cells).
Then we solve the following system of algebraic equations for every
cell,
Contrary to the above described Galerkin method, in the discontinuous
finite element method we do not neglect the residue
![]()
| (10) |
In this section we describe the solution of Eq. (2). The method basically follows Castor et al. (1992). We present this simple case here, because we shall use this method later in a more complicated situation of moving atmosphere.
First, we introduce the discretization of the geometrical
depth
![]() .
Note that the subscript d=1 corresponds to the deepest point.
We assume a linear dependence of the intensity on the depth within
each
cell (see Fig. 1).
.
Note that the subscript d=1 corresponds to the deepest point.
We assume a linear dependence of the intensity on the depth within
each
cell (see Fig. 1).
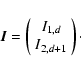 |
(19) |
| I1,D = 0. | (22) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2715f2.eps}
\end{figure}](/articles/aa/full/2003/14/aa2715/Timg67.gif) |
Figure 2: Comparison of the Feautrier method (dashed line) and the method of discontinuous finite elements (solid line) for a static planar atmosphere. |
In this section we describe the application of the method of discontinuous finite elements to the solution of the transfer equation with velocity fields, Eqs. (3) and (4).
This method is based on the fact that when we solve a radiative transfer equation in a medium, which moves with a constant uniform velocity with respect to a static observer, the static solution of the radiative transfer equation is fully sufficient. This is obviously not true if there is a velocity gradient present in the medium. However, if we split the differentially moving medium into cells with constant uniform velocities moving with respect to each other, the transfer equation inside these cells may still be considered a static one thus preserving the simplicity of a static radiative transfer Eq. (2) locally. We proceed as follows.
We split the region into cells as described in Sect. 3.1.
In every cell we assume a constant velocity of the medium.
The velocity changes only at cell boundaries.
For quantities that do not change within the cell, but which
change on cell boundaries (grid points) we use "half indexes'', e.g.,
![]() ,
which means that this cell is between grid points d and d+1.
Since we consider individual cells as local inertial frames, we must
transform both intensity and frequency at the boundaries between cells.
Transformation laws for these quantities are
,
which means that this cell is between grid points d and d+1.
Since we consider individual cells as local inertial frames, we must
transform both intensity and frequency at the boundaries between cells.
Transformation laws for these quantities are
In practice we use the same frequency points as in the static case.
We solve the Eq. (2)
for each cell for these frequency
points.
At the cell boundary, we calculate the Doppler shift of frequency,
Eq. (24),
and interpolate the intensity I2,d (Sect. 3.1 and Fig. 1) to these new "rest''
frequencies.
We tested both linear and parabolic polynomial interpolation and found
the difference at the sixth order only.
Because the equation of radiative transfer is Lorentz invariant,
we solve the static Eq. (2) in each cell using the DFE method described in Sect. 3.1,
i.e. we solve
the Eq. (17) with
![]() and
and ![]() given by (18).
The resulting intensity is given by Eq. (20).
We chose the geometrical depth as an
independent variable.
Due to the strong dependence of the opacity on frequency in a spectral
line the geometrical depth is more suitable as an independent variable
than the optical depth.
given by (18).
The resulting intensity is given by Eq. (20).
We chose the geometrical depth as an
independent variable.
Due to the strong dependence of the opacity on frequency in a spectral
line the geometrical depth is more suitable as an independent variable
than the optical depth.
We tested this method for several particular cases.
Here we show the result of calculations for a stellar wind with a
velocity expressed by the beta law (Cassinelli & Lamers 1999,
Eq. (2.3))
This method is most effective in a case where the velocity gradient is not "too large''. We simply have to guarantee that the sets of new and old frequency points at a cell boundary significantly overlap. More exactly, the frequency shift must be smaller than the Doppler halfwidth. With increasing velocity gradient the number of cells has also to increase and, consequently, one needs more computing time to solve the equation. However, for "very'' large velocity gradients we may use the Sobolev method.
The local Lorentz transformation method is extremely useful for media with small and medium velocity gradients where it enables easy and fast implementation of the velocity field while preserving the basic simplicity of a static formulation of the radiative transfer equation.
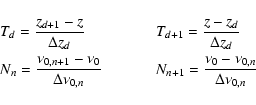
| (30) |


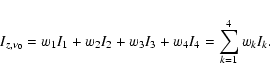 |
(31) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2715f5.eps}
\end{figure}](/articles/aa/full/2003/14/aa2715/Timg103.gif) |
Figure 5: The scheme for the expression of the jump of the intensity at the boundary of the cell (see Eq. (34)). The thick square denotes the current cell. |
We again perform a scalar product with the functions wl, i.e.
we multiply the Eq. (32) by functions wl and
integrate it over the volume of the cell,
![\begin{displaymath}\vec{I}~=~
\left(\begin{array}{c}
I_{1}\\ [2mm] I_{2}\\ [2mm]...
...,n+1})\\ [2mm]
I(z_{d+1},\nu_{0,n+1})
\end{array} \right)\cdot
\end{displaymath}](/articles/aa/full/2003/14/aa2715/img109.gif) |
(35) |
The solution is performed from deep layers to the stellar surface
to obtain the emergent intensity and in the opposite direction
for the incoming intensity.
The solution starts at the first (either uppermost or lowest) depth point
and the intensity for all frequencies is determined.
After the intensity is known for all frequencies,
we continue with the next
depth point.
Lower boundary conditions can be obtained,
e.g., from the diffusion
approximation (21) and for the upper boundary condition we
can assume, for example, no incoming radiation.
The boundary conditions for the frequency follow directly from this solution
of transfer equation.
In the first cell ![]() the change of opacity and emissivity caused
by the Doppler effect is very small, so it is sufficient to solve
the static equation there.
The intensity in a grid point
the change of opacity and emissivity caused
by the Doppler effect is very small, so it is sufficient to solve
the static equation there.
The intensity in a grid point ![]() we obtain
as in the previous case (20),
we obtain
as in the previous case (20),
In this section we describe the solution of the radiative transfer
equation with the inclusion not only of the Doppler effect, but now also
with aberration.
We solve Eq. (3),
We introduce grids
![]() ,
,
![]() ,
,
![]() .
For each cell we choose following space functions as base functions
.
For each cell we choose following space functions as base functions
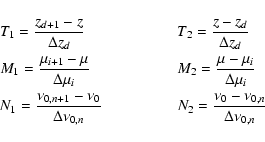
where
![]() ,
,
![]() ,
and
,
and
![]() .
We express the intensity
.
We express the intensity
| |
= | R1M1N1I111+R2M1N1I211 | |
| + R1M2N1I121+R2M2N1I221 | |||
| + R1M1N2I112+R2M1N2I212 | |||
| + R1M2N2I122+R2M2N2I222. |
As in the previous section we use following notation to enable easier description
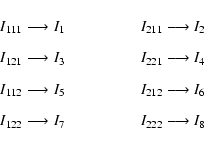
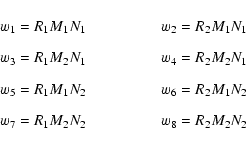
and the expression for
![]() is similar to the
case without aberration
is similar to the
case without aberration
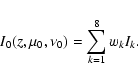 |
(39) |
After inserting this expression for the intensity into Eq. (38),
multiplying it by functions wl, and integrating
it over the volume of the cell we obtain
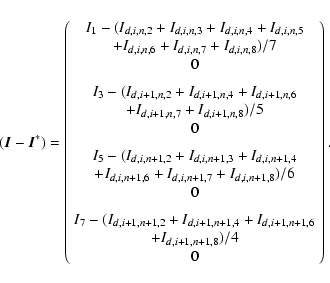 |
(41) |
We obtained a system of eight linear algebraic equations for eight
unknowns Ik that must be supplied with boundary conditions, e.g. the
diffusion approximation (21) at the lower boundary and no
incident radiation at the upper boundary.
The solution is performed in the same manner as in the simpler case without
aberration.
First, the equation is solved for all frequencies, then for all angles,
and finally, for all depth points.
The resulting intensity in a grid point ![]() we obtain
similarly as in the previous cases (20), (37),
we obtain
similarly as in the previous cases (20), (37),
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{MS2715f7.eps}\hspace*{3mm}
\includegraphics[width=7.8cm,clip]{MS2715f8.eps}
\end{figure}](/articles/aa/full/2003/14/aa2715/Timg137.gif) |
Figure 7:
Comparison of the DFE methods of solution of the radiative
transfer equation (described in Sects. 3.1 and 4)
for the case of a zero velocity gradient.
Left panel:
the dependence of the Feautrier variable u on the optical depth
for a continuum frequency.
The solid line
(denoted as static)
indicates the static solution (2), the dashed line
( LLT) denotes
solution using the local Lorentz transformation,
the fine dashed line
( with-aberration) means
solution including aberration, Eq. (38),
and the dotted line
( without-aberration) means the solution
without aberration, Eq. (26).
Note that all curves coincide.
Right panel:
the dependence of the intensity in the H |
Test calculations for the simplest case of the static radiative transfer equation have been described in the Sect. 3.1. Here we would like to discuss the choice of an independent variable for the solution of this static equation.
We found that it is better to solve this equation with geometrical depth as an independent variable. If we choose the optical depth as an independent variable, we encounter problems, since the models converge to a wrong solution. The reason lies in the numerical calculation of the system of algebraic equation, which we solve using the LU decomposition. Although the geometrical depth does not change too much throughout the atmosphere, the optical depth changes by several orders of magnitude and its use as an independent variable results in numerical inaccuracy.
We should stress that contrary to what we have said here, Castor et al.
(1992)
used the optical depth as an independent
variable.
However, they report a reduced stability for the Galerkin prescription
of the mass matrix.
They overcome the stability problems with the help of replacing the mass
matrix
![]() of the system of algebraic Eqs. (17) by
a unit matrix.
By this step one sets the term AuK-f in the
Eq. (7) to be orthonormal with respect to the chosen
set of the base functions
of the system of algebraic Eqs. (17) by
a unit matrix.
By this step one sets the term AuK-f in the
Eq. (7) to be orthonormal with respect to the chosen
set of the base functions ![]() ,
which is not generally true.
We would like to avoid such a step since in doing it we may risk
that the
method will converge to a wrong solution, because it will be stable and
we will not be able to identify errors.
,
which is not generally true.
We would like to avoid such a step since in doing it we may risk
that the
method will converge to a wrong solution, because it will be stable and
we will not be able to identify errors.
In order to perform a basic test of our methods in moving media,
we compared the solution of the static radiative transfer equation
with the solution of
the transfer equation in a moving atmosphere for the special case of a
zero velocity gradient.
All calculations have been done using the DFE method described in
Sects. 3.1 and 4.
We performed a test solution for a set frequencies from the
H![]() line assuming the Doppler profile.
Opacities have been calculated for state parameters
line assuming the Doppler profile.
Opacities have been calculated for state parameters ![]() (electron
density) and T (temperature) from an LTE model atmosphere calculated
with a code of Kubát (2002).
This model atmosphere is presented in the Table 1 (only in
electronic form).
Results of these calculations are shown in Fig. 7.
In the left panel there is a dependence of the Feautrier variable u on
an optical depth in four cases - static equation of radiative
transfer, equation written in local frequency, equation including
aberration, and calculation using local Lorentz transformation.
As we can see, all curves coincide, which means that the basic algorithm
of the solution of the transfer equation is correct. This result is supported also by a profile of the H
(electron
density) and T (temperature) from an LTE model atmosphere calculated
with a code of Kubát (2002).
This model atmosphere is presented in the Table 1 (only in
electronic form).
Results of these calculations are shown in Fig. 7.
In the left panel there is a dependence of the Feautrier variable u on
an optical depth in four cases - static equation of radiative
transfer, equation written in local frequency, equation including
aberration, and calculation using local Lorentz transformation.
As we can see, all curves coincide, which means that the basic algorithm
of the solution of the transfer equation is correct. This result is supported also by a profile of the H![]() line
emerging from this model atmosphere.
line
emerging from this model atmosphere.
In Fig. 8 we plotted H![]() line profiles for a
nonzero velocity gradient.
The velocity field is described by the beta law (25) with
the terminal velocity
line profiles for a
nonzero velocity gradient.
The velocity field is described by the beta law (25) with
the terminal velocity
![]() and the velocity in the
photosphere
and the velocity in the
photosphere
![]() .
The H
.
The H![]() line profile is computed for the same condition as in the
previous case.
Three situations described in preceding sections are shown in
Fig. 8 -
the local Lorentz transformation, discontinuous
finite element method with aberration, and without it.
line profile is computed for the same condition as in the
previous case.
Three situations described in preceding sections are shown in
Fig. 8 -
the local Lorentz transformation, discontinuous
finite element method with aberration, and without it.
The profiles shown are in a comoving frame.
For comparison, we plotted also the static solution.
We can see small deviation between the LLT method and methods using the
equation of the radiative transfer written in comoving frame.
The reason for it is in the assumption of a constant velocity in the
cell.
We can influence this deviation by
changing the density of the geometrical depth grid,
which is discussed later.
On the other hand, results obtained with the inclusion of aberration
and without it are in a good agreement.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2715f9.eps}
\end{figure}](/articles/aa/full/2003/14/aa2715/Timg139.gif) |
Figure 8: The dependence of the intensity on frequency in the case of a stellar wind of B stars. The solid line indicates the static solution, Eq. (2), the dashed line the solution using the local Lorentz transformation, the fine dashed line the solution including aberration, Eq. (38), and the dotted line the solution without aberration, Eq. (26). |
In order to see the maximum possible effect of aberration, we solved the
transfer equation for a small value of ![]() .
For this case, we obtained a small difference between the solution
including aberration and without it (cf. Fig. 9)
as expected.
Bearing in mind that no effect of aberration was found in the previous
section, we may state that
in the region of validity of Eqs. (38) and (26),
i.e., in non-relativistic velocity fields, we can
safely neglect aberration and use the simpler Eq. (26)
in accordance with previous results of Mihalas & Hummer (1976b).
.
For this case, we obtained a small difference between the solution
including aberration and without it (cf. Fig. 9)
as expected.
Bearing in mind that no effect of aberration was found in the previous
section, we may state that
in the region of validity of Eqs. (38) and (26),
i.e., in non-relativistic velocity fields, we can
safely neglect aberration and use the simpler Eq. (26)
in accordance with previous results of Mihalas & Hummer (1976b).
The grid tests show a linear dependence of the computing time
on the number of depth points
(see Fig. 10, left panel).
In
the right panel
we
plotted the dependence of the accuracy on the
number of depth grid points.
As we can see, the optimum number of depth points is about one hundred.
For this choice the solution is accurate enough and the computing time
is not too high.
For the velocity field, introduced before, the dependence of computing
time on the number of grid points is linear, too
(see Fig. 11, left panel).
It is necessary to take enough frequency grid points in the
dynamic
case, because we solve the differential equation with respect to the
variable ![]() now (see Fig. 11, right panel).
We performed the calculations with the same number of grid points in the
geometrical grid and in the frequency grid in the line (D=N=100).
now (see Fig. 11, right panel).
We performed the calculations with the same number of grid points in the
geometrical grid and in the frequency grid in the line (D=N=100).
In this paper we studied an application of the discontinuous finite element method for the solution of the radiative transfer equation both for static and differentially moving media.
First, we solved the static equation. We confirmed the fact that the discontinuous finite element method is comparable to the standard Feautrier method in the static case (Fig. 2).
Using the DFE method for the static case we developed a new method for the solution of the radiative transfer equation in moving media, which uses the Lorentz transformation of intensity and frequency between subsequent cells. Since this method uses local inertial frames we call it the local Lorentz transformation method. This method takes advantage of the possibility of a discontinuity at the cell boundary, which in this case comes from the Lorentz transformation.
We solved the transfer equation using the DFE method in the comoving frame. First, we neglected aberration and then we solved it more exactly including both the Doppler shift and aberration. Results of both methods are in good agreement, see Figs. 7 and 8.
In the region of validity of these equations (in non-relativistic velocity fields) it is not necessary to account for aberration, as we expected. This enables faster calculations, since one has to solve the set of only four algebraic equations instead of eight. On the other hand, if we aim at a more precise study of the radiation field, the possibility of taking aberration into account may become very useful.
In addition, we found that it is better to solve these equations with geometrical depth as an independent variable, since choosing the optical depth as an independent variable causes stability problems.
Another important point is a sufficiently fine frequency grid to enable good line profile resolution. If we do not resolve the line sufficiently, we obtain wrong line profiles.
The method of discontinuous finite elements may be applied to the solution of rather complex radiative transfer problems both in static and moving media. We tested it on a problem of expanding atmospheres of hot B stars. However, using this method in other types of moving media is possible as well. We plan to employ our results in future studies of Be stars.
Acknowledgements
The authors would like to thank the referee for valuable comments on the manuscript. This research has made use of NASA's Astrophysics Data System. This work was supported by a grant GA CR 205/01/0656 and by projects K2043105 and AV 0Z1 003909.
| d | z(d) | T(d) |
|
d | z(d) | T(d) |
|
| [cm] | [K] | [cm-3] | [cm] | [K] | [cm-3] | ||
| 1 | 2.2862507E+11 | 10869.33 | 1.2087334E+08 | 51 | 2.2725908E+11 | 11798.41 | 3.5495587E+13 |
| 2 | 2.2859749E+11 | 10871.11 | 1.5565563E+08 | 52 | 2.2723026E+11 | 11914.26 | 4.5219122E+13 |
| 3 | 2.2856988E+11 | 10872.91 | 2.0052332E+08 | 53 | 2.2720105E+11 | 12068.55 | 5.7414772E+13 |
| 4 | 2.2854223E+11 | 10874.71 | 2.5839916E+08 | 54 | 2.2717131E+11 | 12270.27 | 7.2621213E+13 |
| 5 | 2.2851456E+11 | 10876.52 | 3.3305214E+08 | 55 | 2.2714089E+11 | 12528.18 | 9.1470967E+13 |
| 6 | 2.2848688E+11 | 10878.34 | 4.2934243E+08 | 56 | 2.2710964E+11 | 12849.62 | 1.1471892E+14 |
| 7 | 2.2845919E+11 | 10880.16 | 5.5353549E+08 | 57 | 2.2707735E+11 | 13240.32 | 1.4328346E+14 |
| 8 | 2.2843149E+11 | 10881.97 | 7.1370837E+08 | 58 | 2.2704383E+11 | 13703.47 | 1.7833501E+14 |
| 9 | 2.2840379E+11 | 10883.77 | 9.2026996E+08 | 59 | 2.2700886E+11 | 14240.48 | 2.2141124E+14 |
| 10 | 2.2837608E+11 | 10885.55 | 1.1866316E+09 | 60 | 2.2697219E+11 | 14851.56 | 2.7455037E+14 |
| 11 | 2.2834839E+11 | 10887.31 | 1.5300680E+09 | 61 | 2.2693356E+11 | 15535.93 | 3.4030908E+14 |
| 12 | 2.2832070E+11 | 10889.04 | 1.9728199E+09 | 62 | 2.2689270E+11 | 16290.47 | 4.2150812E+14 |
| 13 | 2.2829302E+11 | 10890.72 | 2.5435123E+09 | 63 | 2.2684940E+11 | 17113.95 | 5.2092714E+14 |
| 14 | 2.2826536E+11 | 10892.36 | 3.2789661E+09 | 64 | 2.2680352E+11 | 18003.13 | 6.4184323E+14 |
| 15 | 2.2823772E+11 | 10893.95 | 4.2265177E+09 | 65 | 2.2675499E+11 | 18952.82 | 7.8885477E+14 |
| 16 | 2.2821010E+11 | 10895.49 | 5.4469899E+09 | 66 | 2.2670373E+11 | 19961.21 | 9.6801721E+14 |
| 17 | 2.2818252E+11 | 10896.97 | 7.0184887E+09 | 67 | 2.2664966E+11 | 21036.43 | 1.1863688E+15 |
| 18 | 2.2815497E+11 | 10898.38 | 9.0412928E+09 | 68 | 2.2659261E+11 | 22192.59 | 1.4518842E+15 |
| 19 | 2.2812747E+11 | 10899.70 | 1.1644098E+10 | 69 | 2.2653238E+11 | 23450.71 | 1.7733060E+15 |
| 20 | 2.2810002E+11 | 10900.88 | 1.4992139E+10 | 70 | 2.2646867E+11 | 24833.30 | 2.1604747E+15 |
| 21 | 2.2807264E+11 | 10901.84 | 1.9297694E+10 | 71 | 2.2640111E+11 | 26364.98 | 2.6243590E+15 |
| 22 | 2.2804532E+11 | 10902.44 | 2.4833720E+10 | 72 | 2.2632926E+11 | 28071.95 | 3.1771988E+15 |
| 23 | 2.2801808E+11 | 10902.53 | 3.1951684E+10 | 73 | 2.2625257E+11 | 29981.45 | 3.8328005E+15 |
| 24 | 2.2799092E+11 | 10902.03 | 4.1104624E+10 | 74 | 2.2617042E+11 | 32123.75 | 4.6068802E+15 |
| 25 | 2.2796385E+11 | 10900.97 | 5.2877084E+10 | 75 | 2.2608201E+11 | 34535.64 | 5.5183242E+15 |
| 26 | 2.2793687E+11 | 10899.61 | 6.8023408E+10 | 76 | 2.2598631E+11 | 37271.26 | 6.5926417E+15 |
| 27 | 2.2790998E+11 | 10898.41 | 8.7516950E+10 | 77 | 2.2588178E+11 | 40401.01 | 7.8689375E+15 |
| 28 | 2.2788316E+11 | 10897.91 | 1.1261283E+11 | 78 | 2.2576656E+11 | 43881.84 | 9.4007882E+15 |
| 29 | 2.2785642E+11 | 10898.67 | 1.4492799E+11 | 79 | 2.2563988E+11 | 47382.47 | 1.1278833E+16 |
| 30 | 2.2782974E+11 | 10901.14 | 1.8654342E+11 | 80 | 2.2550264E+11 | 50646.24 | 1.3655364E+16 |
| 31 | 2.2780310E+11 | 10905.84 | 2.4013307E+11 | 81 | 2.2535622E+11 | 53737.15 | 1.6662339E+16 |
| 32 | 2.2777650E+11 | 10913.35 | 3.0912736E+11 | 82 | 2.2520149E+11 | 56787.39 | 2.0422591E+16 |
| 33 | 2.2774991E+11 | 10924.34 | 3.9791981E+11 | 83 | 2.2503875E+11 | 59889.69 | 2.5085568E+16 |
| 34 | 2.2772333E+11 | 10939.45 | 5.1213412E+11 | 84 | 2.2486796E+11 | 63106.12 | 3.0837464E+16 |
| 35 | 2.2769673E+11 | 10959.12 | 6.5897143E+11 | 85 | 2.2468887E+11 | 66483.65 | 3.7905999E+16 |
| 36 | 2.2767009E+11 | 10981.80 | 8.4778709E+11 | 86 | 2.2450106E+11 | 70063.15 | 4.6565851E+16 |
| 37 | 2.2764376E+11 | 10745.77 | 1.1152910E+12 | 87 | 2.2430399E+11 | 73884.18 | 5.7145280E+16 |
| 38 | 2.2761763E+11 | 10829.46 | 1.4273560E+12 | 88 | 2.2409699E+11 | 77987.71 | 7.0033853E+16 |
| 39 | 2.2759129E+11 | 10929.20 | 1.8242781E+12 | 89 | 2.2387926E+11 | 82417.70 | 8.5691233E+16 |
| 40 | 2.2756469E+11 | 11037.59 | 2.3300047E+12 | 90 | 2.2364989E+11 | 87221.97 | 1.0465732E+17 |
| 41 | 2.2753782E+11 | 11148.33 | 2.9755770E+12 | 91 | 2.2340781E+11 | 92452.26 | 1.2756469E+17 |
| 42 | 2.2751070E+11 | 11255.31 | 3.8015103E+12 | 92 | 2.2315185E+11 | 98162.81 | 1.5515582E+17 |
| 43 | 2.2748332E+11 | 11352.59 | 4.8608780E+12 | 93 | 2.2288064E+11 | 104406.52 | 1.8831074E+17 |
| 44 | 2.2745573E+11 | 11434.12 | 6.2236334E+12 | 94 | 2.2259275E+11 | 111227.09 | 2.2809544E+17 |
| 45 | 2.2742798E+11 | 11495.12 | 7.9815046E+12 | 95 | 2.2228665E+11 | 118644.74 | 2.7585136E+17 |
| 46 | 2.2740010E+11 | 11536.20 | 1.0251265E+13 | 96 | 2.2196086E+11 | 126638.05 | 3.3334260E+17 |
| 47 | 2.2737213E+11 | 11567.58 | 1.3173932E+13 | 97 | 2.2161412E+11 | 135133.44 | 4.0294841E+17 |
| 48 | 2.2734408E+11 | 11602.42 | 1.6919765E+13 | 98 | 2.2124550E+11 | 144013.67 | 4.8785993E+17 |
| 49 | 2.2731593E+11 | 11649.40 | 2.1701062E+13 | 99 | 2.2085454E+11 | 153151.40 | 5.9221375E+17 |
| 50 | 2.2728761E+11 | 11712.65 | 2.7785210E+13 | 100 | 2.2044116E+11 | 162451.27 | 7.2115492E+17 |