Once the sky background
![]() has been estimated, the flux per
square arcsecond and per unit time is given by
has been estimated, the flux per
square arcsecond and per unit time is given by
![]() ,
where p is the detector's scale (arcsec pix-1) and
,
where p is the detector's scale (arcsec pix-1) and
![]() is
the exposure time (in seconds). The instrumental sky surface brightness
is then defined as
is
the exposure time (in seconds). The instrumental sky surface brightness
is then defined as
The next step one needs to perform to get the final sky surface brightness
is to convert the instrumental magnitudes to the standard UBVRI photometric
system. Following the prescriptions by Pilachowski et al. (1989),
the sky brightness is calibrated without correcting the measured flux by
atmospheric extinction, since the effect is actually taking place mostly
in the atmosphere itself. This is of course not true for the
contribution coming from faint stars, galaxies and the zodiacal light, which
however account for a minor fraction of the whole effect, airglow being the
prominent source of night sky emission in dark astronomical sites.
The reader is referred to Krisciunas (1990) for a more detailed
discussion of this point; here we add only that this practically
corresponds to set to zero the airmass of the observed sky area in the
calibration equation. Therefore, if
![]() ,
,
![]() are the calibrated
and instrumental sky magnitudes, M*, m* are the corresponding values
for a photometric standard star observed at airmass z*, and
are the calibrated
and instrumental sky magnitudes, M*, m* are the corresponding values
for a photometric standard star observed at airmass z*, and ![]() is
the extinction coefficient, we have that
is
the extinction coefficient, we have that
![]()
![]() .
This
relation can be rewritten in a more general way as
.
This
relation can be rewritten in a more general way as
![]() ,
where m0 is the photometric
zeropoint in a given passband and
,
where m0 is the photometric
zeropoint in a given passband and ![]() is the colour term in that
passband for the color
is the colour term in that
passband for the color
![]() .
For example, in the case of B filter,
this relation can be written as
.
For example, in the case of B filter,
this relation can be written as
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f2.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg37.gif) |
Figure 2: UBVRI photometric zeropoints for FORS1 during the time range covered by sky brightness measurements presented in this work (vertical dotted lines). The thick segments plotted on the lower diagram indicate the presence of sky brightness data, while the arrows in the upper part of the figure correspond to some relevant events. A) water condensation on main mirror of UT1-Antu. B) UT1-Antu main mirror re-aluminisation after the water condensation event. C) FORS1 moved from UT1-Antu to UT3-Melipal. Plotted zeropoints have been corrected for extinction and colour terms using average values (see Appendix A). |
In the case of FORS1, observations of
photometric standard fields (Landolt 1992) are regularly obtained as part
of the calibration plan; typically one to three fields are observed during
each service mode night. The photometric zeropoints were derived from these
observations by means of a semi-automatic procedure, assuming constant
extinction coefficients and colour terms. For a more detailed discussion on
these parameters, the reader is referred to Appendix A,
where we show that this is a reasonable assumption.
Figure 2 shows that, with the exception of a few cases,
Paranal is photometrically stable, being the rms zeropoint fluctuation
![]() 0.03 mag in U and
0.03 mag in U and
![]() 0.02 mag in all other
passbands.
Three clear jumps are visible in Fig. 2, all basically
due to physical changes in the main mirror of the telescope. Besides
these sudden variations, we have detected a slow decrease in the efficiency
which is clearly visible in the first 10 months and is most probably
due to aluminium oxidation and dust deposition. The efficiency loss
appears to be linear in time, with a rate steadily decreasing from blue to
red passbands, being 0.13 mag yr-1 in U and 0.05 mag yr-1 in I.
To allow for a proper compensation of these effects, we have divided the whole
time range in four different periods, in which we have used a linear least
squares fit to the zero points obtained in each band during photometric nights
only. This gives a handy description of the overall system efficiency which
is easy to implement in an automatic calibration procedure.
0.02 mag in all other
passbands.
Three clear jumps are visible in Fig. 2, all basically
due to physical changes in the main mirror of the telescope. Besides
these sudden variations, we have detected a slow decrease in the efficiency
which is clearly visible in the first 10 months and is most probably
due to aluminium oxidation and dust deposition. The efficiency loss
appears to be linear in time, with a rate steadily decreasing from blue to
red passbands, being 0.13 mag yr-1 in U and 0.05 mag yr-1 in I.
To allow for a proper compensation of these effects, we have divided the whole
time range in four different periods, in which we have used a linear least
squares fit to the zero points obtained in each band during photometric nights
only. This gives a handy description of the overall system efficiency which
is easy to implement in an automatic calibration procedure.
| Site | Year | U-B | B-V | V-R | V-I | Reference |
| Cerro Tololo | 1987-8 | -0.7 | +0.9 | +0.9 | +1.9 | Walker (1987, 1988a) |
| La Silla | 1978 | - | +1.1 | +0.9 | +2.3 | Mattila et al. (1996) |
| Calar Alto | 1990 | -0.5 | +1.1 | +0.9 | +2.8 | Leinert et al. (1995) |
| La Palma | 1994-6 | -0.7 | +0.8 | +0.9 | +1.9 | Benn & Ellison (1998) |
| Paranal | 2000-1 | -0.4 | +1.0 | +0.8 | +1.9 | this work |
To derive the colour correction included in the calibration equation one needs
to know the sky colours
![]() .
In principle
.
In principle
![]() can be computed
from the instrumental magnitudes, provided that the data which correspond
to the two passbands used for the given colour are taken closely in time.
In fact, the sky brightness is known to have quite a strong time evolution
even in moonless nights and far from twilight (Walker 1988b; Pilachowski et al. 1989; Krisciunas 1990; Leinert et al. 1998) and using magnitudes obtained
in different conditions would lead to wrong colours. On the other hand, very
often FORS1 images are taken in rather long sequences, which make use of
the same filter; for this very reason it is quite rare to have
close-in-time multi-band observations. Due to this fact and to allow for a
general and uniform approach, we have decided to use constant sky colours for the
colour correction. In fact, the colour terms are small, and even large errors on
the colours produce small variations in the corresponding colour correction.
can be computed
from the instrumental magnitudes, provided that the data which correspond
to the two passbands used for the given colour are taken closely in time.
In fact, the sky brightness is known to have quite a strong time evolution
even in moonless nights and far from twilight (Walker 1988b; Pilachowski et al. 1989; Krisciunas 1990; Leinert et al. 1998) and using magnitudes obtained
in different conditions would lead to wrong colours. On the other hand, very
often FORS1 images are taken in rather long sequences, which make use of
the same filter; for this very reason it is quite rare to have
close-in-time multi-band observations. Due to this fact and to allow for a
general and uniform approach, we have decided to use constant sky colours for the
colour correction. In fact, the colour terms are small, and even large errors on
the colours produce small variations in the corresponding colour correction.
For this purpose we have used color-uncorrected sky brightness values obtained
in dark time, at airmass ![]() and at a time distance from the twilights
and at a time distance from the twilights
![]() hours and estimated the typical value as the average.
The corresponding colours are shown in Table 2, where they are
compared with those obtained at other observatories. As one can see, B-Vand V-R show a small scatter between different observatories, while U-B
and V-I are rather dispersed.
In particular, V-I spans almost a magnitude, the value reported for Calar
Alto being the reddest. This is due to the fact that the Calar Alto sky in Iappears to be definitely brighter than in all other listed sites.
hours and estimated the typical value as the average.
The corresponding colours are shown in Table 2, where they are
compared with those obtained at other observatories. As one can see, B-Vand V-R show a small scatter between different observatories, while U-B
and V-I are rather dispersed.
In particular, V-I spans almost a magnitude, the value reported for Calar
Alto being the reddest. This is due to the fact that the Calar Alto sky in Iappears to be definitely brighter than in all other listed sites.
Now, given the color terms reported in Table A.2, the color
corrections
![]() turn out to be -0.02
turn out to be -0.02 ![]() 0.02,
-0.09
0.02,
-0.09 ![]() 0.02, +0.04
0.02, +0.04 ![]() 0.01, +0.02
0.01, +0.02 ![]() 0.01 and -0.08
0.01 and -0.08 ![]() 0.02 in U,
B, V, R and I respectively. The uncertainties were estimated from the
dispersion on the computed average colours, which is
0.02 in U,
B, V, R and I respectively. The uncertainties were estimated from the
dispersion on the computed average colours, which is
![]() 0.3 for all
passbands.
We emphasize that this rather large value is not due to measurement errors,
but rather to the strong intrinsic variations shown by the sky brightness,
which we will discuss in detail later on. We also warn the reader that the
colour corrections computed assuming dark sky colours are not necessarily
correct under other conditions, when the night sky emission is strongly
influenced by other sources, like Sun and moon. At any rate, colour
variations of 1 mag would produce a change in the calibrated magnitude of
0.3 for all
passbands.
We emphasize that this rather large value is not due to measurement errors,
but rather to the strong intrinsic variations shown by the sky brightness,
which we will discuss in detail later on. We also warn the reader that the
colour corrections computed assuming dark sky colours are not necessarily
correct under other conditions, when the night sky emission is strongly
influenced by other sources, like Sun and moon. At any rate, colour
variations of 1 mag would produce a change in the calibrated magnitude of
![]() 0.1 mag in the worst case.
0.1 mag in the worst case.
Due to the increased depth of the emitting layers, the sky becomes inherently
brighter for growing zenith distances (see for example Garstang 1989;
Leinert et al. 1998). In order to compare and/or combine together sky brightness
estimates obtained at different airmasses, one needs to take into account this
effect. The law we have adopted for the airmass compensation and its ability
to reproduce the observed data are discussed in Appendix C
(see Eq. (C.3)).
After including this correction in the calibration equation and neglecting
the error on X, we have computed the global rms error on the estimated sky
brightness in the generic passband as follows:
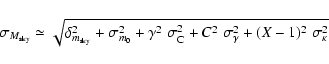 |
(2) |
Copyright ESO 2003