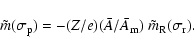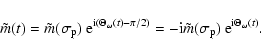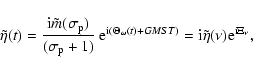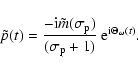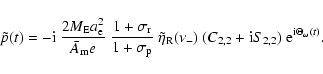Up: Polar motions equivalent to mantle
Subsections
The prograde semidiurnal nutations arise primarily from the direct
action of the (2,1) tidal potential on the Earth's triaxial structure.
Triaxiality, i.e., inequality of the two principal equatorial moments
of inertia A and B, is characterized by the parameter e':
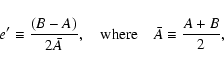 |
(47a) |
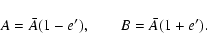 |
(47b) |
The geopotential coefficients C2,2 and S2,2 are a
reflection of triaxiality and are related to e' through
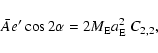 |
(48a) |
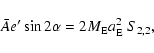 |
(48b) |
where 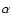 is the longitude of the direction of the axis of
maximum equatorial moment of inertia. The numbers given by
Bretagnon et al. (1997) lead to
is the longitude of the direction of the axis of
maximum equatorial moment of inertia. The numbers given by
Bretagnon et al. (1997) lead to
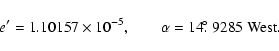 |
(49) |
We define, for later convenience, the complex parameter
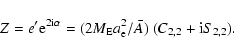 |
(50) |
Contributions to the prograde semidiurnal nutations arise
from the appearance of triaxiality through
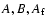 ,
and
,
and 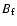 in the equatorial components of the angular momentum vectors
in the equatorial components of the angular momentum vectors 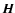 and
and
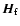 .
In a
coordinate system with its axes along the principal axes of the
inertia tensor, the equatorial components of
.
In a
coordinate system with its axes along the principal axes of the
inertia tensor, the equatorial components of 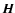 are, for the
triaxial Earth,
are, for the
triaxial Earth,
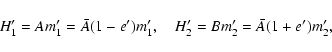 |
(51a) |
![\begin{displaymath}\tilde H'(t) = H_1'(t)+{\rm i}H_2'(t)=\bar A~[~\tilde m'(t) -e'\tilde m'^*(t)].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img245.gif) |
(51b) |
In reality, the equatorial principal axes make an angle 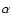 to the
axes of the generally used terrestrial reference frame,
and so
to the
axes of the generally used terrestrial reference frame,
and so
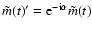 ,
,
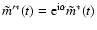 ,
and
,
and
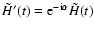 ,
as may be readily seen. It follows then
that
,
as may be readily seen. It follows then
that
![\begin{displaymath}\tilde H(t)= \bar A~[\tilde m(t)-Z~\tilde m^*(t)~ ].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img249.gif) |
(52) |
If the core is triaxial,
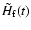 also contains triaxiality terms:
also contains triaxiality terms:
The meaning of the symbols used here should be obvious. In using
the same angle 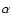 here as in the case of
here as in the case of
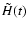 ,
we are assuming
that the principal axes of the core have the same directions as
those of the whole Earth, which seems the most likely scenario on
physical grounds.
,
we are assuming
that the principal axes of the core have the same directions as
those of the whole Earth, which seems the most likely scenario on
physical grounds.
The triaxiality terms appearing through the expressions (52) and (53) had not been
included in the dynamical equations in the earlier sections, as
the triaxiality contributions to the nutations considered there
were far below the 0.1 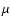 asbecause of the weakness of
the driving potentials of degree >2. With the inclusion of these
terms here, the dynamical Eqs. (29) get modified to
asbecause of the weakness of
the driving potentials of degree >2. With the inclusion of these
terms here, the dynamical Eqs. (29) get modified to
where
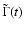 is the full torque due to the (2,1) potential,
containing both prograde and retrograde diurnal components.
is the full torque due to the (2,1) potential,
containing both prograde and retrograde diurnal components.
Consider now the frequency domain version of the above equations,
corresponding to a spectral component having the time
dependence
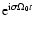 .
Noting that the amplitude
of the term in
.
Noting that the amplitude
of the term in
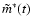 which has this time dependence is
which has this time dependence is
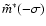 ,
and similarly for
,
and similarly for
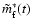 ,
one sees that the equations
are:
,
one sees that the equations
are:
It is evident that these equations couple the amplitude of any
prograde wobble (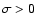 )
to that of the corresponding retrograde
wobble with frequency
)
to that of the corresponding retrograde
wobble with frequency 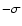 .
.
It is to be expected that the triaxiality terms in Eqs. (55) will lead to small increments to the frequencies of the free
wobbles. These increments are of the second order in triaxiality,
as may be shown very generally from the structure of these
equations. For an elementary
illustration, consider the rigid Earth, whose free wobbles are
governed by the equation
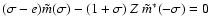 ,
which is the relevant special case of (55a). On taking its complex
conjugate and making the replacement
,
which is the relevant special case of (55a). On taking its complex
conjugate and making the replacement
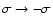 ,
one obtains a
second equation relating
,
one obtains a
second equation relating
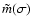 and
and
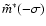 .
This pair of equations
yields the secular equation
.
This pair of equations
yields the secular equation
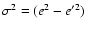 ,
where e'=|Z|. Thus
the change in the Chandler eigenfrequency due to triaxiality is from e to
e(1-e'2/2e2), to the lowest order in the triaxiality.
Given the magnitudes of e and e', the fractional change is seen
to be of the order of 10-5, which is much too small be of
interest. For the Earth with a fluid core, a similar procedure
starting with both the Eqs. (55) and their complex conjugates
with the sign of
,
where e'=|Z|. Thus
the change in the Chandler eigenfrequency due to triaxiality is from e to
e(1-e'2/2e2), to the lowest order in the triaxiality.
Given the magnitudes of e and e', the fractional change is seen
to be of the order of 10-5, which is much too small be of
interest. For the Earth with a fluid core, a similar procedure
starting with both the Eqs. (55) and their complex conjugates
with the sign of 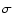 reversed, leads to a similar result also for
the second eigenfrequency associated with the free core nutation.
reversed, leads to a similar result also for
the second eigenfrequency associated with the free core nutation.
Moving on now to forced prograde diurnal wobbles due to the (2,1) potential, it is advantageous, in view of their coupling to the
retrograde diurnals, to express the potential in the form employed
by Mathews et al. (1991) in their treatment of the retrograde
diurnal wobbles:
![\begin{displaymath}\phi^{(2,1)}({\vec r};t) =
-\Omega_0^2\left[~\phi_1(t) xz+\phi_2(t) yz~\right].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img273.gif) |
(56) |
To obtain the torque due to
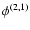 ,
it is simplest to start
with (56) reexpressed in the principal axis frame before evaluation
of the relevant integrals. The components of the torque can then be
transformed back to the original frame. The result, written down
for
,
it is simplest to start
with (56) reexpressed in the principal axis frame before evaluation
of the relevant integrals. The components of the torque can then be
transformed back to the original frame. The result, written down
for
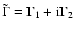 ,
is
,
is
![\begin{displaymath}\tilde\Gamma= -{\rm i}\bar A\Omega_0^2\ \left[~e\tilde\phi(t)+Z\tilde\phi^*(t)~\right].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img276.gif) |
(57) |
Higher order terms which are irrelevant in the present context
have been dropped.
For a spectral component of the potential (56) with angular
frequency 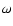 ,
,
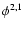 is proportional to
is proportional to
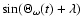 ,
,
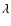 being the longitude, according to the Cartwright-Tayler
convention. This is ensured by taking the spectral components of
being the longitude, according to the Cartwright-Tayler
convention. This is ensured by taking the spectral components of 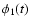 and
and 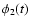 to be
to be
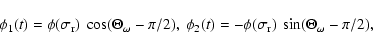 |
(58) |
with
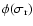 real and
real and
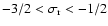 .
The complex
quantities
.
The complex
quantities
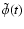 and
and
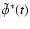 are now
are now
The torque (57) becomes now
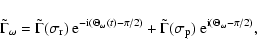 |
(60) |
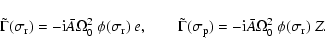 |
(61) |
On using (60), the solution of Eqs. (54) is seen to have the
form
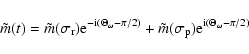 |
(62) |
together with a similar expression for
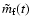 .
.
We can now specialize Eqs. (55) to the case of prograde
wobbles by setting
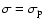 and
and
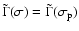 and introducing from Eqs. (31) the expressions
and introducing from Eqs. (31) the expressions
noting that
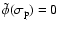 since the potential
is strictly retrograde. We thus obtain the wobble equations for
since the potential
is strictly retrograde. We thus obtain the wobble equations for
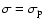 in explicit form as
in explicit form as
Now,
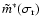 and
and
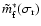 relate to the retrograde diurnal wobbles.
The triaxiality parts of the angular momenta of the Earth and its
core, which are the source of the terms containing these quantities
in the above equations, are thus seen to couple the prograde
diurnal wobbles to the retrograde ones. Thus the mechanism through
which the resonances in the latter get to affect the prograde
semidiurnal nutations becomes transparent.
relate to the retrograde diurnal wobbles.
The triaxiality parts of the angular momenta of the Earth and its
core, which are the source of the terms containing these quantities
in the above equations, are thus seen to couple the prograde
diurnal wobbles to the retrograde ones. Thus the mechanism through
which the resonances in the latter get to affect the prograde
semidiurnal nutations becomes transparent.
In the coefficients of
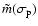 and
and
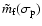 in Eqs. (64),
in Eqs. (64),
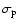 is close to 1 while all other quantities except
is close to 1 while all other quantities except
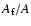 are
of
are
of
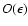 .
Substituting for
.
Substituting for
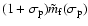 in Eqs. (64a) from (64b), one finds, with the neglect of small quantities of
in Eqs. (64a) from (64b), one finds, with the neglect of small quantities of
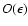 ,
that
,
that
![$\displaystyle (\bar A_{\rm m}/\bar A)\sigma_{\rm p}\tilde m(\sigma_{\rm p})=-Z ...
...~\tilde m_{\rm f}^*(\sigma_{\rm r})-\sigma_{\rm p}\tilde m^*(\sigma_{\rm r})~].$](/articles/aa/full/2003/12/aa3056/img311.gif) |
|
|
(65) |
This result enables us to compute the prograde semidiurnal nutations
from the amplitudes of the LF nutations and of the associated
wobbles of the core, since both
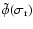 and
and
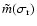 may
be expressed in terms of the amplitude of the associated nutation
with frequency
may
be expressed in terms of the amplitude of the associated nutation
with frequency
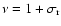 .
.
Before proceeding futher on these lines, it is useful to get an
idea of the relative magnitudes of the various terms on the right
hand side of (65). The dominant term is the first one representing
the external torque acting on the triaxiality. Both
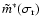 and
and
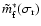 in the remaining terms are affected by the resonance at
in the remaining terms are affected by the resonance at
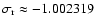 associated with the FCN. Nevertheless,
the factor
associated with the FCN. Nevertheless,
the factor
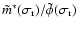 stays close to e at the frequencies of
interest here, deviating from it only by about 30% even at the
stays close to e at the frequencies of
interest here, deviating from it only by about 30% even at the 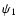 frequency (
frequency (
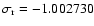 )
responsible for the
retrograde annual nutation. Therefore the contribution from the
second term on the right in (65) relative to that of the first term
is
)
responsible for the
retrograde annual nutation. Therefore the contribution from the
second term on the right in (65) relative to that of the first term
is 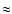
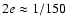 ,
since
,
since
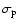 is close to unity;
hence the contribution of this term to any of the semidiurnal
polar motion coefficients is at most about 0.1
is close to unity;
hence the contribution of this term to any of the semidiurnal
polar motion coefficients is at most about 0.1 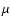 as, the
largest of the coefficients being about 15
as, the
largest of the coefficients being about 15 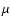 as.
If the core
is triaxial (
as.
If the core
is triaxial (
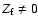 ), the huge resonance in
), the huge resonance in
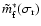 enters
the picture:
enters
the picture:
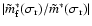 is as large as 800
for the
is as large as 800
for the 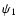 frequency, and about 200 at the frequency
(
frequency, and about 200 at the frequency
(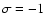 )
of the K1 tide (which causes the precession) and at
the nearby frequency with which the 18.6 year retrograde nutation
is associated. Thus, if the triaxiality of the core were to have
the same magnitude as that of the whole Earth (
)
of the K1 tide (which causes the precession) and at
the nearby frequency with which the 18.6 year retrograde nutation
is associated. Thus, if the triaxiality of the core were to have
the same magnitude as that of the whole Earth (
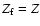 ), the
magnitude of the contribution of the
), the
magnitude of the contribution of the
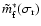 term in (65) relative to that of the external torque would become
term in (65) relative to that of the external torque would become
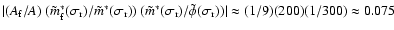 for
for
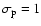 (the 0.99727 day
polar motion driven by the K1 tide); the corresponding number
is large, about 0.39, for the PM due to the
(the 0.99727 day
polar motion driven by the K1 tide); the corresponding number
is large, about 0.39, for the PM due to the 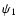 tide close to
the resonance, but only 0.0022 for that due to the O1 tide far
from the resonance. The magnitude of the actual contribution to
the larger of the PM coefficients for the 0.99727 day polar motion
turns out to be about 1
tide close to
the resonance, but only 0.0022 for that due to the O1 tide far
from the resonance. The magnitude of the actual contribution to
the larger of the PM coefficients for the 0.99727 day polar motion
turns out to be about 1 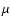 as, which is not insignificant.
Further discussion of the numerical results on the effects of core
triaxiality will be deferred to Sect. 8, where a
comparison will be made with the results of Escapa et al. (2002) who have already drawn attention to the role of the
FCN resonance in the context of semidiurnal nutations (equivalent
to the prograde diurnal polar motions).
as, which is not insignificant.
Further discussion of the numerical results on the effects of core
triaxiality will be deferred to Sect. 8, where a
comparison will be made with the results of Escapa et al. (2002) who have already drawn attention to the role of the
FCN resonance in the context of semidiurnal nutations (equivalent
to the prograde diurnal polar motions).
Returning now to the development of the theoretical
expressions, we note that no generally accepted quantitative
estimates are avaliable for the triaxiality of the
core, and so we ignore its effects hereafter. We have then, to
an approximation which neglects terms of
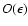 ,
,
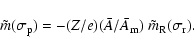 |
(66) |
In this approximation, the transfer function from the rigid to
the nonrigid Earth is simply the constant
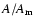 .
.
Now, in view of Eq. (62), the prograde part of the wobble in
the time domain is
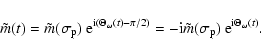 |
(67) |
The corresponding nutation is obtained using Eqs. (13), (15),
and (16) with the upper sign, remembering that m=1 and
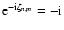 in the present case:
in the present case:
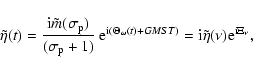 |
(68) |
where
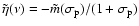 as in (17), and
as in (17), and
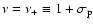 .
As for
.
As for
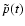 ,
one finds from (19) on using (68) that
,
one finds from (19) on using (68) that
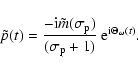 |
(69) |
If we now use the approximation (66) for
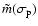 and
then replace
and
then replace
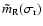 by
by
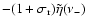 where
where
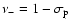 ,
and use
the expression (50) for Z, we obtain
,
and use
the expression (50) for Z, we obtain
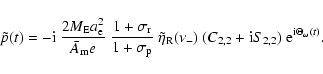 |
(70) |
This expression may be evaluated by taking the amplitudes
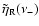 of LF nutations from the appropriate rigid Earth
nutation series. For exact results, one needs to compute the
solution for
of LF nutations from the appropriate rigid Earth
nutation series. For exact results, one needs to compute the
solution for
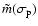 from Eqs. (64), which calls for a
knowledge of
from Eqs. (64), which calls for a
knowledge of
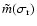 (and
(and
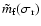 too if
too if 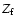 is set to a
nonzero value). These wobble amplitudes may be obtained, for
instance, by solving the standard Sasao et al. (1980)
equations. It turns out that the largest of the errors caused by
the use of (70) is at the 0.1
is set to a
nonzero value). These wobble amplitudes may be obtained, for
instance, by solving the standard Sasao et al. (1980)
equations. It turns out that the largest of the errors caused by
the use of (70) is at the 0.1 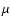 as level if triaxiality of the
core is ignored. The results shown in the tables in the next
section are the exact ones, of course.
as level if triaxiality of the
core is ignored. The results shown in the tables in the next
section are the exact ones, of course.


Up: Polar motions equivalent to mantle
Copyright ESO 2003
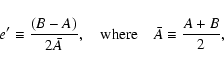
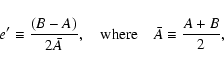
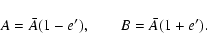
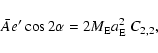
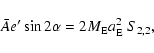
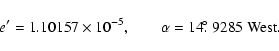
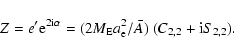
![]() ,
and
,
and ![]() in the equatorial components of the angular momentum vectors
in the equatorial components of the angular momentum vectors ![]() and
and
![]() .
In a
coordinate system with its axes along the principal axes of the
inertia tensor, the equatorial components of
.
In a
coordinate system with its axes along the principal axes of the
inertia tensor, the equatorial components of ![]() are, for the
triaxial Earth,
are, for the
triaxial Earth,
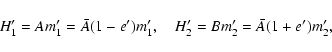
![\begin{displaymath}\tilde H'(t) = H_1'(t)+{\rm i}H_2'(t)=\bar A~[~\tilde m'(t) -e'\tilde m'^*(t)].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img245.gif)
![\begin{displaymath}\tilde H(t)= \bar A~[\tilde m(t)-Z~\tilde m^*(t)~ ].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img249.gif)
![]() asbecause of the weakness of
the driving potentials of degree >2. With the inclusion of these
terms here, the dynamical Eqs. (29) get modified to
asbecause of the weakness of
the driving potentials of degree >2. With the inclusion of these
terms here, the dynamical Eqs. (29) get modified to
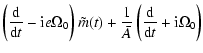
![$\displaystyle \times\left[\tilde c_3(t)+\bar A_{\rm f}\tilde m_{\rm f}(t)-\bar ...
...
Z_{\rm f}\tilde m_{\rm f}^*(t)\right] = {\tilde\Gamma(t)\over \bar A\Omega_0},$](/articles/aa/full/2003/12/aa3056/img258.gif)
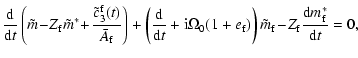
![]() .
Noting that the amplitude
of the term in
.
Noting that the amplitude
of the term in
![]() which has this time dependence is
which has this time dependence is
![]() ,
and similarly for
,
and similarly for
![]() ,
one sees that the equations
are:
,
one sees that the equations
are:
![]() ,
which is the relevant special case of (55a). On taking its complex
conjugate and making the replacement
,
which is the relevant special case of (55a). On taking its complex
conjugate and making the replacement
![]() ,
one obtains a
second equation relating
,
one obtains a
second equation relating
![]() and
and
![]() .
This pair of equations
yields the secular equation
.
This pair of equations
yields the secular equation
![]() ,
where e'=|Z|. Thus
the change in the Chandler eigenfrequency due to triaxiality is from e to
e(1-e'2/2e2), to the lowest order in the triaxiality.
Given the magnitudes of e and e', the fractional change is seen
to be of the order of 10-5, which is much too small be of
interest. For the Earth with a fluid core, a similar procedure
starting with both the Eqs. (55) and their complex conjugates
with the sign of
,
where e'=|Z|. Thus
the change in the Chandler eigenfrequency due to triaxiality is from e to
e(1-e'2/2e2), to the lowest order in the triaxiality.
Given the magnitudes of e and e', the fractional change is seen
to be of the order of 10-5, which is much too small be of
interest. For the Earth with a fluid core, a similar procedure
starting with both the Eqs. (55) and their complex conjugates
with the sign of ![]() reversed, leads to a similar result also for
the second eigenfrequency associated with the free core nutation.
reversed, leads to a similar result also for
the second eigenfrequency associated with the free core nutation.
![\begin{displaymath}\phi^{(2,1)}({\vec r};t) =
-\Omega_0^2\left[~\phi_1(t) xz+\phi_2(t) yz~\right].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img273.gif)
![\begin{displaymath}\tilde\Gamma= -{\rm i}\bar A\Omega_0^2\ \left[~e\tilde\phi(t)+Z\tilde\phi^*(t)~\right].
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img276.gif)
![]() ,
,
![]() is proportional to
is proportional to
![]() ,
,
![]() being the longitude, according to the Cartwright-Tayler
convention. This is ensured by taking the spectral components of
being the longitude, according to the Cartwright-Tayler
convention. This is ensured by taking the spectral components of ![]() and
and ![]() to be
to be 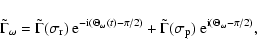
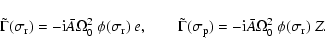
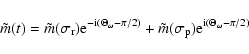
![]() and
and
![]() and introducing from Eqs. (31) the expressions
and introducing from Eqs. (31) the expressions
![]() and
and
![]() in Eqs. (64),
in Eqs. (64),
![]() is close to 1 while all other quantities except
is close to 1 while all other quantities except
![]() are
of
are
of
![]() .
Substituting for
.
Substituting for
![]() in Eqs. (64a) from (64b), one finds, with the neglect of small quantities of
in Eqs. (64a) from (64b), one finds, with the neglect of small quantities of
![]() ,
that
,
that
![]() and
and
![]() in the remaining terms are affected by the resonance at
in the remaining terms are affected by the resonance at
![]() associated with the FCN. Nevertheless,
the factor
associated with the FCN. Nevertheless,
the factor
![]() stays close to e at the frequencies of
interest here, deviating from it only by about 30% even at the
stays close to e at the frequencies of
interest here, deviating from it only by about 30% even at the ![]() frequency (
frequency (
![]() )
responsible for the
retrograde annual nutation. Therefore the contribution from the
second term on the right in (65) relative to that of the first term
is
)
responsible for the
retrograde annual nutation. Therefore the contribution from the
second term on the right in (65) relative to that of the first term
is ![]()
![]() ,
since
,
since
![]() is close to unity;
hence the contribution of this term to any of the semidiurnal
polar motion coefficients is at most about 0.1
is close to unity;
hence the contribution of this term to any of the semidiurnal
polar motion coefficients is at most about 0.1 ![]() as, the
largest of the coefficients being about 15
as, the
largest of the coefficients being about 15 ![]() as.
If the core
is triaxial (
as.
If the core
is triaxial (
![]() ), the huge resonance in
), the huge resonance in
![]() enters
the picture:
enters
the picture:
![]() is as large as 800
for the
is as large as 800
for the ![]() frequency, and about 200 at the frequency
(
frequency, and about 200 at the frequency
(![]() )
of the K1 tide (which causes the precession) and at
the nearby frequency with which the 18.6 year retrograde nutation
is associated. Thus, if the triaxiality of the core were to have
the same magnitude as that of the whole Earth (
)
of the K1 tide (which causes the precession) and at
the nearby frequency with which the 18.6 year retrograde nutation
is associated. Thus, if the triaxiality of the core were to have
the same magnitude as that of the whole Earth (
![]() ), the
magnitude of the contribution of the
), the
magnitude of the contribution of the
![]() term in (65) relative to that of the external torque would become
term in (65) relative to that of the external torque would become
![]() for
for
![]() (the 0.99727 day
polar motion driven by the K1 tide); the corresponding number
is large, about 0.39, for the PM due to the
(the 0.99727 day
polar motion driven by the K1 tide); the corresponding number
is large, about 0.39, for the PM due to the ![]() tide close to
the resonance, but only 0.0022 for that due to the O1 tide far
from the resonance. The magnitude of the actual contribution to
the larger of the PM coefficients for the 0.99727 day polar motion
turns out to be about 1
tide close to
the resonance, but only 0.0022 for that due to the O1 tide far
from the resonance. The magnitude of the actual contribution to
the larger of the PM coefficients for the 0.99727 day polar motion
turns out to be about 1 ![]() as, which is not insignificant.
Further discussion of the numerical results on the effects of core
triaxiality will be deferred to Sect. 8, where a
comparison will be made with the results of Escapa et al. (2002) who have already drawn attention to the role of the
FCN resonance in the context of semidiurnal nutations (equivalent
to the prograde diurnal polar motions).
as, which is not insignificant.
Further discussion of the numerical results on the effects of core
triaxiality will be deferred to Sect. 8, where a
comparison will be made with the results of Escapa et al. (2002) who have already drawn attention to the role of the
FCN resonance in the context of semidiurnal nutations (equivalent
to the prograde diurnal polar motions).
![]() ,
,