The formal solution of the pair of linear Eqs. (32) is
nearly trivial. Denoting the secular determinant of this system
by ![]() and the coefficient
and the coefficient
![]() of
of
![]() in the second equation by
in the second equation by ![]() ,
we have
,
we have
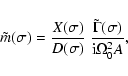 |
(33) |
| (34) |
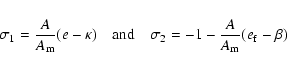 |
(35) |
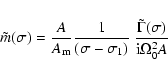 |
(36) |
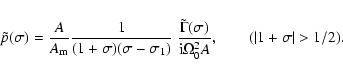 |
(37) |
If the Earth were rigid,
![]() would reduce to unity, and
would reduce to unity, and ![]() would be just e. With these substitutions, the
expression (36) reduces to the wobble amplitude
would be just e. With these substitutions, the
expression (36) reduces to the wobble amplitude
![]() of
the rigid Earth. So the transfer function from the rigid to the
nonrigid Earth becomes
of
the rigid Earth. So the transfer function from the rigid to the
nonrigid Earth becomes
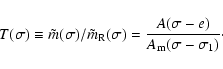 |
(38) |
When the excitation frequencies ![]() are outside the low
frequency band too, i.e., when
are outside the low
frequency band too, i.e., when
![]() (besides
(besides
![]() ),
further simplification of (36) and (38) is
possible since e and
),
further simplification of (36) and (38) is
possible since e and ![]() are then negligible relative to
are then negligible relative to ![]() which dominates by factors of the order of 300. Thus the transfer function becomes very nearly constant, equal to
which dominates by factors of the order of 300. Thus the transfer function becomes very nearly constant, equal to
![]() ;
this is the case for all nutations except
the low frequency and prograde diurnal ones.
;
this is the case for all nutations except
the low frequency and prograde diurnal ones.
Long period wobbles and polar motions (or the associated prograde diurnal nutations) have to be handled with care, because of the resonance associated with the Chandler wobble whose frequency appears in the low frequency band. These are dealt with in Sect. 6. The zero frequency term in the torque, which pertains to this band, merits special consideration, for reasons to be outlined there.
For numerical computations, which are done to an accuracy of 0.1 ![]() as and without making use of any of the approximations made
above or later, we take
as and without making use of any of the approximations made
above or later, we take
![]() ,
e=0.00328455,
and, for an elastic Earth,
,
e=0.00328455,
and, for an elastic Earth,
![]() ;
the last two are
the estimates due to Mathews et al. (2002). The other parameters
involved are
;
the last two are
the estimates due to Mathews et al. (2002). The other parameters
involved are
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
but they contribute only marginally, if at all,
to our numerical results.
,
but they contribute only marginally, if at all,
to our numerical results.
Copyright ESO 2003