Since the amplitudes of the HF nutations are expected to be no
more than about 20 ![]() as, the effects of the solid inner core
are expected to be negligible at the level of 0.1
as, the effects of the solid inner core
are expected to be negligible at the level of 0.1 ![]() as, which
is the accuracy we aim for. So we treat the Earth as consisting of
only two regions - the mantle and a fluid core.
as, which
is the accuracy we aim for. So we treat the Earth as consisting of
only two regions - the mantle and a fluid core.
The coupled rotational motions of of these two regions which are
excited by potentials of any type
![]() are governed by
dynamical equations of the Sasao et al. (1980) form for the wobble
variables
are governed by
dynamical equations of the Sasao et al. (1980) form for the wobble
variables
![]() and
and
![]() .
They are, in the time domain,
.
They are, in the time domain,
![\begin{displaymath}\left ({{\rm d}\over {\rm d}t} -{\rm i}e\Omega_0\right)\tilde...
...lde m_{\rm f}(t)\right]\!=\!{\tilde\Gamma(t)\over A\Omega_0},
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img102.gif) |
(29a) |
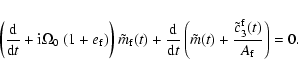 |
(29b) |
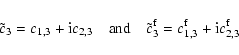 |
(30) |
The quantity
![]() in (30) represents the deformation of type (2,1) of the whole Earth due to the direct action of the tidal
potential, together with that due to incremental centrifugal
potentials associated with the wobbles
in (30) represents the deformation of type (2,1) of the whole Earth due to the direct action of the tidal
potential, together with that due to incremental centrifugal
potentials associated with the wobbles ![]() and
and
![]() .
The
origins of
.
The
origins of
![]() are similar, but the relevant deformation is
that of the core alone. For a spherically symmetric Earth, the
deformation induced by a tidal potential of type (n,m) is
strictly of the same type, and will therefore contribute nothing
to
are similar, but the relevant deformation is
that of the core alone. For a spherically symmetric Earth, the
deformation induced by a tidal potential of type (n,m) is
strictly of the same type, and will therefore contribute nothing
to
![]() or
or
![]() unless
(n,m)=(2,1). Although the
ellipticity of the Earth would result in the presence of a small
part (of the order of 1/300) of type (2,1) in the deformation due
to (n,1) potentials with
unless
(n,m)=(2,1). Although the
ellipticity of the Earth would result in the presence of a small
part (of the order of 1/300) of type (2,1) in the deformation due
to (n,1) potentials with ![]() ,
its effect on the already small nutations produced by such
potentials is entirely negligible. However, the incremental
centrifugal potentials are necessarily of type (2,1)
irrespective of the nature of the tidal potential, and so is its
contribution to deformation. Consequently, the expressions of
Sasao et al. (1980) for
,
its effect on the already small nutations produced by such
potentials is entirely negligible. However, the incremental
centrifugal potentials are necessarily of type (2,1)
irrespective of the nature of the tidal potential, and so is its
contribution to deformation. Consequently, the expressions of
Sasao et al. (1980) for
![]() and
and
![]() take the following
modified form in the general case:
take the following
modified form in the general case:
| |
= | (31a) | |
| = | (31b) |
There is a caveat to be entered in regard to the above expressions,
because the compliances have to be considered to be frequency
dependent, in general, even within a particular tidal band. The
reason is that the deformation due to ocean tides raised by the
tidal potential, and the effect of mantle anelasticity on the
deformations, are both reflected in the values of the
compliances - and one or the other of these could be strongly
frequency dependent, depending on the type (n,m)
of the potential involved (see, for instance, Mathews et al.
2002). This dependence, to the extent that it is known, can be
readily taken into account if the expressions (31) are taken in the
frequency domain, i.e., as expressions for
![]() and
and
![]() in
terms of the spectral amplitudes
in
terms of the spectral amplitudes
![]() ,
and
,
and
![]() ;
this
is what we do.
;
this
is what we do.
The frequency domain version of Eqs. (29) is now readily
obtained by replacing
![]() by
by
![]() and introducing the
expressions (31). One should keep in mind that
and introducing the
expressions (31). One should keep in mind that
![]() here stands
for
here stands
for
![]() ,
which has both prograde and retrograde parts. For any
term belonging to the prograde part,
,
which has both prograde and retrograde parts. For any
term belonging to the prograde part, ![]() is to be taken as
is to be taken as
![]() ,
and
,
and
![]() is given by (26a), while
for terms in the retrograde part,
is given by (26a), while
for terms in the retrograde part, ![]() is
is
![]() and
and
![]() is given by (26b) or (26c) according as
is given by (26b) or (26c) according as ![]() or m=0. With this understanding, we continue to use the generic
symbol
or m=0. With this understanding, we continue to use the generic
symbol ![]() in writing down the pair of frequency domain equations
for the wobbles due to a tidal perturbation of general type
in writing down the pair of frequency domain equations
for the wobbles due to a tidal perturbation of general type
![]() :
:
![\begin{displaymath}\left[(\sigma-e)+(1+\sigma)\kappa\right]~\tilde m(\sigma)+ (1...
... m_{\rm f}(\sigma)=
\tilde\Gamma(\sigma)/({\rm i}A\Omega_0^2),
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img136.gif) |
(32a) |
![\begin{displaymath}(1+\gamma)~\sigma~\tilde m(\sigma)+ \left[1+{\rm e}_{\rm f}+(1+\beta)\sigma\right]~\tilde m_{\rm f}=
0.
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img137.gif) |
(32b) |
| IERS92 | JGM3 | |||
| (k,l) | Ck,l | Sk,l | Ck,l | Sk,l |
| (2, 2) | 1.574 410 | -0.903 757 | 1.574 536 | -0.903 868 |
| (3, 1) | 2.190 181 | 0.269 185 | 2.192 799 | 0.268 012 |
| (3, 2) | 0.308 936 | -0.211 582 | 0.309 016 | -0.211 402 |
| (3, 3) | 0.100 447 | 0.197 157 | 0.100 559 | 0.197 201 |
| (4, 1) | -0.508 638 | -0.449 141 | -0.508 725 | -0.449 460 |
| (4, 2) | 0.350 670 | 0.662 571 | ||
Copyright ESO 2003