Evaluation of the torque
![]() on the Earth due to the
potential
on the Earth due to the
potential
![]() of Eq. (4) is done in Appendix A for general (n,m). Though the potential wave is strictly retrograde, the
complex combination
of Eq. (4) is done in Appendix A for general (n,m). Though the potential wave is strictly retrograde, the
complex combination
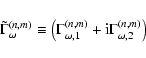 |
(23) |
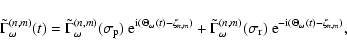 |
(24) |
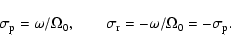 |
(25) |
It follows now from Eq. (7) that for the
torques due to nonzonal (m>0) potentials, and for the wobbles
excited by them,
![]() and
and
![]() lie in separate bands
of width 1 cpsd each, centered at m cpsd and -m cpsd,
respectively, while for m=0, the prograde and retrograde
frequencies together constitute a single band of width 1 cpsd centered at 0 cpsd. The frequency bands of the nutations
produced by
lie in separate bands
of width 1 cpsd each, centered at m cpsd and -m cpsd,
respectively, while for m=0, the prograde and retrograde
frequencies together constitute a single band of width 1 cpsd centered at 0 cpsd. The frequency bands of the nutations
produced by
![]() are shifted by +1 cpsd relative to those of
the associated wobbles, in view of (14).
are shifted by +1 cpsd relative to those of
the associated wobbles, in view of (14).
We present now explicit expressions for the amplitudes
![]() and
and
![]() (see Appendix A). The retrograde amplitude has
distinct forms for the zonal (m=0) and nonzonal cases.
(see Appendix A). The retrograde amplitude has
distinct forms for the zonal (m=0) and nonzonal cases.
| (26a) |
| (26b) |
| |
= | ||
| = | (26c) |
| Gn,m(+) | = | ||
| Gn,m | = | 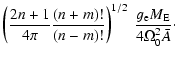 |
(27) |
In the special case of the constant term (![]() )
present in the
spectrum of any zonal potential of even order n,
)
present in the
spectrum of any zonal potential of even order n,
![]() ,
and
the expression (24) for the torque reduces to
,
and
the expression (24) for the torque reduces to
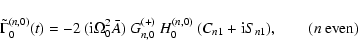 |
(28) |
It should be noted that torques due to the degree 2 sectorial (m=2) and zonal potentials are ignorable because C2,1 and S2,1 are. The origin of nutations and polar motions in the various frequency bands, as displayed in Table 1, is clear from the above considerations.
| Nutations | Frequency | due to | by potentials | Wobbles & |
| band (cpsd) | action | of type | Polar motions | |
| Long period | (-0.5,+0.5) | Cn,0 | (n,1) | Retro diurnal |
| Pro diurnal | (+0.5,+1.5) | (Cn,1,Sn,1) | (n,0) | Long period |
| Retro diurnal | (-1.5,-0.5) | (Cn,1,Sn,1) | (n,2) | Retro semidiurnal |
| Pro semidiurnal | (+1.5,+2.5) | (Cn,2,Sn,2) | (n,1) | Pro diurnal |
| Retro semidiurnal | (-2.5,-1.5) | (Cn,2,Sn,2) | (n,3) | Retro terdiurnal |
| Pro terdiurnal | (+2.5,+3.5) | (Cn,3,Sn,3) | (n,2) | Pro semidiurnal |
To compute the nutations or polar motions in a particular band of frequencies, one starts by identifying from Table 1 the types of potentials and geopotential coefficients relevant to that band, then picking out the expressions for the torques which they produce, and finally, solving the dynamical equations with these as the driving torques. For prograde semidiurnal nutations (or prograde diurnal polar motions), for instance, the relevant potentials are of type (n,1), acting on Cn,2 and Sn,2. The values of the geopotential coefficients of relevance to this work are shown in Table 2. The first set (labeled IERS92) gives the values from McCarthy (1992), used by Bretagnon et al. (1997) and other workers in computing the high frequency nutations of the rigid Earth, and the second set lists the JGM3 (Joint Gravity Model 3) values transformed to the same normalization as IERS92. We use the latter (more recent) set for our computations for the nonrigid Earth.
Copyright ESO 2003