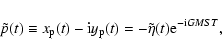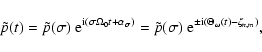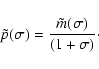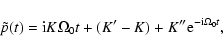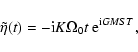Up: Polar motions equivalent to mantle
Subsections
The wobbles of the mantle and the fluid core are described by
 and
and
 ,
defined in terms of the
instantaneous angular velocity vectors
,
defined in terms of the
instantaneous angular velocity vectors
 of the
respective regions by
of the
respective regions by
![\begin{displaymath}{\vec \Omega}\!=\!\Omega_0~\left[(1+m_3)~{\vec i}_3+ {\vec m}...
...!\Omega_0~\left[m_{f3}~ {\vec i}_3+{\vec m}_{\rm f}(t)\right],
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img16.gif) |
(1) |
where
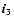 is the axis of maximum moment of inertia of
the Earth,
is the axis of maximum moment of inertia of
the Earth, 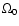 is mean angular velocity of Earth rotation,
equivalent to 1 cpsd, and m3 and
(m3+mf3) represent
the fractional variations in the axial spin rates of the
mantle and the core, respectively. As is well known, use of
the complex combinations
is mean angular velocity of Earth rotation,
equivalent to 1 cpsd, and m3 and
(m3+mf3) represent
the fractional variations in the axial spin rates of the
mantle and the core, respectively. As is well known, use of
the complex combinations
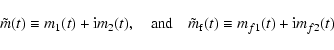 |
(2) |
of the components of
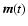 and
and
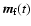 helps to express the
dynamical equations of the wobbles compactly. Their individual
spectral components have the forms
helps to express the
dynamical equations of the wobbles compactly. Their individual
spectral components have the forms
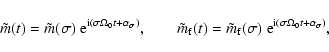 |
(3) |
where 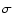 is the frequency (in cpsd) and
is the frequency (in cpsd) and
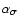 is the
phase, of the wobble;
is the
phase, of the wobble; 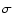 is positive (negative) for prograde
(retrograde) wobbles.
is positive (negative) for prograde
(retrograde) wobbles.
The phase of a wobble due to lunisolar forcing is related, of
course, to the argument of the relevant spectral component of the
lunisolar potential. In the convention of
Cartwright & Tayler
(1971), the potential of spherical harmonic type (n,m) and
frequency 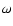 at the point with colatitude
at the point with colatitude 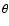 and longitude
and longitude 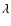 at a geocentric distance r is expressed as
at a geocentric distance r is expressed as
![\begin{displaymath}V_{\omega}^{(n,m)}({\vec r};t) = g_{\rm e} H^{(n,m)}_\omega~(...
...a,\lambda)~
{\rm e}^{{\rm i}(\Theta_\omega(t)-\zeta_{n,m})}~],
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img26.gif) |
(4) |
where 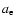 is the Earth's equatorial radius,
is the Earth's equatorial radius,
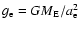 (
(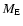 being the Earth's mass), and
being the Earth's mass), and
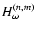 is the amplitude
(expressed as a height) and
is the amplitude
(expressed as a height) and
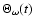 is the argument of this
spectral component of the tidal potential. The role of
is the argument of this
spectral component of the tidal potential. The role of
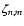 ,
defined by
,
defined by
is to ensure that the potential involves
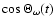 or
or
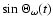 according as (n-m) is even or odd, in conformity with
the Cartwright-Tayler convention.
The argument
according as (n-m) is even or odd, in conformity with
the Cartwright-Tayler convention.
The argument
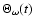 is expressed as a linear combination, with
integer coeffients, of the Doodson's fundamental tidal arguments
is expressed as a linear combination, with
integer coeffients, of the Doodson's fundamental tidal arguments
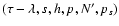 ,
with m as the coefficient of
the first of these. It is useful to note that
,
with m as the coefficient of
the first of these. It is useful to note that
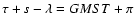 ,
GMST being the Greenwich Mean Sidereal Time (in
radians). For all practical purposes,
,
GMST being the Greenwich Mean Sidereal Time (in
radians). For all practical purposes,
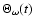 is a linear function
of time, and
is a linear function
of time, and
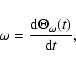 |
(6) |
with 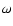 confined, for given m, to the interval
confined, for given m, to the interval
| |
|
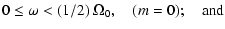 |
|
| |
|
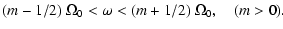 |
(7) |
The torque exerted by the potential (4) on the Earth, which is
considered in detail in the next section, has both prograde and
retrograde components. The relation between the argument
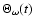 and the phases
and the phases
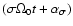 of the wobbles produced by the
respective components of the torque is
of the wobbles produced by the
respective components of the torque is
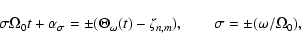 |
(8) |
wherein the upper (lower) signs are for the prograde (retrograde)
wobbles.
As we shall show in Sect. 6, an unusual situation
arises in the case of the nonrigid Earth if the driving torque is
time independent (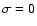 ): the solution is then not a special case
of (3), but is linear in t:
): the solution is then not a special case
of (3), but is linear in t:
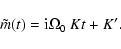 |
(9) |
The complex nutation variable
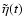 ,
defined by
,
defined by
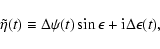 |
(10) |
is kinematically related to the mantle wobble variable
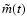 :
:
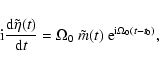 |
(11) |
where -t0 (or
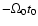 in angle units) is GMST0, the
Greenwich Mean Sidereal Time (GMST) at the epoch chosen as the
origin of time (t=0). It is conventional, in both tidal and
nutation theories, to take this epoch to be J2000, i.e.,
12 hrs UT1 on January 1, 2000, and we follow this convention.
in angle units) is GMST0, the
Greenwich Mean Sidereal Time (GMST) at the epoch chosen as the
origin of time (t=0). It is conventional, in both tidal and
nutation theories, to take this epoch to be J2000, i.e.,
12 hrs UT1 on January 1, 2000, and we follow this convention.
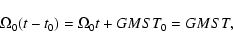 |
(12) |
where
GMST0=4.894961212 radians.
Equation (11) is a linear approximation to the exact relation, and is
entirely adequate for the present purposes. Taken together with
Eqs. (3) and (12), it implies that a wobble
of frequency 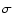 cpsd (
cpsd (
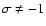 or 0) has the associated
nutation of frequency
or 0) has the associated
nutation of frequency  cpsd:
cpsd:
where, in view of the second of Eqs. (8),
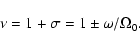 |
(14) |
The plus (minus) sign in the above equation is for prograde
(retrograde) wobbles.
Now, the conventional argument 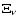 of a nutation of frequency
of a nutation of frequency
 is related to the argument
is related to the argument
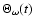 of the tide which excites
the nutation through
of the tide which excites
the nutation through
| |
|
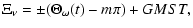 |
(15a) |
| |
|
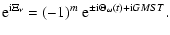 |
(15b) |
Therefore the expression (13) for
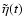 becomes, for a nutation
excited by a tidal potential of order m,
becomes, for a nutation
excited by a tidal potential of order m,
The relations (15) give rise to the factor (-1)m
which appears in (16). This factor which would have been missed if
the constants in the phases of the wobbles and nutations were not
explicitly kept track of, and the factor e
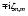 (which is 1 or
(which is 1 or 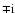 according as n-m is even or odd), play essential
roles in correctly identifying the coefficients of
according as n-m is even or odd), play essential
roles in correctly identifying the coefficients of
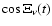 and
and
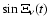 computed from the tidal potential, and in ensuring
that they have the correct signs.
computed from the tidal potential, and in ensuring
that they have the correct signs.
The special case
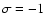 leads to a secularly varying
leads to a secularly varying
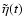 ,
representing precession:
,
representing precession:
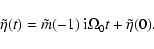 |
(18) |
Polar motion is represented by
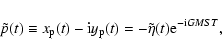 |
(19) |
as has been made explicit by Gross (1992) and
Brzezinski & Capitaine (1993).
It is evident that its frequency is
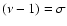 cpsd, i.e.,
the same as that of the associated wobble. One obtains, on
using (13),
cpsd, i.e.,
the same as that of the associated wobble. One obtains, on
using (13),
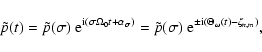 |
(20) |
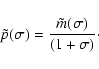 |
(21) |
In the special case when the torque is time independent (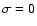 ),
one finds on integrating Eq. (11) with
),
one finds on integrating Eq. (11) with
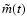 taken from (9),
and then using (19), that
taken from (9),
and then using (19), that
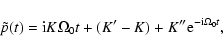 |
(22a) |
where K' and K'' involve the intial values of 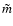 and
and 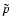 .
The specifics of this case are dealt with in
Sect. 6. The nutation corresponding to (22a) is
.
The specifics of this case are dealt with in
Sect. 6. The nutation corresponding to (22a) is
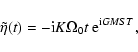 |
(22b) |
with the omission of the initial value terms. A nutation of this
type, which is periodic but with an amplitude varying linearly with
time, appears to have been not encountered before.


Up: Polar motions equivalent to mantle
Copyright ESO 2003
![]() and
and
![]() ,
defined in terms of the
instantaneous angular velocity vectors
,
defined in terms of the
instantaneous angular velocity vectors
![]() of the
respective regions by
of the
respective regions by
![\begin{displaymath}{\vec \Omega}\!=\!\Omega_0~\left[(1+m_3)~{\vec i}_3+ {\vec m}...
...!\Omega_0~\left[m_{f3}~ {\vec i}_3+{\vec m}_{\rm f}(t)\right],
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img16.gif)
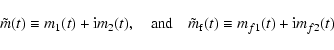
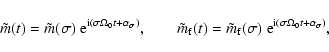
![]() at the point with colatitude
at the point with colatitude ![]() and longitude
and longitude ![]() at a geocentric distance r is expressed as
at a geocentric distance r is expressed as
![\begin{displaymath}V_{\omega}^{(n,m)}({\vec r};t) = g_{\rm e} H^{(n,m)}_\omega~(...
...a,\lambda)~
{\rm e}^{{\rm i}(\Theta_\omega(t)-\zeta_{n,m})}~],
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img26.gif)
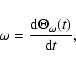
![]() ,
defined by
,
defined by
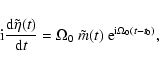
![]() cpsd (
cpsd (
![]() or 0) has the associated
nutation of frequency
or 0) has the associated
nutation of frequency ![]() cpsd:
cpsd:
![]() of a nutation of frequency
of a nutation of frequency
![]() is related to the argument
is related to the argument
![]() of the tide which excites
the nutation through
of the tide which excites
the nutation through
![]() leads to a secularly varying
leads to a secularly varying
![]() ,
representing precession:
,
representing precession: