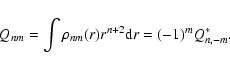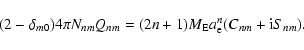Up: Polar motions equivalent to mantle
We start with the expression (4), written slightly more explicitly:
The surface spherical harmonics Ynm, (
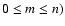 ,
are
defined here by
,
are
defined here by
The torque on the Earth due to the potential
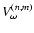 is
is
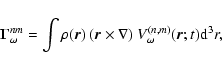 |
(A.3) |
where
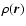 is the density at the postion
is the density at the postion 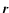 ,
and
the integral is over the volume of the Earth. The operator
,
and
the integral is over the volume of the Earth. The operator
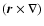 is proportional to the angular momentum
operator
is proportional to the angular momentum
operator 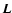 of quantum mechanics. Knowing the
action of
of quantum mechanics. Knowing the
action of 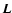 on Ynm (see, for instance,
Mathews & Venkatesan 1976),
one finds immediately that
on Ynm (see, for instance,
Mathews & Venkatesan 1976),
one finds immediately that
where
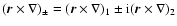 and
and
|
cnm = [ (n-m)(n+m+1) ]1/2.
|
(A.5) |
We can now carry out the angular part of the integration in (A3)
with the help of a spherical harmonic expansion of
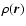 :
:
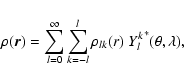 |
(A.6) |
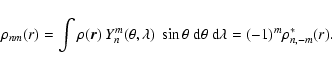 |
(A.7) |
On introducing (A6) together with (A1) into (A3) and making use
of
Eqs. (A2) and (A4), we obtain the following expressions for
the familiar complex combination
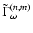 of the first two
components of
of the first two
components of
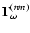 :
:
![$\displaystyle \tilde\Gamma^{(n,m)}_\omega= {\rm i}{g_{\rm e}\over 2a_{\rm e}^n}...
...
-c_n^{-m}~
{Q_{n,m-1}}^*~{\rm e}^{{\rm -i}(\Theta_\omega(t)-\zeta_{n,m})}\Big]$](/articles/aa/full/2003/12/aa3056/img421.gif) |
|
|
(A.8) |
for m> 0, and
![\begin{displaymath}\tilde\Gamma^{(n0)}_\omega={\rm i}{g_{\rm e}\over 2a_{\rm e}^...
...})}+
~{\rm e}^{{\rm -i}(\Theta_\omega(t)-\zeta_{n,0})}~\right]
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img422.gif) |
(A.9) |
for m=0, where
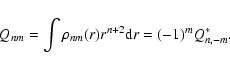 |
(A.10) |
The Qnm are related, of course, to the geopotential
coefficients
(Cnm,Snm). The relation is
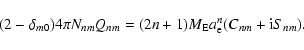 |
(A.11) |
The expressions given in Eqs. (26) of the text are obtained
on substituting for Qnm in (A8) and (A9) from (A11). The
entries in Table 1 regarding the origins of the wobbles and
nutations in various frequency bands are based on Eqs. (A8) and (A9). The prograde/retrograde nature of the two terms
in each of these equations is evident from the fact that
the contribution to
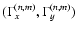 from
the first term is proportional to
from
the first term is proportional to
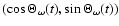 which rotates in the prograde sense, while the contribution from
the second term, proportional to
which rotates in the prograde sense, while the contribution from
the second term, proportional to
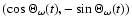 ,
is
retrograde.
,
is
retrograde.


Up: Polar motions equivalent to mantle
Copyright ESO 2003
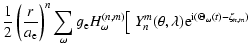
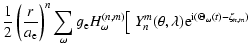
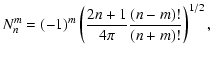
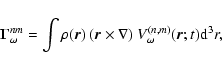
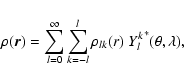
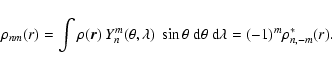
![\begin{displaymath}\tilde\Gamma^{(n0)}_\omega={\rm i}{g_{\rm e}\over 2a_{\rm e}^...
...})}+
~{\rm e}^{{\rm -i}(\Theta_\omega(t)-\zeta_{n,0})}~\right]
\end{displaymath}](/articles/aa/full/2003/12/aa3056/img422.gif)