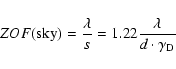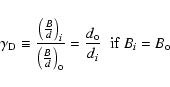Up: Imaging capabilities of hypertelescopes
The principle of densified-pupil multi-aperture imaging
interferometers, called hypertelescopes, was previously described
(Labeyrie 1996; Gillet et al. 2001; Riaud et al. 2002).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3943f1.eps}\end{figure}](/articles/aa/full/2003/10/aah3943/Timg8.gif) |
Figure 1:
Hypertelescope principle.
Positive (left) and negative (right) pupil densification, using
respectively a diverging and a converging lens array, followed in each case
by a longer-focus array of converging lenses. A tilted incoming
wavefront from an off-axis star is densified
with two confocal lens arrays (ML1 and ML2), thus producing a densified
wavefront which focuses to a single narrow interference peak within the broader diffraction pattern from each sub-pupil.
It becomes stair-shaped since the slope of each wavefront
segment is reduced by the pair of micro-lenses. The stair's
average shape remains flat and parallel to the incoming
wavefront since all pairs of micro-lenses introduce identical
propagation delays. But each wavefront segment, arriving with a slope
angle 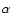 ,
emerges with an angle ,
emerges with an angle
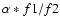 where f1and f2 are the micro-lens's focal lengths of ML1 and ML2. The
resulting wavefront is finally a stair-shaped wavefront with the same
average slope as at the entrance of the densifier.
where f1and f2 are the micro-lens's focal lengths of ML1 and ML2. The
resulting wavefront is finally a stair-shaped wavefront with the same
average slope as at the entrance of the densifier. |
Let us consider light beams coming from N small mirrors arrayed
periodically in two dimensions with period s. Beams from these
mirrors are initially combined according to a Fizeau
interferometer geometry. At the combined focus, the image has a
central peak surrounded by many secondary dispersed peaks.
Densifying the entrance pupil, shrinks and intensifies the
combined image, thus attenuating or suppressing the secondary
peaks. The densified pupil increases the limiting magnitude but
limits the field of view to a non-aliased field of the interferometer.
The white central peak, in the densified-pupil image, appears only
for stars within a small region of the sky. Following
Gillet et al. (2001), we call ZOF (Zero Order Field) this narrow usable
field and HOF (High Order Field) the peripheral sky field of size
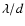 where d is the size of one sub-aperture (1 mm):
where d is the size of one sub-aperture (1 mm):
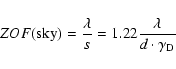 |
(1) |
where
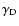 the densification ratio. This
densification ratio is defined by:
the densification ratio. This
densification ratio is defined by:
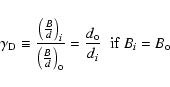 |
(2) |
where di and 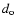 are the entrance mirror and exit
sub-pupil diameters respectively, and Bi and
are the entrance mirror and exit
sub-pupil diameters respectively, and Bi and 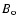 the entrance
and exit baselines in the pupil densifier. In the
configuration considered here (Fizeau interferometer), both
baselines are equal. But in case of a Michelson interferometer,
the entrance baseline Bi is different from the output baseline
the entrance
and exit baselines in the pupil densifier. In the
configuration considered here (Fizeau interferometer), both
baselines are equal. But in case of a Michelson interferometer,
the entrance baseline Bi is different from the output baseline 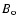 .
.
The number of resolution elements in the ZOF is given by:
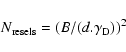 |
(3) |
B is the baseline of the interferometer (here 10 cm).


Up: Imaging capabilities of hypertelescopes
Copyright ESO 2003
![]() where d is the size of one sub-aperture (1 mm):
where d is the size of one sub-aperture (1 mm):