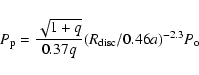Up: Double-periodic blue variables in
The long-term well behaved sinusoidal modulations observed in
our sample is not known to occur in other types of
blue variable stars. Here we propose as a
possible cause for the long-term oscillation the precession of an
elliptical disc around a blue star in a semi-detached binary system.
The origin of the disc ellipticity and precession
could be the tidal interaction between the disc and
the Roche-lobe filling secondary star,
in a similar way that occurs in short-orbital period dwarf novae
of the SU UMa class during superoutburst (e.g. Patterson 2001).
Table 1:
The double-periodic blue stars. OGLE name and MACHO identification are given
for every star, along with their photometric period and error.
The half amplitude of the long-term
variation is also given for the OGLE I band and the MACHO b band, along with the
epoch (HJD-2 400 000) for the faint-to-bright mean level crossing for the
MACHO b band. The half amplitude of the MACHO b-r light curve
is also given, along with their difference in phase with the b curve, considering
the epoch for positive to negative mean b-r level crossing as reference.
Dashes indicate non-detected or marginal colour variations. A note indicates the
appearance of the short-term variability: double-wave (dw),
single wave (sw) or eclipsing (e).
|
Star |
MACHO ID |
P1 (d) |
P2 (d) |
AI |
Ab |
Eb |
Ab-r |
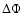 |
Note |
|
OGLE00451755-7323436 |
212.15675.158 |
5.178(5) |
171(15) |
0.12 |
0.11 |
50350.2(8) |
0.02 |
-0.35 |
dw |
| OGLE00474820-7319061 |
212.15847.466 |
5.497(7) |
177(10) |
0.12 |
0.10 |
50329.3(7) |
- |
- |
dw |
| OGLE00553643-7313019 |
211.16304.169 |
5.092(5) |
176(17) |
0.08 |
0.04 |
50238(1) |
0.02 |
0.53 |
dw |
| OGLE05025323-6909493 |
1.3686.53 |
8.025(18) |
255(30) |
0.17 |
- |
- |
- |
- |
dw |
| OGLE05040378-6917508 |
1.3805.130 |
6.223(7) |
207(20) |
0.11 |
- |
- |
- |
- |
dw |
| OGLE05060009-6855025 |
1.4174.42 |
3.849(7) |
230(22) |
0.19 |
- |
- |
- |
- |
sw |
| OGLE05101621-6854290 |
79.4900.185 |
4.301(6) |
319(34) |
0.06 |
0.04 |
50344(2) |
0.02 |
0.53 |
sw |
| OGLE05115466-6846369 |
2.5144.4555 |
9.138(2) |
361(29) |
0.26 |
- |
- |
- |
- |
e |
| OGLE05142677-6910559 |
79.5501.400 |
6.515(2) |
224(14) |
0.13 |
0.08 |
50430(2) |
0.04 |
-0.43 |
e |
| OGLE05143758-6852259 |
79.5506.139 |
5.372(6) |
185(11) |
0.14 |
0.10 |
50237.3(5) |
0.03 |
0.55 |
dw? |
| OGLE05152654-6923257 |
79.5740.5092 |
6.292(8) |
205(15) |
0.04 |
0.04 |
50275.3(6) |
- |
- |
dw |
| OGLE05155332-6925581 |
79.5739.5807 |
7.2835(16) |
188(11) |
0.11 |
0.08 |
50254(1) |
0.03 |
0.54 |
e |
| OGLE05171401-6936374 |
78.5979.58 |
8.309(4) |
311(21) |
0.13 |
0.08 |
50345(1) |
0.03 |
0.48 |
e |
| OGLE05194110-6931171 |
78.6343.81 |
6.9044(10) |
226(13) |
0.11 |
0.06 |
50247(2) |
0.02 |
0.59 |
e |
| OGLE05195898-6917013 |
80.6468.83 |
2.410(10) |
140(5) |
0.06 |
0.04 |
50267.6(8) |
- |
- |
sw |
| OGLE05203325-6910146 |
80.6469.95 |
5.737(5) |
182(10) |
0.04 |
0.05 |
50357.1(8) |
- |
- |
dw |
| OGLE05260516-6954534 |
77.7426.140 |
3.632(3) |
233(15) |
0.07 |
0.07 |
50425.7(7) |
- |
- |
sw |
| OGLE05274332-6950556 |
77.7669.1013 |
7.320(11) |
227(20) |
0.05 |
0.03 |
50280(1) |
0.02 |
0.54 |
dw |
| OGLE05285370-6952194 |
77.7911.26 |
15.854(31) |
620(70) |
0.07 |
0.06 |
50388(2) |
0.01 |
0.67 |
dw |
| OGLE05294913-6949103 |
77.8033.140 |
7.184(8) |
258(20) |
0.10 |
0.09 |
50382.2(6) |
0.01 |
-0.38 |
dw |
| OGLE05295881-6934075 |
77.8036.5142 |
5.597(4) |
179(8) |
0.12 |
- |
- |
- |
- |
dw |
| OGLE05313130-7012584 |
7.8269.36 |
9.231(21) |
960(176) |
0.04 |
0.03 |
51226(4) |
- |
- |
sw |
| OGLE05333926-6956229 |
81.8636.51 |
7.863(15) |
257(18) |
0.03 |
0.01 |
50335(2) |
0.01 |
0.52 |
dw |
| OGLE05371342-7010580 |
11.9237.2121 |
10.913(23) |
421(40) |
0.12 |
- |
- |
- |
- |
dw |
| OGLE05390681-7027487 |
11.9475.96 |
6.967(12) |
276(15) |
0.10 |
0.01 |
50335(2) |
0.01 |
0.52 |
dw |
| OGLE05390992-7019262 |
11.9477.138 |
6.632(8) |
198(15) |
0.10 |
0.05 |
50301(1) |
0.02 |
0.56 |
dw |
| OGLE05391746-7044019 |
11.9592.22 |
7.151(8) |
219(20) |
0.06 |
0.04 |
50401.0(8) |
0.01 |
-0.49 |
dw |
| OGLE05410217-7011043 |
76.9842.2444 |
7.352(13) |
264(26) |
0.11 |
0.11 |
50395(2) |
- |
- |
dw |
| OGLE05410942-7002215 |
76.9844.110 |
6.586(9) |
245(23) |
0.12 |
0.09 |
50510(2) |
- |
- |
dw |
| OGLE05435003-7057431 |
15.10314.144 |
5.012(5) |
173(12) |
0.12 |
0.09 |
50250.7(7) |
- |
- |
dw |
The 3:1 resonance between a disc particle orbiting the primary and
the binary system occurs at
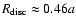 ,
where a is the binary separation. Elliptical orbits at this radius will experience a
dynamical apsidal advance with a period given by:
,
where a is the binary separation. Elliptical orbits at this radius will experience a
dynamical apsidal advance with a period given by:
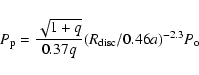 |
(3) |
(Murray 2000) where q is the ratio between the mass of the
secondary star and the primary star and 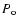 the orbital period.
If we interpret P1 as the orbital period and P2 as the precession period, then the above equation
imposes a strong correlation between both periodicities,
as effectively seen in Fig. 3.
The observed slope of
the orbital period.
If we interpret P1 as the orbital period and P2 as the precession period, then the above equation
imposes a strong correlation between both periodicities,
as effectively seen in Fig. 3.
The observed slope of
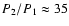 should imply a mass ratio
should imply a mass ratio
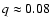 for
for
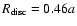 .
There are few Algols
with q < 0.1 (e.g. Richards & Albright 1999), and they do not show
the long-term oscillations described in this paper. However it is
exciting that only in these low q systems two important conditions
are fulfilled:
the primary radius is smaller than the stream circularization radius,
making possible the formation of
an accretion disc (e.g. Richards & Albright 1999) and the 3:1 resonance radius
is below the tidal truncation radius, so the disc could in principle
grown beyond the 3:1 resonance and may eventually start to precess (Fig. 4).
The secondary eclipse, in this view, could be the eclipse of the
disc.
.
There are few Algols
with q < 0.1 (e.g. Richards & Albright 1999), and they do not show
the long-term oscillations described in this paper. However it is
exciting that only in these low q systems two important conditions
are fulfilled:
the primary radius is smaller than the stream circularization radius,
making possible the formation of
an accretion disc (e.g. Richards & Albright 1999) and the 3:1 resonance radius
is below the tidal truncation radius, so the disc could in principle
grown beyond the 3:1 resonance and may eventually start to precess (Fig. 4).
The secondary eclipse, in this view, could be the eclipse of the
disc.
We have examined an alternative explanation suggested by the referee, namely,
nodal precession of a tilted disc. However,
this phenomenon seems to appear in X-ray binaries with very different
mass ratios (and different
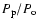 values, e.g. Larwood 1998) and not to be confined to the low mass ratio region, as suggested by the
strong concentration of
values, e.g. Larwood 1998) and not to be confined to the low mass ratio region, as suggested by the
strong concentration of
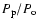 values around 35.
values around 35.
Acknowledgements
We thank the referee J. Thorstensen, and also D. Sasselov,
for interesting comments on a
first version of this paper.
REM acknowledges support by Grant Fondecyt 1030707 and
DI UdeC 202.011.030-1.0. MPD thanks CNPq support under grant
# 301029.
This paper utilizes public domain data originally obtained by the OGLE and
MACHO Projects.


Up: Double-periodic blue variables in
Copyright ESO 2003