A&A 399, 197-210 (2003)
DOI: 10.1051/0004-6361:20021773
D. Wiebe1 - D. Semenov2 - Th. Henning3
1 - Institute of Astronomy of the RAS,
Pyatnitskaya St. 48, 119017 Moscow, Russia
2 -
Astrophysical Institute and University
Observatory,
Schillergäßchen 2-3, 07745 Jena, Germany
3 -
Max Planck Institute for Astronomy,
Königstuhl 17, 69117 Heidelberg, Germany
Received 20 September 2002 / Accepted 27 November 2002
Abstract
We present a new method to analyse and reduce chemical
networks and apply this technique to the chemistry in molecular clouds.
Using the technique, we investigated the possibility of reducing the number
of chemical reactions and species in the UMIST 95 database
simultaneously. In addition, we did the same reduction but with the
"objective technique'' in order to compare both methods. We found that
it is possible to compute the abundance of carbon monoxide and fractional
ionisation accurately with significantly reduced chemical networks in the
case of pure gas-phase chemistry. For gas-grain chemistry involving surface
reactions reduction is not worthwhile. Compared to the "objective
technique'' our reduction method is more effective but more time-consuming
as well.
Key words: astrochemistry - stars: formation - molecular processes - ISM: molecules - ISM: abundances
Despite the significant growth of computer power over the last years, the modelling of the chemical evolution of protostellar cores and protoplanetary discs is still a challenging computational task. This is even more true if one aims at the simultaneous self-consistent modelling of the dynamical and chemical evolution of these systems.
The mathematical formulation of the chemical processes in space is realised by differential equations describing chemical kinetics. They contain terms for all chemical reactions expected to proceed efficiently in the interstellar medium (ISM). Along with abundances of all involved species, these terms depend on the rate coefficients that are summarised in special databases. The relevant astrochemical rate files, like the UMIST rate file or Ohio New Standard Model, comprise hundreds of species and thousands of reactions (Millar et al. 1991,1997; Le Teuff et al. 2000; Terzieva & Herbst 1998; Aikawa & Herbst 1999). Of course, one can only wonder if these databases contain all the information about reactions needed to accurately reproduce observed abundances of interstellar molecules. The opposite question to ask is if all this information is always needed.
In many astronomically interesting situations it is enough to follow the evolution of a limited number of species only. Intuitively, it seems to be apparent that to predict an abundance of N2H+, for example, one can afford computing C10abundance with less accuracy or even ignore this molecule altogether. In most cases, though, modelling of the chemical evolution of a parcel of the interstellar gas under fixed conditions or in a limited predefined range of conditions is not very time-consuming, so one probably will not be eager to sacrifice any accuracy even for the sake of order of magnitude gain in computational speed. However, in the case of dynamical modelling with changing density, UV intensity, temperature etc., a reduced chemical network may help to distinguish between feasible and non-feasible problems or at least to ease the computational burden if parallel processors are in use. One possible application for reduced chemical networks would be the modelling of the evolution of magnetised protostellar clouds or protoplanetary accretion discs, when it is necessary to compute the fractional ionisation self-consistently. Another example of dynamically important species is carbon monoxide (CO) which under certain conditions can be the most important molecular coolant (see, for example, Glassgold & Langer 1973).
Several authors have already used reduced chemical networks, based on the above arguments, however, without presenting accurate mathematical considerations (e.g., Gerola & Glassgold 1978; Howe et al. 1994; El-Nawawy et al. 1997). Recently, Ruffle et al. (2002) (hereafter RRPHH) and Rae et al. (2002) (hereafter RBHPR) made a first attempt to reduce astrochemical networks by so-called "objective reduction techniques'', developed in combustion chemistry. They have shown that it is possible to quantify the reduction task by introducing a certain criterion that would allow in each particular case to indicate, abundances of which species must be followed in order to have a reasonable estimate for an abundance of a species under investigation. For static regions with physical conditions typical of diffuse clouds, they isolated the species set that contains tens instead of hundreds species. This reduction only introduces a factor of two uncertainty in predicted CO abundance. The same task has been solved for the fractional ionisation as well.
We perform a similar analysis of the UMIST 95 chemical reaction database in order to find if it is possible to reduce the number of species and/or reactions in the chemical networks used to calculate ionisation degree and carbon monoxide abundance under conditions typical of molecular clouds. Unlike RRPHH and RBHPR, we partly focus on the medium that is more advanced toward the formation of a star. This situation is more complicated from the chemical point of view. First, pre-stellar clouds are often shielded from the interstellar UV radiation field. Dissociating photons, being an additional chemical factor, in effect simplify the chemical network, as they prevent many complex species from being formed. Reactions on grain surfaces are another factor that cannot be ignored in dense clouds.
The paper is organised as follows. First, we describe our chemical model in Sect. 2. The species-based and reaction-based reduction methods are outlined in Sect. 3. Results of reductions obtained with both methods are presented in Sect. 4 (ionisation degree) and Sect. 5 (CO). These results are discussed in Sect. 6. A conclusion follows.
We take the rates for gas-phase reactions from the UMIST 95 rate file (Millar et al. 1997). In addition to gas-phase chemistry, gas-dust interaction and dust surface reactions are considered in some of the models. The rates at which surface reactions proceed and the very applicability of the rate approximation to surface chemistry still remain a subject of debate. This is why many authors prefer to neglect surface reactions altogether (for instance, see Aikawa & Herbst 1999; Bergin & Langer 1997; Bergin et al. 1995; Charnley et al. 2001). However, in the attempt to constrain the chemical network in a cold and dense molecular cloud core, taking into account gas-dust interactions seems to be unavoidable, as dust is now widely believed to play a crucial role in molecular cloud chemistry, serving both as a sink for frozen-out species and as a catalyst for the synthesis of complex molecules (see, however, Turner 2000). In this paper we seek not to reproduce any particular abundance pattern observed in molecular clouds, but rather to investigate the very possibility of reduction when surface reactions are present. This is why we did not try to incorporate any new ideas about surface chemistry.
We solve equations of chemical kinetics for the range of fixed physical
conditions, listed in Table 1, where model designations are
given as well. Gas and dust temperatures are 10 K in all cases. No direct
UV radiation is present, implying the conditions, typical of obscured
regions, like cores of molecular clouds, where the visual extinction
![]() mag. Dust grains are assumed to be silicate-like
spheres with a constant size
mag. Dust grains are assumed to be silicate-like
spheres with a constant size
![]()
![]() ,
density
,
density
![]() g cm-3, and 106 surface sites for adsorption
(Hasegawa et al. 1992). Dust is supposed to constitute
g cm-3, and 106 surface sites for adsorption
(Hasegawa et al. 1992). Dust is supposed to constitute ![]() of
the gas density by mass.
of
the gas density by mass.
All abundances in the paper are given with respect to the number of hydrogen nuclei. We use "high metal'' and "low metal'' sets of initial abundances (e.g. Lee et al. 1998) quoted in Table 2. In the "high metal'' set the standard solar elemental composition is corrected with a modest depletion of 2 for S and stronger depletions of 10 for Na, 50 for Si, 60 for Mg, and 110 for Fe. The "low metal'' values contain additional depletion factors of 100 for each of these elements. The abundances of all elements but P and Cl are taken from Aikawa et al. (1996). For P and Cl we take values from Grevesse & Sauval (1998) and use the same depletion factors as for Fe. Hydrogen is assumed to be completely in molecular form initially. All other elements are present in atomic form at t=0.
Below details of the adopted model of gas-dust interaction are provided.
| Notation | Meaning |
| DIFF |
|
| DENS |
|
| GAS | Gas-phase network (
|
| GAD | GAS with accretion and desorption |
| (
|
|
| DUST | GAD with surface reactions (
|
| HM | "High metals'' |
| LM | "Low metals'' |
| Element | "High metals'' | "Low metals'' |
| He | 9.75(-2) | 9.75(-2) |
| C | 7.86(-5) | 7.86(-5) |
| N | 2.47(-5) | 2.47(-5) |
| O | 1.80(-4) | 1.80(-4) |
| S | 9.14(-6) | 9.14(-8) |
| Si | 9.74(-7) | 9.74(-9) |
| Na | 2.25(-7) | 2.25(-9) |
| Mg | 1.09(-6) | 1.09(-8) |
| Fe | 2.74(-7) | 2.74(-9) |
| P | 2.16(-8) | 2.16(-10) |
| Cl | 1.00(-7) | 1.00(-9) |
The accretion rate
![]() of the ith species is given by
of the ith species is given by
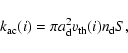
Following Umebayashi & Nakano (1980), we suppose that all grains
have unit negative charge and thus can act as electron donors in the
same reactions of dissociative recombination that occur in the gas
phase. The rate coefficient for reactions of dissociative recombination
on grain surfaces is given by
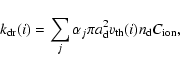 |
(1) |
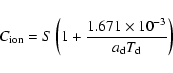 |
(2) |
The two desorption processes taken into account in our model are thermal evaporation and cosmic ray induced desorption.
The thermal evaporation rate
![]() of the ith surface species is
of the ith surface species is
| (3) |
The cosmic ray desorption rate
![]() of the ith surface
species can be estimated as
of the ith surface
species can be estimated as
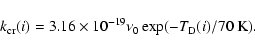 |
(4) |
| (5) |
The surface reactions as well as their rates are taken from Hasegawa et al. (1992) with the appropriate correction for different densities. Activation energy of 1000 K is adopted for O + CO surface reaction (Hasegawa & Herbst 1993).
Three chemical networks are considered. The first one is the pure gas-phase network GAS. It consists of electrons, 12 atoms, 137 molecules, and 245 ions (395 species in total) involved in 3864 gas-phase reactions. The gas-grain network GAD is supplemented by 148 surface species and 729 gas-grain interaction processes (accretion, desorption, and surface ion recombination). The gas-grain network DUST contains 192 additional surface reactions. These networks form the basis of our investigations. In the rest of the text we refer to them as "full'' networks. Equations of chemical kinetics are solved with the standard DVODE solver. Adopted solver parameters are given in the appendix.
To reduce the number of species and/or reactions in a chemical network, one has to provide a mathematical method designed to estimate the significance of particular species or reactions to the evolution of the species under consideration. In this paper we elaborate two such methods that are outlined in this section.
This technique is derived from the method used by RRPHH and RBHPR. They have shown that it is possible to reduce the number of species in a chemical network in order to compute abundances of selected species with a reasonable accuracy. The species-based reduction technique is based on the strategy to specify important species and then to select from the entire set only necessary species, that must be included in the chemical network in order to compute abundances of important species with a reasonable accuracy.
Initially, the reduced species set consists of N0 important species
only. For each species in the entire set we compute the value
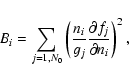 |
(6) |
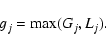 |
(8) |
| (9) |
It should be kept in mind that this method represents only the first part of the algorithm proposed by RRPHH.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ms3106f1.eps}\end{figure}](/articles/aa/full/2003/07/aa3106/Timg38.gif) |
Figure 1:
Representative B values for the HM-GAS-DIFF model
computed at t=107 years. Important species
are Mg+ and S+. The value of the cut-off
parameter
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{ms3106f2.eps}\end{figure}](/articles/aa/full/2003/07/aa3106/Timg39.gif) |
Figure 2:
Representative |
| Open with DEXTER | |
This new method allows to select only those species and reactions from the entire network that are necessary to compute abundances of important species with a reasonable accuracy. Unlike the species-based reduction technique, where the number of reactions is decreased only as a by-product of the lower number of species, in this method the numbers of unnecessary species and ineffective reactions are reduced simultaneously. In addition to the significantly shortened computational time, this could be useful if one aims at key destruction and formation pathways for important species, where a smaller number of chemical reactions makes the analysis easier.
The basic idea of the reaction-based reduction is to search for the production and destruction reactions, most important for the evolution of an important species, and to determine their relative significance. This is done via the analysis how sensitive the net formation (or loss) rate of a given species is to the presence of particular reactions at a certain physical time.
At the beginning, the chemical model is computed with the full network in order to obtain abundances of all species from the network during the entire evolutionary time span.
Second, the important species are specified. Further, the algorithm
estimates the weights of all species ![]() and reactions
and reactions ![]() in order to quantify their importance for the evolution of the species under
investigation by the following iterative process.
in order to quantify their importance for the evolution of the species under
investigation by the following iterative process.
At the first iteration, weights of important species are set to 1 and weights
of all other species are set to 0. At the ith iteration all possible formation
and destruction pathways of the current species si are found and their
significance values
![]() are specified as
are specified as
Consequently, a new set of species, which are found at that
iteration to be necessary for the evolution of the important
species and which were not considered at previous iterations, is
formed. Their weights ![]() are estimated as the maximum possible
values of the weights
are estimated as the maximum possible
values of the weights ![]() of the reactions they are involved
in. Then these species are added to the set of necessary species,
and the last two steps are repeated. This process is performed for several
stages during the computational time.
of the reactions they are involved
in. Then these species are added to the set of necessary species,
and the last two steps are repeated. This process is performed for several
stages during the computational time.
The iterations are stopped when all species and all time moments are
considered. Then one obtains a reduced chemical network from the
full network by choosing only those reactions, that have weights ![]() exceeding a pre-defined cut-off threshold
exceeding a pre-defined cut-off threshold
![]()
| (12) |
We use the two reduction techniques described in the previous section to build the reduced chemical networks that could be used for the computation of the ionisation degree in molecular clouds. All the models are first computed with the full chemical networks. Then we apply the reduction techniques and compare the ionisation degree computed with the full and reduced networks. The results of the reduction together with relevant computational speed gains are summarised in Tables 3-5.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{ms3106f3.eps}\end{figure}](/articles/aa/full/2003/07/aa3106/Timg46.gif) |
Figure 3: Ionisation degree (top and middle panels) and relative errors (bottom panel) in a diffuse cloud, computed with the full and reduced networks for pure gas-phase chemistry (HM-GAS-DIFF and LM-GAS-DIFF models). Top panel reproduces results of the reaction-based reduction. Indicated are the "exact'' solutions for high (dotted line) and low (solid line) metallicities as well as the solution for the reduced species sets (HM - dashed line, LM - long-dashed line). Middle and bottom panels illustrate the results of the species-based reduction. Shown are the "exact'' solutions (HM - dashed line, LM - solid line) and the solutions for various reduced sets (see text). |
| Open with DEXTER | |
| Model | Important | Reduced | Speed |
| species | network | gain | |
| Species-based reduction | |||
| HM-GAS-DIFF | S+ |
|
|
| HM-GAS-DIFF | S+, Mg+ |
|
|
| LM-GAS-DIFF | H+3 |
|
|
| LM-GAS-DIFF | H+3, HCO+ |
|
|
| Reaction-based reduction | |||
| HM-GAS-DIFF | e- |
|
550 |
| LM-GAS-DIFF | e- |
|
490 |
| HM-DUST-DIFF | e- |
|
15 |
| LM-DUST-DIFF | e- |
|
2 |
This case corresponds to the cloud at the initial stage of the protostellar
collapse (
![]() cm-3). For pure gas-phase chemistry and
high initial metal abundances (HM-GAS-DIFF), the dominant ions during most
of the 107 years are S+ and Mg+. We found that it is sufficient to
consider only these ions as important species in the species-based reduction
method. Taking sulphur to be the only important species, we can reduce the
number of species from 395 to 123 and achieve a computational speed gain of a
factor of about 25 with uncertainty of
cm-3). For pure gas-phase chemistry and
high initial metal abundances (HM-GAS-DIFF), the dominant ions during most
of the 107 years are S+ and Mg+. We found that it is sufficient to
consider only these ions as important species in the species-based reduction
method. Taking sulphur to be the only important species, we can reduce the
number of species from 395 to 123 and achieve a computational speed gain of a
factor of about 25 with uncertainty of ![]()
![]() at
at ![]() years (see
Fig. 3, middle and bottom panels, squares). If we consider both
ionised magnesium and ionised sulphur to be important species, the number of
species in the reduced set is 126, and the accuracy is better than
years (see
Fig. 3, middle and bottom panels, squares). If we consider both
ionised magnesium and ionised sulphur to be important species, the number of
species in the reduced set is 126, and the accuracy is better than ![]() during the entire evolution (see Fig. 3, middle and bottom panels,
stars). The computational gain is almost the same (see Table 3).
Note that metals other than magnesium (i.e., sodium and iron) are almost
equally important for the ionisation degree. But as they enter the chemical
network in a similar way, it is sufficient to designate magnesium to be
an important species in order to include in the reduced set all the
species that are needed to compute abundances of Na and Fe as well.
during the entire evolution (see Fig. 3, middle and bottom panels,
stars). The computational gain is almost the same (see Table 3).
Note that metals other than magnesium (i.e., sodium and iron) are almost
equally important for the ionisation degree. But as they enter the chemical
network in a similar way, it is sufficient to designate magnesium to be
an important species in order to include in the reduced set all the
species that are needed to compute abundances of Na and Fe as well.
With the reaction-based reduction technique, we choose electrons to be the
only important species. In this case the number of necessary species is 58,
which is more than two times smaller compared to the species-based reduction.
Additionally, the number of chemical reactions is reduced from 3864 to 111
(see Fig. 3, top panel). The achieved computational time gain is
of the order of 500, while the resulting uncertainties are by definition smaller
than ![]() during all 107 years of the evolution (see Table 3).
It should be recalled that the accuracy is preset in the reaction-based reduction,
so in all figures we only show relative errors for the species-based technique.
during all 107 years of the evolution (see Table 3).
It should be recalled that the accuracy is preset in the reaction-based reduction,
so in all figures we only show relative errors for the species-based technique.
The small number of necessary reactions in the reduced network can be explained by the fact that in this case the chemistry is governed by a rather restricted set of ionisation-recombination processes. Such a set is easily extracted from the entire network by the reaction-based selection algorithm. The fundamental reactions during the entire evolution time are the ionisation of molecular hydrogen and helium by cosmic rays and ionisation of carbon and sulphur by cosmic ray induced UV photons. These ions rapidly react with abundant molecules by efficient ion-molecule reactions, forming complex molecular ions, like HCO+. In turn, these molecular ions transfer charge to metal atoms. As metal ions are less chemically active, they become the most abundant charged species, regulating the fractional ionisation (Oppenheimer & Dalgarno 1974).
The situation is more complicated from the chemical point of view when
the initial metallicity is low. In the absence of abundant metals, the role
of electron suppliers goes to H3+, HCO+, and C+, involved in a
rich chemistry. Even though H+3 is the dominant ion, it alone does not
determine the ionisation degree with enough accuracy which is illustrated
in Fig. 3 (middle and bottom panels, circles). When this ion
only is considered to be an important species in the species-based reduction,
errors are negligible only at earlier times when the chemistry is relatively
simple. However, after 104 years the errors grow significantly, exceeding
a factor of 3 at the end of the computation. To account for later chemistry,
one has to take into account another important ion, HCO+. When these two
species are designated as important, errors do not exceed ![]() during the
entire computational time (crosses in middle and bottom panels in
Fig. 3). However, due to the complicated chemical connections
of the two ions, the species set reduction is only modest in this case. Less
than one hundred species can be excluded from the set with a reduction of
the computational time by a factor of 3 only (see Table 3).
during the
entire computational time (crosses in middle and bottom panels in
Fig. 3). However, due to the complicated chemical connections
of the two ions, the species set reduction is only modest in this case. Less
than one hundred species can be excluded from the set with a reduction of
the computational time by a factor of 3 only (see Table 3).
Not all the reactions involving these ions are important, though. With the reaction-based reduction method, we succeed in isolating a three time smaller set of 73 species involved in 169 reactions which are needed to follow the evolution of the ionisation degree in this case. It decreases the time, needed for the computation, by a factor of 500 (see Table 3). The slightly larger number of the necessary species and reactions in this case compared to the case of high metal initial abundances can be explained by more diverse chemistry involving interactions of complex species. The accuracy of the computed ionisation degree is again better than 30%.
Inclusion of accretion and desorption processes as well as surface reactions into these models does not lead to any noticeable changes, primarily, because the density is too low to produce significant ice mantles. Results of the species-based method show that it is possible to use the same reduced set in HM-GAS-DIFF, HM-GAD-DIFF, and HM-DUST-DIFF models without significant loss of accuracy. The same is true for the low metallicity models. However, applying the reaction-based approach to the gas-grain chemical network including surface reactions (DUST-DIFF), we found only moderate reduction as nearly half of the species have to be retained in the reduced network. The reason is that the surface reactions have very high rates compared to the gas-phase reactions and due to the selectivity of the reaction-based method many of them are designated to remain in the reduced network. This leads to the larger number of chemical species and reactions in such a network compared to the pure gas-phase case and, consequently, to the smaller computational time gains, which are about a factor of ten in this case (see Table 3).
When no gas-dust interaction is taken into account, the case of a dense
cloud (
![]() cm-3) at high metallicity is qualitatively
similar to the low-density case. Metals are again the dominant ions.
To compute their abundances (and hence the ionisation degree) with better
than 50% mean accuracy one needs to include sodium only to the list of
important species in the case of the species-based reduction. The reduced
set contains 72 species and provides two orders of magnitude gain in
computational speed. To further improve accuracy we add sulphur to the list
of important species. With the reduced set of 121 species we obtain
errors less than 10% during the entire computational time. The
reaction-based technique gives similar results and produces a reduced
network consisting of 131 species and 313 reactions with the same
computational gain. The difference between the high- and low-metallicity
cases is smaller for a dense cloud than for a diffuse cloud. In a denser
environment such chemically active ions as H+3 and HCO+ are less
abundant, and metal ions dominate the ionisation degree both in high- and
low-metallicity cases. As a result of this similarity, in a dense cloud for
the high and low metallicities the reduced species sets are nearly the same
both for the species- and reaction-based approaches, with similar errors
and computational gains (see Table 4).
cm-3) at high metallicity is qualitatively
similar to the low-density case. Metals are again the dominant ions.
To compute their abundances (and hence the ionisation degree) with better
than 50% mean accuracy one needs to include sodium only to the list of
important species in the case of the species-based reduction. The reduced
set contains 72 species and provides two orders of magnitude gain in
computational speed. To further improve accuracy we add sulphur to the list
of important species. With the reduced set of 121 species we obtain
errors less than 10% during the entire computational time. The
reaction-based technique gives similar results and produces a reduced
network consisting of 131 species and 313 reactions with the same
computational gain. The difference between the high- and low-metallicity
cases is smaller for a dense cloud than for a diffuse cloud. In a denser
environment such chemically active ions as H+3 and HCO+ are less
abundant, and metal ions dominate the ionisation degree both in high- and
low-metallicity cases. As a result of this similarity, in a dense cloud for
the high and low metallicities the reduced species sets are nearly the same
both for the species- and reaction-based approaches, with similar errors
and computational gains (see Table 4).
| Model | Important | Reduced | Speed |
| species | network | gain | |
| Species-based reduction | |||
| HM-GAS-DENS | Na+ |
|
|
| HM-GAS-DENS | Na+, S+ |
|
|
| LM-GAS-DENS | Na+ |
|
|
| LM-GAS-DENS | Na+, S+ |
|
|
| Reaction-based reduction | |||
| HM-GAS-DENS | e- |
|
130 |
| LM-GAS-DENS | e- |
|
55 |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{ms3106f4.eps}\end{figure}](/articles/aa/full/2003/07/aa3106/Timg66.gif) |
Figure 4: Ionisation degree (top and middle panels) and relative errors (bottom panel) in a dense cloud, computed with the full and reduced networks for gas-phase chemistry including accretion and desorption processes and dust surface reactions. Top panel reproduces results of the reaction-based reduction for the DUST-DENS model. Indicated are the "exact'' solutions for high (dotted line) and low (solid line) metallicities as well as the solution for the reduced species sets (HM - dashed line, LM - long-dashed line). Middle and bottom panels illustrate results of the species-based reduction for the GAD-DENS model. Shown are the "exact'' solutions (HM - dashed line, LM - solid line) and the solutions for various reduced sets (see text). |
| Open with DEXTER | |
The situation changes drastically, when gas-grain interactions are taken into account. In the high-metallicity case, at early stages of the evolution, the dominant ions are the same as in the diffuse medium, i.e., metals. However, after 104 years their depletion becomes important, and the dominant ions are H3+, HCO+, and N2H+. The straightforward use of the species-based criterion under such conditions leads to the significant loss of accuracy at this time. The problem is that this criterion is based on the selection of species whose abundances are needed to compute the abundance of an important species. But the depletion case is not that simple. Abundances of mantle species with high desorption energies are definitely not important and do not have to be computed with any accuracy. Based on the formal criterion (10), these species are to be excluded from the reduced set. However, this leads to the exclusion of the corresponding accretion reactions from the network, and counterparts of the excluded mantle species remain in the gas phase, significantly altering its chemistry.
With the species-based reduction method we investigated the GAD-DENS model,
i.e., the model in which accretion and desorption processes are taken into
account in addition to gas-phase chemistry. As we have no formal way to
select species whose absence in the gas phase is important to compute the
ionisation degree, we choose to check two artificial possibilities. First,
we add surface metals to the reduced network as they are primary contributors
to the electron abundance in the gas phase. Second, we allow all the selected
neutral species to stick to dust grains, reasoning that if their gas phase
abundances are deemed important then their depletion is important as well.
Results are shown in Fig. 4 (middle and bottom
panels). When only metal depletion (with a
handful of other species selected automatically) is taken into account the
errors are quite large, sometimes reaching ![]() .
To decrease errors,
depletion of all selected neutral species is needed. In the latter case, the
approximate solution differs from the "exact'' one by as much as
.
To decrease errors,
depletion of all selected neutral species is needed. In the latter case, the
approximate solution differs from the "exact'' one by as much as ![]() but
later on the difference is much smaller dropping to just a few per cent at
t=107 years (see Table 5).
but
later on the difference is much smaller dropping to just a few per cent at
t=107 years (see Table 5).
The ambiguity of the previous selection procedure is not an issue in the
reaction-based approach which is specifically designed to find necessary
formation and destruction pathways rather than necessary species. As it was
mentioned above, this method of reduction treats gas-grain interactions and
surface reactions equally with gas-phase reactions. Thus, one does not have to
worry about which surface species to keep in a reduced set in order to estimate
the abundances of important species. Therefore, this method works much better in
the reduction of chemical networks involving complicated processes like gas-grains
interactions and surface reactions. With the reaction-based technique, we reduced
the number of species and reactions in the gas-grain chemical network involving
surface reactions (DUST-DENS). We were able to remove about half of the species
from the full gas-grain network and to reduce the number of reactions by a factor
of 5 (see Fig. 4, top panel). The reduction speeds up the
computation by a factor of 8 only (see Table 5). At times, earlier than
about 104 years, the ionisation degree is calculated with an accuracy better
than ![]() .
At t>104 years, the uncertainties grow but remain less than
.
At t>104 years, the uncertainties grow but remain less than ![]() .
The reason is that it is more difficult to follow the evolution of the ionisation
degree with the reduced network, since the importance of the complicated gas-grain
interactions and surface reactions is raising up. In the low-metallicity case
(LM-GAD-DENS), which is more complex from the chemical point of view, the
reaction-based approach produces a reduced network that consists of 291 species
and 924 reactions and predicts an ionisation degree with a requested accuracy of
.
The reason is that it is more difficult to follow the evolution of the ionisation
degree with the reduced network, since the importance of the complicated gas-grain
interactions and surface reactions is raising up. In the low-metallicity case
(LM-GAD-DENS), which is more complex from the chemical point of view, the
reaction-based approach produces a reduced network that consists of 291 species
and 924 reactions and predicts an ionisation degree with a requested accuracy of
![]() during the entire evolutionary time. It accelerates the computations by a
factor of 7 (see Table 5).
during the entire evolutionary time. It accelerates the computations by a
factor of 7 (see Table 5).
Comparison of top (DUST) and middle (GAD) panels in Fig. 4 shows
that there is a difference between the evolution of ionisation degree in the case
of gas-grain chemistry with and without surface reactions. When surface
reactions are accounted for, fractional ionisation drops to 10-9 in
![]() years. In the case of gas-phase chemistry with accretion and
desorption it reaches the same equilibrium value later, after 105 years. Also,
the maximum value of the ionisation degree is higher in the latter case. Thus, we
conclude that surface reactions are important for the accurate estimation of the
fractional ionisation in dense molecular clouds at late stages of their evolution.
years. In the case of gas-phase chemistry with accretion and
desorption it reaches the same equilibrium value later, after 105 years. Also,
the maximum value of the ionisation degree is higher in the latter case. Thus, we
conclude that surface reactions are important for the accurate estimation of the
fractional ionisation in dense molecular clouds at late stages of their evolution.
To conclude this section, we emphasise that the reaction-based technique is more suitable for the reduction of gas-phase or gas-grain chemical networks if one intends to follow the evolution of the ionisation degree in diffuse or dense molecular clouds with a relatively small number of chemical species and reactions and a reasonable accuracy than it is the case for the species-based scheme.
| Model | Important | Reduced | Speed |
| species | network | gain | |
| Species-based reduction | |||
| HM-GAD-DENS | H+3, |
|
|
| surface metals | |||
| HM-GAD-DENS | H+3, |
|
|
| all surface | |||
| LM-GAD-DENS | H+3, |
|
|
| surface metals | |||
| LM-GAD-DENS | H+3, |
|
|
| all surface | |||
| Reaction-based reduction | |||
| HM-DUST-DENS | e- |
|
8 |
| LM-DUST-DENS | e- |
|
7 |
Essentially the same scheme of reduction, as in the previous section, is utilised for CO as well. First, the chemical model is computed with one of the full chemical networks. Its results are used to select key species needed to predict the CO abundance. Then the validity of a reduced network is checked by comparing the abundances obtained with the full and reduced networks for the entire evolutionary time. In all cases, we assumed that the CO molecule is the only important species. Results of the reduction and relevant computational speed gains are presented in Tables 6-9.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{ms3106f5.eps}\end{figure}](/articles/aa/full/2003/07/aa3106/Timg77.gif) |
Figure 5: The CO abundances (top and middle panels) and relative errors (bottom panel) in a diffuse cloud, computed with the full and reduced species set for pure gas-phase chemistry (GAS-DIFF model). Top panel reproduces results of the reaction-based reduction. Indicated are the "exact'' solutions (HM - dotted line, LM - solid line) and the solution for the case when CO is considered to be the only important species (HM - dashed line, LM - long-dashed line). The middle and bottom panels illustrate results of the species-based reduction. Shown are the "exact'' solutions (HM - dashed line, LM - solid line) and the solution for the case when CO is an important species (HM - open squares, LM - open circles). |
| Open with DEXTER | |
In the case of pure gas-phase chemistry in a diffuse cloud (at
the gas density
![]() cm-3, GAS-DIFF) the main processes,
relevant to the evolution of carbon monoxide, are its destruction by cosmic
rays or by cosmic ray induced photons and its production through the
neutral-neutral reactions of oxygen with carbon atoms and various light
carbon-bearing molecules, dissociative recombination of HCO+, and
destruction of H2CO by CR-induced photons. Since metals as well as S, Si, P, and Cl do not affect the evolution of CO abundances directly, it is natural to
expect that there should not be large differences between the high- and low-
metallicity cases.
cm-3, GAS-DIFF) the main processes,
relevant to the evolution of carbon monoxide, are its destruction by cosmic
rays or by cosmic ray induced photons and its production through the
neutral-neutral reactions of oxygen with carbon atoms and various light
carbon-bearing molecules, dissociative recombination of HCO+, and
destruction of H2CO by CR-induced photons. Since metals as well as S, Si, P, and Cl do not affect the evolution of CO abundances directly, it is natural to
expect that there should not be large differences between the high- and low-
metallicity cases.
In the absence of gas-grain interactions the evolution of CO is
comparatively simple - during almost the entire evolutionary time its abundance
is steadily approaching the equilibrium value of about 10-4 which
is reached at ![]() 106 years (see Fig. 5,
top and middle panels).
106 years (see Fig. 5,
top and middle panels).
With the species-based reduction, of all 395 species we select only
36 species in the high-metallicity case and 27 species in the case of low metal
abundances (see Fig. 5, middle panel). Due to the small size of
these reduced networks, time needed to solve the relevant ODE system is negligible,
less than a few seconds (see Table 6). At early evolutionary phase
(
![]() years) the uncertainties of the CO abundance can reach 50% for
high metallicity and 80% for low metallicity. Later, when the equilibrium abundance
is reached, error drops to about 20% (see Fig. 5, bottom panel).
The reason for the high uncertainty at early times is that such rare species as
CH3CO+ and CH2CO, which are not recognised by the species-based algorithm
to be necessary species, are in fact important at the early evolutionary phase for
the accurate estimation of the CO abundance.
years) the uncertainties of the CO abundance can reach 50% for
high metallicity and 80% for low metallicity. Later, when the equilibrium abundance
is reached, error drops to about 20% (see Fig. 5, bottom panel).
The reason for the high uncertainty at early times is that such rare species as
CH3CO+ and CH2CO, which are not recognised by the species-based algorithm
to be necessary species, are in fact important at the early evolutionary phase for
the accurate estimation of the CO abundance.
Applying the reaction-based reduction, we are able to follow the evolution of
the CO abundance for 107 years with an accuracy better than ![]() .
However, the price to pay for this is a significant number of
species to be held in the corresponding reduced networks. One needs to keep 158 and 95 species in the reduced networks for high and low metallicities,
respectively (see Fig. 5, top panel). The relevant computational
speed gain is a factor of 50 for the HM case and about 200 for the LM case (see
Table 6). It can be seen from Fig. 5 (top and middle
panels), that the CO abundances in the case of high- and low-metallicities do behave
similarly. Nevertheless, from the chemical point of view the case of low initial
abundances of metals is somewhat simpler in comparison with the high metallicity case
and implies smaller number of species and reactions to be kept in the reduced network.
.
However, the price to pay for this is a significant number of
species to be held in the corresponding reduced networks. One needs to keep 158 and 95 species in the reduced networks for high and low metallicities,
respectively (see Fig. 5, top panel). The relevant computational
speed gain is a factor of 50 for the HM case and about 200 for the LM case (see
Table 6). It can be seen from Fig. 5 (top and middle
panels), that the CO abundances in the case of high- and low-metallicities do behave
similarly. Nevertheless, from the chemical point of view the case of low initial
abundances of metals is somewhat simpler in comparison with the high metallicity case
and implies smaller number of species and reactions to be kept in the reduced network.
Inclusion of accretion-desorption processes and surface reactions does not
affect the chemistry in a diffuse cloud significantly. As we already mentioned in
Sect. 4.1, the gas-grain interactions are not efficient at such low
density (
![]() cm-3) since the typical rate of collisions
between dust grains and gas species is far too low. Using the species-based approach,
we found that it is enough to retain only 37 species for the high metal initial
abundances and 27 species in the LM case (see Table 6). These are almost
the same numbers as in the case of pure gas-phase chemistry. In fact, one
can use the same reduced sets of species and reactions in the GAS-DIFF, GAD-DIFF,
and DUST-DIFF models (separately for each metallicity set). However, uncertainties
in the computed CO abundances in all cases exceed 50% at
cm-3) since the typical rate of collisions
between dust grains and gas species is far too low. Using the species-based approach,
we found that it is enough to retain only 37 species for the high metal initial
abundances and 27 species in the LM case (see Table 6). These are almost
the same numbers as in the case of pure gas-phase chemistry. In fact, one
can use the same reduced sets of species and reactions in the GAS-DIFF, GAD-DIFF,
and DUST-DIFF models (separately for each metallicity set). However, uncertainties
in the computed CO abundances in all cases exceed 50% at ![]() 103-104 years.
103-104 years.
It is not that easy to remove these uncertainties. The application of the reaction-based method allows to cut the entire 543 species set by a factor of 2 in this case (see Table 6). It is more than two times the number of species found to be necessary for the correct reproduction of CO abundances in the case of pure gas-phase chemistry. Consequently, it speeds up the calculations by a factor of 5 only. The reason is, as noted in the previous section, that the reaction-based algorithm tends to keep some surface reactions in the reduced networks. Obviously, it leads to the larger number of species to be retained in the relevant reduced networks compared to the case of pure gas-phase chemistry.
| Model | Important | Reduced | Speed |
| species | network | gain | |
| Species-based reduction | |||
| HM-GAS-DIFF | CO |
|
>100 |
| LM-GAS-DIFF | CO |
|
>100 |
| HM-GAD-DIFF | CO |
|
>100 |
| LM-GAD-DIFF | CO |
|
>100 |
| Reaction-based reduction | |||
| HM-GAS-DIFF | CO |
|
50 |
| LM-GAS-DIFF | CO |
|
240 |
| HM-DUST-DIFF | CO |
|
8 |
| LM-DUST-DIFF | CO |
|
5 |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{ms3106f6.eps}\end{figure}](/articles/aa/full/2003/07/aa3106/Timg88.gif) |
Figure 6: Same as in Fig. 5 but for a dense cloud (GAS-DENS). |
| Open with DEXTER | |
In a dense molecular cloud (
![]() cm-3) the main processes
leading to the production and destruction of CO molecules in the case of pure
gas-phase chemistry (GAS-DENS) are the same as in a diffuse cloud, but with
one important change. At such high density, the role of chemical reactions
involving abundant species like C, O, CH, and CH2, becomes even more important.
Therefore, we may expect that in this case the chemistry relevant to the evolution
of carbon monoxide is even simpler than in the diffuse cloud (GAS-DIFF). It
implies a smaller set of necessary species.
cm-3) the main processes
leading to the production and destruction of CO molecules in the case of pure
gas-phase chemistry (GAS-DENS) are the same as in a diffuse cloud, but with
one important change. At such high density, the role of chemical reactions
involving abundant species like C, O, CH, and CH2, becomes even more important.
Therefore, we may expect that in this case the chemistry relevant to the evolution
of carbon monoxide is even simpler than in the diffuse cloud (GAS-DIFF). It
implies a smaller set of necessary species.
The results of reduction for this case are shown in Fig. 6.
The CO abundance increases rapidly at early evolutionary
stages (![]() years). Later, when the chemical equilibrium is reached,
it remains constant around 10-4.
years). Later, when the chemical equilibrium is reached,
it remains constant around 10-4.
Using the species-based reduction technique, we succeeded in the isolation of a
small set of 27 species allowing us to follow the evolution of CO with a very
good accuracy <![]() for all 107 years for both the high- and low-metallicity
case (see Fig. 6, middle and bottom panels). Again, the computational
time is negligibly small, less than a second (see Table 7).
for all 107 years for both the high- and low-metallicity
case (see Fig. 6, middle and bottom panels). Again, the computational
time is negligibly small, less than a second (see Table 7).
But even this 27 species set contains excessive information.
Applying the reaction-based reduction approach, we revealed that in reality
there are only 8 species involved in 9 reactions which are necessary for
the accurate estimation of CO abundances during the entire evolutionary time
(see Fig. 6, top panel). The relevant reduced network is given
in Table 8. The uncertainties of computed CO abundances do not exceed
![]() for all 107 years of the evolution.
This remarkable result, showing the power of the reaction-based technique,
explains why there is no difference between the cases of high and low metals in a
dense cloud: metals are completely excluded from this network.
for all 107 years of the evolution.
This remarkable result, showing the power of the reaction-based technique,
explains why there is no difference between the cases of high and low metals in a
dense cloud: metals are completely excluded from this network.
In the medium with the atomic initial composition (except for molecular hydrogen)
reactions start from the dissociation of H2 molecules by cosmic ray particles
and from their radiative association with atomic carbon. The latter reaction leads to
CH2 formation. This molecule reacts with atomic H and C leading to
CH and C2H. These three molecules (CH, CH2, and C2H) associate with atomic
oxygen finally producing the CO molecule. These processes are balanced by destruction
of CO and CH by CR-induced photons. In this way, the key reaction pathways can be
isolated for which high-quality experimental reaction rate measurements have to be
provided for an accurate modelling. It may seem to be somewhat surprising that
the reduced network does not contain HCO+, at variance with the diffuse cloud case.
Note, however, that the maximum value of the HCO+ abundance reached in the
high-density model (![]() 10-10) is two orders of magnitude less than in
the diffuse cloud model. Given the correspondingly low electron abundance, this prevents
effective CO synthesis in dissociative recombination of HCO+. Proton transfer reactions
of CO with H2+ and H3+ that would transform CO to HCO+ are also nearly
quenched due to low abundances of these ions. Thus, while CO is definitely an
important species for HCO+ in a dense medium, the opposite is not true.
10-10) is two orders of magnitude less than in
the diffuse cloud model. Given the correspondingly low electron abundance, this prevents
effective CO synthesis in dissociative recombination of HCO+. Proton transfer reactions
of CO with H2+ and H3+ that would transform CO to HCO+ are also nearly
quenched due to low abundances of these ions. Thus, while CO is definitely an
important species for HCO+ in a dense medium, the opposite is not true.
Going somewhat out of the scope of the present paper, we mention briefly that this
network proved to be valid under a much wider range of conditions that are described
here. Calculations that will be presented in a subsequent paper show that it can be
used for estimating the CO abundance not only in dark dense clouds, but in a
translucent (
![]() mag) medium as well. It gives less than 50% error at
mag) medium as well. It gives less than 50% error at
![]() cm-3 and T<250 K and can be used in a denser medium
as well (
cm-3 and T<250 K and can be used in a denser medium
as well (
![]() cm-3) provided
cm-3) provided
![]() K and
K and
![]() mag, conditions being typical of hot cores or protoplanetary discs.
mag, conditions being typical of hot cores or protoplanetary discs.
The accuracy of this network is also insensitive to the variation of the adopted C/O ratio (0.43) within a factor of a few. The value of this ratio would be critical, though, in the attempt to construct a reduced network for carbon or oxygen separately. If carbon is less abundant than oxygen (as in the adopted abundance sets), all C atoms are locked in CO molecules, and the reduction is rather effective. In fact, it is possible to construct a single network of a few tens of species that reproduces abundances of C, O, and CO simultaneously with less than 100% uncertainty. If the C/O ratio is greater than 1, extra carbon is available for producing long carbon chains, and the effective reduction (with C as an important species) is not possible.
| Model | Important | Reduced | Speed |
| species | network | gain | |
| Species-based reduction | |||
| HM-GAS-DENS | CO |
|
>100 |
| LM-GAS-DENS | CO |
|
>100 |
| Reaction-based reduction | |||
| HM-GAS-DENS | CO | >104 | |
| LM-GAS-DENS | CO | >104 | |
| Reactions | ||
| 1 H + CH2 |
|
CH + H2 |
| 2 H2 + C |
|
CH2 + PHOTON |
| 3 C + CH2 |
|
C2H + H |
| 4 O + CH |
|
CO + H |
| 5 O + CH2 |
|
CO + H + H |
| 6 O + C2H |
|
CO + CH |
| 7 H2 + CRP |
|
H + H |
| 8 CH + CRPHOT |
|
C + H |
| 9 CO + CRPHOT |
|
C + O |
The situation is no longer trivial when gas-grain interactions and surface reactions are taken into account (GAD-DENS and DUST-DENS). The influence of these processes on the evolution of abundances is twofold. First, the freeze-out of the gas-phase CO leads to the activation of certain chemical reaction chains that are suppressed in the presence of CO. Second, the presence of CO in icy mantles can drive some surface reactions that may eventually result in the formation of complex organic species.
In the absence of surface reactions the evolution of carbon monoxide is
simple (see Fig. 7, middle panel). First, its abundance grows
steadily, at
![]() years reaching a value of
years reaching a value of ![]()
![]() .
Then the gas-grain interaction becomes important, and the CO molecules heavily
deplete from the gas phase, forming significant mantles. The chemical equilibrium
is reached at 105 years with the gas-phase CO abundance of a few times 10-8.
.
Then the gas-grain interaction becomes important, and the CO molecules heavily
deplete from the gas phase, forming significant mantles. The chemical equilibrium
is reached at 105 years with the gas-phase CO abundance of a few times 10-8.
The species-based reduction technique isolates two sets to be used in the high-
and low-metallicity cases of the GAD-DENS model. But in fact these sets are very similar
to each other, and one can use the same set containing about 30 species with high- and
low- initial metallicities both in pure gas-phase models and with accretion/desorption
taken into account. The resulting uncertainties are smaller than ![]() for both
metallicity cases (see Fig. 7, bottom panel).
Again, the computational time which is necessary to compute the evolution of
CO is negligibly small.
for both
metallicity cases (see Fig. 7, bottom panel).
Again, the computational time which is necessary to compute the evolution of
CO is negligibly small.
The evolution of carbon monoxide in the situation, when surface reactions
are considered, is shown in Fig. 7, top panel. The gas-phase
CO abundance increases at early times and reaches the value of ![]() 10-4at
10-4at ![]() years. Then, the depletion of CO becomes efficient. At
years. Then, the depletion of CO becomes efficient. At
![]() years the gas-phase CO abundance is determined by the balance
between accretion and desorption processes. Its value is almost the same as
the equilibrium CO abundance in the GAD-DENS model, i.e., a few times 10-8.
After 106 years surface re-processing of CO takes over. It is converted to
other species, mainly, CO2. At this stage the accretion of CO is no more
balanced by its desorption, and after some time the new, much lower
equilibrium value
years the gas-phase CO abundance is determined by the balance
between accretion and desorption processes. Its value is almost the same as
the equilibrium CO abundance in the GAD-DENS model, i.e., a few times 10-8.
After 106 years surface re-processing of CO takes over. It is converted to
other species, mainly, CO2. At this stage the accretion of CO is no more
balanced by its desorption, and after some time the new, much lower
equilibrium value ![]() 10-11 is established. Note that this behaviour is at least
partially caused by our simplified treatment of the gas-dust interactions. We adopt
the Hasegawa & Herbst (1993) value for CO binding energy which is estimated
for a SiO2 surface. In reality, after the CO mantle is formed, the binding energy of
CO and other molecules may become smaller, so that desorption is still competitive with
surface re-processing.
10-11 is established. Note that this behaviour is at least
partially caused by our simplified treatment of the gas-dust interactions. We adopt
the Hasegawa & Herbst (1993) value for CO binding energy which is estimated
for a SiO2 surface. In reality, after the CO mantle is formed, the binding energy of
CO and other molecules may become smaller, so that desorption is still competitive with
surface re-processing.
With the reaction-based reduction, we are able to select sets of 388 species and 1563 reactions for the high-metallicity case and 270 species and 798 reactions for the
low-metallicity case. The relevant computational gains are only about 3 and 16,
respectively (see Table 9). The error of the predicted CO abundances is
less than ![]() during the entire evolutionary time. The number of species which are
needed to estimate the CO abundance accurately in the high-metallicity case is again
during the entire evolutionary time. The number of species which are
needed to estimate the CO abundance accurately in the high-metallicity case is again
![]()
![]() larger compared to the low-metallicity case. Reduced networks with smaller
number of species are not usable in the calculations in this case. The reason is that
the relevant ODE systems are so stiff for the DVODE solver that the computational times
are much larger compared to the case of the full chemical network.
larger compared to the low-metallicity case. Reduced networks with smaller
number of species are not usable in the calculations in this case. The reason is that
the relevant ODE systems are so stiff for the DVODE solver that the computational times
are much larger compared to the case of the full chemical network.
| Model | Important | Reduced | Speed |
| species | network | gain | |
| Species-based reduction | |||
| HM-GAD-DENS | CO |
|
>100 |
| LM-GAD-DENS | CO |
|
>100 |
| Reaction-based reduction | |||
| HM-DUST-DENS | CO |
|
3 |
| LM-DUST-DENS | CO |
|
16 |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{ms3106f7.eps}\end{figure}](/articles/aa/full/2003/07/aa3106/Timg108.gif) |
Figure 7: Same as in Fig. 6 but for the DUST-DENS ( top panel) and GAD-DENS ( middle and bottom panels) models. |
| Open with DEXTER | |
Concluding this section, we emphasise that if surface reactions are
considered in a chemical network, then its reduction for carbon monoxide is of
no practical use as the relevant computational speed gains are too small.
However, if accretion and desorption of species are taken into account as the
only gas-grain processes, then it is possible to find a few tens in half
a thousand species which must be kept in a reduced network in order to follow
the evolution of CO without significant (![]()
![]() )
errors.
)
errors.
The purpose of the present paper is to check whether a typical astrochemical database contains redundant information that can be ignored in certain calculations regarding interstellar chemistry. The primary incentive for our work is the long time usually needed to complete a more or less detailed model of interstellar chemistry in dynamically evolving media. In many cases the evolution of only a few or even one species are of the main interest for an astronomer. The notable example is the degree of ionisation in dense interstellar clouds which is regulated by the abundances of a few dominant ions. It has been shown by many authors that in this case the relevant chemistry is governed by a rather restricted set of chemical processes (e.g. Oppenheimer & Dalgarno 1974; Ciolek & Mouschovias 1995).
Of course, one needs a mathematically rigorous way to "extract''
only those species and reactions from the entire network that are needed
to reproduce the evolution of a species under investigation within a reasonable numerical
accuracy (say, <![]() ). Such a reduction would decrease the number of species in the
network and, hence, the relevant computational time. Using the DVODE solver, we found that
this time is proportional to roughly the third power of the number of the involved
chemical species. Thus, by decreasing the number of species in the model by just a factor
of two, one can obtain an order of magnitude computational speed gain! Besides, the
reduction would help to understand the role of a particular chemical compound or reaction
for the evolution of an important species. However, one must bear in mind that the cost of
the reduction is that the relevant reduced network has a certain range of applicability,
i.e. it gives reliable estimates on the abundances of an important species for a specific
range of the gas temperature, density, etc.
). Such a reduction would decrease the number of species in the
network and, hence, the relevant computational time. Using the DVODE solver, we found that
this time is proportional to roughly the third power of the number of the involved
chemical species. Thus, by decreasing the number of species in the model by just a factor
of two, one can obtain an order of magnitude computational speed gain! Besides, the
reduction would help to understand the role of a particular chemical compound or reaction
for the evolution of an important species. However, one must bear in mind that the cost of
the reduction is that the relevant reduced network has a certain range of applicability,
i.e. it gives reliable estimates on the abundances of an important species for a specific
range of the gas temperature, density, etc.
The first mathematically proven reduction of astrochemical networks is
made by RRPHH. Their intention was to isolate a set of species and reactions which are
needed to follow the evolution of the CO abundance within the 30% accuracy.
They considered physical conditions, typical of translucent regions, i.e.,
![]() cm-3, T=10 K,
cm-3, T=10 K,
![]() mag, with
"low metal'' initial abundances. They discriminated 69 necessary species participating
in 241 reactions from the Ohio New Standard Model, including reactions of
dissociative recombination on dust grains. They found that it is possible to decrease
further the number of necessary species and reactions to 33 and 116, respectively, by
the artificial modification of the network. It consisted in exclusion of all reactions
involving carbon chains longer than C2H2+ and in introduction instead of few
synthetic reactions to correctly predict the abundances of shorter carbon chains.
mag, with
"low metal'' initial abundances. They discriminated 69 necessary species participating
in 241 reactions from the Ohio New Standard Model, including reactions of
dissociative recombination on dust grains. They found that it is possible to decrease
further the number of necessary species and reactions to 33 and 116, respectively, by
the artificial modification of the network. It consisted in exclusion of all reactions
involving carbon chains longer than C2H2+ and in introduction instead of few
synthetic reactions to correctly predict the abundances of shorter carbon chains.
The same method was applied by RBHPR in order to identify reduced networks that
predict the degree of ionisation in interstellar clouds with less than 30% uncertainty
under a wide range of physical conditions. They reduced two networks, namely, a "full''
network of 218 species and 2747 reactions and a "large'' network of 79 species and
1026 reactions. In the "full'' network metals beside sodium were excluded, whereas the
"large'' network in addition excluded nitrogen and most species having more than two
nuclei heavier than hydrogen. High and low metal initial abundances were used.
They considered the following physical conditions: T=20 K,
![]() cm-3,
cm-3,
![]() mag. The small combined reduced
network having 28 species and 71 reactions was found for the case of low metallicity. In
the high metallicity case similar network of 29 species and 65 reactions was isolated with
the artificially simplified sulphur chemistry.
mag. The small combined reduced
network having 28 species and 71 reactions was found for the case of low metallicity. In
the high metallicity case similar network of 29 species and 65 reactions was isolated with
the artificially simplified sulphur chemistry.
We analysed the possibility of reducing the number of species and reactions in the UMIST 95 database by two different methods that we refer to as species-based and reaction-based techniques. Our primary goal is to compare the efficiency of these techniques under physical conditions typical of dark regions. We study the applicability of both methods in the case, when the complicated gas-grain interactions and the surface reactions are taken into account. Having in mind possible applications, we tried to make these methods as automatic as possible. Unlike RRPHH and RBHPR, we did not apply artificial modifications to the reduced networks. While such modifications can be useful in certain cases, usually it is not a trivial task and can be fraught with difficulties when a wide range of physical conditions is considered. Thus, we left the reduction entirely to the reduction techniques.
Both techniques proved to be efficient enough to reduce significantly gas-phase
chemical networks needed to compute the ionisation degree or CO abundance in diffuse and
dense molecular clouds with a reasonable accuracy of <![]() .
If the accretion-desorption
processes and surface reactions are accounted for, the reduction becomes less effective
since the relevant chemistry is too complicated. Even though the number of chemical
reactions in the reduced networks could be decreased by a few times, making their analysis
easier, the computational speed gains are too small in these models to make this reduction
of particular interest for chemo-dynamical modelling. Though, at least for the
ionisation degree, the situation may be alleviated by the fact that at high densities when
depletion is effective, grain charging processes are more important for the fractional
ionisation than the chemistry.
.
If the accretion-desorption
processes and surface reactions are accounted for, the reduction becomes less effective
since the relevant chemistry is too complicated. Even though the number of chemical
reactions in the reduced networks could be decreased by a few times, making their analysis
easier, the computational speed gains are too small in these models to make this reduction
of particular interest for chemo-dynamical modelling. Though, at least for the
ionisation degree, the situation may be alleviated by the fact that at high densities when
depletion is effective, grain charging processes are more important for the fractional
ionisation than the chemistry.
We found that the reaction-based technique is more effective compared to the species-based
technique (see Tables 3-5). The number of reactions is at least
three times smaller for the reaction-based reduction than for the species-based reduction
which is natural to expect as reaction rates are not discriminated in the latter method.
But the number of species is also smaller for the reaction-based technique in most models.
When the gas-dust interaction is taken into account, the reaction-based technique is even
more effective than the species-based technique, as it provides the simultaneous reduction
of the number of species and reactions and proper treatment of the gas-grain processes.
Unfortunately, it is impossible to compare our results for the ionisation degree directly
with the results of RBHPR. One reason is that they considered moderate values of visual
extinction
![]() mag, typical of translucent clouds, whereas we dealt with
obscured regions, where
mag, typical of translucent clouds, whereas we dealt with
obscured regions, where
![]() mag. Another issue is that RBHPR started the
reduction from a somewhat smaller "full'' network of 218 species and 2747 reactions,
while we considered the network of 395 species involved in 3864 reactions. Nonetheless,
the resulting reduced networks have comparable sizes, namely, 29 species and 65 reactions
(RBHPR, see Table 4) and 58 species and 111 reactions (this work, Table 3) in
the case of high metals. In the low metallicity case the reduced network by
RBHPR has 28 species involved in 71 reactions, compared to our network
of 73 species and 169 reactions.
mag. Another issue is that RBHPR started the
reduction from a somewhat smaller "full'' network of 218 species and 2747 reactions,
while we considered the network of 395 species involved in 3864 reactions. Nonetheless,
the resulting reduced networks have comparable sizes, namely, 29 species and 65 reactions
(RBHPR, see Table 4) and 58 species and 111 reactions (this work, Table 3) in
the case of high metals. In the low metallicity case the reduced network by
RBHPR has 28 species involved in 71 reactions, compared to our network
of 73 species and 169 reactions.
In the case of reduction made for CO, the situation is a bit more diverse. In a diffuse cloud with pure gas-phase chemistry, the species-based reduction technique overcomes the reaction-based method, but at the expense of higher uncertainties (see Table 6 and Fig. 5). In a dense cloud with pure gas-phase chemistry, the reaction-based technique allows us to extract the reduced network which is very small (Table 8) but still functional under a very wide range of physical conditions. This network is smaller than the one found by RRPHH, though it has been extracted from the larger full network. Also, it has a wider range of applicability.
The next question to ask is how to apply these methods in dynamical calculations. One can envisage two different strategies to pursue this goal. One way is to reduce the number of species and reactions at the outset and then to use the reduced network during the entire computational time. Another strategy would be to perform the network analysis in the "real-time'' mode, during the dynamical evolution.
The first strategy is obviously more cost-effective as it does not add any overhead to the computational time. The reduced network must be prepared in advance and checked against the range of physical conditions that are expected in the dynamical model. Of course, this check is only possible under simplified conditions (otherwise it makes no sense). For example, if the range of densities (temperatures) is expected in the model, one may check that the reduced network is valid at its upper and lower boundaries, hoping that it is valid as well for any densities (temperatures) in between. Of our two techniques, the reaction-based approach works in this mode, as to construct the reduced network the abundances during the entire evolutionary time are analysed. The resultant network accounts for both the early and later chemistry.
The second method seems to be more robust. After the ability of the reduction technique to remove the excessive information from the chemical network is checked, one can perform the reduction, for example, at each dynamical time step or even less often. The full chemical network must be taken into account every time, with current abundances, temperature, density, etc. One may want to identify not only species that can be ignored but species with quasi-stationary abundances as well. Our species-based reduction technique is well suited to be used at a given t with the current values of parameters because, as we mentioned above, the sharp jump in Bi values allow to distinguish necessary and unnecessary species clearly. Usually, there is no clear boundary between needed and unneeded reactions (see Fig. 2), so one has to readjust cut-off threshold several times before optimal reduction is found. Thus, in some cases, the reaction-based method is more time-consuming than the species-based approach which is critical if the method is to be invoked from the dynamical code more than once.
Neither method guarantees that the same accuracy, as found in test cases, is preserved during the real computations. With the first method one cannot be sure that conditions, under which the reduced network is not valid, are never met in the dynamical model. The second method properly takes into account the current conditions but is more sensitive to the history of abundance changes. Consider the ionisation degree in the dense cloud when freeze-out is taken into account (high-metallicity case). One of the dominant ions at later times is N2H+. As a necessary species, it is included in the network at the time when metal depletion becomes important (late stages). However, the abundance of this ion cannot be followed with any accuracy as it is absent in early-time reduced networks, and its entire previous evolution is lost. So, both strategies must be applied with care, taking into account possible uncertainties.
We note in passing that the decreased accuracy of the reduced networks may not be such an
issue. Many reactions in the UMIST 95 have poorly measured or estimated rates,
with typical uncertainties ![]()
![]() or more (Millar et al. 1997). This
introduces unknown global errors in the modelled species abundances. On the other hand,
modern observations usually provide column densities of abundant species with
uncertainties of few tens of percents. Therefore, at nearly all astrophysically important
situations accuracy of
or more (Millar et al. 1997). This
introduces unknown global errors in the modelled species abundances. On the other hand,
modern observations usually provide column densities of abundant species with
uncertainties of few tens of percents. Therefore, at nearly all astrophysically important
situations accuracy of ![]()
![]() seems to be quite appropriate.
seems to be quite appropriate.
We developed a robust method to reduce simultaneously the number of species and reactions in chemical networks. The straightforward application for such reduced chemical networks would be the modelling of the evolution of magnetised protostellar clouds or protoplanetary discs, when it is necessary to compute the fractional ionisation self-consistently with dynamical processes.
Investigating the applicability of this reduction approach, we considered the conditions of diffuse and dense molecular clouds and utilised the UMIST 95 database of chemical reaction rates. For the sake of comparison, we performed the same reduction with the objective reduction technique. The new reaction-based way of reduction proved to be more efficient and accurate but more time-consuming as well.
It is found that the number of species and reactions that
are needed to follow the evolution of the CO abundance or the ionisation degree can be
greatly decreased in the case of pure gas-phase chemistry, implying
computational speed gains of more than a few hundred. For instance, to follow accurately
(with <![]() uncertainty) the evolution of the CO abundance in a dense cloud, it is
enough to retain only 8 species involved in 9 reactions in the chemical network.
However, as soon as the gas-grain interactions and surface
chemistry are taken into account, reduction is modest and corresponding
acceleration factors are around 10.
uncertainty) the evolution of the CO abundance in a dense cloud, it is
enough to retain only 8 species involved in 9 reactions in the chemical network.
However, as soon as the gas-grain interactions and surface
chemistry are taken into account, reduction is modest and corresponding
acceleration factors are around 10.
Acknowledgements
DS was supported by the German Deutsche Forschungsgemeinschaft, DFG project "Research Group Laboratory Astrophysics'' (He 1935/17-1), the work of DW was supported by the INTAS grant YS 2001-1/91 and the RFBR grant 01-02-16206. We thank the anonymous referee for comments and suggestions.
We use the g77 compiler and SuSe Linux 7.3 installed on the Pentium IV 2 GHz, 1 GB RAM PC as well as Compaq Visual Fortran 6.5 compiler on Pentium III, 850 MHz, 256 MB RAM PC. The typical time necessary to run a model is only a few minutes in the case of gas-phase chemistry and can reach half an hour if the gas-grain interactions are taken into account.