

Up: Distribution of star-forming complexes
![\begin{figure}
\includegraphics[width=8.8cm]{MS3024f07a.ps}\hspace*{4mm}\includegraphics[width=8.5cm]{MS3024f07b.ps}\end{figure}](/articles/aa/full/2003/05/aa3024/Timg48.gif) |
Figure 7:
Left: cumulative number vs. aperture radius for the
detected lumps within selected galaxies. Logarithms are given to
base 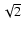 .
The slope of the straight parts gives the cluster
dimension. Fat lines represent large-scale length (and high-lump
number) galaxies, thin lines short-scale length (and low-lump number)
galaxies. Right: reduced bright-lump cluster dimension
vs. extrapolated central surface brightness. The symbol size indicates
the number of lumps used for the determination of the observed
(non-reduced) cluster dimension. The line corresponds to a bisector
fit to the data (equation given in the text). .
The slope of the straight parts gives the cluster
dimension. Fat lines represent large-scale length (and high-lump
number) galaxies, thin lines short-scale length (and low-lump number)
galaxies. Right: reduced bright-lump cluster dimension
vs. extrapolated central surface brightness. The symbol size indicates
the number of lumps used for the determination of the observed
(non-reduced) cluster dimension. The line corresponds to a bisector
fit to the data (equation given in the text). |
Star-forming complexes in dwarf galaxies form non-random point
patterns also in a sense different from that discussed in Sect. 4.3. Their positions correlate according to a self-similar
(fractal) arrangement. In this section we substantiate this claim
studying an index devoted to spatial statistics, namely the
correlation or clustering dimension, as applied to two-dimensional
bright-lump distributions.
As observed by Elmegreen & Elmegreen (2001), the distribution of
bright-lump center positions on a kiloparsec scale in spiral and
irregular galaxies obey a power-law behaviour similar to the fractal
structure of the interstellar gas with fractal dimension D3=2.3.
Thus the center positions of star-forming aggregates within isolated areas of large galaxies are fractal. Here we address the
question whether star-forming complexes that are scattered over the
entire disks of dwarf galaxies are non-randomly distributed as
well. We restrict our inquiry to the dwarfs of our sample that exhibit
more than 20 bright lumps. Given our photometry with image scales of
typically well above 10 parsecs/pixel and seeing conditions of a few
pixels we expect to only dissolve structures larger than
about 100 parsecs. Thus small-scale clustering and the accompagning blending
effects (Elmegreen & Elmegreen 2001) are of no concern to our
study. To quantify the spatial clustering of the position patterns we
adopt the cumulative distance method (Hastings & Sugihara 1996): a
power law relationship
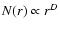 is assumed for the
cumulative number of points N(r) within a distance r around each
point. If the distribution is (at least partially) self-similar this
will be manifested in a
is assumed for the
cumulative number of points N(r) within a distance r around each
point. If the distribution is (at least partially) self-similar this
will be manifested in a 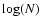 -
-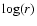 diagram as a straight line
with slope D, called the cluster (or correlation) dimension,
diagram as a straight line
with slope D, called the cluster (or correlation) dimension,
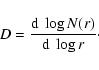
The more highly clustered the points
(at all relevant scales), the lower the cluster dimension. For a
random or Poissonian distribution of points on a two-dimensional plane
one has 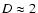 ,
independent of the number of points
involved, which only governs the error estimate. The graphs for six
observed galaxies with 20-30 lumps and for five galaxies with about
200-300 lumps are shown in Fig. 7, left, plotted with thin and
thick lines, respectively. For both groups the relevant scaling range,
i.e. the straight part of the curve, lies between about 100
(
,
independent of the number of points
involved, which only governs the error estimate. The graphs for six
observed galaxies with 20-30 lumps and for five galaxies with about
200-300 lumps are shown in Fig. 7, left, plotted with thin and
thick lines, respectively. For both groups the relevant scaling range,
i.e. the straight part of the curve, lies between about 100
(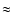
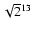 )
and 1000 (
)
and 1000 (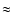
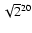 )
parsecs. The galaxies with lower lump numbers exhibit smaller
cluster dimensions (
)
parsecs. The galaxies with lower lump numbers exhibit smaller
cluster dimensions (
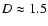 )
than the galaxies with many
detected lumps (
)
than the galaxies with many
detected lumps (
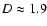 ). However, plotting D versus
). However, plotting D versus
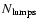 for all our data (not shown), no clear
relation between the two quantities is seen anymore. There
nevertheless is a hidden dependence between the two variables:
it emerges from the non-uniform distribution of lumps in
exponential-disk systems (as discussed in Sect. 4), and it is to be
corrected for. We do so by, first, simulating point patterns with
exponential radial number density distributions and indeed are
recovering the observed dependence of the cluster dimension on the
number of lumps. In particular, accepting a linear regression we
obtain
for all our data (not shown), no clear
relation between the two quantities is seen anymore. There
nevertheless is a hidden dependence between the two variables:
it emerges from the non-uniform distribution of lumps in
exponential-disk systems (as discussed in Sect. 4), and it is to be
corrected for. We do so by, first, simulating point patterns with
exponential radial number density distributions and indeed are
recovering the observed dependence of the cluster dimension on the
number of lumps. In particular, accepting a linear regression we
obtain
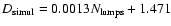 .
Actually, a function
converging asymptotically toward D=2 for large lump numbers would be
more appropriate; having no clue as to its exact form, though, we stay
within the linear approximation. Then, second, instead of using the
observed cluster dimensions as inferred from galaxy images, we
introduce reduced cluster dimensions defined by
.
Actually, a function
converging asymptotically toward D=2 for large lump numbers would be
more appropriate; having no clue as to its exact form, though, we stay
within the linear approximation. Then, second, instead of using the
observed cluster dimensions as inferred from galaxy images, we
introduce reduced cluster dimensions defined by
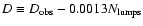 ,
i.e. all measured cluster dimensions are
made comparable by formally adjusting them to the common number
,
i.e. all measured cluster dimensions are
made comparable by formally adjusting them to the common number
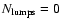 .
Other values could have been chosen; however, the
adopted value (or other low values, say
.
Other values could have been chosen; however, the
adopted value (or other low values, say
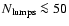 )
yields consistently cluster
dimensions of about or below the theoretical maximum value of two. We
show in Fig. 7, right, the reduced cluster dimension as a function of
the extrapolated central surface brightness for all galaxies. There is
a weak but significant trend that fainter dwarf galaxies exhibit
lower cluster dimensions, i.e. more strongly clustered star-forming
regions, than brighter dwarf galaxies. The same statement holds if
instead of central surface brightness we take the absolute magnitude
of the galaxy.
)
yields consistently cluster
dimensions of about or below the theoretical maximum value of two. We
show in Fig. 7, right, the reduced cluster dimension as a function of
the extrapolated central surface brightness for all galaxies. There is
a weak but significant trend that fainter dwarf galaxies exhibit
lower cluster dimensions, i.e. more strongly clustered star-forming
regions, than brighter dwarf galaxies. The same statement holds if
instead of central surface brightness we take the absolute magnitude
of the galaxy.
We have also determined the cluster dimensions for 15 selected
sub-galactic areas (consisting of about 30 lumps within a circle of
about 1.5 kpc diameter) within larger galaxies (each with a total of
more than about 200 lumps). With a mean of
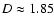 and a
scatter of only about 0.1, these areas show relatively high cluster
dimensions that are typically lying above their galaxies'
values. It furthermore implies that cluster dimensions for local
lump aggregates scatter less than those for entire galaxies.
and a
scatter of only about 0.1, these areas show relatively high cluster
dimensions that are typically lying above their galaxies'
values. It furthermore implies that cluster dimensions for local
lump aggregates scatter less than those for entire galaxies.
We now attempt to give an interpretation of the reduced cluster
dimension in terms of intragalactic gas porosity and star formation
rate. The volume filling factor f of the empty or low-density
regions of a self-similar medium, the porosity, can be related to the
medium's fractal dimension in three dimensions, D3, by
where 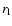 and
and 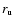 are the lower and upper boundary of the relevant scaling range (e.g.,
Turcotte 1992). From Fig. 7, left, and as mentioned above, we infer
are the lower and upper boundary of the relevant scaling range (e.g.,
Turcotte 1992). From Fig. 7, left, and as mentioned above, we infer
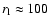 pc and
pc and
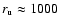 pc. This approach to galaxy
porosity is analogous to Elmegreen's (1997) treatment of fractal
interstellar gas clouds, the porosity of which was characterized by
pc. This approach to galaxy
porosity is analogous to Elmegreen's (1997) treatment of fractal
interstellar gas clouds, the porosity of which was characterized by
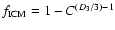 ,
with a maximum density contrast of
,
with a maximum density contrast of
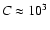 -104 for the intracloud gas. The two approaches are
formally and numerically similar if we identify
-104 for the intracloud gas. The two approaches are
formally and numerically similar if we identify
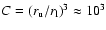 .
Qualitatively, dwarf irregular galaxies may thus be considered
as huge star-forming clouds similar to fractal intragalactic
star-forming clouds. Solving for the dimension, we obtain
.
Qualitatively, dwarf irregular galaxies may thus be considered
as huge star-forming clouds similar to fractal intragalactic
star-forming clouds. Solving for the dimension, we obtain
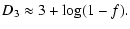 |
|
|
(3) |
Interpreting Fig. 7, right, in terms of galaxy porosity, we have to
take into account that the scaling dimension of a projected
isotropic self-similiar object is one less than the true dimension
(Elmegreen & Elmegreen 2001), thus D3=D+1. We then learn that on average fainter galaxies with on average lower cluster
dimensions, i.e. with stronger clustering properties, are also more
porous (
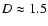 ,
,
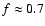 )
than brighter galaxies
(
)
than brighter galaxies
(
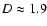 ,
,
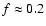 ).
).
Theoretically porosity is thought
to be crucial for the self-regulation of disks, and one expects an
increasing star-formation rate to be accompagnied with decreasing
porosity (Silk 1997, Eq. (7)). This holds empirically as well, as we
will sketch now. For dwarf irregular galaxies the area-normalized star
formation rate is correlated with the galaxy's extrapolated central
surface brightness: from Fig. 7a in van Zee (2001) we infer
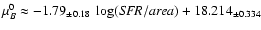 ,
with
,
with
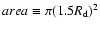 and
and 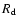 being the
exponential-model scale length in kpc. On the other hand, an ordinary
least-squares bisector fit (Isobe et al. 1990) to the data of
Fig. 7, right, yields
being the
exponential-model scale length in kpc. On the other hand, an ordinary
least-squares bisector fit (Isobe et al. 1990) to the data of
Fig. 7, right, yields
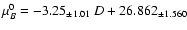 ,
shown as line in the figure. Equating the two expressions,
inserting Eq. (3), and remembering D=D3-1, we finally deduce
,
shown as line in the figure. Equating the two expressions,
inserting Eq. (3), and remembering D=D3-1, we finally deduce
![$\displaystyle SFR~[{M}_\odot ~{\rm yr}^{-1}] \approx
0.45~(1-f)^{1.8}~(R_{\rm d}~[{\rm kpc}])^2.$](/articles/aa/full/2003/05/aa3024/img79.gif) |
|
|
(4) |
Within our model treatment of dwarf irregular galaxies being
self-similar objects we thus have semi-empirically established a statistical relation between SFR, scale length, and porosity, in the
sense that for a given scale length galaxies with higher SFRs are also
less porous. Note that for a given scale length, Eq. (4) predicts
a maximum SFR. However, porosity as defined above has to be
understood as a conceptual parameter and not as a quantity describing
reality in detail. The parameters possibly influencing the mean
porosity of a galaxy are manyfold (gas density, gas pressure or
velocity dispersion, gas metallicity, supernova energy release),
forming an intricate, interdependent parameter set (Silk 1997; Oey &
Clarke 1997).


Up: Distribution of star-forming complexes
Copyright ESO 2003
![]() is assumed for the
cumulative number of points N(r) within a distance r around each
point. If the distribution is (at least partially) self-similar this
will be manifested in a
is assumed for the
cumulative number of points N(r) within a distance r around each
point. If the distribution is (at least partially) self-similar this
will be manifested in a ![]() -
-![]() diagram as a straight line
with slope D, called the cluster (or correlation) dimension,
diagram as a straight line
with slope D, called the cluster (or correlation) dimension,
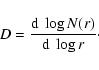
![]() and a
scatter of only about 0.1, these areas show relatively high cluster
dimensions that are typically lying above their galaxies'
values. It furthermore implies that cluster dimensions for local
lump aggregates scatter less than those for entire galaxies.
and a
scatter of only about 0.1, these areas show relatively high cluster
dimensions that are typically lying above their galaxies'
values. It furthermore implies that cluster dimensions for local
lump aggregates scatter less than those for entire galaxies.
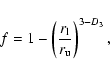
![]() ,
with
,
with
![]() and
and ![]() being the
exponential-model scale length in kpc. On the other hand, an ordinary
least-squares bisector fit (Isobe et al. 1990) to the data of
Fig. 7, right, yields
being the
exponential-model scale length in kpc. On the other hand, an ordinary
least-squares bisector fit (Isobe et al. 1990) to the data of
Fig. 7, right, yields
![]() ,
shown as line in the figure. Equating the two expressions,
inserting Eq. (3), and remembering D=D3-1, we finally deduce
,
shown as line in the figure. Equating the two expressions,
inserting Eq. (3), and remembering D=D3-1, we finally deduce