Suppose that for star i of N stars in total, there are M class W data,
with ![]() .
Let the weight for datum Fj be given by
.
Let the weight for datum Fj be given by
| wj = (Vw + vj)-1 | (B.1) |
(see Eq. (10.16) of Kendall & Stuart 1977). In this
equation, vj is a variance produced by EW error, while Vw is a
"frame-to-frame variance'' for which an initial guess is made. The calculated
values of wj are used to obtain a weighted average FM of the values of
Fj. A statistic Q is then calculated:
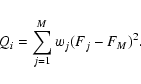 |
(B.2) |
Q is ![]() distributed with
distributed with
![]() degrees of freedom
(see Lampton et al. 1976, Appendix, Sect. III).
degrees of freedom
(see Lampton et al. 1976, Appendix, Sect. III). ![]() is the
associated number of degrees of freedom.
is the
associated number of degrees of freedom.
The values of Qi and ![]() are summed over the data for all N stars.
This procedure is repeated with a number of trial values of Vw. The correct
value of Vw is the one for which
are summed over the data for all N stars.
This procedure is repeated with a number of trial values of Vw. The correct
value of Vw is the one for which
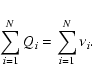 |
(B.3) |
The ![]() distribution may be used to calculate an rms error UW
for Vw. An equivalent number of degrees of freedom
distribution may be used to calculate an rms error UW
for Vw. An equivalent number of degrees of freedom ![]() is then obtained
from the following definition:
is then obtained
from the following definition:
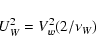 |
(B.4) |
(see Eq. (A.4) of T94).
As Eq. (B.1) shows, this algorithm requires knowledge of values of vj.
Those variances are calculated as follows:
| vj = vj0 nj-1, | (B.5) |
with nj being the number of contributing lines. Values of vj0 are sometimes given in contributing papers, but a default value of (0.072 dex)2 (from Favata et al. 1997) is commonly used instead. The results of the calculation are not at all sensitive to this choice because V is substantially larger than vj in almost all cases.
Copyright ESO 2003