Contents

• Chemical compositions of four barium stars
• 1 Introduction
• 2 Observations and data reduction
• 3 Stellar atmospheric parameters
• 4 Model atmospheres and spectral lines
• 5 Abundances and their uncertainties
• 6 Comparison with wind accretion model results
• 7 Discussions
• 8 Summary
• References
• Online Material

A&A 397, 257-265 (2003)
DOI: 10.1051/0004-6361:22021460

Chemical compositions of four barium stars

Y. C. Liang^1,2 - G. Zhao¹ - Y. Q. Chen¹ - H. M. Qiu¹ - B. Zhang^3,4

1 - National Astronomical Observatories, Chinese Academy of Sciences, 100012, Beijing, PR China
2 - GEPI, Observatoire de Paris-Meudon, 92195 Meudon, France
3 - Department of Physics, Hebei Normal University, 050016, Shijiazhuang, PR China
4 - Chinese Academy of Sciences-Peking University Joint Beijing Astrophysical Center, Beijing 100871, PR China

Received 26 August 2002 / Accepted 30 September 2002

Abstract
We obtain abundances of $\alpha$, iron peak and neutron capture (n-capture) process elements in four Ba stars HD 26886, HD 27271, HD 50082 and HD 98839 based on high resolution, high signal-to-noise spectra. We find that all of these Ba stars are disk stars. Their $\alpha$ and iron peak elements are similar to the solar abundances. The n-capture process elements are overabundant relative to the Sun. In particular, the second peak slow neutron capture process (s-process) elements, Ba and La, are higher than the first peak s-process elements, Y and Zr. Analyzing the abundances of four sample stars, the heavy-element abundances of the strong Ba star HD 50082 are higher than those of other three mild Ba stars. The stellar mass of the strong Ba star HD 50082 is 1.32 $M_{\odot}$ (+0.28, $-0.22~M_{\odot}$), which is consistent with the average mass of strong Ba stars (1.5 $M_{\odot}$). For mild Ba star HD 27271, we derive 1.90 $M_{\odot}$ (+0.25, $-0.20~M_{\odot}$), consistent with the average mass of mild Ba stars (1.9 $M_{\odot}$, with 0.6 $M_{\odot}$ white dwarf companion). For mild Ba star HD 26886, the derived 2.78 $M_{\odot}$ (+0.75, $-0.78~M_{\odot}$) is consistent with the average 2.3 $M_{\odot}$ of mild Ba stars with 0.67 $M_{\odot}$ companion white dwarfs within the errors. Mass of mild Ba star HD 98839 is high to 3.62 $M_{\odot}$, which inspires more thoughts on the formation of Ba star phenomenon. Using our angular momentum conservation theoretical model of wind accretion of Ba binary systems, we obtain the theoretical heavy-element abundances of Ba stars that best fit our data. The results show that the observed abundances of the typical strong Ba star HD 50082 and the typical mild Ba star HD 27271 are consistent with the theoretical results very well. This suggests that their heavy-element abundances were caused by accreting the ejecta of AGB stars, the progenitors of the present white dwarf companions, through stellar wind. However, wind accretion scenario cannot explain the observed abundance pattern of the mild Ba star HD 26886 with shorter orbital period (P= 1263.2 d). The mild Ba star HD 98839 with high mass (up to 3.62 $M_{\odot}$) and very long orbital period (P> 11 000 d) may be either a star with the heavy elements enriched by itself or a "true Ba" star.

Key words: stars: abundances - stars: atmospheres - stars: chemically peculiar - stars: evolution - stars: binaries: spectroscopic

1 Introduction

The "barium stars", or "Ba II stars" as they were first called, were defined as a class of peculiar red giants by Bidelman & Keenan (1951). These G and K giants exhibit enhanced features of Ba II, Sr II, CH, CN, and sometimes C₂ lines. Many qualitative studies on Ba II stars have been developed (e.g. Garstang 1952; Burbidge & Burbidge 1957; Danziger 1965; Pilachowski 1977; Tomkin & Lambert 1983; Smith 1984; Kovacs 1985; Za $\check{\rm c}$s 1994). The results confirmed that, in addition to Ba and Sr, other heavy elements are also enhanced, e.g. Y, Zr, La, Ce, Pr, Nd and Sm.

Some researchers suggested that the overabundances of Ba stars were produced in the interior of the Ba II star, and subsequently mixed to the surface (e.g. Burbidge & Burbidge 1957 for HD 46407). However, the absence of the unstable nucleus ⁹⁹Tc ( $\tau_{1 \over 2}=2\times 10^5$ yrs) supply evidence that they are not presently undergoing nucleosynthesis activity and the third dredge-up process like asymptotic giant branch (AGB) stars.

After Burbidge et al. (1957) suggested that elements heavier than iron are synthesized in the interior of AGB stars, it is generally believed that Ba stars belong to binary systems and their heavy-element overabundances are produced by accreting the matter ejected by the companions (the former AGB stars, now evolved into white dwarfs). Many researchers have studied the binarity or heavy-element abundances of Ba stars (McClure et al. 1980; McClure 1983; McClure & Woodsworth 1990; Boffin & Jorissen 1988; Jorissen & Mayor 1992; Jorissen et al. 1998; Liang et al. 2000). The mass exchange took place about $1\times 10^6$ years ago, so the ⁹⁹Tc produced in the original thermal pulse (TP) AGB stars have decayed. The accretion may be in the forms of wind accretion, disk accretion or common envelope ejection (Han et al. 1995; Jorissen et al. 1998; Liang et al. 2000).

Therefore, it is very important to combine abundance analysis and binary characters of Ba stars to study their properties and formation scenarios.

At present, there is a large sample of Ba stars with measurements of orbital elements (Carquillat et al. 1998; Udry et al. 1998a, 1998b; Jorissen et al. 1998), absolute magnitudes and kinematics (Gómez et al. 1997; Mennessier et al. 1997). However, the corresponding heavy-element abundances have not been obtained from observations. To explore their formation scenario, it is necessary to study their observed abundances, combined with their orbital elements.

Moreover, using our angular momentum conservation model of wind accretion of Ba stars formation, and combining the AGB stars nucleosynthesis (Liang et al. 2000; Liu et al. 2000), we can calculate the theoretical heavy-element abundances of Ba stars. Thus we can understand the observed abundance patterns of the sample stars from theory.

In addition, with the high precision Hipparcos data, the precise photometric parameters, improved methods to determine stellar atmospheric parameters and developed stellar evolutionary tracks study, it is possible to allow to obtain the masses and atmospheric parameters of these stars. For Ba stars, combining masses, element abundances and orbital parameters provides a good understanding of their properties and formation. In this paper, we discuss the properties of four Ba stars by combining these parameters.

This paper is organized as follows. In Sects. 2-4, we describe the observations and analysis methods in details, and present the derived atmosphere parameters and masses. Detailed spectral lines analysis and equivalent widths (EWs) are also presented. In Sect. 5, we show the element abundance patterns and analyze the abundance uncertainties. In Sect. 6, we calculate the theoretical abundance trends of s-process elements in Ba stars, and compare them with the observed patterns of our sample stars. Detailed discussions are given in Sect. 7. In Sect. 8, we summarize this paper and describe possible future studies.

2 Observations and data reduction

The high resolution spectra of four barium stars were obtained with the Coudé Echelle Spectrograph and a 1024 $\times$ 1024 TeK CCD attached to the 2.16 m telescope at the National Astronomical Observatories (Xinglong, China) in 2001. The red arm of the spectrograph with a 31.6 grooves/mm grating was used. With a 0.5 mm slit, the resolving power is of the order of 40 000 in the middle focus camera system. The total wavelength coverage was 5800-9000 Å. The signal-to-noise (S/N) ratio is greater than 150 over the whole region. A detailed description of technical aspects of the spectrograph can be found in Zhao & Li (2001).

The data reductions were carried out with a standard MIDAS package. The procedure is: order identification, background subtraction, flat-field correction, order extraction, wavelength calibration, radial velocity shift correction, and continuum normalization. Bias, dark current and scattered-light corrections are included in the background subtraction. The pixel-to-pixel sensitivity variations were corrected by using the flat-field. The wavelength calibration was based on thorium-argon lamp spectra. In Fig. 1, we present a portion of spectrum of the sample star HD 98839 in the region near Ba II $\lambda$6141.727 line.

Figure 1: Example of spectra of HD 98839: Ba II $\lambda$6141.727 line, Zr I $\lambda$6143.180 line and Si I $\lambda$6145.020 line.

The measurements of spectral line EWs were done by applying two different methods: direct integration of the line profile and Gaussian fitting. The latter is preferable in the case of faint lines, but unsuitable for the strong lines in which the damping wings contribute significantly to the equivalent width. The final EWs are weighted averages of these two measurements, depending on the line intensity (see Zhao et al. 2000 for details).

 

 

Table 1: Basic data of the sample stars.

Star name	Sp.	$V_{\rm mag}$	B-V	b-y	$\pi$	$\sigma_\pi$	BC	M/$M_{\odot}$
					(mas)
HD 26886	G5	7.00	0.92	0.596	2.74	1.05	-0.335	2.78(+0.75, -0.78)
HD 27271	G5	7.52	1.00	0.591	6.01	1.13	-0.306	1.90(+0.25, -0.20)
HD 50082	G0	7.43	1.03	0.611	4.71	0.99	-0.367	1.32(+0.28, -0.22)
HD 98839	G8II	4.99	0.98	0.610	6.63	0.63	-0.308	3.62(+0.45, -0.00)

3 Stellar atmospheric parameters

Model atmospheres are specified by four parameters: effective temperature, surface gravity, overall metallicity and microturbulent velocity.

Effective temperature $T_{\rm eff}$ is determined from the uvby system index (b-y) and [Fe/H] using the empirical calibration of Alonso et al. (1999). This calibration is based on a large sample of field and globular cluster stars roughly covering spectral type from F0 to K5, and derived by applying the infrared flux method. The photometric data of sample stars are taken from Olsen (1993) and Hauck & Mermilliod (1998). The error of the photometric data is $\sigma(b-y)=$ 0.004 mag. Adopting the mean $\sigma$(Fe/H) = 0.14 dex from the spectroscopic analysis, the statistical error of $T_{\rm eff}$ is estimated to about $\pm$50 K. Considering a possible error of $\pm$80 K in the calibration, and other factors, we estimate the error in $T_{\rm eff}$ as high as 100 K for our sample stars.

The previous method to determine gravity log g requires that Fe I and Fe II lines give the same iron abundance. But it is well known that the derivation of iron abundance from Fe I and Fe II lines may be affected by many factors such as unreliable oscillator strengths, possible non local  thermodynamic  equilibrium (non-LTE) effects and uncertainties in the temperature structure of the model atmospheres. From Hipparcos parallaxes, we can determine more reliable gravities. Using the relations:

$$\begin{eqnarray*}{\rm log} {g \over g_{\odot}}={\rm log} {M\over M_{\odot}} +4{\... ...}\over T_{{\rm eff},\odot}}+0.4(M_{\rm bol}-M_{{\rm bol},\odot}) \end{eqnarray*}$$

and

$$\begin{eqnarray*}M_{\rm bol}=V+5+5{\rm log} \pi +BC, \end{eqnarray*}$$

where M is the stellar mass, $M_{\rm bol}$ the absolute bolometric magnitude, Vthe visual magnitude, BC the bolometric correction, and $\pi$ the parallax. We adopt solar value log $g_\odot=$ 4.44, $T_{{\rm eff},\odot}=$ 5770 K, $M_{{\rm bol},\odot}=$ 4.75 mag. The parallax $\pi$ is taken from the Hipparcos Satellite observations (ESA 1997). Stellar mass was determined from the position of the star in $M_{\rm bol}-$log  $T_{\rm eff}$diagram. The corresponding errors were estimated by changing $T_{\rm eff}$, [Fe/H] and  $M_{\rm bol}$ according to its derivations (more details can be found in Chen et al. 2000). We adopt the stellar evolution tracks given by Girardi et al. (2000). The bolometric correction, BC, is determined using the empirical calibration of Alonso et al. (1999). The uncertainty of log g determined by this method mainly comes from the uncertainties in the stellar distance, stellar mass, effective temperature and bolometric correction. We estimate the error in log g to be in the range of 0.1-0.3 dex for our sample stars (Table 2 and the Col. 4 in Table 5).

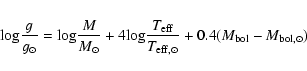
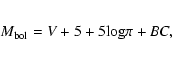
The initial metallicities of the program stars were taken from the literature if available. Otherwise, we obtain an initial value by judging from the spectra and the color index. The final model metallicity is derived from consistency with the other parameters in the abundance calculation.

Microturbulent velocity $\xi _{\rm t}$was determined from the abundance analysis by requiring a zero slope of [Fe/H] vs. EWs. The values of the sample stars are given in Table 2. The error of  $\xi _{\rm t}$ is about 0.3 km s^-1.

Some characteristic parameters of four barium stars are presented in Table 1. The columns are: star name, spectral type, V magnitude, (B-V), (b-y), parallax $\pi$, uncertainty of parallax, bolometric correction and stellar mass. The atmospheric parameters of the sample stars are summarized in Table 2 including star name, effective temperature, surface gravity, microturbulent velocity and metallicity.

4 Model atmospheres and spectral lines

We adopt the model atmospheres generated by ATLAS9 code (Kurucz 1993) to do the abundance analysis: these are LTE, plane-parallel, line-blanketed models. Abundances are determined by using the input atmospheric parameters given in Table 2 and the measured EWs. We usually choose the lines with EWs = 20 $\sim$ 120 mÅ, because the weaker lines would increase random error and possibly some systematic overestimates, while the stronger lines are very sensitive to the microturbulence and damping. We use the updated oscillator strengths of spectrum lines taken from the NIST database (http://physics.nist.gov). But the log gf values of n-capture process elements are taken from the related references (e.g. Hannaford et al. 1982; Bi $\acute{\rm e}$mont et al. 1981; Weise & Martin 1980; Luck & Bond 1991; Bi $\acute{\rm e}$mont et al. 1982). All of the lines used in determining abundances are given in Table 3, including line and wavelength, excitation potential $\chi$, oscillator strengths log gf and EWs. For Ba II $\lambda$5853.688 line in HD 98839, we find its EW is 171 mÅ, which is much lower than 259 mÅ obtained by Fernández-Villacañas et al. (1990). The EW values of Ba II  $\lambda\lambda$6141.727, 6496.908 lines in this star are higher than 200 mÅ obtained in this study.

 

 

Table 2: Atmospheric parameters of the sample stars.

Star name	$T_{\rm eff}$	log g	$\xi _{\rm t}$	[Fe/H]
	(K)		(km s-1)
HD 26886	4802	2.22 $\pm$ 0.3	1.2	-0.28 $\pm$ 0.16
HD 27271	4874	2.98 $\pm$ 0.2	1.4	-0.06 $\pm$ 0.14
HD 50082	4730	2.50 $\pm$ 0.2	1.5	-0.40 $\pm$ 0.14
HD 98839	4866	2.33 $\pm$ 0.1	1.6	+0.16 $\pm$ 0.16

5 Abundances and their uncertainties

5.1 Abundance results

The final abundances log $\epsilon$ (in the usual scale logX(H) = 12.0) and the corresponding induced [X/Fe] values are presented in Table 4, where N refers to the line number used in calculation. The solar abundances are taken from Grevesse & Sauval (1998).

Figures 2-d show the detailed abundance results. The corresponding errors are taken from Col. 6, $\sigma_{{\rm tot}}$, in Table 5. Detailed analysis about errors is discussed in next section (Sect. 5.2).

 

 

Table 4: Element abundances in the usual scale logX(H) = 12.0 and in the notation [X/Fe] in the four Ba stars.

		HD 26886			HD 27271			HD 50082			HD 98839
$\rm {[Fe/H]}$		-0.28			-0.06			-0.40			+0.16
Ion	N	log $\epsilon$	[X/Fe]	N	log $\epsilon$	[X/Fe]	N	log $\epsilon$	[X/Fe]	N	log $\epsilon$	[X/Fe]
Fe I	46	7.23	--	26	7.45	--	29	7.11	--	27	7.67	--
Fe II	5	7.35	--	6	7.49	--	5	7.26	--	4	7.82	--
O I	1	8.91	+0.36	2	9.16	+0.39		--	--	2	9.14	+0.15
Na I	2	5.97	-0.08	1	6.43	+0.16	1	6.01	+0.08	1	6.78	+0.29
Mg I	1	7.48	+0.18	1	7.62	+0.10	1	6.92	-0.26	1	7.72	-0.02
Al I	3	6.21	+0.02	2	6.44	+0.03	1	6.22	+0.15	1	6.61	-0.02
Si I	6	7.49	+0.22	3	7.70	+0.21	2	7.69	+0.54	5	7.90	+0.19
Ca I	4	6.18	+0.10	4	6.29	-0.01	6	5.97	+0.01	3	6.53	+0.01
Sc II	2	2.82	-0.07	1	3.11	0.00	1	2.93	+0.16	1	3.23	-0.10
Ti I	6	4.47	-0.27	4	4.79	-0.17	4	4.48	-0.14	3	4.95	-0.23
V I	1	3.46	-0.26	2	3.61	-0.33	2	3.22	-0.38	1	3.92	-0.24
Cr I	1	5.52	+0.13	2	5.87	+0.26	2	5.43	+0.16	2	6.06	+0.23
Mn I	2	5.28	+0.17	1	5.35	+0.02	1	5.22	+0.23	1	5.77	+0.22
Ni I	14	5.94	-0.03	14	6.18	-0.01	5	5.75	-0.10	9	6.37	-0.04
Y I	1	1.91	-0.05	1	2.65	+0.47	1	2.30	+0.46		--	--
Zr I	2	2.42	+0.10	4	2.95	+0.41	4	2.80	+0.60		--	--
Ba II	2	2.59	+0.74	3	2.74	+0.67	3	2.87	+1.14	3	2.85	+0.56
La II	1	1.56	+0.67	1	1.92	+0.81	1	2.12	+1.35	1	1.73	+0.40
Eu II	1	0.49	+0.26	1	0.81	+0.36	1	0.74	+0.63	1	0.94	+0.27

5.2 Errors in resulting abundances

Uncertainties of the abundances mainly come from equivalent widths measurement, log gf values and stellar atmospheric parameters.

Figure 2a: Abundance pattern of HD26886. The error bars were taken from Col. 6 in Table 5(1).

Figure 2b: Abundance pattern of HD27271. The error bars were taken from Col. 6 in Table 5(2).

Figure 2c: Abundance pattern of HD50082. The error bars were taken from Col. 6 in Table 5(3).

Figure 2d: Abundance pattern of HD98839. The error bars were taken from Col. 6 in Table 5(4).

Uncertainties in the EWs are set essentially by the S/N and the resolution of the spectra. An expression for the intrinsic accuracy of an equivalent width is provided by Cayrel (1988). Applied to our spectra, having R= 40 000 and typical S/N of 150, we expect uncertainties in the EWs of about 2 mÅ. We also consider the errors obtained by measuring EWs of spectral lines several times in the total uncertainties. For an element represented by N lines, the error is decreased by a factor $\sqrt N$. Thus the errors in element abundances from EWs are calculated and illustrated on Col. 2 in Table 5, $\sigma_{EW}/\sqrt N$.

The errors caused by atmospheric parameters can be obtained through changing the parameters $T_{\rm eff}$, log g, $\xi _{\rm t}$ individually. Columns 3, 4, 5 in Table 5 show the effects on the derived abundances by changing +100 K in $T_{\rm eff}$, +0.3, +0.2 or +0.1 dex in log g, +0.3 km s^-1 in  $\xi _{\rm t}$.

Model metallicity uncertainties scarcely affect the element abundances, and they can be ignored.

The uncertainty in gf-values of the Fe I and Fe II lines is about 0.05 dex. For the elements up to Ni, the uncertainties are about 0.02-0.10 dex, and for the heavier elements, the errors are $\sim$0.20 dex (Smith et al. 1995; Lambert et al. 1996; Junqueira & Pereira 2001).

The combined abundance errors caused by the above-mentioned uncertainties in gf-values, EWs-values and stellar atmospheric parameters, are the total errors in abundances, which are given in the last columns in Table 5(1)-(4) by $\sigma_{{\rm tot}}$.

5.3 Abundance pattern analysis

Among the four sample stars, HD 98839 shows the highest metallicity with [Fe/H] = +0.16, which is slightly higher than solar metallicity. HD 50082 shows the lowest metallicity with [Fe/H] = -0.40. The other two stars ([Fe/H] is -0.06 for HD 27271 and -0.28 for HD 26886) are nearer to solar metallicity than HD 98839 and HD 50082. However, it is clear that all of them are disk stars.

The [$\alpha$/Fe] of sample stars are similar to solar. And it is clear that [$\alpha$/Fe] patterns are lower than those of the two halo Ba stars ([Fe/H] = -1.72, -1.43) studied by Junqueira & Pereira (2001). Their two halo Ba stars show the overabundant [$\alpha$/Fe] relative to solar. The reason is that massive stars produce these $\alpha$ elements, which have been ejected into interstellar medium with the Type II supernova explosion of the massive stars since the early stage of our Galaxy. Most of element Fe is produced through Type Ia supernova explosion, which occurs in the close binary system composed by the longer lifetime, intermediate- and low-mass stars (Timmes et al. 1995; Samland 1998; Liang et al. 2001). Thus, there is abundant element Fe in our Galaxy at its present stage. The [$\alpha$/Fe] patterns of our sample Ba stars also show that all of these four stars are disk stars. In addition, it should be noticed that the [O/Fe] values of our three samples will be increased by 0.14 when we use the recent solar O abundance log $\epsilon$(O) = 8.69 obtained by Allende Prieto et al. (2001) based on [O I] $\lambda$6300 forbidden line. That is, the [O/Fe] ratio in HD 26886, HD 27271 and HD 98839 are 0.50, 0.53 and 0.29, respectively. But this increase value is still smaller than the corresponding abundance errors in the three sample stars: 0.22, 0.18 and 0.21, respectively.

For Na and Al, these two odd elements, their abundances are similar to Mg abundance, because these nuclei are thought to be synthesized in the same process, namely, carbon burning in massive stars.

The iron group elements follow Fe closely though with some scatter. Generally, Cr and Mn are slightly overabundant, and Ti, V are slightly underabundant. Especially, Ni, the closest element to Fe, is very similar to the Fe abundance in the sample stars.

However, it is not clear whether the larger scatter of $\alpha$ elements and iron elements in HD 50082 is the natural results of its strong Ba property or not.

The most important results are the obvious overabundance of s-process elements (Z> 56), Y, Zr and Ba, La, Eu (two peaks), in all of the four Ba stars (without appropriate Y and Zr lines are used in HD 98839 due to spectral qualities). Especially, the second peak s-process elements, Ba and La, are in the highest abundances. The origin of the two peaks is the result of neutron magic number 50 and 82 nuclei on the path of s-process nucleosynthesis occurred in the interiors of AGB stars (Clayton et al. 1961; Seeger et al. 1965), the progenitor companions of these Ba stars. There may be a third peak on element Pb corresponding to the neutron magic number 126. But it needs high quality blue spectra to get the Pb I $\lambda$$\lambda$3683, 4057 lines to obtain the Pb abundance.

To further degree, in the three sample Ba stars, the first peak s-elements, Y and Zr, show lower abundances than the second peak s-elements Ba, La etc. This trend also was shown in some other Ba stars given by Za $\check{\rm c}$s (1994). This [hs/ls] > 0 trend ("hs" refers to the second peak elements, "ls" refers to the first peak elements) shows that the neutron exposures experienced in their AGB progenitor companions are strong enough to produce the more abundant "hs" elements than the "ls" elements. If we plot our Ba samples and the corresponding AGB progenitor companions in Fig. 1 of Liang et al. (2000), or Fig. 6 of Busso et al. (1995) ([ls/Fe] vs. [hs/ls]), these stars should be in the [hs/ls] > 0 regions in the two figures. Our theoretical calculations given in next section certify this point.

This discrepancy between the two peak elements may be caused by the different neutron exposures in the companion AGB stars. Namely, the higher neutron exposure in the interior of AGB stars benefits to the production of the heavier s-process elements (Liang et al. 2000; Busso et al. 1995).

Comparing the abundance patterns of the two "typical" Ba star HD 27271 and HD 50082, we notice that the differences between the two peak elements (Y, Zr and Ba, La) are higher in HD 50082 than in HD 27271. It may be that the companion AGB star of HD 50082 experiences stronger neutron exposure in s-process nucleosynthesis. As a result, the abundances of all of the s-process elements of HD 50082 are higher than those of HD 27271. Our theoretical calculations certify this analysis (see Sect. 6).

As for calling HD 50082 and HD 27271 as "typical" Ba stars, the main reason is their masses. According to the scale defined by Warner (1965), there are three mild Ba stars in our samples: HD 26886, HD 27271 and HD 98839, and one strong Ba star HD 50082. The average masses are 1.9 $M_{\odot}$ and 1.5 $M_{\odot}$ respectively for mild Ba stars and strong Ba stars (Jorissen et al. 1998). We obtain masses of 1.90 $M_{\odot}$ and 1.32 $M_{\odot}$ for HD 27271 and HD 50082 respectively, which are consistent with the mass judgments well.

HD 26886 and HD 98839 also show over-abundant Ba and La, but the abundances are lower than those of HD 50082 and HD 27271. The elements Y, Zr of HD 26886 are weakly over-abundant. These results can be understood basically by the weaker overabundances of heavy elements in their AGB progenitor companions, by the lower neutron exposures occurred in the AGB progenitors.

6 Comparison with wind accretion model results

What is the reason to cause the heavy-element overabundances of Ba stars? It is generally believed that the overabundances are caused by binary accretion, namely, Ba stars accret the ejected materials from their companions, the former AGB stars (the present white dwarfs), which synthesized these heavy elements by themselves and ejected the elements into interstellar medium through stellar wind (Liang et al. 2000 and references therein).

In our previous paper (Liang et al. 2000), we calculated the s-process nucleosynthesis of AGB star with 3 $M_{\odot}$ and solar metallicity. At the same time, we set up an angular momentum conservation model of wind accretion in binary systems. Using such model we calculated the heavy-element abundances of Ba stars, and successfully explained the observed abundances of some samples taken from Za$\check{c}$s (1994) and Busso et al. (1995).

We try to explain the abundance patterns of our sample stars using our theoretical method. The calculation of the heavy element abundances of Ba stars is made in two separate steps. Firstly, adopting the theory of s-process nucleosynthesis and the latest TP-AGB model (Straniero et al. 1995; Straniero et al. 1997; Gallino et al. 1998; Busso et al. 1999), we calculate the overabundances of the intrinsic AGB star at each ejection. Then, combining the accreting matter predicted by the model of wind accretion on successive occasions and mixing, we calculate the heavy-element overabundances of the barium star. The s-process nucleosynthesis scenario and the change equations of orbital semi-major axis A and eccentricity e, $\frac{\Delta A}{A}$ and  $\frac{e\Delta e}{1-e^2}$, were given in Liang et al. (2000) and Liu et al. (2000).

The standard case of wind accretion is: M_1,0= 3.0 $M_{\odot}$, M_2,0= 1.3 $M_{\odot}$, $v_{\rm ej}=$ 15 ${\rm ~km~s^{-1}}$ (M_1,0 is the main sequence mass of the intrinsic AGB star, the present white dwarf, in the binary system; M_2,0 is the corresponding mass of the present Ba star; $v_{\rm ej}$ is the wind velocity). The used accretion rate is 0.15 times of the Bondi-Hoyle's accretion rate (Liang et al. 2000; Boffin & Za$\check{c}$s 1994).

We try to explain the observed abundances of our three Ba stars, HD 50082, HD 27271 and HD 26886, from theoretical calculations. Notice that there is no eccentricity of HD 98839 was observed, so we do not calculate the theoretical abundances to fit its observations. In our calculations, we try to make the calculated orbital period P and eccentricity e match the observations of the samples. Table 6 lists the observed orbital elements and their Ba classes of the samples taken from Jorissen et al. (1998), and their masses obtained by us (also in Table 2).

 

 

Table 6: Masses and orbital elements of the sample stars.

Star name	M/$M_{\odot}$	P	e	Ba
		(days)		classes
HD 26886	2.78(+0.75, -0.78)	1263.2	0.39	mild
HD 27271	1.90(+0.25, -0.20)	1693.8	0.22	mild
HD 50082	1.32(+0.28, -0.22)	2896.0	0.19	strong
HD 98839	3.62(+0.45, -0.00)	>11000	--	mild

As the studies show, the Ba stars with orbital period P> 1600 days can be formed through wind accretion (Zhang et al. 1999; Liang et al. 2000; Liu et al. 2000). Jorissen et al. (1998) suggested the corresponding period is 1500 days. Possibly, the Ba stars with lower orbital period form through other scenarios: dynamically stable late case C mass transfer or common envelope ejection.

For our sample of Ba stars, the orbital periods of HD 50082 and HD 27271 are 2896 and 1693.8 days (>1600 days) respectively. Their masses are consistent with the average masses of typical strong Ba stars (1.5 $M_{\odot}$) and mild Ba stars (1.9 $M_{\odot}$) (see Sect. 5.3), so we calculate the theoretical abundances of Ba stars using the standard case of our wind accretion model to compare with the observed patterns. Figures 3, b show that the calculations (the solid lines) can fit observations very well within the errors. The variable "a" represents the times of the corresponding standard exposures in the ¹³C profile suggested by Gallino et al. (1998) (details can be found in Liang et al. 2000). In summary, the higher a value reflects the higher neutron exposure occurred in interiors of AGB progenitor companions.

Figures 3, b show that the required neutron exposure characteristic parameter a is higher for HD 50082, a= 2.6; while for HD 27271, a= 1.6 is adequate. This difference reflects the "strong" and "mild" Ba properties of each star.

For HD 26886, since its mass is 2.78 $M_{\odot}$ (though with large error), we adopt 2.5 $M_{\odot}$ as the initial mass of a Ba star for a binary system in our calculation, instead of 1.3 $M_{\odot}$ in the standard case. However, the fit failed (Fig. 3). Maybe this is due to the lower orbital period of HD 26886 (1263.2 days) than the lower limit of wind accretion scenario (1600 or 1500 days). Perhaps dynamically stable late case C mass transfer or common envelope ejection scenario is the formation source of HD 26886. However, more studies are needed to understand this suggestion.

Figure 3a: The fitting of the predicted to observed heavy-element abundances of barium star HD 50082 using our wind accretion model.

Figure 3b: The fitting of the predicted to observed heavy-element abundances of barium star HD 27271 using the wind accretion model.

Figure 3c: The fitting of the predicted to observed heavy-element abundances of barium star HD 26886 using the wind accretion model.

7 Discussions

7.1 Stellar masses and mild Ba stars, strong Ba stars

Adopting stellar evolution tracks given by Girardi et al. (2000) and some related parameters (see Sect. 3), we calculate the masses of the sample Ba stars (see Tables 1, 6). Their masses are consistent with the statistical and theoretical results. Table 9 of Jorissen et al. (1998) shows that the average mass of mild Ba stars is 1.9 $M_{\odot}$ with 0.60 $M_{\odot}$ companion white dwarfs. For HD 27271, a mild Ba star, its mass is 1.90 $M_{\odot}$, which fits the average 1.9 $M_{\odot}$ of mild Ba stars very well. As for HD 26886, the calculated 2.78 $M_{\odot}$ is consistent with the average 2.3 $M_{\odot}$ of mild Ba stars with 0.67 $M_{\odot}$ companion white dwarfs (Jorissen et al. 1998) within the errors. HD 98839 is discussed in next section.

For the strong Ba star HD 50082, we obtain a mass of 1.32 $M_{\odot}$, which is consistent with the average mass 1.5 $M_{\odot}$ of strong Ba stars with 0.60 $M_{\odot}$ companion white dwarfs given by Jorissen et al. (1998).

Besides the different masses between the strong and mild Ba stars, their abundance patterns are different too (Sect. 5.3). What causes the discrepancy of abundances in these two Ba groups? Jorissen et al. (1998) carefully discuss the possible reasons. Considering our results, we emphasize and analyze two possible reasons again here: (i) a lower mass for the barium star results in a smaller dilution of the accreting materials in envelope of the Ba star; (ii) the lower metallicity results in larger heavy-element overabundances in the AGB progenitor. Our results are consistent with these two points. The strong Ba star HD 50082 has the lowest mass and lowest metallicity in the four samples. Thus it shows the highest heavy-element overabundances.

7.2 Inspiration from HD 98839: a "false Ba" star?

For HD 98839, the atmosphere parameters, [Fe/H] and over-rich Ba abundance obtained by us are similar to those of other researchers (Pilachowski 1977; Fernández-Villacañas et al. 1990; Mishenina 1996). We estimate its mass to be 3.62 $M_{\odot}$. Its high mass and heavy-element overabundance pose some questions on Ba stars formation through binary accretion and also on nucleosynthesis scenario of AGB stars.

The mass of HD 98839 is 3.62 $M_{\odot}$, higher than the average masses of mild Ba stars (1.9 or 2.3 $M_{\odot}$, see Sect. 7.1). And there is also a discrepancy between this value and the suggestion of Han et al. (1995), in which the authors assigned masses of less than 3 $M_{\odot}$ for all Ba stars.

How can these results and discrepancies be understood? On one hand, this mild Ba star may have been classified erroneously as Ba star, namely it is "false Ba" star, and the real story is that it produced the overabundant heavy elements by itself. However, according to the derived parameters, $M_{\rm bol}= -$1.2 and $T_{\rm eff}=$ 4866 K, HD 98839 should not evolve to AGB stage. Generally, AGB stars have $M_{\rm bol}$ from -1.7 to -5.5 and  $T_{\rm eff}$ from 3200 K to 3850 K respectively (Smith & Lambert 1985, 1986, 1990). In this case, if the heavy element overabundances of HD 98839 is an intrinsic nucleosynthesis event within itself, the over-rich s-process elements is usually associated with mixing process at the helium core flare, which is consistent with the alternative origin for the Ba II star phenomenon suggested by Malaney (1987) and Malaney & Lambert (1988). Also, Mennessier et al. (1997) suggested that some of their mild Ba stars with mass higher than 3 $M_{\odot}$ may be lower luminosity, post He-flare stars.

Moreover, HD 98839 displays very long orbital period (>11000 days) up to the upper detected limit (Jorissen et al. 1998), and there is no observed binary orbital eccentricity. Thus, it is not unrealistic to consider it as an independent star.

However, if these high mass mild Ba stars are really "true Ba" stars, and the binary accretions cause their heavy element overabundances, it will challenge the present nucleosynthesis scenario of AGB stars. At present, the popular viewpoint is that 1-3 $M_{\odot}$ low mass AGB stars with ¹³C neutron source are the main nucleosynthesis sites of s-process elements, while the intermediate mass AGB stars with ²²Ne neutron source cannot fit to the observations (Malaney 1987; Busso et al. 1995; Busso et al. 1999; Liang et al. 2000). However, if masses of Ba stars are higher than 3 $M_{\odot}$, their companions should be intermediate mass stars on the main-sequence. How the intermediate mass AGB stars result in the heavy element overabundance of these Ba stars? If this is the case, what kind of neutron exposure scenario works? Single exposure? More studies are needed on s-process nucleosynthesis scenario of AGB stars. Certainly, we need also the large sample of high mass mild Ba stars to check its abundance patterns.

In addition to the high mass (3.62 $M_{\odot}$) of mild Ba star, HD 98839, obtained by us, there are also some other high mass samples. Smith et al. (1980) calculated mass of $\zeta$ Cap is about 3.5 $M_{\odot}$, but with large error (+3.6, -1.8 $M_{\odot}$) (also see Boffin & Jorissen 1988). Mennessier et al. (1997) studied higher mass Ba stars. They estimated that the masses are up to 7 $M_{\odot}$ for their group S and 4.5 $M_{\odot}$ for group C in which there are mild Ba stars. Monte Carlo simulations of Karakas et al. (2000) predict that the masses of Ba stars may be up to 6 $M_{\odot}$.

Therefore, it is necessary to pay more attention on these high mass mild Ba stars.

8 Summary

We obtain abundances of $\alpha$, iron peak and s-process elements in four Ba stars, HD 50082, HD 27271, HD 26886 and HD 98839, using high resolution and high S/N spectra. The results show that all of samples are disk stars. They show the similar metallicities and the similar abundances of $\alpha$-elments and iron peak elements to the solar values. All of them show s-process element overabundances relative the solar. We obtain their masses using the highly precise Hipparcos data, precise photometric parameters and stellar evolution tracks. The mass results fit well the average characteristic masses of strong and mild Ba stars. And the high mass of mild Ba star HD 98839 pose more thoughts on Ba star phenomenon.

Using our wind accretion model of binary systems and AGB stars s-element nucleosynthesis calculation, we conclude that the wind accretion formation scenario is possible for HD 50082 and HD 27271. Wind accretion cannot explain the observations of HD 26886 with the short orbital period (P< 1600 days). The mild Ba star HD 98839 with high mass and very long orbital period may be either a "false Ba" star with the heavy elements enriched by itself or a "true Ba" star.

Fortunately, though we only have four samples, they represent wide Ba star groups. From stellar masses, there is one strong Ba star among them, and also mild Ba stars; there are the members with typical mass of Ba stars, also there are the high mass mild Ba stars, which are controversial. From orbital elements, there are samples in typical wind accretion orbital period range, there is one sample with very long orbital period, up to the detected limit, and there is one sample with shorter value, which may correspond to other formation scenarios. So these samples are very interesting in understanding the abundance patterns and formation scenarios of Ba stars.

Certainly, we need larger samples to understand the nature of Ba stars. At present, there is a large sample of Ba stars with orbital elements (Carquillat et al. 1998; Udry et al. 1998a, 1998b; Jorissen et al. 1998), but without the corresponding element abundances. It is very interesting and necessary to obtain their element abundances to be combined with the orbital elements. It is specially important to compare the related results of the two groups with different orbital periods: P< 1600 and P> 1600 days, and to study the stars with very long orbital periods. These results will help us to understand the various formation scenarios of Ba stars. At the same time, it is important to obtain their masses, particularly, for the possible high mass mild Ba stars. Maybe these high mass mild Ba stars can give more clues on AGB stars nucleosynthesis. Moreover, it will be helpful to understand the different abundance patterns between "strong" and "mild" Ba stars.

There is a larger sample of Ba stars (318 from L $\ddot{\rm u}$ catalogue 1991) have been studied whose absolute magnitudes and kinematics by Gómez et al. (1997). Their results show that the sample of Ba stars are an inhomogeneous group, three of them among the four groups are disk population stars, and the fourth group contains halo stars. Mennessier et al. (1997) confirmed further this inhomogenity. If we can supplement the heavy-element abundances to compare the various characters of these different groups, it will be a stronger method to understand the natural properties of Ba stars.

In addition, it is better to obtain the carbon and oxygen abundances together with s-process elements. The reason is that AGB stars are important nucleosynthesis sources of element carbon, which is taken out from stellar interiors together with s-process elements by the third dredge-up process (Liang et al. 2000; Liang et al. 2001). Element carbon will be then accreted by Ba stars, the companions of binary systems.

Considering Ba stars from stellar population, it is interesting to combine Ba stars with CH stars. Some reseachers suggest that metal-rich stars evolve into Ba stars and the metal-poor stars evolve to CH stars, which are metal-poor stars (Vanture 1992a,b). At present, it is believable that nucleosynthesis of metal-poor AGB stars are more efficient than the metal-rich one (Busso et al. 1999; Busso et al. 2001). Thus, it is valuable to study the heavy-element abundances of metal-poor CH stars. But CH stars are fainter, some are as low as 12 mag, which makes more difficult to get the required spectra.

CH subgiants (Luck & Bond 1982, 1991; Smith et al. 1993), Ba dwarfs (North et al. 1994) and extrinsic S stars (Jorissen et al. 1998) should be the closest groups to Ba giants. It will be interesting to combine and compare all of these group stars. Perhaps we will then be able to study Ba stars in an evolutionary sequence.

Acknowledgements

We thank the anonymous referee for very useful suggestions on the original manuscript. We thank Dr. Rafael Guzmán for his great help for improving the English expression. Y. C. Liang thanks Dr. Francois Hammer and other staffs of GEPI for their friendly help. Y. C. Liang thanks Huawei Zhang, Jianrong Shi, Zhenxi Zhu, Guangshun Bai and Gang Liu for their help with data reduction. This research work is supported by the National Natural Science Foundation of China under grant No. 10173014 and NKBRSF G1999075406.

References

 
• Allende Prieto, C., Lambert, D. L., & Asplund, M. 2001, ApJ, 556, L63 NASA ADS  
• Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&AS, 140, 261 NASA ADS  
• Bidelman, W. K., & Keenan, P. C. 1951, ApJ, 114, 473 NASA ADS  
• Bi$\acute{\rm e}$mont, E., Grevesse, N., Hannaford, P., et al. 1981, ApJ, 248, 867 NASA ADS  
• Bi$\acute{\rm e}$mont, E., Karner, C., Meyer, G., et al. 1982, A&A, 107, 166 NASA ADS  
• Boffin, H. M. J., & Jorissen, A. 1988, A&A, 205, 155 NASA ADS  
• Boffin, H. M. J., & Za$\check{\rm c}$s, L. 1994, A&A, 291, 811 NASA ADS  
• Burbidge, E. M., & Burbidge, G. R. 1957, ApJ, 126, 357 NASA ADS  
• Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 NASA ADS  
• Busso, M., Lambert, D. L., Beglio, L., et al. 1995, ApJ, 446, 775 NASA ADS  
• Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 NASA ADS  
• Busso, M., Gallino, R., Lambert, D. L., Travaglio, C., & Smith, V. V. 2001, ApJ, 557, 802 NASA ADS  
• Carquillat, J. M., Jorissen, A., Udry, S., & Ginestet, N. 1998, A&AS, 131, 49 NASA ADS  
• Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, ed. G. Cayrel de Strobel, & M. Spite (Kluwer, Dordrecht), IAU Symp., 132, 345  
• Chen, Y. Q., Nissen, P. E., Zhao, G., et al. 2000, A&AS, 141, 491 NASA ADS  
• Clayton, D. D., Fowler, W. A., Hull, T. E., et al. 1961, Ann. Phys., 12, 331  
• Danziger, I. J. 1965, MNRAS, 131, 51 NASA ADS  
• ESA 1997, the Hipparcos and Tycho Catalogues, ESA SP-1200  
• Fernández-Villacañas, J. I., Rego, M., & Cornts, M. 1990, AJ, 99, 1961 NASA ADS  
• Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 NASA ADS  
• Garstang, R. H. 1952, PASP, 64, 227 NASA ADS  
• Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 NASA ADS  
• G$\acute{\rm o}$mez, A. E., Luri, X., Grenier, S., et al. 1997, A&A, 319, 881 NASA ADS  
• Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 NASA ADS  
• Han, Z., Eggleton, P., Podsiadlowski, P., & Tout, C. A. 1995, MNRAS, 277, 1443 NASA ADS  
• Hannaford, P., Lowe, R. M., Grevesse, N., et al. 1982, ApJ, 261, 736 NASA ADS  
• Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 NASA ADS  
• Jorissen, A., & Mayor, M. 1992, A&A, 260, 115 NASA ADS  
• Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877  
• Junqueira, S., & Pereira, C. B. 2001, AJ, 122, 360 NASA ADS  
• Karakas, A. I., Tout, C. A., & Lattanzio, J. C. 2000, MNRAS, 316, 689 NASA ADS  
• Kovacs, N. 1985, A&A, 150, 232 NASA ADS  
• Kurucz, R. L. 1993, CD-ROM, vol. 13, Smithsonian Astrophysics Observatory (Cambridge)  
• Lambert, D. L., Heath, J. E., Lemke, M., et al. 1996, ApJS, 103, 183 NASA ADS  
• Liang, Y. C., Zhao, G., & Zhang, B. 2000, A&A, 363, 555 NASA ADS  
• Liang, Y. C., Zhao, G., & Shi, J. R. 2001, A&A, 374, 936 NASA ADS  
• Liu, J. H., Zhang, B., & Liang, Y. C. 2000, A&A, 363, 660 NASA ADS  
• L$\ddot{\rm u}$, P. K. 1991, AJ, 101, 2229 NASA ADS  
• Luck, R. E., & Bond, H. E. 1982, ApJ, 259, 792 NASA ADS  
• Luck, R. E., & Bond, H. E. 1991, ApJS, 77, 515 NASA ADS  
• Malaney, R. A. 1987, ApJ, 321, 832 NASA ADS  
• Malaney, R. A., & Lambert, D. L. 1988, MNRAS, 235, 695 NASA ADS  
• McClure, R. D., Fletcher, J. M., & Nemec, J. M. 1980, ApJ, 238, L35 NASA ADS  
• McClure, R. D. 1983, ApJ, 268, 264 NASA ADS  
• McClure, R. D., & Woodsworth, A. W. 1990, ApJ, 352, 709 NASA ADS  
• Mennessier, M. O., Luri, X., Figueras, F., et al. 1997, A&A, 326, 722 NASA ADS  
• Mishenina, T. V. 1996, A&AS, 119, 321 NASA ADS  
• NIST http://physics.nist.gov  
• North, P., Berthet, S., & Lanz, T. 1994, A&A, 281, 775 NASA ADS  
• Olsen, E. H. 1993, A&AS, 102, 89 NASA ADS  
• Pilachowski, C. A. 1977, A&A, 54, 465 NASA ADS  
• Samland, M. 1998, ApJ, 496, 155 NASA ADS  
• Seeger, P. A., Fowler, W. A., & Clayton, D. D. 1965, ApJS, 11, 121 NASA ADS  
• Smith, V. V. 1984, A&A, 132, 326 NASA ADS  
• Smith, V. V., Coleman, H., & Lambert, D. L. 1993, ApJ, 417, 287 NASA ADS  
• Smith, V. V., Cunha, K., & Lambert, D. L. 1995, AJ, 110, 2827 NASA ADS  
• Smith, V. V., & Lambert, D. L. 1985, ApJ, 294, 326 NASA ADS  
• Smith, V. V., & Lambert, D. L. 1986, ApJ, 311, 843 NASA ADS  
• Smith, V. V., & Lambert, D. L. 1990, ApJS, 72, 387 NASA ADS  
• Smith, V. V., Sneden, C., & Pilachowski, C. A. 1980, PASP, 92, 809 NASA ADS  
• Straniero, O., Chieffi, A., Limongi, M., et al. 1997, ApJ, 478, 332 NASA ADS  
• Straniero, O., Gallino, R., Busso, M., et al. 1995, ApJ, 440, L85 NASA ADS  
• Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 NASA ADS  
• Tomkin, J., & Lambert, D. L. 1983, ApJ, 273, 722 NASA ADS  
• Udry, S., Jorissen, A., Mayor, M., & Van Eck, S. 1998a, A&AS, 131, 25 NASA ADS  
• Udry, S., Mayor, M., Van Eck, S., et al. 1998b, A&AS, 131, 43 NASA ADS  
• Vanture, A. D. 1992a, AJ, 104, 1986 NASA ADS  
• Vanture, A. D. 1992b, AJ, 104, 1997 NASA ADS  
• Warner, B. 1965, MNRAS, 129, 263 NASA ADS  
• Weise, W. L., & Martin, G. A. 1980, NSDRS-NBS, 68  
• Za$\check{\rm c}$s, L. 1994, A&A, 283, 937 NASA ADS  
• Zhang, B., Liu, J.-h., Liang, Y.-c., & Peng, Q.-h. 1999, Chin. Astron. Astrophys., 23, 189 NASA ADS  
• Zhao, G., & Li, H. B. 2001, ChJAA, 1, 555 NASA ADS  
• Zhao, G., Qiu, H. M., Chen, Y. Q., & Li, Z. W. 2000, ApJS, 126, 461 NASA ADS

 

Online Material

   

Table 3: Observed ion lines

					EWs (mÅ)
$\lambda$(Å)	Ion	$\chi$ (eV)	log gf	Ref.*	HD 26886	HD 27271	HD 50082	HD 98839
5806.732	Fe I	4.61	-1.05		70	77	--	--
5809.224	Fe I	3.88	-1.84		76	--	--	--
5856.096	Fe I	4.29	-1.33		52	--	61	76
5859.596	Fe I	4.55	-0.66		--	--	81	--
5862.368	Fe I	4.55	-0.45		99	--	--	--
5905.680	Fe I	4.65	-0.73		--	83	70	--
5916.257	Fe I	2.45	-2.99		94	--	102	--
5927.797	Fe I	4.65	-1.09		54	59	47	76
5929.682	Fe I	4.55	-1.41		--	64	--	85
5930.191	Fe I	4.65	-0.23		99	112	97	--
5934.665	Fe I	3.93	-1.17		97	--	--	--
5956.706	Fe I	0.86	-4.50		104	--	--	--
6003.022	Fe I	3.88	-1.12		106	113	104	--
6027.059	Fe I	4.07	-1.09		86	94	93	120
6056.013	Fe I	4.73	-0.46		81	90	88	114
6079.016	Fe I	4.65	-1.12		--	72	--	--
6093.649	Fe I	4.61	-1.50		36	50	41	62
6096.671	Fe I	3.98	-1.93		55	59	--	79
6151.623	Fe I	2.18	-3.28		81	--	90	116
6165.363	Fe I	4.14	-1.47		65	--	69	--
6173.341	Fe I	2.22	-2.88		109	119	116	--
6180.209	Fe I	2.73	-2.58		88	113	--	--
6187.995	Fe I	3.94	-1.72		--	61	70	93
6200.321	Fe I	2.61	-2.44		--	118	114	--
6215.149	Fe I	4.19	-1.13		109	--	--	--
6229.232	Fe I	2.84	-2.81		66	--	--	108
6232.648	Fe I	3.65	-1.22		112	--	--	--
6240.653	Fe I	2.22	-3.27		90	--	--	--
6322.694	Fe I	2.59	-2.45		--	--	115	--
6336.830	Fe I	3.69	-0.86		122	--	--	--
6380.750	Fe I	4.19	-1.29		77	--	82	112
6481.878	Fe I	2.28	-2.97		102	119	110	--
6518.373	Fe I	2.83	-2.45		--	103	--	--
6597.561	Fe I	4.80	-1.06		53	--	--	74
6609.118	Fe I	2.56	-2.66		99	--	113	--
6703.576	Fe I	2.76	-3.16		74	83	74	113
6726.673	Fe I	4.61	-1.00		60	--	--	--
6733.151	Fe I	4.64	-1.58		41	--	--	60
6750.164	Fe I	2.42	-2.60		104	--	111	--
6752.716	Fe I	4.64	-1.20		50	--	--	--
6806.856	Fe I	2.73	-3.21		66	75	68	99
6810.267	Fe I	4.61	-0.99		62	72	--	89
6828.596	Fe I	4.64	-0.92		74	88	--	106
6839.835	Fe I	2.56	-3.45		--	--	70	105
6842.689	Fe I	4.64	-1.32		--	--	44	--
6843.655	Fe I	4.55	-0.93		79	--	78	113
6858.155	Fe I	4.61	-0.93		--	83	--	--
7071.866	Fe I	4.61	-1.70		36	47	37	53
7112.170	Fe I	2.99	-2.99		61	--	68	--
7132.985	Fe I	4.07	-1.63		60	--	--	98
7219.680	Fe I	4.07	-1.35		65	71	--	90
7306.570	Fe I	4.18	-1.74		57	--	--	--
7418.672	Fe I	4.14	-1.38		67	--	73	108
7583.796	Fe I	3.02	-1.88		120	--	--	--
7723.210	Fe I	2.28	-3.62		73	--	--	112
8365.640	Fe I	3.25	-2.04		--	--	115	--
8515.122	Fe I	3.02	-2.07		111	--	--	--
8598.836	Fe I	4.39	-1.09		--	90	--	--
8699.461	Fe I	4.95	-0.38		75	89	--	100
5991.378	Fe II	3.15	-3.56		--	52	47	79
6149.249	Fe II	3.89	-2.72		52	--	50	--
6247.562	Fe II	3.89	-2.26		70	70	65	99

 

Table 3: Continued

				EWs (mÅ)
$\lambda$(Å)	Ion	$\chi$ (eV)	log gf	Ref.*	HD 26886	HD 27271	HD 50082	HD 98839
6416.928	Fe II	3.89	-2.74		49	53	47	78
6432.683	Fe II	2.89	-3.58		--	55	61	--
6456.391	Fe II	3.90	-2.07		95	78	--	--
6516.083	Fe II	2.89	-3.10		88	--	--	110
7711.731	Fe II	3.90	-2.47		--	58	--	--
7771.954	O I	9.14	0.33		52	51	--	64
7774.177	O I	9.14	0.19		--	56	--	65
6154.230	Na I	2.10	-1.57		50	80	57	107
6160.753	Na I	2.10	-1.23		72	--	--	--
8717.833	Mg I	9.53	-0.97		77	97	40	100
6698.670	Al I	3.14	-1.87		38	--	37	--
7835.317	Al I	4.02	-0.58		46	70	--	83
7836.130	Al I	4.02	-0.40		62	85	--	--
5948.548	Si I	5.08	-1.19		94	110	--	124
6125.026	Si I	5.61	-1.54		40	57	53	59
6142.494	Si I	5.62	-1.48		43	--	--	--
6145.020	Si I	5.62	-1.43		--	--	--	78
7405.790	Si I	5.61	-0.68		100	90	--	139
7415.958	Si I	5.61	-0.71		--	--	111	--
7800.000	Si I	6.18	-0.78		58	--	--	--
7932.351	Si I	5.96	-0.35		95	--	--	116
5867.572	Ca I	2.93	-1.61		--	--	36	--
6161.295	Ca I	2.52	-1.19		98	--	--	--
6166.440	Ca I	2.52	-1.19		94	104	104	120
6169.044	Ca I	2.52	-0.80		108	132	--	156
6455.605	Ca I	2.52	-1.29		--	97	83	--
6471.668	Ca I	2.52	-0.69		121	139	127	150
6245.620	Sc II	1.51	-0.98		77	--	--	--
6604.600	Sc II	1.36	-1.16		71	--	83	97
5866.461	Ti I	1.07	-0.84		91	--	--	132
5953.170	Ti I	1.89	-0.20		--	83	--	--
6126.224	Ti I	1.07	-1.32		61	--	87	86
6258.110	Ti I	1.44	-0.43		88	--	--	--
6261.106	Ti I	1.43	-0.48		86	106	93	--
6312.241	Ti I	1.46	-1.55		20	30	--	--
6599.110	Ti I	0.90	-2.08		--	47	42	55
6743.120	Ti I	0.90	-1.63		49	--	58	--
6090.216	V I	1.08	-0.14		68	87	78	101
6216.358	V I	0.28	-0.75		--	91	84	--
6979.806	Cr I	3.46	-0.41		--	81	63	94
7400.188	Cr I	2.90	-0.17		104	128	108	149
6013.497	Mn I	3.07	-0.15		113	--	--	--
6021.803	Mn I	3.07	0.01		116	132	134	161
6086.288	Ni I	4.26	-0.53		60	63	--	79
6108.125	Ni I	1.68	-2.62		106	116	--	--
6111.078	Ni I	4.09	-0.81		46	60	--	69
6128.984	Ni I	1.68	-3.33		57	--	65	93
6130.141	Ni I	4.26	-0.96		--	43	26	--
6176.816	Ni I	4.09	-0.26		82	82	--	--
6322.169	Ni I	4.15	-1.17		--	35	--	--
6327.604	Ni I	1.68	-3.11		--	91	89	111
6482.809	Ni I	1.93	-2.63		85	91	78	113
6586.319	Ni I	1.95	-2.73		72	92	--	112
6635.150	Ni I	4.42	-0.83		30	--	--	56
6767.784	Ni I	1.83	-2.17		118	--	--	--
6772.321	Ni I	3.66	-0.95		62	80	68	101
7385.244	Ni I	2.74	-1.97		--	--	--	110
7422.286	Ni I	3.63	-0.32		117	--	--	--
7715.591	Ni I	3.70	-0.95		74	88	--	--
7727.616	Ni I	3.68	-0.17		--	125	--	--
7748.894	Ni I	3.70	-0.33		114	126	--	--
7797.588	Ni I	3.90	-0.30		92	95	--	--

 

Table 3: Continued

					EWs (mÅ)
$\lambda$(Å)	Ion	$\chi$ (eV)	log gf	Ref.*	HD 26886	HD 27271	HD 50082	HD 98839
6435.000	Y I	0.07	-0.82	h	25	47	51	--
6127.460	Zr I	0.15	-1.06	b	--	44	49	--
6134.570	Zr I	0.00	-1.28	b	--	36	44	--
6140.460	Zr I	0.52	-1.41	b	5	16	17	--
6143.180	Zr I	0.07	-1.10	b	27	44	69	--
5853.688	Ba II	0.60	-1.01	wm	--	158	200	171
6141.727	Ba II	0.70	-0.08	wm	255	239	370	246
6496.908	Ba II	0.60	-0.38	wm	245	235	341	257
6390.480	La II	0.32	-1.45	lb	48	48	82	51
6645.110	Eu II	1.37	0.20	b2	30	28	41	45

$^{{\rm *}}$ References-- h: Hannaford et al. (1982); b: Bi$\acute{e}$mont et al. (1981); wm:
         Weise & Martin (1980); lb: Luck & Bond (1991); b2: Bi$\acute{e}$mont et al. (1982).

 

 

Table 5: (1): Abundances uncertainties of HD 26886.

		HD 26886
Ion	$\frac{\sigma_{EW}}{\sqrt N}$	$\Delta T_{\rm eff}$	$\Delta \log g$	$\Delta \xi_{\rm t}$	$\sigma_{{\rm tot}}$
		+100 K	+0.3	+0.3 km s-1
Fe I	0.02	0.08	0.01	-0.14	0.16
Fe II	0.07	-0.08	0.14	-0.14	0.22
O I	0.12	-0.15	0.11	-0.03	0.22
Na I	0.07	0.08	-0.01	-0.04	0.11
Mg I	0.10	0.03	-0.03	-0.04	0.11
Al I	0.05	0.08	-0.01	-0.03	0.10
SI I	0.05	-0.01	0.04	-0.06	0.09
Ca I	0.10	0.11	-0.03	-0.16	0.22
Sc II	0.10	-0.01	0.12	-0.11	0.19
TI I	0.05	0.15	-0.01	-0.10	0.19
V I	0.13	0.16	0.00	-0.09	0.22
Cr I	0.19	0.12	-0.02	-0.18	0.29
Mn I	0.15	0.12	-0.04	-0.20	0.28
NI I	0.04	0.06	0.03	-0.14	0.16
Y I	0.05	0.24	0.08	-0.02	0.27
Zr I	0.04	0.19	0.03	-0.01	0.21
Ba II	0.08	0.03	0.01	-0.07	0.14
La II	0.11	0.02	0.13	-0.09	0.21
Eu II	0.08	-0.01	0.13	-0.05	0.18

 

Table 5: (2): Abundances uncertainties of HD 27271.

		HD 27271
Ion	$\frac{\sigma_{EW}}{\sqrt N}$	$\Delta T_{\rm eff}$	$\Delta \log g$	$\Delta \xi_{\rm t}$	$\sigma_{{\rm tot}}$
		+100 K	+0.2	+0.3 km s-1
Fe I	0.03	0.05	0.01	-0.13	0.14
Fe II	0.07	-0.03	0.17	-0.03	0.19
O I	0.08	-0.14	0.07	-0.03	0.18
Na I	0.11	0.08	-0.02	-0.05	0.15
Mg I	0.09	0.03	-0.03	-0.03	0.11
Al I	0.07	0.05	-0.02	-0.04	0.11
Si I	0.07	-0.02	0.02	-0.07	0.10
Ca I	0.09	0.11	-0.03	-0.14	0.20
Sc II	0.13	-0.01	0.08	-0.11	0.19
Ti I	0.06	0.14	-0.00	-0.08	0.17
V I	0.10	0.16	0.00	-0.12	0.22
Cr I	0.11	0.10	-0.02	-0.13	0.20
Mn I	0.18	0.12	-0.04	-0.16	0.27
Ni I	0.04	0.04	-0.02	-0.11	0.12
Y I	0.07	0.21	0.02	-0.04	0.24
Zr I	0.04	0.19	0.01	-0.03	0.21
Ba II	0.09	0.03	0.01	-0.11	0.16
La II	0.10	0.02	0.09	-0.07	0.17
Eu II	0.07	-0.01	0.09	-0.04	0.13

 

Table 5: (3): Abundances uncertainties of HD 50082.

		HD 50082
Ion	$\frac{\sigma_{EW}}{\sqrt N}$	$\Delta T_{\rm eff}$	$\Delta \log g$	$\Delta \xi_{\rm t}$	$\sigma_{{\rm tot}}$
		+100 K	+0.2	+0.3 km s-1
Fe I	0.03	0.07	0.01	-0.12	0.14
Fe II	0.05	-0.09	0.10	-0.08	0.16
Na I	0.08	0.08	-0.01	-0.03	0.12
Mg I	0.06	0.02	0.00	-0.01	0.07
Al I	0.06	0.07	-0.00	-0.02	0.10
Si I	0.09	-0.02	0.03	-0.06	0.11
Ca I	0.06	0.10	-0.01	-0.10	0.15
Sc II	0.15	-0.01	0.08	-0.10	0.19
Ti I	0.06	0.16	0.00	-0.07	0.18
V I	0.09	0.16	0.01	-0.09	0.20
Cr I	0.10	0.10	-0.01	-0.12	0.18
Mn I	0.19	0.11	-0.04	-0.18	0.28
Ni I	0.05	0.06	0.04	-0.08	0.12
Y I	0.07	0.20	0.06	-0.04	0.23
Zr I	0.04	0.18	0.03	-0.03	0.21
Ba II	0.08	0.03	0.00	-0.07	0.14
La II	0.16	0.03	0.08	-0.16	0.26
Eu II	0.08	-0.01	0.09	-0.05	0.15

 

Table 5: (4): Abundances uncertainties of HD 98839.

		HD 98839
Ion	$\frac{\sigma_{EW}}{\sqrt N}$	$\Delta T_{\rm eff}$	$\Delta \log g$	$\Delta \xi_{\rm t}$	$\sigma_{{\rm tot}}$
		+100 K	+0.1	+0.3 km s-1
Fe I	0.03	0.06	0.01	-0.14	0.15
Fe II	0.09	-0.09	0.05	-0.15	0.20
O I	0.13	-0.16	0.04	-0.05	0.21
Na I	0.15	0.10	-0.11	-0.08	0.22
Mg I	0.11	0.03	-0.01	-0.05	0.13
Al I	0.11	0.05	-0.01	-0.05	0.13
Si I	0.07	-0.02	0.01	-0.09	0.11
Ca I	0.13	0.10	-0.01	-0.18	0.24
Sc II	0.16	-0.01	0.04	-0.12	0.20
Ti I	0.09	0.16	0.00	-0.11	0.21
V I	0.10	0.16	0.00	-0.13	0.23
Cr I	0.14	0.11	-0.00	-0.16	0.24
Mn I	0.21	0.11	-0.01	-0.22	0.32
Ni I	0.06	0.04	0.02	0.01	0.09
Ba II	0.08	0.03	0.01	-0.15	0.17
La II	0.09	0.02	0.04	-0.06	0.12
Eu II	0.08	-0.01	0.04	-0.06	0.15