![]() and NIR observations provide us with information on
stellar populations with different time scales:
and NIR observations provide us with information on
stellar populations with different time scales: ![]() 107 yrs the former
and
107 yrs the former
and ![]() 1010 yrs the latter. The two quantities combined give the ratio
of the current SFR to the average past SFR or
the birthrate parameter b, as defined by Kennicutt et al. (1994).
1010 yrs the latter. The two quantities combined give the ratio
of the current SFR to the average past SFR or
the birthrate parameter b, as defined by Kennicutt et al. (1994).
Following Boselli et al. (2001), we use the Near Infrared luminosity ![]() as
a tracer of the global mass of old stars, assuming that disk galaxies have a constant
as
a tracer of the global mass of old stars, assuming that disk galaxies have a constant
![]() within their optical radius
(Gavazzi et al. 1996c). Thus we write the adimensional parameter b as:
within their optical radius
(Gavazzi et al. 1996c). Thus we write the adimensional parameter b as:
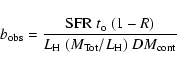 |
(3) |
![\begin{displaymath}%
{\rm SFR} \left[M_\odot {\rm yr}^{-1}\right] = K_{{\rm H\alpha}} L_{{\rm H\alpha}} \left[{\rm erg~s}^{-1}\right].
\end{displaymath}](/articles/aa/full/2002/47/aa2973/img37.gif) |
(4) |
![]() is the dark matter contribution at the optical radius, i.e. within the
is the dark matter contribution at the optical radius, i.e. within the
![]() B band isophote, that we assume
B band isophote, that we assume
![]() 0.5, as in Kennicutt et al. (1994).
0.5, as in Kennicutt et al. (1994).
R=0.3 (Kennicutt et al. 1994) is the fraction of gas that stars re-injected
through stellar winds into the interstellar medium during their lifetime,
that we assume ![]()
![]() 12 Gyrs.
12 Gyrs.
If we assume that galaxies evolved as "closed'' systems following
an exponential
Star Formation History (SFH), with a characteristic decay time ![]() since their epoch of formation (
since their epoch of formation (![]() ), their birthrate parameter
can be computed analytically (see Boselli et al. 2001) as:
), their birthrate parameter
can be computed analytically (see Boselli et al. 2001) as:
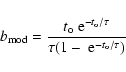 |
(5) |
![\begin{displaymath}%
{\rm log} \tau = -0.4 \left({\rm Log} L_{\rm H} - 12 \right) [{\rm Gyr}]
\end{displaymath}](/articles/aa/full/2002/47/aa2973/img47.gif) |
(6) |
![\begin{displaymath}%
{\rm Log} L_{\rm H} = 11.36 -0.4 H + 2 {\rm log} ({\rm Dist}) [L_{{\rm H}_\odot}].
\end{displaymath}](/articles/aa/full/2002/47/aa2973/img48.gif) |
(7) |
Although b and
![]() EW have distinct dimensions, they are strongly correlated quantities.
In fact they are operationally obtained in a similar way: b is computed by normalizing the
EW have distinct dimensions, they are strongly correlated quantities.
In fact they are operationally obtained in a similar way: b is computed by normalizing the
![]() line intensity
to the NIR continuum intensity, while the equivalent width is divided by the continuum intensity underlying the
line intensity
to the NIR continuum intensity, while the equivalent width is divided by the continuum intensity underlying the
![]() line. This is shown in Fig. 3 which can be
directly compared with Fig. 4 of Kennicutt et al. (1994).
line. This is shown in Fig. 3 which can be
directly compared with Fig. 4 of Kennicutt et al. (1994).
For galaxies in our sample we estimate the "global gas content''
![]() .
.
![]() is available for most (95%) targets by direct 21 cm observations
(see Scodeggio & Gavazzi 1993; Hoffman et al.
1996, and references therein).
The mass of molecular hydrogen can be estimated from the measurement
of the CO (1-0) line emission, assuming a conversion factor (X)
between this quantity and the
is available for most (95%) targets by direct 21 cm observations
(see Scodeggio & Gavazzi 1993; Hoffman et al.
1996, and references therein).
The mass of molecular hydrogen can be estimated from the measurement
of the CO (1-0) line emission, assuming a conversion factor (X)
between this quantity and the ![]() surface density.
X is known to vary in the
range 1020 to 1021 [mol cm-2 (K km s-1)-1]
from galaxy to galaxy, according to their metallicity and UV radiation field. We adopt the empirical calibration
as a function of the H band luminosity:
surface density.
X is known to vary in the
range 1020 to 1021 [mol cm-2 (K km s-1)-1]
from galaxy to galaxy, according to their metallicity and UV radiation field. We adopt the empirical calibration
as a function of the H band luminosity:
| (8) |
The contribution of He, not directly observable, is estimated as
30% of
![]() (see Boselli et al. 2002a).
(see Boselli et al. 2002a).
We define the "gas deficiency'' parameter
![]() as the logarithmic difference between
as the logarithmic difference between
![]() of a reference sample of isolated
galaxies and
of a reference sample of isolated
galaxies and
![]() actually observed in individual objects (in full analogy with
the definition of HI deficiency by Giovanelli & Haynes 1985).
Using a procedure similar to the one adopted by Haynes and Giovanelli (1984)
we find that the gas content of 72 isolated objects
in the Coma Supercluster correlates with
their linear optical diameter (D):
actually observed in individual objects (in full analogy with
the definition of HI deficiency by Giovanelli & Haynes 1985).
Using a procedure similar to the one adopted by Haynes and Giovanelli (1984)
we find that the gas content of 72 isolated objects
in the Coma Supercluster correlates with
their linear optical diameter (D):
![]() ,
where a and b are weak functions of the Hubble type, as listed in Table 2.
,
where a and b are weak functions of the Hubble type, as listed in Table 2.
![]() are listed in Col. 7 of Table 4.
Histograms of the
are listed in Col. 7 of Table 4.
Histograms of the
![]() parameter are given in Fig. 4 for the Coma isolated objects and for the Virgo galaxies. Isolated objects have
parameter are given in Fig. 4 for the Coma isolated objects and for the Virgo galaxies. Isolated objects have
![]() ,
while Virgo galaxies have significantly positive
,
while Virgo galaxies have significantly positive
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2973f4.ps}\end{figure}](/articles/aa/full/2002/47/aa2973/Timg59.gif) |
Figure 4:
Histograms of the
|
Copyright ESO 2002