3 First step: Cross-matching DENIS and 2MASS

   
3.1 Cross-matching strategy

Before running the cross-matching programs, we organized the original data, splitting most of the catalogues into smaller pieces. The DENIS observational strategy had been to divide the sky in strips of $30^{\circ}$ in Declination (Dec) and $12^{\prime}$ in Right Ascension (RA). To define subsamples, we split the DCMC catalogue by strip number because:

• our cross-matching algorithm is well adapted to data files with small extension in RA;
• the cross-matching criterion depends on the strip number as explained below.

There are 119 strip-files covering the LMC. For each strip-file, we extracted from the 2MASS catalogue all the point sources belonging to the same region of the sky. Matches between both catalogues are found by specifying a position search box of a few arcseconds, and comparing the coordinates of entries in both catalogues. The cross-matching program is executed for each strip, starting, each time, with two input files, one from DCMC and one from 2MASS. Both files have been previously sorted by declination, in order to optimize the cross-comparison procedures. Details about the procedure are as follows: for each record of the first file (say, DCMC) we search for all possible cross-matches in the second file (here 2MASS). Among the possible cross-matches, we only keep the one with the smallest difference in position as the most probable counterpart. The actual limits imposed to the positional difference  $\Delta\alpha$ and $\Delta\delta$ depend upon the relative astrometry of the strip (see below).

   
3.1.1 Finding discrepancies in the original catalogues

Cross-matching by position works very well in most cases because the astrometry of DCMC and 2MASS is accurate enough (better than one arcsecond). 2MASS positions were reconstructed from the ACT reference catalogue (Urban et al. 1998), using the Tycho astrometry. The astrometric reference for DCMC positions is the USNO-A2.0 catalogue (Monet et al. 1998). The astrometric solution is global for a strip, minimizing possible inaccuracies of the USNO-A2.0 catalogue in the most crowded regions.

Consequently the match distance is smaller than $0.5^{\prime\prime}$ for the great majority of the stars. There is in principle no risk of confusion at such a small scale. While this is true in general, in practice the cross-matching exercise has proven to be a powerful tool to detect subsets of data which deviate from the perfect situation, and primarily areas suffering from problems in the astrometric or photometric calibration.

In some cases, field distortions in the DCMC affect the quality of the astrometry. To detect and quantify them, we proceeded strip by strip. We kept only well confirmed DCMC sources: $10.5 \leq I \leq 16.5$ and flags in the Iband equal to zero. We ran a cross-matching program based only on distances, with a searching box that goes up to 30 $^{\prime \prime }$. Between all the possible associations found, we kept only the association with $\vert J_{\rm DCMC} - J_{\rm 2MASS}\vert \leq 0.5$. The selection is done on magnitude because in case of field distortions, small distances are not reliable enough a criterion.

The relative shifts in RA and Dec are a function of the pixel coordinates of the camera. We found 11 strips affected by field distortions at a level larger than $2^{\prime\prime}$. We also searched for systematic shifts $\delta J$ and $\delta K_{\rm s}$ between DCMC and 2MASS magnitudes. Mean shifts have been computed for each strip. The diagrams corresponding to the positional and magnitude shifts are all available, strip by strip, on the MC2 web site.

Such astrometric and magnitude shifts depend on the particular strip and had to be taken into account in the DENIS versus 2MASS cross-matching. Strategies for coping with them have been implemented, to allow a proper strip by strip cross-matching of both catalogues. We took advantage of the J and $K_{\rm s}$ common magnitudes of the two surveys. A potential cross-matched source is thus validated not only on a positional criterion, but also on magnitude criteria.

   
3.1.2 Defining a positional searching box

Shifts in RA ( $\delta\alpha$) and Dec ( $\delta\delta$) being mainly a function of the pixel coordinates, they do vary inside one image, but are nearly the same for all the images of the strip. So it is better to use the statistics of the whole strip instead of one single image. Thus we can define a specific position search box for the strip. The size of the box will take into account the shifts in RA and Dec found for this strip number. The default size of the searching box when there are no shifts is $3^{ \prime \prime}$. So we have now an enlarged and asymmetric searching box:

$$\frac{\delta \alpha_{\rm min}^{\prime\prime} - 3^{\prime\prim... ...lpha_{\rm max}^{\prime\prime} +3^{\prime\prime}}{\cos \delta}$$

$$\delta \delta_{\rm min}^{\prime\prime} - 3^{\prime\prime} < \... ... < \delta \delta_{\rm max}^{\prime\prime} +3^{\prime\prime} ,$$

where $\delta \alpha_{\rm min}$, $\delta \alpha_{\rm max}$, $\delta \delta_{\rm min}$, $\delta \delta_{\rm max}$ are the minimum and maximum shifts in RA and Dec (arcseconds). Note that the searching box has a complex shape, since $\delta \alpha_{\rm min} \neq \delta \alpha_{\rm max}$ and $\delta \delta_{\rm min} \neq \delta \delta_{\rm max}$. This box is used to optimise the probability to find the correct cross-matching, even in distorted images.

3.1.3 Selection on magnitudes

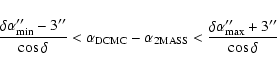
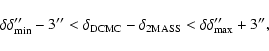
Between all the possible associations found in Sect. 3.1.2, we must keep the best one. We have seen that keeping the association with the smallest distance is no more a reliable criterion because of field distortions. So we have to check the compatibility in magnitude for each association, after applying on the strip data the associated mean magnitude shifts $<\delta J>$ and $<\delta K_{\rm s}>$ computed in Sect. 3.1.1 above.

• If $K_{\rm s}$ is not detected in the catalogues, the selection is done on J. The following relation has to be true to keep the association:
  
  $$\begin{eqnarray*}\vert\delta J - <\delta J>\vert \leq w \times \sqrt {\sigma_ {J... ...iptsize DCMC}}^{2} + \sigma_{J_{\rm\scriptsize 2MASS}}^{2}} ,\\ \end{eqnarray*}$$
  
  where w=2 is a weight, and $\sigma_{J_{\rm\scriptsize DCMC}}$ and $\sigma_{J_{\rm\scriptsize 2MASS}}$ are the relative photometric uncertainties as quoted in both catalogues. Relative uncertainties are in general very small for bright stars, less than 0.01 mag. However, uncertainties on the absolute calibration are much larger: about 0.1 mag for the DCMC. If we apply abruptly the above criterion, we will lose many cross-identifications for the stars with small relative uncertainties. We thus need to refine the selection criterion and consider two cases:

  
  

  $${\rm if} \qquad w \times \sqrt {\sigma_{J_{\rm\scriptsize DCM... ...{\rm\scriptsize 2MASS}}^{2}} \leq \Delta J \qquad {\rm then}$$
  
  
  
  
  $$\vert\delta J - <\delta J>\vert \leq \Delta J \quad$$
  
  
  
  
  $${\rm else~if} \qquad w \times \sqrt {\sigma_{J_{\rm\scriptsize DCMC}}^{2} + \sigma_{J_{\rm\scriptsize 2MASS}}^{2}} > \Delta J$$
  
  
  
  
  $${\rm then} \qquad \vert\delta J - <\delta J>\vert \leq w \ti... ...criptsize DCMC}}^{2} + \sigma_{J_{\rm\scriptsize 2MASS}}^{2}}$$
  
  
  where $\Delta J=0.45$ is the estimated full-width at half-maximum of the $\delta J$ distribution;

• if J is not detected in the catalogues, the selection is done on $K_{\rm s}$ as above but this time we have $\Delta K_{\rm s} = 0.60$;
• if J and $K_{\rm s}$ are detected in both catalogues, the selection is done on J and then on J-$K_{\rm s}$;
• if neither J nor $K_{\rm s}$ are detected in the catalogues, the association is lost.

Applying these criteria, if there are still more than one possible association for one DCMC source, then we keep the association with the smallest $\delta J$ or $\delta K_{\rm s}$.

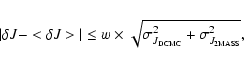
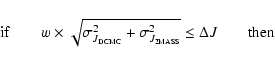
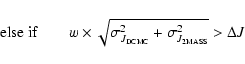
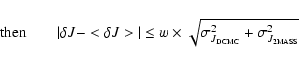
More details about this cross-matching step, as well as the cross-matching criteria used can be found in Delmotte et al. (2001). Nearly 80% of the LMC strips have a match rate better than 90%. The strips with a match rate smaller than 80% correspond to the gaps in the 2MASS data. We checked the distance distribution of the matches, by wether they were done in J, or $K_{\rm s}$or both. There seems to be no relation between the magnitude criterion applied and the distance of the cross-matched source. Figure 3 shows the results of the cross-matching between DCMC and 2MASS, whatever the magnitude criterion was. The mean positional offset between matches is $0.52^{\prime\prime}$ and the modal offset is $0.25^{\prime\prime}$. Figure 4 displays the histograms of the shifts between DCMC and 2MASS in RA and Dec (in arcseconds) for the 119 strips covering the LMC. To check the results, we also compared the distribution of the close matches ($\leq$ $2^{\prime\prime}$) and far matches ($\geq$ $4^{\prime\prime}$) in both the (J-$K_{\rm s}$, $K_{\rm s}$) colour-magnitude diagram and (RA, Dec) plane. Far matches do not show any strange physical behavior and are, as expected, distributed along lines associated with the borders of the strips suffering from field distortions, and also in the center of the Cloud where the density is higher.

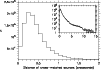Figure 3: Results of the cross-matching between DCMC and 2MASS. Number of objects as a function of the distance of the cross-matched point sources. The bin size is $0.1^{\prime \prime }$.

Figure 4: Histograms of the shifts between DCMC and 2MASS RA and Dec (in arcseconds) for the 119 strips covering the LMC. The bin size is $0.05^{\prime \prime }$ for RA and $0.03^{\prime \prime }$ for Dec.