

Up: On the orbital period
According to Morales-Rueda & Marsh (2002), the presence of
He II 4686 emission during high states could be
the result of disc irradiation
or emission by spiral shocks structures. Therefore,
the detection of He II 4686 in V 592 Her could indicate also
the presence of spiral shocks in this short orbital period system.
Supporting this view is the fact that Baba et al. (2002)
imaged the WZ Sge disk during its 2001 superoutburst
using the He II 4686 line finding
arc-like structures.
Higher quality data than currently available are necessary
to confirm this suspicion in the case of V 592 Herculis.
The period excess is defined as:
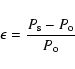 |
(2) |
where 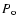 is the orbital period of the binary and
is the orbital period of the binary and 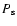 is the superhump period. The period excess is an
important observational parameter in the theory of
disk tidal instability, since it can be related to
the ratio between the stellar masses
q = M2/M1:
is the superhump period. The period excess is an
important observational parameter in the theory of
disk tidal instability, since it can be related to
the ratio between the stellar masses
q = M2/M1:
![\begin{displaymath}1/\epsilon = [0.37q/(1+q)^{1/2}]^{-1}(R_{\rm disk}/0.46a)^{-2.3}-1
\end{displaymath}](/articles/aa/full/2002/44/aah3824/img44.gif) |
(3) |
where a is the binary separation (Patterson 2001).
Here we use Patterson's approximation:
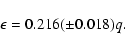 |
(4) |
Using the orbital period
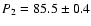 min, along with
the superhump period given by Duerbeck & Mennickent
(1998),
we calculate a period excess of
min, along with
the superhump period given by Duerbeck & Mennickent
(1998),
we calculate a period excess of
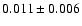 ,
one of the shorter among SU UMa stars (Patterson 2001).
This period excess implies a
mass ratio
,
one of the shorter among SU UMa stars (Patterson 2001).
This period excess implies a
mass ratio
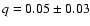 .
If the white dwarf has a typical
mass of
.
If the white dwarf has a typical
mass of
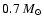 ,
we find
,
we find
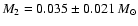 .
Comparing this value with the Kumar limit for Population I stars
(
.
Comparing this value with the Kumar limit for Population I stars
(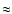
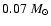 ,
Kumar 1963) we find that
the secondary could be a brown dwarf like object. Only if the white dwarf
is massive (
,
Kumar 1963) we find that
the secondary could be a brown dwarf like object. Only if the white dwarf
is massive (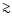
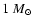 )
is the
mass ratio consistent with a
non-degenerate hydrogen-burning star. On the other hand, if
P1 (91.2 min) is the right period, we obtain
)
is the
mass ratio consistent with a
non-degenerate hydrogen-burning star. On the other hand, if
P1 (91.2 min) is the right period, we obtain
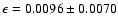 and
and
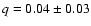 .
The above shows that
our result of a possible brown-dwarf like secondary in V 592 Her
is robust against a
misidentification of the orbital period. In addition,
this finding
in agreement with the result of van Teeseling et al. (1999),
who arrived at this conclusion using considerations about magnitudes
at outburst and quiescence only.
.
The above shows that
our result of a possible brown-dwarf like secondary in V 592 Her
is robust against a
misidentification of the orbital period. In addition,
this finding
in agreement with the result of van Teeseling et al. (1999),
who arrived at this conclusion using considerations about magnitudes
at outburst and quiescence only.


Up: On the orbital period
Copyright ESO 2002
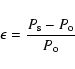
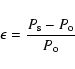
![\begin{displaymath}1/\epsilon = [0.37q/(1+q)^{1/2}]^{-1}(R_{\rm disk}/0.46a)^{-2.3}-1
\end{displaymath}](/articles/aa/full/2002/44/aah3824/img44.gif)