A&A 394, 17-31 (2002)
DOI: 10.1051/0004-6361:20020988
M. T. Hanski 1 - L. O. Takalo 1 - E. Valtaoja 1,2
1 - Tuorla Observatory![]() , 21500 Piikkiö, Finland
, 21500 Piikkiö, Finland
2 -
Department of Physics, 20014 University of Turku, Finland
Received 17 April 2002 / Accepted 1 July 2002
Abstract
Radio light curves of 20 sources from the Metsähovi monitoring program are compared with optical light curves collected from the literature. The Discrete Correlation Function analysis is applied to the data sets. A new qualitative method to study correlations is introduced, where the radio light curves are replaced by model light curves consisting of exponential outbursts. The optical flux level is compared to the phase and flux level of the model flares.
Seven sources show clear correlations using the DCF analysis with six more showing a possible correlation between optical and radio events with time lags from zero to several hundred days. For twelve sources at least one simultaneous optical and radio event is seen. For eleven sources, when comparing optical flux levels with the phase of the model radio outbursts, the optical flux levels were high at the peak of the model radio outbursts. For sixteen sources, when comparing the optical flux level with the radio model flare flux level, the optical flux level was high when radio flux level was high, as well.
Key words: galaxies: active - BL Lacertae objects: general - quasars: general
The search for correlated events between different frequency regimes in active galactic nuclei (AGN) continues. This is due to the increasing amount of data available for more and more sources, thanks to long term monitoring programs. It is clear that there is a connection between optical and radio variability at least in some sources, e.g. 3C 279, 3C 345 (Tornikoski et al. 1994b) and AO 0235+164 (Clements et al. 1995; Raiteri et al. 2001). The smooth UV-to-radio continuum spectra of many AGN indicates a possible connection between these regimes. Also along with radio jets optical jets have been seen in some sources, e.g. 3C 273 (Guthrie & Napier 1975), M 87 (Lelievre et al. 1984), 3C 371 (Nilsson et al. 1997) and 3C 380 (O'Dea et al. 1999).
It is generally accepted that radio outbursts in AGN are triggered by growing shocks in a jet that shoots out from the galaxy center (Marscher & Gear 1985; Valtaoja et al. 1992; Türler et al. 2000). The generalized shock model (Valtaoja et al. 1992; Lainela 1994) explains how a shock grows and decays, and how the outburst looks at different frequencies. The model predicts what kind of time lags are expected between outbursts at different observing frequencies.
So far, light curves are the only way to study the origins of shocks in a jet. Even the innermost parts of jets cannot be resolved with the Very Long Baseline Interferometry (VLBI). The shock component can only be seen in VLBI maps after the most interesting growing phase of the shock is over long ago. If a radio outburst is modelled with an exponential flare (see Sect. 3.2), the observed VLBI component becomes, in general, visible when the shock is already decaying and 2/3 of the model outburst has already taken place (Savolainen et al. 2002).
Correlations between different frequency regimes in AGN have been searched for since the beginning of the 1970's. Individual objects have been studied in many papers, e.g. 3C 120 (Usher 1972), BL Lac (Andrew et al. 1974; Tornikoski et al. 1994a), PKS 0420-01 (Dent et al. 1979), 3C 446 (Bregman et al. 1988), OJ 287 (Kikuchi et al. 1973; Kinman et al. 1974; Usher 1979; Valtaoja et al. 1987) and AO 0235+164 (Balonek & Dent 1980; Roy et al. 2000; Raiteri et al. 2001).
The first studies containing several sources were carried out by Usher (1975) and Pomphrey et al. (1976). Usher (1975) studied the correlation between radio spectral index and optical variability. Pomphrey et al. (1976) studied optical and radio light curves and found a strong correlation between optical and radio only in one object, OJ 287. A very ambitious search for correlations in 45 AGN's was done by Balonek (1982; hereafter B82). Of the sources studied, 11 exhibited a likely correlation between optical and radio with time lags up to several hundred days. Correlations were not found in 15 sources. Other extensive studies were done by Tornikoski et al. (1994b; hereafter T94) and Clements et al. (1995; hereafter C95), who both studied a large sample of AGN.
In T94 a clear correlation between optical and radio was found in 10 sources of the 22 studied. In C95 nine of the 18 sources showed radio-optical correlations. In both these studies and in this paper, the discrete correlation function (DCF) is used for correlation analysis. It is, however, insufficient to calculate the DCF values alone, because sometimes the DCF gives results that are not real features. Other methods are needed to confirm the results from the DCF analysis. In T94, C95, and this paper, the DCF analysis is complemented with visual inspection. We introduce also a new qualitative method for studying correlations.
We compare the optical light curves with the 37 and 22 GHz light curves for several quasars and BL Lac objects, first by using the DCF, and also by modelling the radio light curve with a set of exponential flares, and comparing optical flux level with the phase and the flux level of the concurrent radio flares.
| Source | Other names | Redshift | Type of Object | References | Previous correlation studies |
| 0109+224 | S2 0109+22 | ? | BLO | 5, 11, 13, 15 | - |
| 0219+428 | 3C 66A | 0.444 | BLO | 5, 7, 13, 14, 15 | B82 |
| 0235+164 | AO 0235+16 | 0.94 | BLO | 1, 9, 12, 15 | BD80, B82, C95, W00, R01 |
| 0420-014 | PKS 0420-01 | 0.915 | HPQ | 1, 8, 12 | P76, D79, B82 |
| 0422+004 | PKS 0422+00 | 0.31 | BLO | 4, 5, 6, 8, 13, 14, 15 | - |
| 0735+178 | PKS 0735+17 | >0.424 | BLO | 1, 5, 12, 13, 14, 15 | U75,P76, B82, HB92, T94, C95 |
| 0736+017 | PKS 0736+01 | 0.191 | HPQ | 5 | U75, P76, B82, T94 |
| 0754+100 | OI 090.4 | 0.66 | BLO | 3, 4, 5, 13, 14, 15 | - |
| 0851+202 | OJ 287 | 0.306 | BLO | 1, 5, 7, 12, 13, 14, 15 | U75, P76, U79, B82, V87, HB92, T94, C95 |
| 1156+295 | 4C +29.45 | 0.729 | HPQ | 4, 5, 8, 11, 12, 13 | T94, C95 |
| 1219+285 | W Comae | 0.102 | BLO | 5, 10, 12, 14, 15 | U75, B82, T94 |
| ON 231 | |||||
| 1226+023 | 3C 273 | 0.1583 | LPQ | 3, 5, 8, 11 | U75, P76,B82, T94, C95 |
| 1253-055 | 3C 279 | 0.5362 | HPQ | 5, 11 | B82, T94 |
| 1633+382 | 4C +38.41 | 1.814 | LPQ | 5, 8, 11 | - |
| 1641+399 | 3C 345 | 0.5928 | HPQ | 1, 5, 8, 12 | U75, B82, HB92, T94 |
| 1749+096 | 4C +09.57 | 0.322 | BLO | 4, 15 | B82, T94, C95 |
| 1807+698 | 3C 371 | 0.051 | BLO | 5 | U75, P76, B82, T94 |
| 2200+420 | BL Lac | 0.0686 | BLO | 2, 5, 12, 13, 15 | U75, P76, B82, B88, HB92, T94, C95 |
| 2223-052 | 3C 446 | 1.404 | HPQ | 1, 12 | U75, P76, B82, HB92, T94, C95 |
| 2251+158 | 3C 454.3 | 0.859 | HPQ | 1, 5, 8, 12 | U75 |
From the Metsähovi radio monitoring list we selected objects for which the radio light curves were extensive enough for the analysis, i.e. there was enough data for an attempt to apply the total radio flux density decomposition to separate flares (see Sect. 3.2), and for which sufficient amount of recent optical data was found. Details of the Metsähovi radio monitoring program and the radio data are described in Salonen et al. (1987), Teräsranta et al. (1992) and Teräsranta et al. (1998). Our sample consists of 20 AGN, of which 9 are quasars and 11 BL Lacs.
The objects are classified as "BLO''![]() Lac object, "HPQ''
Lac object, "HPQ''
![]() optical Polarization Quasar, "LPQ''
optical Polarization Quasar, "LPQ''
![]() optical Polarization Quasar. The quasar / BL Lac classifications are adopted from Véron-Cetty & Véron (2001).
optical Polarization Quasar. The quasar / BL Lac classifications are adopted from Véron-Cetty & Véron (2001).
The optical data is collected from several articles. References are given in Table 1. The optical data is from all optical frequency bands (U, B, V, R and I). The data was first converted to the optical V-band by using colour information calculated from the data, because the colours may not be constant with time. The calculated colours were checked with results given in Véron-Cetty & Véron (2001), and if there were not enough data points for calculation, the colours from the catalogue were chosen instead. Transformations from magnitudes to flux densities were done according to Mead et al. (1990).
 |
Figure 2:
Autocorrelation ( ACF) and cross correlation ( DCF) results for BL Lac. The time lag |
The Discrete Correlation Function (DCF) was introduced by Edelson & Krolik (1988). It was specially developed for correlating unevenly sampled data sets, such as light curves in astronomy. Hufnagel & Bregman (1992) generalized it and used it to correlate optical light curves with radio light curves at frequencies 4.8, 8.0, and 14.5 GHz.
In this paper the form adopted from Hufnagel & Bregman (1992) is used. It goes as follows.
First, the set of unbinned discrete correlations (
UDCFij) are calculated between each pair (ai,bj) in data sets a and b.
UDCFij is defined as
The DCF method is good in the sense that all the data is used and there is no need to interpolate or use artificial data points. This method also gives a reasonable error estimate. It doesn't, however, work well if the data sets are too differently sampled or the bin size in the two light curves to be correlated is very different. Also, if the gaps in the data are long or frequent, the DCF might give wrong correlations. One has to be careful when examining the results, because e.g. the length of a data set or the lenghts of the gaps in data sets may show in the DCF results as positive peaks. The correlations given by the DCF have to be confirmed by other methods, like visual inspection here, before tentatively accepting them as real. As an example of the data, light curves for BL Lac are shown in Fig. 1. The corresponding correlation analysis is shown in Fig. 2.
It has been shown that total flux density (TFD) variations in radio regime can be modelled as a sum of a constant quiescent flux component and a small number of model flare components with exponential rise and decay (Valtaoja et al. 1999). The quiescent flux is caused by the approximately constant background flow in the jet. The outbursts that are modelled with exponential flares are caused by shocks in the jet.
The model flare is of the form:
The TFD decomposition to separate model flares works like CLEAN-algorithm. First, a model flare is fit to the brightest radio flare and substracted from the TFD light curve. This is repeated until there are no significant radio flares left in the light curve. Then the model flare parameters are adjusted by fitting the combined model flares to the real light curve. Of course, a better and better fit can be obtained by adding more and more model flares even to the smallest variations. It is difficult to estimate which variation is a real flare and which is not meaningful. Here this rule of thumb is used: bright flares don't occur more often than approximately once a year, unless it is a double flare. The only exception here is OJ 287. For that source, the outbursts occur more often, especially after 1985. As an example the TFD decomposition for BL Lac is shown in Fig. 3.
The phase of a model flare ![]() is defined as follows:
is defined as follows:
The idea of this method is to replace the real radio light curve with a set of model flares that represent the total flux density variations. Thus small flickering and noise are neglected and only real outbursts are analyzed. Phase and brightness can be defined for a model flare at any epoch. We can therefore connect to each optical data point a set of numbers characterising the concurrent radio status of the source.
At each epoch of optical observation the phase and the brightness of each model radio flare are calculated, along with the total radio brightness calculated by adding the model flares together (see Fig. 3). At each optical observation epoch we take only the brightest two model flares into account. The optical flux is divided between them by linear weighting (i.e., if the first radio flare is at that epoch twice as bright as the next brightest, the optical flux is divided between them at ratio 2:1). The optical flux level is then plotted against the phase and the flux level of the concurrent model radio outburst(s) and against the total flux level of the model light curve. The abscissa is then divided into ten bins. An average of the optical flux is calculated in each bin. The error bars indicate the standard error of the mean in the bin. Thus, having the information of the optical flux against information of all the radio flares in the same figure, we can compare the optical flux levels and the radio status.
For example, if we find that optical flux levels corresponding to the rising part of the radio flare tend to be higher than those on the decaying side, we can say that radio and optical regimes are correlated, even though such a correlation might not show up in the DCF analysis, due to unsufficient data or variable time delays.
Similarly, a comparison of the average optical and radio flare flux levels might reveal a non-random trend indicating a possible correlation in the overall radio and optical behaviour.
An example of such a comparison is shown in Fig. 4.
The first graph shows the dependence of the average optical flux level vs. the phase of the model flare ![]() in the case of BL Lac. It can be seen that the optical flux level tends to be high during the rise of the radio flare and lower during the radio flare decay phase, indicating that the two regimes are connected.
in the case of BL Lac. It can be seen that the optical flux level tends to be high during the rise of the radio flare and lower during the radio flare decay phase, indicating that the two regimes are connected.
The second graph shows the average optical flux level vs. the model radio flare flux level. The third graph shows the average optical flux level vs. total radio flux level calculated by adding model flares to form an model light curve. It is obvious that for BL Lac, high radio flux levels do not coincide with high optical flux levels. On the contrary: the highest optical flux level tends to occur at intermediate or low radio flux levels. One possible explanation for this is that, on the average, optical events tend to precede radio events by a significant amount, as indeed the correlation analysis also indicates.
In the DCF analysis a bin size of 50 days was used. Several other bin sizes from 30 to 100 days were tried, but 50 days seemed to give, on the average, the best results. The DCF analysis was complemented with visual inspection. The visual inspection was made by shifting light curves in respect to each other, trying different time lags. This analysis was done by using the whole light curves, and also by using only parts of the light curves. The visual inspection was performed both before the correlation analysis in order to find independent results, and after the analysis in order to confirm the results given by the DCF. The DCF was also calculated for the 37 and 22 GHz light curves. The correlation between the two radio frequencies was strong for all of the sources, the time lags were zero or small.
For most of the sources the model radio flare fit was successful. For sources that show only modest radio flux variations, reliable model flare fits are impossible.
At the epoch of each optical data point the phase and the brightness of concurrent model radio outbursts were calculated. The phase ![]() gets values between [0,2], and the brightness of model radio outbursts, as well as the brightness of the composite model light curve, gets values from minimum flux to maximum flux that are calculated for each source individually.
These ranges were divided into ten bins and the average of the optical flux level was calculated for each bin (see e.g. Fig. 4).
gets values between [0,2], and the brightness of model radio outbursts, as well as the brightness of the composite model light curve, gets values from minimum flux to maximum flux that are calculated for each source individually.
These ranges were divided into ten bins and the average of the optical flux level was calculated for each bin (see e.g. Fig. 4).
For each source we identified the radio phase at the time of the highest average optical flux level.
In Table 2 the phase of the model radio flare is marked with "-'' if the phase ![]() ,
"-'' when
,
"-'' when
![]() ,
"0'' when
,
"0'' when
![]() ,
"+'' when
,
"+'' when
![]() and "++'' when
and "++'' when ![]() .
The "-'' signs therefore refer to developing stage of model radio outbursts and "+'' signs the decaying stage of the outbursts.
.
The "-'' signs therefore refer to developing stage of model radio outbursts and "+'' signs the decaying stage of the outbursts.
In comparing the average optical and radio flux levels we divided the sources into three categories based on the type of dependence found. In the first category, marked with "d/D'', are the sources in which the highest optical flux levels occur during the dimmest third of the radio flux level. In the second category ("m/M''), are the sources in which the highest optical flux levels occur during the middle third of the radio flux level. In the third category ("b/B'') are the sources in which the highest optical flux levels occur during the brightest third of the radio flux level. As an example see Fig. 8 and explanation in the text for the source.
In the following we discuss each source individually. In this paper we only show some of the figures, selected in order to show typical features for each step of the analysis. The figures for all the sources are available in electronic form.
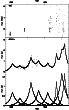 |
Figure 7: The TDF decomposition to individual outbursts for S2 0109+224 37 GHz light curve (see Fig. 3 for further explanation). |
 |
Figure 8:
Optical flux level vs. the phase |
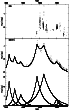 |
Figure 11: Same as Fig. 7 for PKS 0735+178. |
 |
Figure 12: Same as Fig. 8 for PKS 0735+178. |
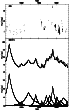 |
Figure 17: Same as Fig. 7 for 2251+158 (3C 454.3). |
 |
Figure 18: Same as Fig. 8 for 2251+158. |
This source has been intensively monitored since 1995 (Figs. 5-8). The DCF shows a strong correlation between the optical and the 37 GHz and the 22 GHz events with time lags of approximately 350 days and 400 days, respectively. The time lag between 37 GHz and 22 GHz is 0-50 days. Visual inspection confirms these results.
The model flare fit to radio light curves was successful. The brightest optical flux levels do not occur at the time of the brightest radio flux, but rather at 2/3 of the maximum radio flux levels (Fig. 8). This is expected, since the time lag between optical and radio is large.
This source has been monitored optically frequently since 1993. Radio monitoring for this source started at the same time. In the optical bands this source is very active, showing several bright outbursts. After 1997 the optical activity settled down. The DCF shows a possible correlation between optical and both the radio bands with a time lag of c. 400 days. Visual inspection shows that this is also possible, although some possible simultaneous events are present as well (e.g. 1996). The time lag between the radio frequencies is 0-50 days.
The model flare fit is not very good, because the radio flux variations are small. Nevertheless, the fit shows the trends in variations fairly well. The brightest optical flux levels seem to coincide with fairly bright radio flux levels at the rising part of the radio flares (i.e., the shock is growing).
B82 found no correlations between optical and radio for this source.
This source has been monitored intensively since 1986 at Metsähovi. The optical light curve reaches back to 1976. The source shows large variations in all the studied frequency bands. The DCF doesn't reveal strong correlations, but it shows a possible correlation with a small time lag between the optical and the 37 GHz light curves. Visual inspection shows the possible correlation as well. At least two radio outbursts coincide with simultaneous optical flares (1987 and 1998).
The model flare fits were successful, especially after 1986. The brightest optical flux levels occur, on the average, in the rising part of the radio flare. The optical flux levels tend to be high when the radio flux levels are high.
Balonek & Dent (1980) and B82 found correlations with no time lag. C95 agreed with these results. Webb & Malkan (2000) studied the outburst in 1997, and suggested that variations in the optical bands and in the radio frequencies at 14.5, 8.0 and 4.5 GHz were a result of a microlensing effect, while earlier outbursts were not. Raiteri et al. (2001) found optical variability correlated with radio with a time lag of 0-60 days.
This source shows variability at all frequencies. Several bright optical outbursts have been observed since 1990. The radio light curve time coverage is good after 1987. The DCF doesn't reveal any strong correlation between optical and radio events with optical events leading radio events. A possible correlation can be seen with a time lag of 0-200 days, though. Visual inspection doesn't give any clear correlations, either. Some possible simultaneous events are present (e.g., the outbursts in 1985 and in Feb. 1991).
The model flare fits were successful after 1990. The brightest optical flux levels seem to occur, on the average, after the radio outburst peak at both the radio frequencies. The optical flux levels are high when radio flux levels are high, too.
Pomphrey et al. (1976) found a possible correlation with optical leading radio events by 0.2 years. Dent et al. (1979) found evidence for optical events leading radio events by 2.2 years. B82 found possible correlations between optical and radio with several time lags between 1-2 years. Also, one simultaneous event was recorded. The best correlation function result was with a 1.75 year time lag.
The light curves of this source are fairly densely sampled. In the optical bands the source is very variable. At the radio frequencies the sampling is less frequent. The DCF didn't show any strong correlations. A weak correlation is seen with a time lag of c. 250 days. The highest DCF value is at 900-day time lag but that may not be a real feature. Visual inspection doesn't reveal clear correlations, although one possible simultaneous event is present (c. 1994.9).
The model flare fits were quite good, although the small variability in the radio light curves made fitting the model flares difficult. The brightest optical flux levels occur, on the average, in the rising part of the radio flares, and the radio flux levels are high, as well. This suggests that the possible time lag between optical and radio events is not large.
The optical and radio light curves are extensive. The optical data used in this analysis reaches back to 1989 and the radio light curves start from 1980. The 22 GHz and 37 GHz events are strongly correlated without time lag. No mathematical correlation was found between optical and radio events for this source. Visual inspection shows a possible simultaneous event in 1991, and that both optical and radio activity decrease after 1992 (see Figs. 9-12).
The model flare fit was successful. The optical flux level is, on the average, highest when the radio flare has its peak at 37 GHz and reaching maximum at 22 GHz.
Pomphrey et al. (1976) found a possible correlation in one event, with radio events leading optical events by 0.88 years. B82 found a visual correlation between optical and radio variability in this source. Also, with post-1976.5 optical and radio data there is a clear correlation with a small or zero time lag. Hufnagel & Bregman (1992) found no significant correlations for this source between optical and radio. No clear correlation was found by T94 between optical and radio, but at least one optical flare coincided with a radio event (c. 1990). No correlation was found between optical and radio for this source by C95.
There are too few optical data points to draw any conclusions about correlations between optical and radio in this source. A possible simultaneous event in optical and radio is present at the end of 1996.
The model flare fit is reasonably good but the optical data points are in three clumps which occur when the radio flux is bright at both radio frequencies. The analysis therefore gives a good correlation between the radio and optical flux levels, but the result may be misleading.
Neither Pomphrey et al. (1976), B82 nor T94 found any correlation between the optical and radio events for this source.
The model flare fit is good throughout the 1990's. The optical flux levels tend to be high, on the average, in the rising part of the radio flares, and the radio flux levels are still roughly half of the maximum value. This suggests a longer time lag and agrees with the DCF results.
The model flare fits were succesful, although the problem with outbursts overlapping each other is seen here as well. Comparing the optical flux level with the radio model flare flux level and phase is hard, because it is impossible to estimate to which model radio flare a certain optical data point should be connected.
Pomphrey et al. (1976) found a good correlation between optical and radio (2.8 cm) for this object only. B82 found a signifiant correlation between optical and radio events, with no time lag before 1973, and with a one-month time lag since 1974. Valtaoja et al. (1987) studied the optical and 4-37 GHz radio light curves and found that the typical time lag between optical and radio is from 0.12 to 0.54 years. Hufnagel & Bregman (1992) found optical leading radio 8 GHz by 200-800 days. T94 found a fair correlation with a zero time lag, and with other time lags as well. C95 found optical and radio correlated by time lags of either 0-2 months or 9-15 months.
This source is quite intensively monitored in radio but the optical light curve contains long gaps. This source is very variable in both the optical and radio frequencies. The DCF shows peaks at time lags of 450 and 600 days, but these cannot be confirmed by visual inspection. Visual inspection reveals a possible correlation with a time lag of approximately 150 days (see Figs. 13-14).
The model flare fit is good after 1986. The optical points after 1990 only are taken into account for this analysis. The optical and radio flux levels are, on the average, high at same time. This cannot be confirmed by inspecting the optical flux levels against the phase of the radio flares.
T94 found a correlation between optical and radio data with a time lag between 500 and 600 days. C95 saw a major peak in DCF at a 600 days' time lag, but could not confirm the result with visual inspection.
This source was quiet in optical from the beginning of the 1970's to 1986. Since 1988 it started showing activity in optical. In radio the small activity seems to quiet down after 1993. The DCF doesn't show any correlations between optical and radio. Visual inspection reveals no correlations, either.
The model flare fit was successful after 1986. The optical flux level is brightest after the radio outburst peaks at 37 GHz. The result may be misleading, because the only bright optical outburst occurs just after the last radio outburst. The radio flux levels tend to be low when the optical flux levels are high. At 22 GHz the optical flux levels are high when radio flares are, on the average, at their last decaying stage.
Neither B82 nor T94 found correlation for this source.
The radio data sets are extensive and reach back to 1980. The optical light curve studied here is sparser and covers only about 2000 days from 1993. The correlation function has a peak at a time lag of 1000 days. Visual inspection shows that this is possible. More optical data points are needed in the future to confirm this.
The model flare fit was very successful, because both the radio data sets were extremely well sampled. On the average, the brightest optical flux level occurs after the model outburst peaks at 22 GHz, and at the end of the radio flare at 37 GHz. The model radio flare flux level is intermediate at both the radio frequencies when the optical flux level is, on the average, highest.
B82 found no correlation between optical and radio for this source, neither did T94 nor C95. There are other studies as well, like Valtaoja et al. (1991) and Robson et al. (1993), where clear correlations between some optical and radio events have been found.
This source has been monitored frequently in optical bands since the 1970's. Radio light curves reach back to 1984. The DCF doesn't show correlations between optical and radio. The high DCF value at a 950-day time lag is probably due to the length of the optical light curve. Visual inspection shows similar simultaneous behaviour between different frequency bands until the last optical outburst.
The model flare fits were succesful. The optical flux levels are high, on the average, at the end of the radio flare at 37 GHz and at the peak of the radio flare at 22 GHz. However, if the last optical outburst is excluded (because visual inspection indicates possible simultaneous behaviour until the last optical outburst), the brightest optical flux level coincides with the highest radio flux levels at both the radio frequencies at the peak of the radio flare.
B82 found no correlation between optical and radio. T94 found a strong correlation between optical and radio with no time lag.
The optical data set for this source is short. Radio events have been monitored since 1982. Visual inspection shows a simultaneous optical and radio event in 1995. The DCF doesn't reveal any correlations between optical and radio.
The model flare fit is fairly good. There is no clear correlation between the optical and radio flux levels. The optical flux level is, on the average, highest when the radio flux levels are low/intermediate at 37 GHz and high at 22 GHz. The phase of the radio flare at both the radio frequencies, when the optical flux level is high, indicates a long time lag, if there is a correlation.
The historical optical light curve of this source reaches back to 1970. The radio monitoring in Metsähovi started in 1980. There is a very active period in both optical and radio between 1990 and 1993. Some events are clearly simultaneous. The DCF doesn't give any single time lag, rather the DCF peak is quite broad. However, visually it is obvious that the optical events correlate well with the radio events.
The model flare fit was successful. There the simultaneity can easily be seen. The optical flux level is, on the average, highest when the radio flux level is high as well, and the radio flares have peaks at both frequencies.
B82 found no significant correlations between optical and radio. Hufnagel & Bregman (1992) found a possible correlation between the optical and the 14.5 GHz radio with a time lag of 100-400 days. T94 found simultaneous optical and radio events.
The optical light curve of this source is short, but optical outbursts seem to coincide with radio flickering at the same time, although the amplitude is different.
The flare fit is reasonably good after 1990. Because there are so few optical data points it is hard to say anything conclusive.
T94 found at least one simultaneous event between optical and 90 GHz. C95 found a correlation with optical events leading radio events by 2 months.
The optical light curve is, again, too short for effective analysis. The optical brightening at 1997 is simultaneous with a flux rise at 37 GHz.
The flare fit is not very good. The radio data is noisy and variability small.
Neither B82 nor T94 found correlations between optical and radio for this source.
BL Lac is strongly variable at all the frequencies studied here (see Figs. 1-4). The optical light curve starts in 1971 and radio light curves in 1979. The variability is so fast and flares occur so often that DCF analysis is not very reliable. The DCF gives best correlation with a time lag of 700-750 days. There are also possible simultaneous events. The optical data set contains large gaps. This makes comparison between optical and radio difficult.
The model flare fit was successful. Comparing optical flux level with radio flux level is difficult, because the events in both are frequent and fast. It is hard to say to which radio outburst an optical data point associates with. The results, however, seem to agree with the DCF results. The radio outburst phase and flux level, when the optical flux level is highest, indicate a large time lag between optical and radio events. This agrees with the DCF results well.
Pomphrey et al. (1976) found no obvious overall correlation between optical and radio, but a possible time lag of 0.5 years with optical leading radio was seen. B82 found a correlation between optical and radio events in post-1980 data, but also claims that there is no significant overall correlation between these regimes. Hufnagel & Bregman (1992) found a weak correlation between optical B-band and radio (14.5 and 8 GHz) with a time lag of 1-2.5 years. T94 said that all optical events after 1980 were semi-simultaneous or simultaneous with radio outbursts. C95 found that the optical and radio data prior to 1977 are correlated with a time lag of two months, but after 1977 the correlations disappear.
The optical light curve of this source is long and radio light curves reach back to 1985. The optical activity coincides with activity at the radio frequencies. Simultaneous events are seen. The DCF gives a possible correlation between optical and radio with a time lag of about 200 or 300 days. Visual inspection doesn't rule these out, but cannot confirm them, either.
The model flare fit was successful. Comparison between the optical flux levels and the radio flux levels give different results for 37 and 22 GHz data. At 37 GHz the radio flux is, on the average, high or intermediate when the optical flux level is high in the rising part of the radio flare. At 22 GHz the highest optical flux levels occur at the lowest radio flux levels at the beginning of radio flares.
Pomphrey et al. (1976) found no significant correlation between optical and radio. B82 found a possible correlation with optical events leading radio events by ca. 500-600 days. Bregman et al. (1988) found optical-radio correlation with optical leading radio by 400-600 days. Hufnagel & Bregman (1992) found possible correlation between optical and radio with a time lag of 1-2 years with a mean variance correlation method. The DCF analysis showed no significant correlation. T94 found simultaneous or nearly simultaneous optical and radio events.
The data sets are very good in radio and fairly good in optical. In optical there are several gaps. Some events are clearly simultaneous, like the bright outburst in 1993. The DCF gives a strong correlation with no time lag between optical and radio (see Figs. 15-18).
The model flare fit is good. The comparison between optical flux levels and radio flux levels gives similar results with the DCF. The optical flux level is, on the average, high when the radio flux level is high. At 37 GHz the highest optical flux occurs at the peak of the radio flares. At 22 GHz there is no clear preferred phase of radio flares where the optical flux levels are high.
Pomphrey et al. (1976) found a possible correlation with optical leading radio events by 1.2 years. B82 found a possible correlation between optical and radio with time lags of 180, 285, and 310 days. T94 found simultaneous events. C95 didn't find correlations between radio and optical events.
| Source | S37 | S22 | S37t | S22t | Results of other studies | |||
| 0109+224 | 350-400 | ++ | 0 | b | m | B | B | - |
| 0219+428 | ca. 400 VIS | - | - | b | b | M | B | B82(NC) |
| 0235+164 | - | - | b | b | B | D | B82 and BD80 ( |
|
| 0420-014 | 0-200? VIS | + | + | b | b | B | B | P76 (0.2 yr?), D79 (2.2 yr), B82 (1-2 yr, not constant) |
| 0422+004 | 250? VIS? | - | 0 | b | b | B | B | - |
| 0735+178 | VIS | 0 | - | b | b | B | B | P76 (-0.88 yr?), B82 ( |
| 0736+017 | VIS? | 0 | - | b | m | B | B | P76 (NC), B82 (NC), T94 (NC) |
| 0754+100 | 200 or 500 | - | 0 | d | b | D | D | - |
| 0851+202 | ca. 750? VIS | ++ | ++ | b | m | M | M | P76 (0.875-0.60 and 0 yr), U79 (6 months), V87 (2-6 months), HB92 (400 days), T94 (0 d and others), C95 (0, 1-2 and 11 months) |
| 1156+295 | 450 or 600? | - | ++ | b | b | D | B | T94 (500-600 days), C95 (NC) |
| 1219+285 | NC | 0 | ++ | m | d | M | D | B82 (NC), T94 (NC) |
| 1226+023 | 1000? | ++ | 0 | m | m | M | B | P76 (NC), B82 (NC), T94 (0-200 days?), C95 (NC) |
| 1253-055 | VIS | 0 | 0 | b | b | B | B | B82 (NC), T94 (0 days) |
| 1633+382 | VIS | - | - | d | b | B | M | - |
| 1641+399 | 0-300 VIS | 0 | - | b | b | B | B | B82 (NC or 720 days), HB92 (100-400 days), T94 (0 days) |
| 1749+096 | VIS? | 0 | 0 | b | b | B | B | T94 (marginal?), C95 (2 months) |
| 1807+698 | VIS | + | + | b | b | B | B | P76 (0.5 yr?), B82 (NC), T94 (NC) |
| 2200+420 | 750-800 VIS | - | ++ | d | d | D | D | P76 (NC), B82 (NC), Bregman et al. (1988) (400-600 days), HB92 (400-800 days), T94 (200-300 days) |
| 2223-052 | 200? VIS | - | - | m | d | B | D | P76 (NC), B82 (520-560 days), HB92 (NC), T94 ( |
| 2251+158 | 0 VIS | 0 | - | b | m | B | B | P76 (1.2 yr), B82 (180-310 days), T94 (0-100 days), C95 (NC) |
The DCF gave a clear correlation for seven sources and a possible correlation for six more sources. For 12 sources, at least one clearly simultaneous outburst was seen in visual inspection. Of these, seven did not show significant correlations in the DCF analysis.
The new method we have introduced, a comparison between optical flux levels and radio model flares, can reveal statistical correlations between the two regimes in cases where the data is not sufficient for correlation analysis or visual inspection. A source with simultaneous radio and optical variations should in our analysis have its average optical flux strongest at the peak of the model radio outbursts (denoted by "0'' in Table 2). Furthermore, there should be a positive correlation between average optical and radio flux levels (denoted by "b/B'' in Table 2). A source for which optical variations precede the radio variations should have its average optical flux strongest during the rising part of the model radio outburst (denoted by "-'' or "-'' in case of a longer time delay). The highest average optical flux levels should correspond to medium (or dim) average radio flux levels (denoted by "m/M'' or "d/D'' in case of a longer time delay).
An example of "a nearly perfect case'' is 1253-055 (3C 279), which lacks only a significant DCF correlation.
For 11 sources the optical flux levels, on the average, are highest at the peak of the model radio outbursts (at least for one of the radio frequencies).
For 16 sources the highest optical flux level occurs during the highest radio flare flux levels at least for one of the radio frequencies. Sixteen sources also show a similar correlation to the modelled total radio flux.
Another problem is that there are probably other mechanisms triggering optical outbursts than just shocks in a jet. In the optical regime there are at least two emission components: synchrotron and thermal. The synchrotron component probably is of the same origin as the radio emission, which is also synchrotron emission. The thermal optical emission, on the other hand, probably has no radio counterpart. This means that in one source optical flares can occur both with and without radio counterparts. Such is the case in the best studied source OJ 287 (Valtaoja et al. 2000).
Also, it seems that "too much'' data makes correlation analysis difficult. Throughout this analysis the optical data was binned in one day bins. Normally this binning is good, because there are not that many data points. However, for some sources in this study, namely OJ 287, BL Lac, 3C 66A and AO 0235, it might be reasonable to use larger bins, say a week for optical light curves. The best bin size would probably be approximately that used for the radio data, too.
In this paper we studied correlations between the optical light curve and the 37 and 22 GHz radio light curves. The sample was 20 active galaxies, of which 11 are BL Lac objects and 9 are quasars. The analysis was done using the discrete correlation function (DCF). The seven sources that showed a clear correlation were S2 0109+22, 3C 66A, AO 0235+16, OI 090.4, 3C 345, BL Lac and 3C 454.3. A possible correlation between optical and radio events was found in six more sources: PKS 0420-01, PKS 0422+00, OJ 287, 4C 29.45, 3C 273 and 3C 446. No correlation was found in sources PKS 0735+17, PKS 0736+01, ON 231, 3C 279, 4C 38.41, 4C 09.57 and 3C 371. Of these sources PKS 0736+01, 4C 09.57 and 3C 371 had a very limited amount of optical data.
There are no clear rules for defining which correlations given by the DCF are significant and which are not. Some good instructions were given by Hufnagel & Bregman (1992). A rule of thumb used here is that the correlation is real if it can be confirmed by another method. It is also good to notice that due to sampling or gaps in the light curves the DCF analysis may miss some real correlations that are seen in the visual inspection of the light curves. Using visual inspection, for twelve sources at least one simultaneous event in optical and radio was seen (3C 66A, AO 0235+16, PKS 0420-01, PKS 0735+17, OJ 287, 3C 279, 4C 38.41, 3C 345, 3C 371, BL Lac, 3C 446 and 3C 454.3).
A new qualitative method to study correlations was introduced. The radio light curves were replaced by model fit light curves that consist of flares that have exponential rise and decay. At each optical observation epoch the phase and the brightness of the individual outbursts and the brightness of the model light curve were calculated. The optical flux level was then compared with the phase and the flux level of the coincident individual outbursts, as well as with the flux level of the composite model light curve.
In practice, our method is similar to interpolation of radio data in order to determine the radio flux at the time of each optical observation. However, the advantage of our method in comparison with, e.g., spline interpolation, is that we use an exponential interpolation function which appears to provide a realistic description of radio flare evolution (Valtaoja et al. 1999). Our model fitting not only provides an estimate of the total radio flux at any given epoch, but also parameters (phase and flux) of the individual radio flares at the time of each optical observation. We can therefore also search for overall statistical connections, such as whether optical flaring tends to occur during the rise or the decay of radio flares.
We agree with T94 that radio-optical connections would be found in many sources, were there more frequent observations in both optical and radio bands. However, even with fully sampled optical and radio flux curves statistically significant correlations might not be found by using the whole data. Individual flaring events in a single source can have variable time delays, and some events may even be clearly simultaneous in both radio and optical regimes. Examples of such behaviour can be seen in e.g., BL Lac (this paper, T94 and Tornikoski et al. 1994a). In addition, at least some sources appear to have both thermal and non-thermal optical events, e.g. OJ 287 (Valtaoja et al. 2000).
With these caveats, we summarize the results of our new method as follows.
For 11 sources the optical flux levels were high at the peak of the radio outburst at least for one of the radio frequencies: S2 0109+224, PKS 0422+00, PKS 0735+17, PKS 0736+017, OI 090.4, ON 231, 3C 273, 3C 279, 3C 345, 4C 09.57, 3C 454.3). For ON 231 this was the only evidence of correlation found. Also the flux levels of the model outbursts were high when the optical flux level was highest for 16 sources at least for one of the radio frequencies: S2 0109+224, 3C 66A, AO 0235+16, PKS 0420-01, PKS 0422+00, PKS 0735+17, PKS 0736+01, OI 090.4, OJ 287, 4C 29.45, 3C 279, 4C 38.41, 3C 345, 4C 09.57, 3C 371, 3C 454.3.
Acknowledgements
This work has been supported by Finnish Academy of Sciences projects number 875067 and 863510.
Figure 1:
Light curves for BL Lac.
Figure 2:
Autocorrelation ( ACF) and cross correlation ( DCF) results for BL Lac. The time lag ![]() is in days.
is in days.
Figure 3:
Modelling the radio light curve with exponential flares for BL Lac. In the topmost panel is the optical light curve. In the lower panel are the individual model outbursts fitted to the radio light curve. The model light curve calculated from the individual model outbursts along with the radio light curve is plotted in the middle.
Figure 4:
Optical flux level vs. ![]() and flux of the model radio outbursts for BL Lac. At the epoch of each optical data point the phase and brightness of all the model radio outbursts and brightness of model light curve are calculated.
The results are calculated by averaging the optical flux in each of the ten intervals. The error bars indicate the standard error of the mean. The dots are connected for clarity.
and flux of the model radio outbursts for BL Lac. At the epoch of each optical data point the phase and brightness of all the model radio outbursts and brightness of model light curve are calculated.
The results are calculated by averaging the optical flux in each of the ten intervals. The error bars indicate the standard error of the mean. The dots are connected for clarity.
Figure 5:
The light curves for S2 0109+224.
Figure 6:
The DCF results for S2 0109+224.
Figure 7:
The TDF decomposition to individual outbursts for S2 0109+224 37 GHz light curve (see Fig. 3 for further explanation).
Figure 8:
Optical flux level vs. the phase ![]() and the flux level of individual outbursts and model light curve for S2 0109+224 (see Fig. 4 for further explanation).
and the flux level of individual outbursts and model light curve for S2 0109+224 (see Fig. 4 for further explanation).
Figure 9:
The light curves for PKS 0735+178.
Figure 10:
The DCF results for PKS 0735+178.
Figure 11:
Same as Fig. 7 for PKS 0735+178.
Figure 12:
Same as Fig. 8 for PKS 0735+178.
Figure 13:
The light curves for 1156+295 (4C 29.45).
Figure 14:
The DCF results for 1156+295 (4C 29.45).
Figure 15:
The light curves for 2251+158 (3C 454.3).
Figure 16:
The DCF results for 2251+158 (3C 454.3).
Figure 17:
Same as Fig. 7 for 2251+158 (3C 454.3).
Figure 18:
Same as Fig. 8 for 2251+158.