The procedure followed when determining a MOND rotation
curve has been described previously (e.g., BBS).
In the context of MOND, the true
gravitational acceleration g, is related to the Newtonian
acceleration ![]() as
as
| (1) |
| (2) |
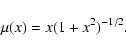 |
(3) |
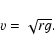 |
(4) |
| v4 = GMa0, | (5) |
The stellar disc may be assumed to be asymptotically thin or have a finite thickness related to the radial scale length of the disc by an empirical rule (van der Kruit & Searle 1981); this makes little difference in the final result. Applying Eqs. (1), (3), and (4), a least squares fit is then made to the observed rotation curve v(r) where the single free parameter of the fit is the mass-to-light ratio of the disc; in cases where there is an indication of a bulge from the light distribution, M/L of the bulge enters as a second parameter.
For the gaseous component a surface density distribution equal to that of the H I is taken, multiplied by a factor 1.3 to account for primordial helium. The gas layer is taken to be infinitesimally thin. The contribution of the gas to the total rotation is fixed, but does depend on the distance to the galaxy.
In principle, the parameter ![]() should be universal and, having
determined its magnitude, one is not allowed to adopt this as a free
parameter. But as noted above, the derived value of
should be universal and, having
determined its magnitude, one is not allowed to adopt this as a free
parameter. But as noted above, the derived value of ![]() does
depend upon the assumed distance scale. Sanders & Verheijen (1998)
give MOND fits to the rotation curves of 30 spiral galaxies in the
UMa cluster which they assume to be at 15.5 Mpc. The preferred
value of
does
depend upon the assumed distance scale. Sanders & Verheijen (1998)
give MOND fits to the rotation curves of 30 spiral galaxies in the
UMa cluster which they assume to be at 15.5 Mpc. The preferred
value of ![]() with this adopted distance is equal to the BBS value
of
with this adopted distance is equal to the BBS value
of
![]() cm s-2. However, based upon the Cepheid-based
re-calibrated Tully-Fisher relation (Sakai et al. 2000), Tully & Pierce
(2000) argue that the
distance to UMa should be taken to be 18.6 Mpc.
We have recalibrated the Tully-Fisher law using this same sample of galaxies
but with the three test galaxies (NGC 2403, NGC 3198, NGC 7331) left out
of the fitting. Within the errors, the slope and intercept of the
Tully-Fisher relation are the same as that found by Sakai et al. (2000),
and the distance to Ursa Major is only 1% smaller than that found
Tully & Pierce (2000). In that case the MOND fits to the UMa galaxies imply
that the value of
cm s-2. However, based upon the Cepheid-based
re-calibrated Tully-Fisher relation (Sakai et al. 2000), Tully & Pierce
(2000) argue that the
distance to UMa should be taken to be 18.6 Mpc.
We have recalibrated the Tully-Fisher law using this same sample of galaxies
but with the three test galaxies (NGC 2403, NGC 3198, NGC 7331) left out
of the fitting. Within the errors, the slope and intercept of the
Tully-Fisher relation are the same as that found by Sakai et al. (2000),
and the distance to Ursa Major is only 1% smaller than that found
Tully & Pierce (2000). In that case the MOND fits to the UMa galaxies imply
that the value of ![]() should be adjusted to
should be adjusted to
![]() cm s-2. This is also the
preferred value of
cm s-2. This is also the
preferred value of ![]() from MOND fits to rotation curves of a sample of
nearby dwarf galaxies with distances taken primarily from group membership
(Swaters & Sanders 2002, in preparation).
from MOND fits to rotation curves of a sample of
nearby dwarf galaxies with distances taken primarily from group membership
(Swaters & Sanders 2002, in preparation).
Copyright ESO 2002