Up: The Hernquist model revisited:
Subsections
6 Models with decreasing anisotropy
In order to construct dynamical models with a decreasing
anisotropy, i.e. with a tangentially anisotropic halo, no special
inversion techniques exist, such that we have to rely on the
general formulae of Dejonghe (1986) to invert the fundamental
integral Eq. (1). A disadvantage is that these
formulae are numerically unstable. Their usefulness is therefore
actually restricted to analytical models. But this is not
straightforward: a direct application of the inversion formulae to
an arbitrary analytical augmented density
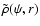 ,
even if its looks rather simple, can result in a cumbersome
mathematical exercise, because the inversion formulae are quite
elaborate.
,
even if its looks rather simple, can result in a cumbersome
mathematical exercise, because the inversion formulae are quite
elaborate.
A useful strategy to construct models with a tangential halo
without the need to cope with the complicated general formulae, is
to profit from the linearity of the integral
Eq. (1). In particular, it is very interesting to generate
augmented densities
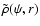 ,
which can be expanded
in a series of functions
,
which can be expanded
in a series of functions
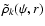 ,
which depend on
r only through a power law,
,
which depend on
r only through a power law,
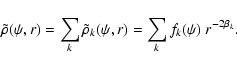 |
(64) |
Each of the augmented densities
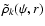 corresponds to a dynamical model with a constant anisotropy
corresponds to a dynamical model with a constant anisotropy
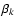 .
Combining the linearity of the integral
Eq. (1) with the results of Sect. 4.1, we
find that the distribution function corresponding to the density (64) reads 010
.
Combining the linearity of the integral
Eq. (1) with the results of Sect. 4.1, we
find that the distribution function corresponding to the density (64) reads 010
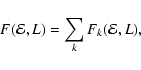 |
(65a) |
with
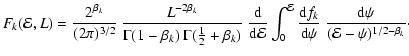 |
|
|
(65b) |
Equivalently, the moments of the distribution function can be
derived from the series expansion.
For every potential 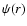 ,
we can create an infinite number of
functions
,
we can create an infinite number of
functions 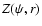 which satisfy the identity
which satisfy the identity
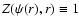 .
For the Hernquist potential, we can easily
create such a one-parameter family of functions
.
For the Hernquist potential, we can easily
create such a one-parameter family of functions
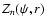 ,
,
![\begin{displaymath}Z_n(\psi,r)
=
\left[\psi~(1+r)\right]^n
\equiv
1,
\end{displaymath}](/articles/aa/full/2002/38/aa2799/img188.gif) |
(66) |
with n a natural number. If we multiply this family with the augmented
density (27) of the constant anisotropy
Hernquist models, we create a new two-parameter family of
dynamical models, that will self-consistently generate the
Hernquist potential-density pair,
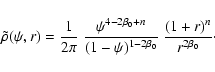 |
(67) |
Defining a new parameter
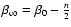 ,
we
can write this augmented density also as
,
we
can write this augmented density also as
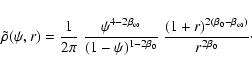 |
(68) |
Because we assumed that n is a natural number, we can expand the
binomial in the nominator of the density (67), and
write it in the form (64), with 010
with
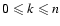 .
The reason why we chose
.
The reason why we chose 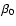 and
and
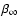 as parameters becomes clear when we look at the
expression for the anisotropy corresponding to this family of
density functions - for the moment being without bothering
whether the density corresponds to a physically acceptable
distribution function. By means of the formula (11),
we obtain
as parameters becomes clear when we look at the
expression for the anisotropy corresponding to this family of
density functions - for the moment being without bothering
whether the density corresponds to a physically acceptable
distribution function. By means of the formula (11),
we obtain
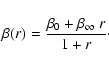 |
(70) |
The anisotropy equals 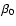 in the center and decreases to
in the center and decreases to
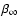 at large radii. Because n can in principle assume
any natural number, this family of augmented densities hence
corresponds to dynamical models which can grow arbitrarily
tangential in the outer regions. In particular, by setting n=0we recover the models with constant anisotropy
at large radii. Because n can in principle assume
any natural number, this family of augmented densities hence
corresponds to dynamical models which can grow arbitrarily
tangential in the outer regions. In particular, by setting n=0we recover the models with constant anisotropy
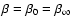 from Sect. 4.2.
from Sect. 4.2.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{MS2799f6.eps}\end{figure}](/articles/aa/full/2002/38/aa2799/Timg200.gif) |
Figure 6:
Comparison of the distribution function corresponding to
Hernquist model with increasing anisotropy with
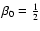 and
and
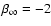 ,
and the constant
anisotropy model with ,
and the constant
anisotropy model with 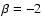 .
The distribution functions are
represented as isoprobability contours in turning point space. .
The distribution functions are
represented as isoprobability contours in turning point space. |
We can calculate the distribution function of these models by
applying the recipe (65b) to each of the components (69ab).
We obtain after some algebra
This family of models is restricted by the condition
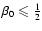 ,
because for higher values of
,
because for higher values of 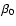 the distribution function becomes negative. For all half-integer
and integer values of
the distribution function becomes negative. For all half-integer
and integer values of 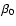 (and therefore also of
(and therefore also of
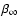 ), this expression can be written in terms of
elementary functions, very analogous with the distribution
functions of the constant anisotropy models: the expression
contains integer and half-integer powers of
), this expression can be written in terms of
elementary functions, very analogous with the distribution
functions of the constant anisotropy models: the expression
contains integer and half-integer powers of 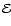 and
and
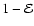 and a factor
and a factor
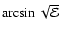 .
The models
characterized by
.
The models
characterized by
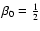 are of a particular kind.
The hypergeometric functions in Eq. (71) disappears
for
are of a particular kind.
The hypergeometric functions in Eq. (71) disappears
for
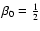 ,
such that the distribution function
can be written as a finite power series of
,
such that the distribution function
can be written as a finite power series of
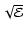 and L.
and L.
An interesting characteristic of these models is revealed when we
look at the asymptotic behavior of the distribution function at
large radii, i.e. for
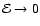 .
The term
corresponding to k=n will contribute the dominant term in the
sum (71), such that we obtain
.
The term
corresponding to k=n will contribute the dominant term in the
sum (71), such that we obtain
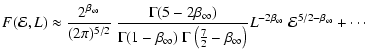 |
|
|
(72) |
This expansion is at first order independent of 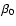 ,
such
that all models with the same
,
such
that all models with the same
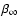 will have a similar
behavior at large radii. In particular, all distribution functions
corresponding to a particular
will have a similar
behavior at large radii. In particular, all distribution functions
corresponding to a particular
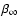 will at large radii
behave as the Hernquist model with constant anisotropy
will at large radii
behave as the Hernquist model with constant anisotropy
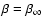 .
This is illustrated in Fig. 6, where we compare the distribution function of
a model with a radial core and a tangential halo with the constant
anisotropy model that has the corresponding tangential anisotropy.
At small radii, the difference between both distribution functions
is obvious: the former one has more stars on radial orbits,
whereas the latter prefers to populate circular-like orbits. At
large radii, however, the isoprobability contours of both models
agree very well.
.
This is illustrated in Fig. 6, where we compare the distribution function of
a model with a radial core and a tangential halo with the constant
anisotropy model that has the corresponding tangential anisotropy.
At small radii, the difference between both distribution functions
is obvious: the former one has more stars on radial orbits,
whereas the latter prefers to populate circular-like orbits. At
large radii, however, the isoprobability contours of both models
agree very well.
Finally, notice that there is no analogue for this behavior at
small radii: not all models with a fixed 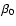 will have a
similar behavior for
will have a
similar behavior for
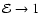 ,
i.e. at small
radii.
,
i.e. at small
radii.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{MS2799f7.eps}\end{figure}](/articles/aa/full/2002/38/aa2799/Timg210.gif) |
Figure 7:
The radial (upper panel) and line-of-sight (lower panel)
velocity dispersion profiles of Hernquist models with a decreasing
anisotropy. All models have the same tangential outer anisotropy
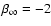 ,
but they have a different central anisotropy
parameter ,
but they have a different central anisotropy
parameter 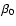 :
plotted are :
plotted are
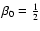 ,
0, ,
0,
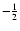 ,
-1 and -2 (black line). ,
-1 and -2 (black line). |
In order to calculate the velocity dispersion profiles of the
models of this type, we have various possibilities. We can either
calculate the dispersion for each of the n terms (69a)
through formula (26) and sum the
results, or directly apply the general recipe (8ab)
on the expression (68). In either case, we obtain an
expression very akin to the expression (32) of the
models with constant anisotropy,
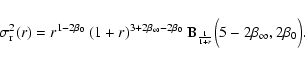 |
(73) |
This expression can be written in terms of elementary functions
for all 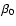 with
with 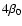 an integer (and hence also
an integer (and hence also
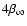 an integer).
an integer).
Not as a surprise, the asymptotic expressions for
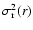 for
for 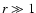 read
read
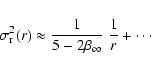 |
(74) |
i.e. they are similar to the corresponding expansions of the
constant anisotropy models with
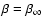 .
This
behavior is illustrated in the upper panel of Fig. 7,
where we plot the radial velocity dispersion
profile for a set of models with varying
.
This
behavior is illustrated in the upper panel of Fig. 7,
where we plot the radial velocity dispersion
profile for a set of models with varying 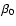 and a fixed
and a fixed
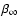 .
At small radii, the models have different profiles
(those with the most radial anisotropy have the largest values of
.
At small radii, the models have different profiles
(those with the most radial anisotropy have the largest values of
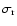 ), but at large radii, they all converge towards a
common asymptotic expansion.
), but at large radii, they all converge towards a
common asymptotic expansion.
The calculation of the line-of-sight velocity dispersion is also
similar to the case of constant anisotropy. It is found that
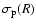 can be written in terms of elementary functions for
all integer and half-integer values of
can be written in terms of elementary functions for
all integer and half-integer values of 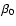 ,
and that the
asymptotic behavior for
,
and that the
asymptotic behavior for 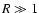 reads
reads
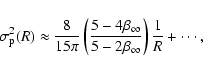 |
(75) |
which is at first order independent of 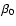 .
An illustration
is shown in the bottom panel of Fig. 7.
.
An illustration
is shown in the bottom panel of Fig. 7.


Up: The Hernquist model revisited:
Copyright ESO 2002
![]() ,
even if its looks rather simple, can result in a cumbersome
mathematical exercise, because the inversion formulae are quite
elaborate.
,
even if its looks rather simple, can result in a cumbersome
mathematical exercise, because the inversion formulae are quite
elaborate.
![]() ,
which can be expanded
in a series of functions
,
which can be expanded
in a series of functions
![]() ,
which depend on
r only through a power law,
,
which depend on
r only through a power law,
![]() ,
we can create an infinite number of
functions
,
we can create an infinite number of
functions ![]() which satisfy the identity
which satisfy the identity
![]() .
For the Hernquist potential, we can easily
create such a one-parameter family of functions
.
For the Hernquist potential, we can easily
create such a one-parameter family of functions
![]() ,
,
![\begin{displaymath}Z_n(\psi,r)
=
\left[\psi~(1+r)\right]^n
\equiv
1,
\end{displaymath}](/articles/aa/full/2002/38/aa2799/img188.gif)
![]() .
The reason why we chose
.
The reason why we chose ![]() and
and
![]() as parameters becomes clear when we look at the
expression for the anisotropy corresponding to this family of
density functions - for the moment being without bothering
whether the density corresponds to a physically acceptable
distribution function. By means of the formula (11),
we obtain
as parameters becomes clear when we look at the
expression for the anisotropy corresponding to this family of
density functions - for the moment being without bothering
whether the density corresponds to a physically acceptable
distribution function. By means of the formula (11),
we obtain
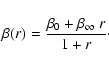
![]() .
The term
corresponding to k=n will contribute the dominant term in the
sum (71), such that we obtain
.
The term
corresponding to k=n will contribute the dominant term in the
sum (71), such that we obtain
![]() will have a
similar behavior for
will have a
similar behavior for
![]() ,
i.e. at small
radii.
,
i.e. at small
radii.
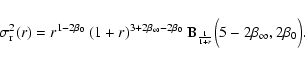
![]() for
for ![]() read
read
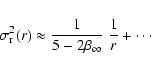
![]() can be written in terms of elementary functions for
all integer and half-integer values of
can be written in terms of elementary functions for
all integer and half-integer values of ![]() ,
and that the
asymptotic behavior for
,
and that the
asymptotic behavior for ![]() reads
reads