

Up: The Hernquist model revisited:
Subsections
4.1 Background
A special family of distribution functions that can easily be
generated using the technique outlined in Sect. 2 corresponds to
models with a density that depends on r only through a factor
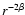 ,
i.e.
,
i.e.
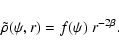 |
(22) |
It is well known that such densities correspond to models with a
constant anisotropy (i.e. Binney & Tremaine 1987), which can
easily be checked by introducing
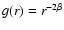 in the formula
(11). For a given potential-density pair, a family
of models with constant anisotropy can hence be constructed by
inverting the potential as
in the formula
(11). For a given potential-density pair, a family
of models with constant anisotropy can hence be constructed by
inverting the potential as 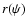 ,
and defining
,
and defining
 |
(23) |
Notice that such models are not the only constant anisotropy
models corresponding to a given potential-density pair, as argued in
Sect. 1.5 of Dejonghe (1986). This family, however, is very
attractive due to its relative simpleness. In particular, the
corresponding distribution function is a power law in L, and can
be found through an Eddington-like formula,
 |
|
|
(24) |
For the moments of the distribution function, the relation (7)
can be simplified to
 |
|
|
(25) |
In particular, the radial velocity dispersions reads
 |
(26) |
4.2 Hernquist models with a constant anisotropy
4.2.1 The distribution function
![\begin{figure}
\par\includegraphics[width=13.4cm,clip]{MS2799f1.eps}\end{figure}](/articles/aa/full/2002/38/aa2799/Timg81.gif) |
Figure 1:
The distribution function of the Hernquist models with a
constant anisotropy, represented as isoprobability contours in
turning point space. The distribution functions in solid lines
represent a radial model with
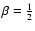 (left panel)
and a tangential model with
(left panel)
and a tangential model with 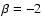 (right panel). The dotted
contour lines in both panels correspond to the isotropic Hernquist
model.
(right panel). The dotted
contour lines in both panels correspond to the isotropic Hernquist
model. |
Applying the formula (23) to the Hernquist
potential-density pair (2ab) yields
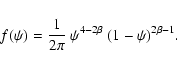 |
(27) |
Substituting this expression into the general formula (24)
gives us the corresponding distribution function
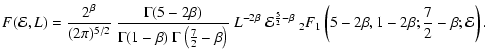 |
|
|
(28) |
This expression reduces to the isotropic distribution function (17) for 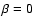 ,
as required. Whether the expression (28) corresponds to a physically acceptable
distribution function for a given value of
,
as required. Whether the expression (28) corresponds to a physically acceptable
distribution function for a given value of 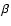 depends on the
condition that the distribution function has to be positive over
the entire phase space.
depends on the
condition that the distribution function has to be positive over
the entire phase space.
It is no surprise that the distribution function is not positive
for the largest possible values of 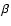 ,
because models where
only the radial orbits are populated can only be supported by a
density profile that diverges as r-2 or steeper in the center
(Richstone & Tremaine 1984). It turns out that the distribution
function (28) is everywhere non-negative for
,
because models where
only the radial orbits are populated can only be supported by a
density profile that diverges as r-2 or steeper in the center
(Richstone & Tremaine 1984). It turns out that the distribution
function (28) is everywhere non-negative for
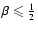 .
.
For all integer and half-integer values of 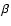 ,
the
hypergeometric series in (28) can be expressed in terms
of elementary functions. Very useful are half-integer values of
,
the
hypergeometric series in (28) can be expressed in terms
of elementary functions. Very useful are half-integer values of
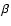 ,
because the energy-dependent part of the distribution
function can then be written as a rational function of
,
because the energy-dependent part of the distribution
function can then be written as a rational function of
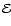 .
For integer values of
.
For integer values of 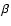 ,
the hypergeometric
series can be written as a function containing integer and
half-integer powers of
,
the hypergeometric
series can be written as a function containing integer and
half-integer powers of 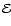 and
and
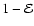 and a factor
and a factor
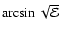 ,
similar to the isotropic distribution
function (17).
,
similar to the isotropic distribution
function (17).
The limiting model
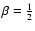 is particularly simple. It
has an augmented density that is a power law of potential and
radius,
is particularly simple. It
has an augmented density that is a power law of potential and
radius,
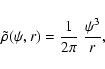 |
(29) |
and the corresponding distribution function simply reads
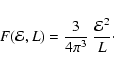 |
(30) |
This model is a special case of the generalized polytropes discussed
by Fricke (1951) and Hénon (1973).
In Fig. 1 we compare the distribution functions
of the radial model with
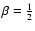 and the tangential
model with
and the tangential
model with 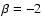 with the distribution function of the
isotropic Hernquist model. The distribution functions are shown by
means of their isoprobability contours in turning point space,
which can easily be interpreted in terms of orbits. Compared to
the isotropic model, the radial model prefers orbits on the upper
left side of the diagram, with an apocenter much larger than the
pericenter, i.e. elongated orbits. The isoprobability contours of
tangential models on the other hand lean towards the diagonal axes
where pericenter and apocenter are equal, i.e. nearly-circular
orbits are preferred.
with the distribution function of the
isotropic Hernquist model. The distribution functions are shown by
means of their isoprobability contours in turning point space,
which can easily be interpreted in terms of orbits. Compared to
the isotropic model, the radial model prefers orbits on the upper
left side of the diagram, with an apocenter much larger than the
pericenter, i.e. elongated orbits. The isoprobability contours of
tangential models on the other hand lean towards the diagonal axes
where pericenter and apocenter are equal, i.e. nearly-circular
orbits are preferred.
By means of substituting the expression (27) into the
general formula (7), we can derive an analytical
expression for all moments of the distribution function,
We are mainly interested in the velocity dispersions, which can be
conveniently written by means of the incomplete Beta function
(Abramowitz & Stegun 1972),
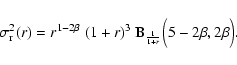 |
(32) |
For all anisotropies
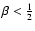 ,
the radial dispersion
equals zero in the center of the galaxy, rises until a maximum and
then decreases again towards zero for
,
the radial dispersion
equals zero in the center of the galaxy, rises until a maximum and
then decreases again towards zero for
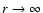 .
The
asymptotic behavior for
.
The
asymptotic behavior for 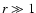 is
is
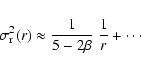 |
(33) |
The expression (32) can be written in terms of
elementary functions for all 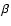 with
with 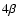 an integer. For
the integer and half-integer values of
an integer. For
the integer and half-integer values of 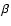 ,
the expression
involves polynomials in r and a factor
,
the expression
involves polynomials in r and a factor
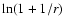 ,
very
analogous to the expression (19) of the isotropic
Hernquist model. For the quarter-integer values of
,
very
analogous to the expression (19) of the isotropic
Hernquist model. For the quarter-integer values of 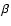 ,
it
contains polynomials and square roots in r and a factor
,
it
contains polynomials and square roots in r and a factor
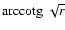 .
.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{MS2799f2.eps}\end{figure}](/articles/aa/full/2002/38/aa2799/Timg105.gif) |
Figure 2:
The velocity dispersion of the Hernquist models with a
constant anisotropy. The upper and lower panels show the radial
velocity dispersions
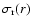 and the line-of-sight velocity
dispersion
and the line-of-sight velocity
dispersion
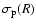 .
The profiles are shown for different
values of the anisotropy parameter .
The profiles are shown for different
values of the anisotropy parameter 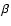 :
plotted are :
plotted are
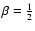 , ,
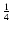 ,
0, ,
0,
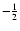 ,
-2,
-5 and the limit case ,
-2,
-5 and the limit case
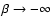 . . |
Particular cases are the models that correspond to the most radial
and tangential distribution functions. On the one hand, the limit
case
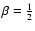 has the simple velocity dispersion
profiles
has the simple velocity dispersion
profiles
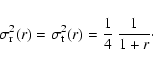 |
(34) |
Particular about this dispersion profile is that it assumes a
finite value in the center. On the other side of the range for
possible anisotropies, we can consider the limit
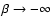 ,
which corresponds to a model with
purely circular orbits. For such a model, the radial dispersion is
of course identically zero, whereas the transverse velocity
dispersion is the circular velocity corresponding to the Hernquist
potential,
,
which corresponds to a model with
purely circular orbits. For such a model, the radial dispersion is
of course identically zero, whereas the transverse velocity
dispersion is the circular velocity corresponding to the Hernquist
potential,
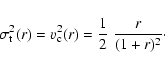 |
(35) |
In the top panel of Fig. 2 we plot the radial
velocity dispersion profile for various models with a different
anisotropy 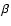 .
Both at small and large radii, the radial
dispersion is a decreasing function of
.
Both at small and large radii, the radial
dispersion is a decreasing function of 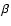 ,
as expected.
,
as expected.
The line-of-sight velocity dispersion for anisotropic models is
found through the formula
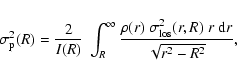 |
(36) |
where
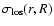 is the velocity dispersion at the
position r on the line of sight R in the direction of
observer. It is a linear combination of the radial and transverse
velocity dispersions in this point,
is the velocity dispersion at the
position r on the line of sight R in the direction of
observer. It is a linear combination of the radial and transverse
velocity dispersions in this point,
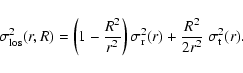 |
(37) |
We can equivalently write
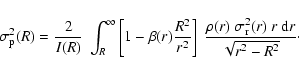 |
(38) |
For the general Hernquist models with a constant anisotropy, the
integration (38) cannot be performed analytically. But
for all integer and half-integer 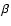 's,
's,
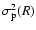 can be
expressed in terms of polynomials and the function X, defined in
Eq. (4). For example, for the limit model
can be
expressed in terms of polynomials and the function X, defined in
Eq. (4). For example, for the limit model
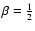 we obtain after some algebra
we obtain after some algebra
For the other limit model, the one with only circular orbits, we
find
in agreement with Hernquist (1990).
In the bottom panel of Fig. 2 we plot the
line-of-sight dispersion profiles for a number of different values
of 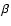 .
The behavior of the individual profiles is analogous
to the spatial dispersion profiles: except for the
.
The behavior of the individual profiles is analogous
to the spatial dispersion profiles: except for the
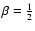 model, which has a finite central dispersion,
the
model, which has a finite central dispersion,
the
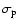 profiles start at zero in the center, rise strongly
until a certain maximum and then decrease smoothly towards zero at
large projected radii. The behavior for
profiles start at zero in the center, rise strongly
until a certain maximum and then decrease smoothly towards zero at
large projected radii. The behavior for 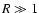 can be quantified
if we introduce the asymptotic expansion (33) into the
formula (38),
can be quantified
if we introduce the asymptotic expansion (33) into the
formula (38),
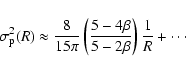 |
(41) |
The dependence of the line-of-sight dispersion as a function of
the anisotropy is depends strongly on the projected radius: at
small projected radii,
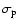 decreases with increasing
decreases with increasing
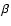 ,
whereas for large radii,
,
whereas for large radii,
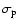 increases with
increasing
increases with
increasing 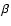 .
In other words, radial models have a larger
central and a smaller outer line-of-sight dispersion than their
tangential counterparts. This is a direct consequence of the
weight of the radial and transversal velocity dispersions in the
linear combination (37): at small projected radii, the
radial dispersion contributes the dominant term, whereas for the
outer lines of sight, the transversal dispersion term dominates.
.
In other words, radial models have a larger
central and a smaller outer line-of-sight dispersion than their
tangential counterparts. This is a direct consequence of the
weight of the radial and transversal velocity dispersions in the
linear combination (37): at small projected radii, the
radial dispersion contributes the dominant term, whereas for the
outer lines of sight, the transversal dispersion term dominates.


Up: The Hernquist model revisited:
Copyright ESO 2002
![]() ,
i.e.
,
i.e. 
![]() ,
because models where
only the radial orbits are populated can only be supported by a
density profile that diverges as r-2 or steeper in the center
(Richstone & Tremaine 1984). It turns out that the distribution
function (28) is everywhere non-negative for
,
because models where
only the radial orbits are populated can only be supported by a
density profile that diverges as r-2 or steeper in the center
(Richstone & Tremaine 1984). It turns out that the distribution
function (28) is everywhere non-negative for
![]() .
.
![]() ,
the
hypergeometric series in (28) can be expressed in terms
of elementary functions. Very useful are half-integer values of
,
the
hypergeometric series in (28) can be expressed in terms
of elementary functions. Very useful are half-integer values of
![]() ,
because the energy-dependent part of the distribution
function can then be written as a rational function of
,
because the energy-dependent part of the distribution
function can then be written as a rational function of
![]() .
For integer values of
.
For integer values of ![]() ,
the hypergeometric
series can be written as a function containing integer and
half-integer powers of
,
the hypergeometric
series can be written as a function containing integer and
half-integer powers of ![]() and
and
![]() and a factor
and a factor
![]() ,
similar to the isotropic distribution
function (17).
,
similar to the isotropic distribution
function (17).
![]() is particularly simple. It
has an augmented density that is a power law of potential and
radius,
is particularly simple. It
has an augmented density that is a power law of potential and
radius,
![]() and the tangential
model with
and the tangential
model with ![]() with the distribution function of the
isotropic Hernquist model. The distribution functions are shown by
means of their isoprobability contours in turning point space,
which can easily be interpreted in terms of orbits. Compared to
the isotropic model, the radial model prefers orbits on the upper
left side of the diagram, with an apocenter much larger than the
pericenter, i.e. elongated orbits. The isoprobability contours of
tangential models on the other hand lean towards the diagonal axes
where pericenter and apocenter are equal, i.e. nearly-circular
orbits are preferred.
with the distribution function of the
isotropic Hernquist model. The distribution functions are shown by
means of their isoprobability contours in turning point space,
which can easily be interpreted in terms of orbits. Compared to
the isotropic model, the radial model prefers orbits on the upper
left side of the diagram, with an apocenter much larger than the
pericenter, i.e. elongated orbits. The isoprobability contours of
tangential models on the other hand lean towards the diagonal axes
where pericenter and apocenter are equal, i.e. nearly-circular
orbits are preferred.
![]() has the simple velocity dispersion
profiles
has the simple velocity dispersion
profiles
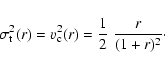
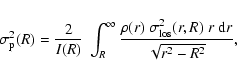
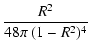
![]() .
The behavior of the individual profiles is analogous
to the spatial dispersion profiles: except for the
.
The behavior of the individual profiles is analogous
to the spatial dispersion profiles: except for the
![]() model, which has a finite central dispersion,
the
model, which has a finite central dispersion,
the
![]() profiles start at zero in the center, rise strongly
until a certain maximum and then decrease smoothly towards zero at
large projected radii. The behavior for
profiles start at zero in the center, rise strongly
until a certain maximum and then decrease smoothly towards zero at
large projected radii. The behavior for ![]() can be quantified
if we introduce the asymptotic expansion (33) into the
formula (38),
can be quantified
if we introduce the asymptotic expansion (33) into the
formula (38),